积累活动经验 理解知识本质
2016-05-14孙艳君
孙艳君


长期以来,计算规则图形的面积已经达成共识. 但是现实生活中存在很多图形,分割后仍难以找到基本的图形,需要学生有较强的估计能力,会用各种方法相对准确地得到它的面积. 在以前的教材中,并没有安排不规则图形的面积问题. 因此北师版教材把这一内容编入教材,要求学生掌握估计、计算不规则图形的面积,这不仅有助于培养学生的空间观念,同时也有助于提高学生解决问题的能力. 《成长的脚印》就是这一领域的一个内容.
一、对学习内容的分析
(一)学科本质分析
关于不规则图形的面积怎么求?吴正宪老师是这样说的:首先要确定单位,也就是把图形放到格子里去数去估. 其次就是要想清楚怎么去估?既然是去估测,就不是去找一个点,应该找上限、下限,确定取值范围. 关于估计,《义务教育数学课程标准》是这样要求的:学段一:会选择合适的单位去估计;学段二:会选择合适的方法去估计. 估就是换一个思想解决问题,在生活中估比精更重要.
(二)教材分析
本节课教材原有的设计大部分是值得借鉴的,但经过对课标的解读,专家的讲座的分析和对多个不同版本教材的对比之后,我们对教材进行了个性化处理.
首先,教材直接给出格子图中的脚印,没有让学生体会到格子图也就是确定测量单位的必要性. 而确定单位是求不规则图形面积的重要一步,教材这样直接给出是不合理的. 鉴于此,我们首先给出的脚印是不带格子的,在引导学生复习规则图形面积的基础上,让学生知道求一个图形的面积其实就是求这个图形所包含的面积单位的个数,从而让学生深刻地体会到要知道不规则图形的面积也是求它所包含的面积单位的个数,也就是格子的数量.
其次,教材给出的两个不同脚印面积的测量,用的格子都是1平方厘米,这样不利于学生体会测量单位越小测量的结果越精准. 在让学生用数格子的方法,估计不规则图形的面积的同时,向学生提供大小不同的格子,这不仅可以丰富学生估计的策略和方法,更为关键的是可以让学生体会到格子越小得到的面积越接近实际面积.
二、对学生认知的分析
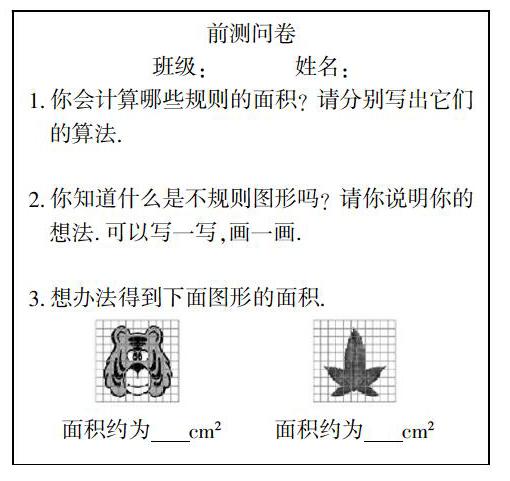
在上课之前,为了确定学生对本节课的学习是否已经有了良好的认知基础和数学活动经验,是否已经部分或全部掌握了本节课的知识内容,我进行了问卷调查.
前测试题共包括两个部分:第一部分是本节课的知识基础,即规则图形的面积及面积计算方法,即问卷的第一题. 如果学生已有的认知基础或数学活动经验比较薄弱,那么在课初我就应该想办法帮助学生补救经验,理清思路. 如果学生的认知方式非常成熟,已有的知识基础扎实,那么在课初就可以一语带过. 第二部分是本节课的新知,即不规则图形的面积的定义及如何得到不规则图形的面积,即问卷的第二题和第三题. 如果学生对本节课的新知觉得困难无以应对,那么这节课应该降低难度,减缓坡度,分解目标,让学生可以拾级而上. 如果学生对新知已经基本了解,并有一定的想法,那么这节课就可以提高难度,整合目标,让学生获得更大的发展和提升.
全班共40人,全部参与前测,获有效问卷40份,现分析如下:
1. 学生的认知基础分析
第一题:“你会计算哪些规则图形的面积?请分别写出它们的算法. ”这是本节课的知识基础部分,调查结果显示40人全部做答并完全正确,个别同学没有把学过的所有规则图形的面积进行做答,但是只要做答的都完全正确. 这表明全班学生对于规则图形的面积及面积计算方法都掌握的很扎实.
2. 学生对新知的理解情况分析
第二题:“你知道什么是不规则图形吗?请说明你的想法,可以写一写,画一画. ”该题主要是通过对学生的表征方式的分析与考察,来了解学生对新知的理解程度.
调查结果显示:很多学生对能够利用不同的表征方式去理解不规则图形. 这说明学生对不规则图形的内涵或外延有了很好的理解.
调查结果显示:大多数学生对不规则图形有一定的认识,也有少部分同学出现了概念混淆,产生了错误的理解. 接下来的教学有必要对不规则图形的定义进行界定.
3. 学生对新知的掌握情况分析
第三题:“请你想办法得到下面不规则图形的面积. ”该题主要是通过对学生的已经掌握的方法的分析与考察,来了解学生对新知的掌握程度.
调查结果显示:大多数学生对于一一拼凑数格子和转化的方法有了很好的经验,而半格法和大于半格记为1格,小于半格记为0格,是绝大多数学生所不知道的,这就应该是本节课在数格的方法策略研究的重点.
大多数学生对于得到答案本身没有问题,因此通过不同方法策略的对比,引导学生得到一个相对合理的范围,才是这节课的关键.
三、教学设计与意图
本节课在前面的分析和思考的基础上,形成以下设计:
(一)以求规则图形的面积为基础,认识不规则图形及其面积的求法
师:同学们,这节课我们一起来学习有关面积的知识. 这些都是我们学过的由直线段围成的什么图形?它们的面积都是怎么算的?长方形的面积公式是什么?那长乘宽其实求的是什么?对了,是它所包含的面积单位的个数.
师:其实所有这节规则图形都是用公式很快地得到它多包含的面积单位的个数,也就是它的面积. 谁还记得面积单位都是怎么规定的了?都是以一定边长的正方形的面积为标准. 师:其实生活中很多事物的形状并不都是这样规则的,它是由曲线围成的不规则图形. 什么啊?猜猜看!野人的脚印. 有什么好办法能得到这个脚印的面积呢?那你能直接计算出它们的面积吗?我们要想知道它的面积究竟有多大,其实只需要知道它到底包含几个面积单位?要数的这些格子其实就是一个一个的面积单位,通过数格子我们就可以知道这个不规则的图形所包含的面积单位的个数.
通过复习规则图形的面积,让学生知道所有规则图形的面积其实都是用公式很快地得到它多包含的面积单位的个数. 通过复习对面积单位的规定,让学生知道不同的面积单位其实都是以一定边长的正方形的面积的大小为标准. 在引导学生复习规则图形面积的基础上,让学生知道求一个图形的面积其实就是求这个图形所包含的面积单位的个数,从而让学生深刻地体会到要知道不规则图形的面积也是求它所包含的面积单位的个数,也就是格子的数量.
(二)通过不同方法的比较,掌握拼凑和转化两种策略
1. 数估大格
(1)拼凑
师:他是怎么数的?也就是说他在数之前先对格子进行了分类,整格和不足一格. 老师想问问你在数的时候,什么样的格子不好数?这不好数的你是用什么方法数的?
(2)转化
割补画长方形
师:他这是什么方法?把不规则的脚印转化为规则的长方形. (板书:不规则 规则)我们都一个一个再数,你能算出来. 他把外面多的部分移给里面少的,其实也是在拼凑. 只不过刚才凑的是整格,现在凑的是长方形.
在外面画长方形
师:你真厉害!我们都一直瞪着脚印在数,你没数也没凑,直接在脚印外面圈了一个长方形. 行不行?为什么不行?他得到的面积比脚印的面积大了. 有没有优点?可以很快地算出来,不用一个格一个格去数了. 如果我们对结果的精准度没有那么高要求的时候,他这个是完全可以的.
2. 数估小格
师:看来,要想相对准确地得到脚印的面积,无论大格小格把不足一格拼凑成整格确实是一个好办法!但是这个不足一格的和大格子比起来多多了,一个一个拼凑起来你们觉得怎么样?有没有不是一一拼凑,但也数出来的?
(1)拼凑
方法一:(板书:大于半格:1,小于半格:0)
师:少半格的都没数,还准吗?
方法二:(板书:÷2)
师:他把所有不足一格都加起来再除以2,相当于他把所有不足一格的都看成多大了?对了,半格. 然后再两两拼凑成整格. 数小格的有没有用不一样的方法了?
(2)转化
方法一:大长方形、不足一格都看成一格
师:这回我们可以确定脚印的实际面积一定小于多少了?刚才我们确定脚印面积一定比那个小,现在又有这个小了?怎么回事?刚才大格子圈的旁边空的地方大,现在小格子圈的空的地方小了,所以就更接近了,范围也就小了.
方法二:小长方形、不足一格都不看
师:通过他的方法我们知道了脚印的面积一定比这个小,那脚印的面积一定比多大大呢?有没有同学得到结论的?你看老师这样画行不行?(师用彩笔画长方形)脚印的面积是不是一定比它大呢?
师:虽然我们没有得到脚印的实际面积到底有多大,经过大家的努力,我们确定了一个范围,如果你数得的结果在这个范围内就更合理了.
根据学生的知识水平教给学生一些基本的估计方法,通过估数大格、小格不同方法的比较,使学生掌握拼凑和转化两种策略.
(三)通过大格和小格的对比,体会单位越小测量的结果越准
师:看看左边的答案是我们数大格得到的,右边的答案是数小格得到的. 你想说点什么?老师现在想问一下你们都谁数的大格?谁数的小格?都说说你为什么选它?
师:你们的直觉是小格子准,观察这些数据的结果也是小格子的答案比较集中,好像挺准的,那小格子准的道理是什么呢?有道理,看来确实是格子越小数得的面积就越接近脚印的实际面积. 那如果格子再小呢?再小呢?那我还想再接近实际面积,怎么办?
所有的格子平均分成4份,分成更小的格子,再平均分成4份,分成更小的格子,我们还以重新设定更小的格子为单位,这样不断地去逼近,这个时候探索出更逼近实际的那个准确值. 通过调查学生刚开始选卡的原因,知道学生的直觉是格子越小越准. 经过后来讨论和大小格子的数据的对比,让学生明白格子越小越准的道理.
(四)积累活动经验,沟通知识联系,突出面积及测量本质
1. 沟通不规则图形与规则图形的联系,理解求面积的通法通则
师总结:同学们,我们一起学习了不规则图形的面积,其实无论是规则的图形还是不规则的图形,我们知道要想知道它的面积究竟有多大,其实就是要测量或计算出它所包含的面积单位的个数.
数方格测量所有图形面积的通性通法. 无论是规则的图形还是不规则的图形,我们知道要想知道它的面积究竟有多大,其实就是要测量或计算出它所包含的面积单位的个数.
2. 沟通测量面积与长度、体积的相通之处,突出测量的本质
师:提到测量,大家一定不陌生. 从一年级到现在,其实我们已经学习了很多测量的知识,比如测量长度,测量面积,还有即将学习的立体图形的测量. 其实它们的道理都是一样的,就根据实际的需要选择合适的单位去量,要想保证测量结果的精准,就要选择足够小的单位.
由对二维面积的测量,沟通学生学过的一维长度的测量,后面即将学习三维体积的测量的联系,突出测量的本质就是测量长度、面积、体积所包含的单位的个数. 根据实际的需要选择合适的单位去量,要想保证测量结果的精准,就要选择足够小的单位.
四、教学效果与反思
(一)积累经验,促进学生思维发展
本节课学生完整经历了这样一个发现问题,提出问题,勇敢地去尝试解决问题的过程. 这才是积极意义上的探索者,而不是亦步亦趋地跟着老师的伪探索,充其量是个操作工. 学生可能不懂什么是逼近,但是在这个过程中它体会着极限思想,在活动中积累着活动经验. 它今后遇到问题还能去等吗?他一定是积极地去思考,去解决.
(二)尊重差异,促进个性发展
本节课我设计了两种不同的独立学习卡供学生选择,分别是4平方厘米的大格和1平方厘米的小格. 性子急的学生追求速度,会选择大格子的,思维严谨的学生追求精准,会选择小格子的. 尊重差异,开发不同的学习资源,更有利于促进学生的个性发展.
(三)保护天性,促进自主发展
本节课我试图充分保护学生的天性. 具体表现在:1.创设有价值的情境,保护学生爱探究的天性. 2.保护学生爱问的天性. 3.保护学生爱表达的天性. 教师不用担心讲不完,不要担心学生说不明白,要相信学生,下一名学生要表达的很可能正是你着急要说的. 长此以往,学生会越来越爱探究,越来越爱表达,结果是越来越喜欢数学课.
