几何证明推理入门

雷霞

几何证明是培养学生逻辑思维的起步，是学生对几何图形从感性认识到理性认识的升华。几何证明题的推理过程，对几何证明入门者来讲是一大难题。那么，如何才能顺利写出几何证明题的推理过程呢？

一、熟记文字语言、符号语言、图形语言间的相互关系

几何证明题，体现的是文字语言、符号语言、图形语言三种语言之间的相互转化与应用。在学习几何图形的有关概念、公理、定理、性质、判定等时，不仅要理解命题中文字语言所蕴含的本质，还要熟记命题对应的符号语言和图形语言。只有将三者紧密结合，才能对几何图形的有关概念、公理、定理、性质、判定等灵活运用，进而比较顺利地写出几何证明题的推理过程。

例1：学习平行线的判定方法1：两条直线被第三条直线所截，如果同位角相等，那么这两条直线平行。（简单说成：同位角相等，两直线平行。）我们要明确其三种语言及其本质和作用：

二、关注图形已知

有一类知识点，依托图形出现，只要有图就有其身影存在，这类知识我们可以理解为图形已知，在几何证明的推理过程中可以直接应用。例2：

三、学会“走一走，看一看”

在几何证明中常用的方法是演绎推理，演绎推理指的是从已知条件出发，根据已经学过的数学概念、公理、定理、性质等知识，顺着推理，由“已知”得“推知”，由“推知”得“未知”，逐步推出求证的结论的方法。在具体的证明推理中，我们要学会“走一走，看一看”。所谓“走一走”，就是从“已知”条件出发“走一走”，得“推知”；而“看一看”，则是结合“推知”看“结论”，结合“推知”“结论”看图形。这样，“边走边看”就可以顺利写出推理过程，进而推出求证的结论。

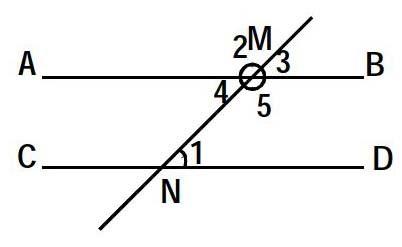
例3：如图，已知AB∥CD，EF分别交AB、CD于M、N。

■

求证：∠1+∠2=180°。

分析一：从“已知”条件出发“走一走”

由已知AB∥CD，可推知∠1=∠3①；

结合“推知”看“结论”：推知引出∠3，结论含有∠2；

结合“推知”“结论”看图形：图中有∠2+∠3=180°②；

由①②即可推出求证的结论∠1+∠2=180°。

分析二：从“已知”条件出发“走一走”

由已知AB∥CD，可推知∠1=∠4③；

结合“推知”看“结论”：推知引出∠4，结论含有∠2；

结合“推知”“结论”看图形：图中有∠2+∠4=180°④；

由③④即可推出求证的结论∠1+∠2=180°。

分析三：从“已知”条件出发“走一走”

由已知AB∥CD，可推知∠1+∠5=180°⑤；

结合“推知”看“结论”：推知引出∠5，结论含有∠2；

结合“推知”“结论”看图形：图中有∠2=∠5⑥；

由⑤⑥即可推出求证的结论∠1+∠2=180°。

总之，我们在做几何证明推理题时，要做到“心中有已知，眼中有图形，证明有结论”，这样就可以比较顺利地写出几何证明题的推理过程。

参考文献：

钱华.初中几何证明教学研究[J].湖南师范大学，2008（7）.