试论数形结合法在高中数学教学中的优化应用

朱小燕

当前，我国实行全面的素质教育，在高中数学教学过程中，数学是一门较为抽象的课程，在学习过程中具备一定的难度，导致很多人对于数学的学习兴趣不高.相关实践研究发现，在高中数学教学中运用数形结合教学方法，不但可以帮助学生培养出自主探索的学习精神，还能够促使学生在自由交流的过程当中全面提升数学技能、加强对数学思想的认识和理解.

一、数形结合的重要意义

对于高中数学来说，形象化、抽象化以及符号化都比较强，若学生形象思维能力不够强容易在学习过程中产生吃力感，影响学习信心.而数形结合具有其它教学方法无法比拟的优势，被广泛地运用在教学中，它具有灵活性、规律性等特点.它根据“以形助教，以数解形”使抽象复杂的数学问题可以简单化，容易化，可以使学生的理解能力、分析能力、观察能力，综合能力得到提升，为学生的数学学习提供有利条件，有助于数学成绩的提高.

二、数形结合思想方法在高中数学教学中产生的积极作用

1.有利于学生降低对数学概念的理解难度

对于高中数学来说，大多数概念都非常抽象，增加了理解的难度，促使学生产生乏味感.同时，很多复杂、类似的公式容易导致学生出现混淆不清现象，无法正确运用在实际解题当中，容易降低学生的学习兴趣.通过运用数形结合的思想方法，可以把概念进行图像化，直观化，让学生们通过观察图像去进行分析，在很大程度上降低了学习的难度，进一步加强了学生对概念的理解，消除因学习难度大而带来的挫败感.

2.帮助学生掌握所学知识

在课堂上.老师一般都是进行概念性和理论性知识的讲解.并且要求这些学生可以在课后进行复习和回忆.为实际应用打下扎实的基础.在数学教学中，它们是紧密联系在一起的，缺一不可.老师会用形象的语言来表达抽象的数学知识，让学生们在脑海中可以构建出一个基本的数学模型，然后再加深对数学基本概念和公式的讲解，最后是示范出相关的例题，进行实际运用.例如：在实际数学教学中，通过利用数形结合的方法，能够为创建几何模型提供思路，进而把问题复杂性简单化，让学生直观的看到问题本质，有效降低了学生学习的难度，从而进一步提高对于数学学习的兴趣以及信心.此外，在学习函数的时候，学生们对于二次函数感到难于理解，特别是在其增减性和单调性的理解上更是感到困难，数学教师还可通过图象把抽象的数学问题直观明了地画出来，让学生们通过对图象的观察和了解，进一步了解二次函数的增减性和单调性.

二、数形结合结合在高中数学教学过程中的具体应用

在高中数学教育的所有方法中，数形结合的思想教育方法是其中一个效果较为显著的教学方法，它贯穿于整个高中数学教学的所有方面.现通过以下几个具体案例的详细分析，来进一步证明这一思想方法的有效性.

1.数形结合在理解函数性质中的应用

高中数学的知识大多数都是既抽象又空洞，对学生们的立体空间思维和想象力要求较高.很多学生在学习起来感到非常的吃力，为了加强对概念公式的理解，可以通过画图把概念含义性质直观地表示出来，一目了然.例如，在高中数学的三角函数运用中，有很多关于tanx、cosx、sinx相关的函数性质，教师在课堂上可以把其相关的图象画出来，然后再慢慢地分析其相关性质，了解函数的增减性，单调性，最大值，最小值，周期性，奇偶性等，这样不仅把抽象问题化为直观，降低学生们的理解难度，更可以提高学生们的学习兴趣，加深对sinx等函数的了解.

2.数形结合在判断函数奇、偶性上的具体应用

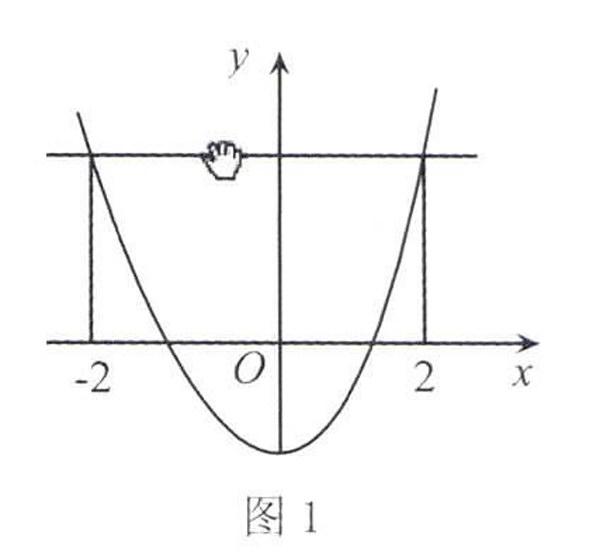
很多学生在学习高中数学函数的时候，常常无从下手，找不到解题的关键，尤其是在奇函数和偶函数的区别上更是模糊不清，每当遇到这样的情况，就应该通过数型结合的办法来打开解题的卡口，对函数的奇偶性作出正确判断，以及找出函数的正确值域.例如在讲解偶函数这个知识点的时候，以y=f（x）为例子，且其在区间（-∞，0）上为减函数，f（2）≤f（a），让学生根据题目所给出的条件，把a的真正取值范围计算出来.对于此类型的函数，[TP7GS25.TIF，Y#]抽象感比较强，若是仅仅通过数学推导的方法来进行，学生会感到难度非常大，但是如果通过画图分析，则会大大降低解题的难度.为此，在对该类问题进行解题的过程中，应该要把其对应的图像画出来，详细如图1.

通过对图1的仔细分析与观察，可得知y=f（x）属于一个偶函数，只要按照题目给出的条件，就可以计算出a的实际取值范围.此题解题的关键为图象，图象直观地把函数的本质展示了出来，让学生更加容易去掌握进而找到解题的关键所在.同时，促使学生积累了解决该类题目的经验，在日后再次遇到类似问题，学会有效利用数形结合方法提高解题效率.

3.数形结合在判断函数求最大值中的运用

观察，寻找出正确的解答步骤.经过与老师的仔细商讨以及分析之后，可知图中阴影部分就是该函数的可行域，进而找到了正确的答案.通过数形结合的方法，不但保证了解题的准确性，同时也提高了解题的效率.

从以上就是几个把数形相结合起来，达到成功解题的案例.再一次充分证明了数形结合思想方法在高中数学教学中的有效性.在整个过程中，学生们通过自己的深入思考和分析，寻求出正确答案，得到情感上的自我满足.

以上所述可知，数形结合是一种行之有效的教学方法，它可把抽象化为直观，不但有利于提高学生对数学学习的兴趣，进一步降低学生的理解难度，还有利于

培养学生自主探索以及坚持不懈的学习精神.为此，在我国高中数学教学中，应对数形结合教学放大大力推广并且运用，借此从根本上提高数学教学质量.