慢就是快
2016-05-14张丽莉
张丽莉

“慢就是快”这句话,通常是用来劝慰性子急的人做事耐心些,速度放慢些,防止急躁做事出现意外事端,反而延误事情的完成。对这句话诠释最贴切的是浙江的一种毛竹。这种毛竹种下后,即使农民们一直精心照顾,往后4年也只不过缓慢地长出3厘米。但第5年后会以每天足足30厘米的速度生长,只要6周就可以快速地长到15米。人们忍不住惊叹:为何有如此惊人的生长速度?原来在慢生长的前4年,毛竹将根深深地扎进数百平方米的土壤里,才得以成长如此迅速。
“慢就是快”其实是一个辩证的话题,它常常与“欲速则不达”联系在一起。放在特定的教育领域中,同样让人深思。在笔者身边就真实地发生过这样一件事:一位不想让孩子输在起跑线上的妈妈,让才上幼儿园中班的儿子开始做二年级的两位数加减两位数的计算,对于这个年龄段的孩子来说,只要求认识10以内的数即可。“聪明”的妈妈利用自己的学习经验将两位数加两位数的竖式计算传授给儿子,孩子乖巧地听从,单纯地模仿,也能将结果算出来。妈妈开心地说自己的儿子真聪明!事实上,孩子对两位数没有概念,没有对两位数的组成的认识,也没有对两位数的大小排列的认识,更谈不上对两位数加减法算理的理解(类似满十为什么要向前一位进一等)。孩子能计算出结果只是表面的。根据多年的教学经验,我们预测到,若再让这个孩子学习计算三位数加减三位数时,这位妈妈势必又要花费好长的时间,效果还并不一定如人所愿。如此揠苗助长的学习违背了孩子的年龄特征及学习规律,也违反了学生的身心发展规律。主张“教育是慢的艺术”的张文质指出:我们真的太强调立竿见影,太强调效果了。教育需要给孩子更大一点可以腾挪的空间,这才可能是好的教育。
纵观小学数学课堂,我们一直依照新的课程标准的理念尝试改变着,从“要我学”转变成“我要学”,再发展到“我会学”,这期间发生着从量变到质变的过程。但是课改下的课堂也仍然存在不和谐的现象:课堂上急于知识点的传授,而忽视了学习能力、品质的培养;急于形成学习技能,而缺少了数学文化的熏染;急于关注教学效果的整齐划一,而忽略了学生个性化的发展。造成这些现象的原因正是我们的课堂教学太过于追求速度。在快速的课堂中,学生们能得到什么?囫囵吞枣般地学习,如同嚼着白蜡般的食物,不能品尝到食物的鲜美,更没有体会到品尝美味后发自内心的快乐。《重庆时报》曾发表一篇文章,指出:“快”出来的社会是危险的。那么,“快”出来的教育安全吗?
《义务教育数学课程标准》(2011年版)指出:课程内容的组织要重视过程,处理好过程与结果的关系。那么我们小学的数学课堂的学习过程能否再慢一些,腾出足够的自我空间,让学生自主地感受、体验、顿悟?这样他们才能更牢固地理解数学知识,更深刻地掌握数学方法,更深远地感悟数学思想与价值。这才是我们希望看到的结果。
一、慢慢纠错,才能更牢固地领悟知识
《义务教育数学课程标准》(2011年版)指出:学生的学习应当是一个生动活泼、主动和富有个性的过程。在课堂教学中,如果我们忽略了学生个性的积极参与,教学会显得呆板、单调。数学学科本身就具有精准的特质,很容易让有些教者粗浅地认为只要传授正确的答案,学生们顺从地接受了便是掌握。而往往事实上在教师传授的过程中,每个学生听到的,学到的会存在差异,甚至出现错误,从而偏离我们预想的期望值。
例如:《角的初步认识》是二年级下册的教学内容,这是学生首次正式地学习平面图形,需要通过教学,初步感知角的基本特征,并能正确地识别角与判断角的大小。对于角,学生们并不陌生,生活中有许多实物都有角。也就是说,学生有此类知识的生活经验,更具体地说有着直观角的感受。很多教师在教学中都会从实物中抽象出角,在此之前,教师都是让学生们在实物中找到角,并用手指出角,经常出现学生只指尖尖的顶点处,有的学生随意地摸一摸角的两条边的现象。各不相同的错误指法让很多教师无法突破这一教学难点,只好生硬地告诉学生:“其实角是这样指出来的,谁模仿老师再来指一指角呢?”因为指角的过程可以渗透画角的步骤,于是学生开始千篇一律地模仿记忆,至于为什么要这样指角不得而知。可是,笔者在一次活动中看到了这样不同的教学处理:
1.出示五角星。
师:知道为什么叫五角星吗?
生:因为它有五个角。
师:它的五个角在哪儿呢?
(学生上台指角,摸了摸尖尖的顶点处,此时,教师没有对指角的正确与否给出评判)
师:老师想描下一个角?除了用到铅笔,还需什么?
生:尺子。
(师示范描角)
2.出示例题图。
(学生找出图中的角,随意描角,教师不作任何要求)
(展示学生描出的角,抽象出一个个角,并揭示课题:认识角)
3.学生画角。
师:不描,会画一个角吗?
(生画角,并展示,课件随后出示之前抽象出的角)
4.比较。
师:比一比,课件上的角与你自己画的角有什么相同的地方?
生1:角是尖尖的。
生2:都有直直的线。
5.学生自学课本认识角各部分的名称,顶点与边。
(学生指出所画角的顶点与边)
(出示:小小角,真简单,一个顶点两直边)
6.学生再次画角,并说出画角的过程。
执教以上片段的教师没有刻意让学生指角,而是在慢慢悠悠中改正了学生的错误指法并让学生逐渐明白了角的画法。第一次指角,学生是错误的,可是教师没有追究,而是选择“宽容”地对待,允许他们原生态地展现自己的学习状态,事实上学生在经历描角的过程中,已经在悄悄地感受着角各部分的组成。第二次教师选择让学生自己画角,有错误,教师还是淡定自如地继续,也没有过多地干涉学生的学习,只是让学生比一比不同的角的共同特点,学生在比较中发现角的特征继而认识了角各部分的名称。通过儿歌的形式,让学生趣味性地记住了角,虽简短,但精练,还隐含着角的画法——先画顶点后画两边。看似没有及时地指出学生的错误,事实上是让学生们在经历学习的体验中自己不断修正的过程,教师慢慢“陪读”的过程就是等待学生自我内化的过程,最后那些错误的指法水到渠成地得以纠正,画角的步骤也不攻自破,学生对角的特征的理解与掌握更到位、更牢固。
二、慢慢完善,才能更深刻地习得方法
教育学者张文质指出:教学需要学会等待。因为每个人都会有智慧的觉醒,有一个精神力量增长的过程,自我意识的形成过程,所以教师要有等待之心。课改曾提出“向40分钟课堂教学要质量”,所以有些教师将质量等同于数量,错误地以完成了多少教学任务作为衡量的标准,继而在课堂教学中不愿意将太多的教学时间投入到让学生自由表达意见的环节,生怕耽误了教学进度。似乎只有教者的讲解更为准确,方法得当。其实放手让学生们说说自己的想法,他们在不断的交流中,想法也会像潮水一般喷薄而出。
这是一道本区调研卷中的题目:
两个数的差是265,如果被减数不变,减数增加26,那么现在的差是( )。
A.265 B.291 C.239
本题考查学生对减法的一个规律的理解,即被减数不变,减数增加,差变小。
课堂上,教者放手让学生说说本题是怎么解答的。
生:如果被减数是365,减数是100,那差就是265。题目中说被减数不变那还是365,减数增加26,就是126,差就变成了239。
师适时提问:刚才这位同学说的你们懂吗?
生齐声回答:懂。
师:他是用什么方法让你懂的?
生:举了个例子。
师:你也会举这样的例子吗?
学生们跃跃欲试,不一会工夫,好多小手举了起来。
生:老师我的例子比他更简单。我把被减数就看成265,减数就是0,根据题目要求现在的差就是265-26=239。(这名学生在举例上比前者要优化些)原来大家都想让解决的方法简单些。
师适时追问:不举例也可以解决这个问题吗?
有学生立刻反应过来,并迫不及待地说:其实减法中有一个规律:就是被减数不变,减数变大,差变小。
师:是有这么一个规律。谁能说说,你是怎么理解的呢?
一个机灵的小男孩站起来说:我们还是可以举例啊。假如我原来有265元压岁钱,没有给我妹妹,我还是265元钱,如果现在要多给妹妹26元,那么我自己剩下的钱就会少了。
师相机追问:少多少呢?
生:26元。
师:怎么是26元呢?
生:你想啊,我少的那部分就是我多给妹妹的那部分,也就是减数增加的那部分呀!
笔者不禁为这名学生鼓掌,显然他已经从实例运用不完全归纳法得出规律,再将规律投射到具体实例中。他们自主经历了一个从直观到抽象的归纳过程,并在这样的过程中学生们习得了解决实际问题的方法——举例。更让笔者惊喜的是下面的片段:
师:如果我把这道题改变一下呢?
两个数的差是265,如果减数不变,被减数增加26,那么现在的差是( )。
A.265 B.291 C.239
生:还可以继续用刚才××说的例子,现在就变成妈妈多给26元压岁钱,但是给妹妹的还是不变,自己的钱就会变多,多26元。
生:其实就是被减数增加了,减数不变,差就会跟着增加。
概括得多好啊,语言精练完整清晰,其他学生不禁为他鼓掌。
师:是啊,减法里除了有这两个规律外,还有其他的规律吗?
思路拓宽后,学生们开始自主探索起来,巡视的过程中,我发现大部分学生在通过举例的方法寻找规律,很快概括出:被减数增加,减数也增加,差不变。很多学生默默点头表示认可,教者微笑地等待着。
师:如果被减数增加10,减数增加5,差也不变吗?
片刻宁静之后,一生道:“要一样。”此语一出,众人豁然开朗,叫道:“被减数和减数要增加的数一样,差才不变。”是啊!此刻学生们明白规律的得出是需要严谨归纳的,要在变和不变中抓住本质。
此时下课铃响了,教师问:“不知道加法里有什么样的规律哦?”一石激起千层浪,教师宣布下课后,竟然没有学生愿意下课,一个个埋着头举起例子来。
以上这节课中大量的时间放到了解决试卷中的这道题上,从教学进度来说,慢了,确实慢了,这么长的时间仅仅解决了一道题。但是从学习效果来说,却是倍增的。学生们从这道题中收获的不仅仅是减法的规律,或者是课后自主探索的加法的规律,他们更收获了探索规律的方法。相信在以后的乘除法或者其他数学规律的探索中,他们早已不需要教师花费更多的时间,也都会自觉地运用例举的策略解决问题。这里显性的“慢”只是过程的慢,而结果会让我们收获更多的精彩。
三、慢慢建构,才能更深远地感悟价值
日本学者佐藤学曾经说过:教育往往要在缓慢的过程中才能沉淀下一些有用的东西。数学学习也是如此。数学是一门为学生提供认识自然现象、社会现象和客观规律必需的数学基础知识和基本技能的学科,这也是它的知识价值。学生凭借已有的知识,在生活化的活动情境中,用自己的方式去尝试解决问题,经历知识的发现、发生、发展过程,这样的数学知识,学生才会感到有趣、有味、有价值。
复习课往往是教师们容易忽视的,常常存在“题海战”“大杂烩”的现象,因为内容是已学的,学生们感觉似乎都懂了,所以学起来也没有兴趣。事实上,特级教师许卫兵指出:复习课也是数学学习的重要组成部分,它同样承载着数学学习的应有价值,即:帮助学生学会思考,发展思维,提升数学素养,培育数学情感。
例如,苏教版三年级下册《长方形和正方形的面积复习》,教者在梳理归纳完面积、面积单位、面积计算、面积和周长的关系之后,设计了这样的练习供学生们对比研究:
师:用一根24厘米长的线,你能围成一个怎样的长方形呢?动手画一画,试一试。
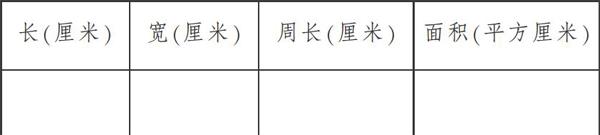
(学生以小组为单位进行研究,有的用事先准备好的小棒摆,也有的动手在纸上画。并填写表格)

(不一会儿学生开始各抒己见地汇报)
生1:我们小组研究的长方形:长是11厘米,宽是1厘米,周长是24厘米,面积是11平方厘米。
生2:我们小组研究得出这样的长方形,长是7厘米,宽是5厘米。周长是24厘米,面积是35平方厘米。
……
师:说了这么多不同的长方形,能按顺序整理出来吗?
(师生共同整理)
师:你有什么发现吗?
生:周长都一样,面积不一样。
师:为什么周长会一样?
生1:因为都是用24厘米长的线围起来的。
生2:长在变短,宽在变长。
生3:当长和宽一样的时候,面积最大
生4:是的,长和宽愈接近,面积就愈大。
师:是的,用24厘米长的线围成正方形时面积最大。可是在围的过程中,我们是不是可以借助其他物体,让24厘米长的线能围出一个面积更大的正方形呢?
(一石激起千层浪,学生们兴趣的小火苗又被点燃了)
很快出现了三种不同围法:
第一种:一边靠墙,24厘米的线围三边。
第二种:两边靠墙,24厘米的线围两边。
第三种:三边靠墙,24厘米的线直接成一边。
以上教学片段中,教师始终站在后面,慢慢地让学生们的思维不断向前奔跑。数学学习的关键就在于数学思考,在于思维的开放性、多样性、深刻性……学生在慢慢围长方形的过程中建构起长宽变化与面积变化之间的关系,在慢慢围更大正方形的过程中,学生感受数学研究视角的变化所带来的不一样的震撼。而这种带着困惑与挑战的“印记”,让学生体验到数学学习的成功与惊喜,感悟到数学价值与魅力。
我们生活在一个被“快”字追赶和激发的时代,但是我们的课堂教学理应崇尚“慢”,因为每个孩子都是一朵含苞待放的花蕾。只有成长的过程中慢慢吸足了养分,才会有令人夺目的绽放,因为生命的成长需要沉淀,需要教者们陪着孩子们慢慢走,慢慢欣赏过程中的点滴,无论是快乐,还是痛苦。如同台湾作家龙应台写道:“我,坐在斜阳浅照的台阶上,望着这个眼睛清亮的小孩专心地做一件事;是的,我愿意等上一辈子的时间,让他从从容容地把这个蝴蝶结扎好,用他五岁的手指。孩子慢慢来,慢慢来。”课堂教学中我们只要慢些、再慢些,也许你会看到孩子们更快地生长!
