在风险和不确定性情况下对具有关联性的交通投资进行最优化决策

李宗志

摘要：本文通过分析目前的交通投资决策过程、交通项目评估方法和交通项目选择方法，指出现有方法的局限性，提出本次研究的任务是选取候选项目的最优子集，以实现效益最大化，并可以明确解决三个问题，一是项目全局影响，二是项目效益的整体风险，三是同时实施多个项目时项目间的关联性。

关键词：交通项目；评估；成本分析；背包模型

中图分类号：U121 文献标识码：A 文章编号：1006-7973（2016）07-0010-02

选取候选项目的最优子集，以实现效益最大化，并明确解决以下问题：

项目全局影响；项目效益的整体风险；同时实施多个项目时，项目间的关联性。

1 评估项目全局影响的方法

我们使用“多种商品最低成本网络模型”计算项目实施前后每条路段上的交通量和车辆构成。这些数据对估算单个工程和多个工程的交通管理部门效益和用户效益至关重要。

致力于大规模仿真分析的芝加哥TRANSIMS软件被用来执行“多种商品最低成本网络模型”：

2 交通项目评估方法

路面生命周期交通管理部门成本：

用户成本组成：车辆运营成本，出行时间成本，事故成本，车辆尾气排放成本：桥梁项目生命周期交通管理部门成本分析：

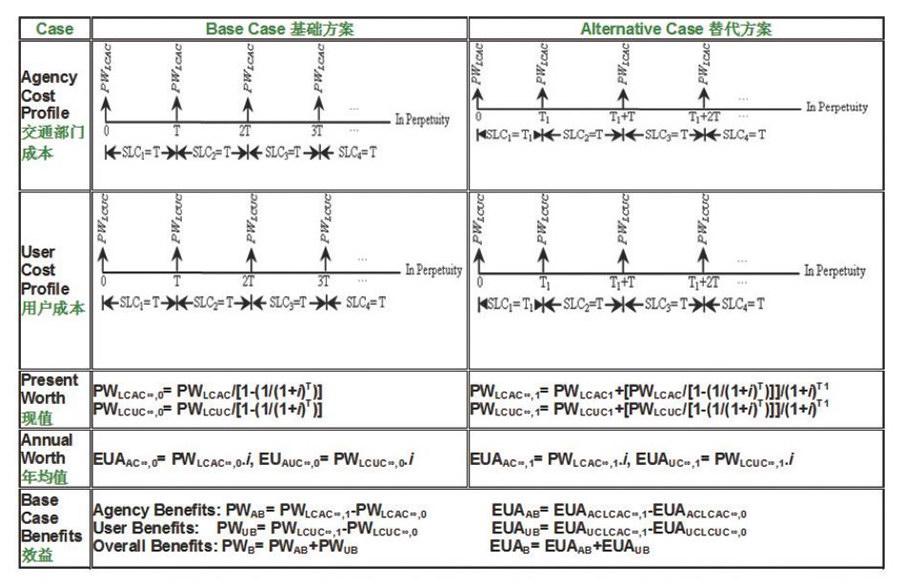
3 交通项目在永久性生命周期中的效益

交通项目生命周期成本分析的风险和不确定性。

确定性，风险，不确定性分类：

（1）确定性：单一结果

（2）风险：知道结果的分布范围和分布函数

（3）不确定性：不知道范围，或者知道范围但不知道分布函数

主要的风险和不确定性因素：建设，翻修和养护成本；交通需求；折现率

基于风险的生命周期效益一成本分析方法

我们选择Beta分布来模拟基于风险的输入参数的概率分布：

Beta分布中，最大值和最小值都是非负数，且可能的结果是对称或倾斜的；

基于不确定性的生命周期效益一成本分析方法；

谢克尔模型非常适合处理输入参数的不确定性；

该模型对每个输入参数生成三个值。

Shake模型的延伸：基于对每个输入参数生成的三个值，我们可以引入一个决策规则来最终确定输入参数的值。

如果输出结果越高越好（交通增长率，用户成本梯度）。选择项目的方法一新模型1：两阶段背包模型第一阶段优化：算出项目效益总风险的最小值柯维茨均值一方差模型：

可用于一个项目的预算比例：

每对项目的效益协方差：

第二阶段优化：将第一阶段得到的项目效益总风险的最小值用作随机模型中项目效益风险的上限。

新模型2：超图背包模型

计算全局效益时，项目之间的关联性可以这样计算：

新模型3：两阶段超图背包模型

第一阶段优化：使用马柯维茨均值一方差模型求出项目效益总风险的最小值。

第二阶段优化：将第一阶段优化中求出的最优解作为超图模型中项目效益总风险的上限。