有关折弦定理的几个推论

吴文龙

摘 要：折弦时常应用于初中数学竞赛试题中，对数学竞赛的辅导与学习具有良好的作用，证明了著名的“阿基米德折弦定理”的逆定理及几个推论，以后可直接运用。

关键词：折弦；定理；推论

在同一圆上有公共点的两条弦组成一条折弦。折弦时常应用于初中数学竞赛试题中，对数学竞赛的辅导与学习具有良好的作用，值得研究和探讨。下面讨论几个有关折弦的命题。

命题1：如图，若弦AB、BC组成⊙O的一条折弦，BC>AB，D是弧ABC的中点，DE⊥BC，垂足为E，则E是折弦ABC的中点，即CE=BE+AB.

此命题即著名的“阿基米德折弦定理”。此命题的证明是不难理解的，有此定理的11种证法。

该定理常规的证明方法有以下几种：

阿基米德折弦定理证法1：补短法

如图，延长DB至F，使BF=BA

∵M是弧ABC的中点

∴∠MCA=∠MAC=∠MBC

∵MBAC四点共圆

∴∠MCA+∠MBA=180°

∵∠MBC+∠MBF=180°

∴∠MBA=∠MBF

∵MB=MB，BF=BA

∴△MBF≌△MBA

∴∠F=∠MAB=∠MCB

∴MF=MC

∵MD⊥CF

∴CD=DF=DB+BF=AB+BD

阿基米德折弦定理证法2：截长法

如图，在CD上截取DG=DB

∵MD⊥BG

∴MB=MG，∠MGB=∠MBC=∠MAC

∵M是弧ABC的中点

∴∠MAC=∠MCA=∠MGB

即∠MGB=∠MCB+∠BCA=∠MCB+∠BMA

又∠MGB=∠MCB+∠GMC

∴∠BMA=∠GMC

∵MA=MC

∴△MBA≌△MGC

∴AB=GC

∴CD=CG+GD=AB+BD

阿基米德折弦定理证法3：垂线法

如图，作MH⊥射线AB，垂足为H

∵M是弧ABC的中点

∴MA=MC

∵MD⊥BC

∴∠MDC=90°=∠H

∵∠MAB=∠MCB

∴△MHA≌△MDC

∴AH=CD，MH=MD

又∵MB=MB

∴Rt△MHB≌Rt△MDB

∴HB=BD

∴CD=AH=AB+BH=AB+BD

命题2：如图，若弦AB、BC组成⊙O的一条折弦，BC>AB，D是折弦ABC的中点，DE⊥BC，垂足为E，则E是弧ABC的中点，即CE=AB+BE.

此命题是命题1的逆命题，就称“阿基米德折弦逆定理”。证明也不难理解，延长CB到A′，使BA′=BA，连接CE、EA′、AA、EA即可得证。

这两个定理体现了数学的和谐美，由这两个定理不难联想到以下两个有用命题。

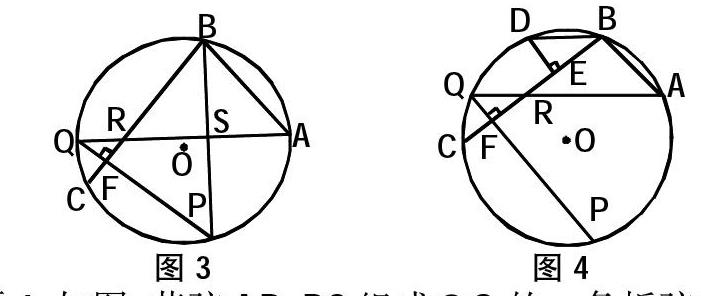
命题3：如图，若弦AB、BC组成⊙O的一条折弦，BC>AB，P是弧AC的中点，PQ⊥BC，垂足为F，交⊙O于Q，AQ交BC于R，则

（1）CF=RF；

（2）PB垂直平分AR；

（3）AB=BR.

证法：连接CQ，先证△CQF≌△RQF，得到CF=RF；

再证△ABS≌△PBS，得到PB垂直平分AR，AB=BR.

命题4：如图，若弦AB、BC组成⊙O的一条折弦，BC>AB， D是弧ABC的中点，P是弧AC的中点，DE⊥BC，垂足为E， PQ⊥BC，垂足为F，交⊙O于Q，AQ交BC于R，则

（1）BE=CF；

（2）AB=EF；

（3）DE∥QF， DE=QF；

（4）DB∥AQ.

此命题可由命题1和命题3加以证明，证明过程略。

参考文献：

[1]周春荔，张宁生.数学奥林匹克教材（普及版）[M].北京：首都师范大学出版社，1994.

[2]张昕.一道初中竞赛题的证法探讨[J].中学数学教学参考，1999（3）：32-33.

？誗编辑 孙玲娟