“直线与圆的位置关系”说课案

霍志峰

今天我说课的题目是人教A版必修二第四章第二节《直线与圆的位置关系》，本节课我将基于教什么、怎么教、为什么这么教，从以下五个方面阐述我的教学设想。

一、教材分析

直线与圆的位置关系是对圆的方程应用的延续与拓展，又是后续研究圆与圆的位置关系及直线与圆锥曲线的位置关系等内容的基础。在直线与圆的位置关系的判断方法的建立过程中蕴含着诸多的数学思想方法，这对进一步探索研究后续内容有很大的启发与示范作用。因此本节课具有承上启下的作用。

二、学情分析

初中学生已经直观讨论过直线与圆的位置关系，前阶段又学习了直线与圆的方程及圆的有关性质，虽然对这部分内容比较熟悉，但对如何利用坐标法判断直线和圆的位置关系和数形结合思想的应用还有待探究和提高。

三、目标分析

1.教学目标

知识与技能：掌握根据直线和圆的方程判断它们位置关系的方法；熟练运用直线和圆的位置关系解决有关问题。

过程与方法：通过观察实际中的问题情境，将之化归为判断直线和圆的位置关系问题，逐步形成用代数方法解决几何问题的坐标法思想；领悟数形结合的魅力，提高发现问题，分析问题，解决问题的能力。

情感、态度与价值观：关注知识的生成过程，使学生养成问问题的习惯及勇于发现、主动探索的精神，让学生感受学习的成功与快乐。

2.教学重点、难点

重点：利用方程判断直线和圆的位置关系的方法。

难点：直线和圆的位置关系的灵活运用。

四、教法、学法分析

1.教法分析：运用启发式教学方法，创设问题情境，调动学生求知欲，激发学生的探究心理。

2.学法分析：贯彻以学生为主体的探究式学习。通过自学、观察、尝试演算获取知识，在探究过程中，学生的分析、归纳和推理能力得到提高。

五、教学过程分析

环节一：创设情境，引入新课

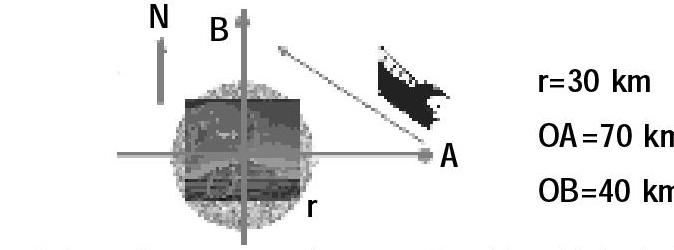
我国对钓鱼岛周围30 km的圆形区域实行警戒防御，现发现在钓鱼岛正西70 km处有艘日本船，前往钓鱼岛正北40 km处，若日本船只沿直线行驶，请问同学们我国是否采取军事行动予以驱赶？

【设计意图】通过对引例的改编，利用钓鱼岛创设情境，引入新课，提高学习兴趣，体验数学与生活的密切联系。

环节二：探索研究，构建新知

问题1：你能用初中的平面几何知识解决这个问题吗？

问题2：能否用直线与圆的方程来解决这个问题？

【设计意图】通过问题引领方式，引导学生主动回顾初中所学直线与圆的三种位置关系及判断方法，进而引发新知识增长点，为接下来例1的学习做好铺垫。

问题3：例1：已知直线l：3x+y-6=0和圆x2+y2-2y-4=0，判断直线和圆的位置关系；若相交，求交点坐标。

【设计意图】方法一：代数法，方法二：几何法，让学生体会两种方法的优缺点，培养学生思维的全面性。

环节三：反思过程，提炼方法

方法一：①联立；②消元，判断方程解的个数；③定位置关系。

方法二：①求圆心、半径，计算圆心到直线的距离；②比较距离与半径的大小；③定位置关系。

【设计意图】学生在教师的点拨下，根据例1的探究与板演展示，自己总结归纳解题方法。由特殊到一般，符合学生的认知规律。

环节四：课堂演练，强化方法

1.解决引入中的问题。

2.判断直线3x+4y+2=0与圆x2+y2-2x=0的位置关系。

3.已知直线y=x+2，圆C：x2+y2-2y-4=0，判断直线与圆有无公共点，若有，求其坐标。

【设计意图】让学生独立完成，巩固和检测学生对直线和圆位置关系的掌握情况，巡视解决可能存在的疑难点，并让其思考：（1）这道题还有别法吗？（2）这道题是否可以引申？

环节五：变式演练，深入探究

变式1：求例1中直线与圆所形成的弦长AB。

变式2：由点A（-2，2）引圆C：x2+y2=9切线，求切线方程。

变式3：求圆C：x2+y2+4y-21=0上的点到直线x+y-10=0的最大距离和最小距离。

【设计意图】通过变式演练，提高学生从不同方面掌握直线与圆的位置关系，进一步体会数形结合思想的优越性。

变式4：例2：过点M（-3，3）的直线被圆C：x2+y2+4y-21=0截得弦长为4，求直线方程。

【设计意图】通过例2的学习，培养学生举一反三的能力，进而提高学生分析、解决问题的能力和思维的严密性。

环节六：课堂小结，分享收获

1.直线和圆的位置关系的判断方法？

2.研究直线与圆的位置关系的主要方法？

3.本节课留给你印象最深的是什么？数形结合思想是我们高中数学学习的重要思想，作为课堂的延伸你能否总结一下我们所学的哪些内容还渗透数形结合思想？

【设计意图】新课程强调尊重学生的差异，鼓励学生的个性发展，所以课堂小结我设置总结性内容及开放性问题，期望这些问题使学生体验学习数学的快乐。

环节七：分层作业，自主探究

必做题：课本P132 习题4.2 A组1，2，3。

选做题：已知C：（x-2）2+（y-2）2=5的一条弦AB过点（3，1），且长为4，求直线AB的方程。

自主探究题：判断圆C1：x2+y2+2x+8y-8=0与圆C2：x2+y2-4x-4y-2=0的位置关系。

【设计意图】让学生巩固所学内容并自我检测与评价，让不同层次的学生都可以获得成功的喜悦，看到自己的潜能，并为下一课时学习圆与圆的位置关系埋下伏笔。

当然，在实际教学中，可能会受到若干因素干扰，这就要求老师沉着冷静，适时适度调整教学设计，以保证教学任务的顺利完成。最后以华罗庚的一首诗结束本次说课。

数缺形时少直观，形少数时难入微。

数形结合百般好，割裂分家万事休。

参考文献：

周建伟.巧用直线与圆的位置关系解题[J].数学教学研究，1999（5）.

？誗编辑 孙玲娟