初中数学教学中《图形与变换》的习题教学

赵婷婷

摘要：《图形与变换》是初中数学课程内容中关于平面图形和空间变换的一种知识体系，旨在培养学生的几何逻辑能力和空间思维能力。本文将实际的初中数学习题作为研究案例，分别对《图形与变换》课程体系中的基础性习题和辅助线的添加方法进行了全面而深入地分析探讨。希望能够在文中为初中的数学教师们提供相关方面的解题依据和教学参考。

关键词：初中数学教学；《图形与变换》；习题教学

中图分类号：G61文献标志码：A文章编号：2095-9214（2016）03-0066-01在初中数学当前的课堂教学过程中，习题教学是最常用也最有效的一种教学方式。新课标改革强调对学生思维能力的培养和提高。数学中的习题教学既能帮助学生迅速掌握数学知识和解题技巧，又可以在潜移默化中挖掘和激发出学生在数学思维上的实力与潜力。尤其是《图形与变换》这一单元的习题教学，对学生在几何图形数学思维上的空间想像能力和推理逻辑能力都有着正面的积极影响。

一、图形与变换基础习题的案例教学

在初中数学《图形与变换》基础习题的教学过程中，数学教师应该重点强化学生举一反三和一题多解的思维方式。通过极具变化性的平面几何图形和立体的变换关系，提高学生数学范畴内的空间想像能力和逻辑思维能力。

以图形变换基础数学习题中的翻折问题为例，这是中考数学试卷上的一种常见题型，主要考察初中学生对平面几何中轴对称变换的空间认知与性质理解。初中数学几何图形中轴对称的含义包括：平面几何图形中的对称轴是对应点连线的垂直平分线，同一夹角在翻折前后的对应角相等，同一图形在翻折前后的对应线段相等。当然，在应用这些原理知识解决实际数学问题的时候，还要结合勾股定理、相似原理和面积公式等，综合解题。

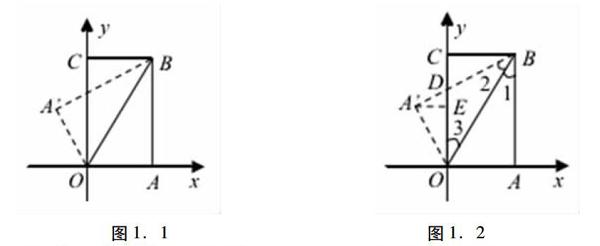
[例1]如图1.1所示，已知纸片OABC为矩形。将纸片平整地放在平面直角坐标系上，OA和OC分别落在了坐标系的x轴与y轴上。连接OB，把矩形纸片OABC沿着OB进行折叠。将点A翻折过后的落点标记为A。如果OB的长度为5，tan∠BOC=12。那么，点A在平面直角坐标系上应该表示为（）。

图1.1图1.2

[解析]根据题意可以求得，矩形纸片OABC中的AB=2，OA=1.

方法一：如图1.2所示，过点A作AE⊥OC于E。∵∠1=∠2=∠3∴OD=BD

假设BD=OD=t，可以推出DA=BA-BD=AB-BD=2-t

在直角三角形ODA中，∵OA2+DA2=OD2∴12+（2-t）2=t2t=54

RtΔODA的面积SΔODA=12×OD×EA=12×OA×DA

∵54×EA=34∴EA=35

依据直角三角形中的勾股定律可以得出OE=45

所以，点A在平面直角坐标系里的坐标为（-35，45）

方法二：如图1.3所示，过点A作FA⊥x轴，交x轴于点F，过点B作BE⊥FA，交FA的延长线于点E。

∵∠OAB=∠OAB=90°∴∠1+∠2=90°，又∵∠2+∠3=90°∴∠1=∠3

∵∠E=∠AFO=90°∴ΔOFA∽ΔBEA且相似比ΔOFA：ΔBEA=1：2

假设OF=t，则有EA=2t，FA=2-2t，EB=4-4t

由AF=BE4-4t=t+1可以算出t=35

∵FA=2-2t=45∴A（-35，45）

方法三：如图1.4所示，连接AA，交OB于点H，过点A作GA⊥x轴于点G。

∵A和A关于OB翻折对称∴AA⊥OB且HA=HA=25∠1+∠2=90°

又∵∠1+∠3=90°∴∠2=∠3

∵∠AGA=∠OAB=90°∴ΔGAA∽ΔOAB其且ΔGAA：ΔOAB=45：5=45

GA'OA=GAAB=45∵GA'1=GA2=45∴GA=45，GA=85，GO=35

所以，点A的坐标为（-35，45）

该题有三种解题方法，由于篇幅有限，在此不便做多讨论。

二、用图形变换的思想指导添加辅助线

在初中数学的平面几何中，辅助线的添加对解题思路有着关键性的帮助作用。有的时候，学生在看到已经答案解析中已经添加好的辅助线都不免惊叹，到底是怎样奇妙的数学思维，才能想出这样绝妙的辅助线添加法？《图形与变换》中的变换思想为学生指明了方向与出路。变换思维的最大特点就是平面图形在变形前后是完全相等的，只是在空间中的位置发生了一定的变化。

以二维图形变换思想中的位置平移为例，通过对平面图形进行合理的平移，使得原本分散的线索与条件集中到了一起。这种利用平移思维解决数学几何图形问题的解题方法叫做平移变换法。

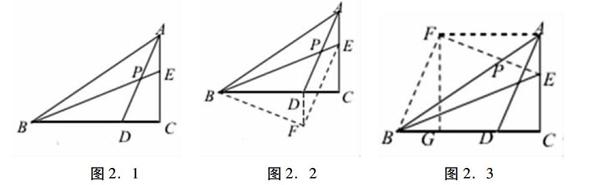
[例2]如图2.1所示，已知ΔABC中的∠C=90°，点D、点E分别是BC和AC上的点，AC=BD，AE=CD，AD和BE相交于点P，求∠BPD的夹角度数。

图2.1图2.2图2.3

[解析]∵ΔABC中的∠C=90°∴ΔABC为直角三角形。

方法一：如图2.2所示，过点D作DF⊥BC，在DF上取一点F，使AE=DF，得到平行四边形AEFD，且ΔACD和ΔBDF是相似三角形的关系。

假设BD=a，AE=b，则有BF=EF=a2+b2

∵BE2=BC2+EC2=（a+b）2+（a-b）2=2（a+b）2BE=2BF

∴ΔBEF是等腰直角三角形，∠BEF=45°

又∵AD//EF∴∠BPD=∠BEF=45°

方法二：如图2.3所示，将AD平移到BF的位置上。∵ΔBEF是等腰直角三角形∴∠BPD=∠BEF=45°

方法三：如图2.4所示，将BE平移到AF的位置上。∵ΔADF是等腰直角三角形∴∠BPD=∠DAF=45°

方法四：如图2.5所示，将BE平移到DF的位置上。∵ΔADF是等腰直角三角形∴∠BPD=∠ADF=45°

该题有四种解题方法，由于篇幅有限，在此不便做多讨论。

结束语

通过平面图形在空间上的变换，让晦涩抽象的数学思维变得生动具体，原本被局限于数字、计算和平面图形上的数学思想也被拓展到了立体空间的范围内。《图形与变换》的习题教学可以帮助学生有效提升自己在视觉上的图形感官能力和思维上的空间逻辑能力，是初中数学教学不可或缺的一种重要教学方式。

（作者单位：四川师范大学数学与软件科学学院）

参考文献：

[1]何佳. 初中数学中图形变换的相关教学研究[D].苏州大学，2011.

[2]包慧慧. 初中平面几何变换教学研究[D].内蒙古师范大学，2014.

[3]陈荣荣. 初中教师关于几何变换的认识及教学研究[D].首都师范大学，2009.

[4]左彩荣. 初中数学“图形与变换”习题教学研究分析[J]. 新课程导学，2014，31：85.