Adaptive control for an uncertain robotic manipulator with input saturations

Trong-Toan TRAN ,Shuzhi Sam GE,Wei HE

1.Center for Robotics and School of Automation Engineering,University of Electronic Science and Techno logy of China(UESTC),

Chengdu Sichuan 611731,China;

2.Department of Electrical and Computer Engineering,National University of Singapore,Singapore,117576;

3.Faculty of Electronic Technology,Industrial University of Ho Chi M inh City,Ho Chi Minh City,Vietnam;

4.School of Automation and Electrical Engineering,University of Science and Technology Beijing,Beijing 100083,China

1 Introduction

The control of robotic manipulator has gained great attentions in the field of automatic control and robotics comm unities due to its advantages of applications[1–5].dynamic model of robots is high nonlinearity and unknown exactly due to the payloads.Furthermore robots are usually restricted by physical conditions,and the input scalings are uncertain due to the transmission mechanism s[6–9].Neglect of the uncertainties or violation of the restrictions may result in undesired performance or system dam age.In this paper,w e address the control problem of uncertain robotic manipulator with taking into account the input saturations,unknown input scalings and disturbances.

The first specification of the above problem is to hand le the input saturations.The existing approach based on solving an optimal control problem with the input constraints was proposed in[10].Alternative approach is based on the concept of the saturation functions in[11,12].As shown in these works,for the trajectory tracking or the output tracking problem,the initial conditions are required to lie within a bounded region to ensure the satisfaction of input saturations.This means that the resulted system can only operate locally.The global stability is achieved only for the set-point tracking problem,i.e.,the position tracking problem as shown in[13].

The second specification is to deal with the uncertain parameters of the system.Due to the coupling of the variables and uncertain parameters in the model,in particular,the inertia and Coriolis and centrifugal forces matrices,the formers proposed the regressor approach to estimate the uncertain parameter in[14,15].Based on this approach,several adaptive controls have been developed such that adaptive inverse dynamics control in[16],adaptive passivity-based control in[17]and intermediate between the two approaches in[18].However,when the input saturations are taken into account,handling simultaneously both uncertain parameters and input constraints is problematic.The existing approaches[19–22]m ay not be directly applied due to constraints.Furthermore,when the input scalings are unknown and disturbances effect the system,the control problem becomes much more challenging.

Motivated by above consideration,we propose here a solution for the control problem of an uncertain robotic manipulator with taking into account the input saturations,unknown input scalings and disturbances.To deal with input saturation,our approach is to transfer the system with input saturation to the corresponding system with free control.This can be accomplished by using the MRAC-like,which is ISS and driven by the errors between the required control signals and saturations.The uncertain parameters are estimated by using regressor matrix,while the unknown input scalings and disturbances are hand led by non-regressor based approach[23].It is show n that the violation of input saturations is prevented,all the signals in the closed-loop system are bounded and the tracking error converges to the compact set which depends on the input saturations.Our design here is the extension of the work in[9].

The rest of the paper is organized as follow s.In Section 2,the dynamic model of the robotic manipulator and the control problem are provided.Section 3 presents the control design.Simulation results are carried out to illustrate the effectiveness of the proposed control in Section 4.The paper concludes in Section 5.

NotationRndenotes the Euclidean space withn−dimension.A∈Rn×ndenotes then×n−matrix.‖·‖is the Euclidean norm of vector“·”.is the minimum(maximum)eigenvalue of the matrix“·”.

2 Problem form ulation

In this paper,we study the robotic manipulator described by the following equations[12]:

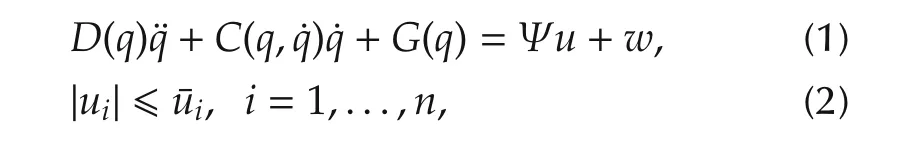
whereq∈Rnis a vector of the generalized coordinates;u∈Rnis a vector of control inputs satisfying constraint(2);¯ui＞0,i=1,...,nis the positive number;D∈Rn×nis the symmetric positive inertia matrix;C∈Rn×nis the Coriolis and centrifugal forces matrix;G∈Rnis the gravity force;Ψ ∈Rn×nis a matrix of uncertain input scalings;andw∈Rnis a disturbance vector,but know n bound,i.e.,there exists a positive number¯wsuch that‖w‖≤¯w.In this paper,we assume that all the states of the system are available for feedback.

The control objectives of this paper are:1)to track a desired trajectoryqd(t)∈Rnwhile all the signals in the closed-loop system are bounded and 2)the constraint(2)is satisfied.

It is noticed that the control problem here differs from the problem in[8].Since the controlusubjects to constraint(2),and the disturbancewis added.In comparison with the existing works in[11,24,25],the unknown input scaling Ψ makes the problem here more challenging.Before we move on the control design to deal with the arisen challenges,the following properties of the robotic manipulator(1)are needed.

Property 1[26]There exist the positive constantsdmanddMsuch that:

i)dm≤ ‖D(q)‖≤dM.

ii)Matrix˙D(q)−2C(q,˙q)is skew-symmetric if the matrixC(q,˙q)is defined by the Christoffel symbols,i.e.,

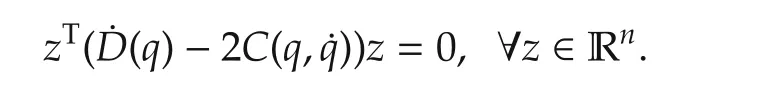
iii)The left-hand side of the(1)can be rewritten as

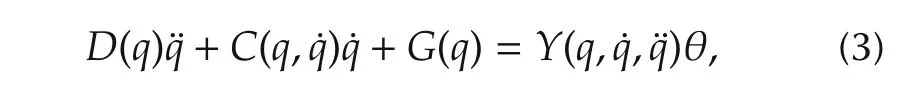
where θ∈Rℓis the vector of parameters,Y(q,˙q,¨q)∈Rn×ℓis the known functionregressor.

3 Control design

This section presents the control design of an adaptive bounded control for system s(1)and(2).Toward this end,we define the tracking error

and the filtered velocity variable

where Λ ∈Rn×nis a positive diagonal matrix.It is clear that if‖r‖is bounded then‖(p,˙p)‖is bounded.Furthermore,‖r‖→0 implies‖(p,˙p)‖→0.Accordingly,taking the time derivative of(5)along(1),we obtain the dynamic equation ofras

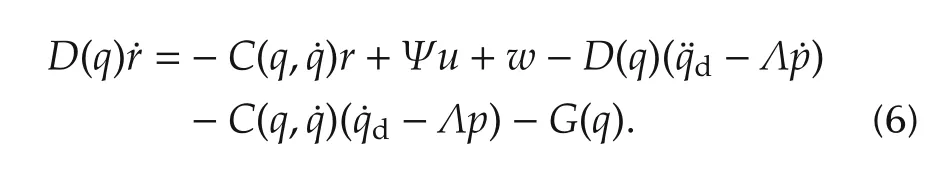
The term sD(q),C(q,˙q)andG(q)in(6)are unknown,we deal with these uncertainties by using the regressor matrix as follow s.Denoting

with the use of item iii)of Property 1,w e have

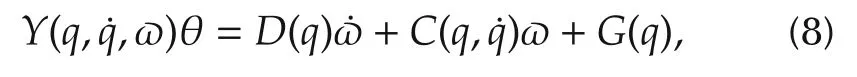
where θ ∈Rℓis the vector of unknown parameters andY(q,˙q,ω)∈Rn×ℓis the known function regressor.Then we rew rite(6)as

In view of(9),because Ψ is unknow n anduis restricted by(2),therefore the conventional adaptive approaches in[8,19,20]cannot be directly app lied.To deal with this situation,we firstly handle the uncertainty of Ψ by separating Ψ as

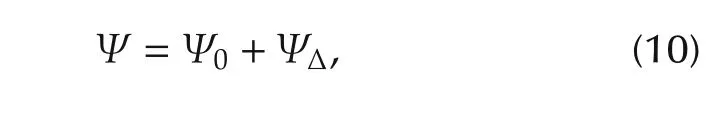
where Ψ0∈Rn×nand ΨΔ∈Rn×nare the known nominal and uncertain values of Ψ,respectively.

Assumption 1There exists a positive number ψmax＞0 such that

Since even we do not know the exact value of Ψ,but we can estimate the bounds of Ψ.Furthermore,Ψ ＞0 is the assumption as usual in the existing works[8,20].Therefore,Assumption 1 is reasonable.

Under Assumption 1,we rewrite(9)as

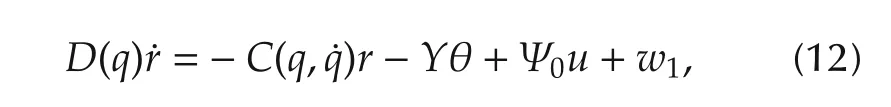
where

and it is bounded by

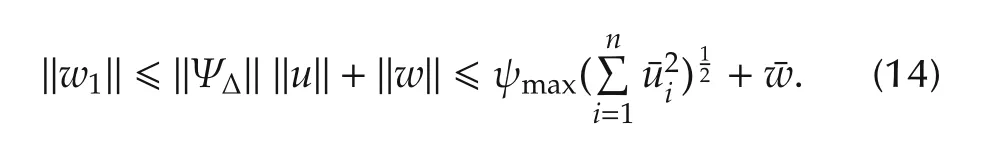
Consequently,we deal with the constraint(2).To do this,we use the control of the form[27]

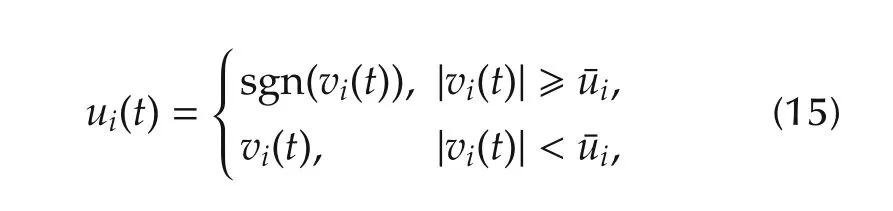
fori=1,...,nwhereviis theith control to be designed,and sgn(·)is denoted a signum function.Furthermore,we introduce the following reference model for(12)

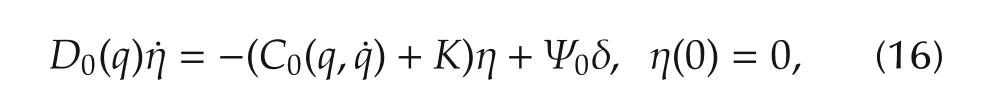
where η∈Rnis the auxiliary state;D0(q)andC0(q,˙q)are the priori estimations ofD(q)andC(q,˙q),respectively,with fixed parameters[16];K∈Rn×nis a positive matrix;and δ∈Rnis the corresponding input defined as

The following lemma show s that the model(16)is ISS.

Lemma 1Consider the system described by(16),if the matrixis skew symmetric,i.e.,then(16)is ISS with η as the state and δ as the input.Furthermore,if η(0)=0 then η(t)is bounded by

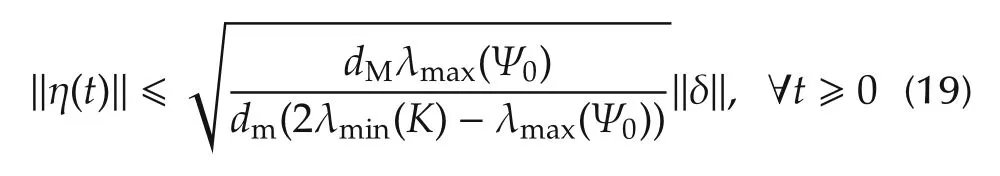
with 2λmin(K)＞ λmax(Ψ0).

ProofSee the appendix.□

Having Lemm a 1,w e denote

and subtract(16)from(12)with the use ofr=z+η,then we obtain the dynamic equation ofzas

Let

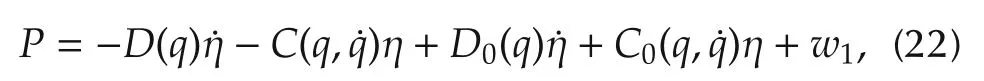
and(21)becomes

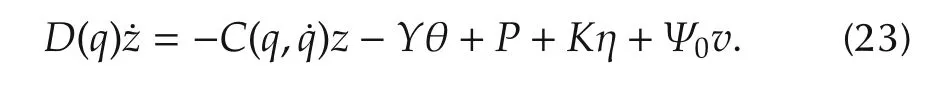
Obtaining(23),we have transferred(12)with the bounded controluto(23)with the free controlv.The prise of the transformation is that(23)is driven by the additional auxiliary state η of(16).

The goal now is to design the free controlvfor(23)such thatz(t)converges to a neighborhood of the origin.To this end,we need to estimate the bound ofPby the non-regressor approach in the following lemma.

Lemm a 2[23]Let Φ(η,˙η,˙q)be a scalar function defined by

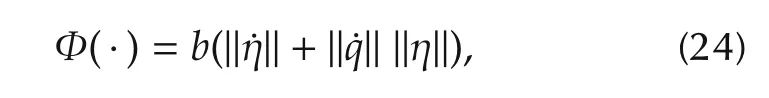
whereb≥1 is a known real number.Then the lumped nonlinearity and uncertaintyPin(22)obeys

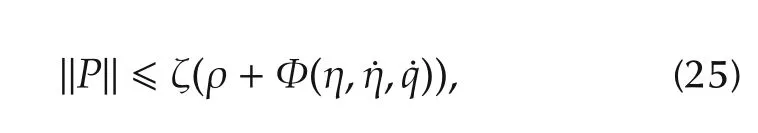
with ζ is a“normalized”unknown constant and ρ is a known constant.

ProofSee[23].□

In view of system(23)and(25),θ and ζ are the current unknown parameters.Letˆθ andˆζ be the estimations of θ and ζ,respectively,and w e propose the control of the form

where ε is a scale positive function(ε(t)＞0,∀t≥0)to be specified,and the update law s are

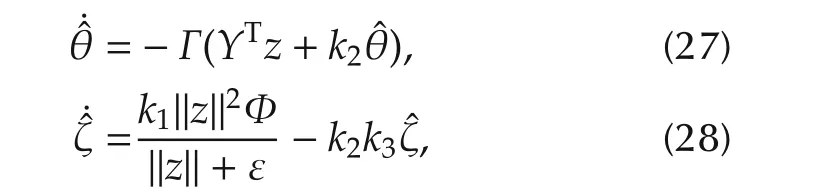
where Γ ∈Rℓ×ℓis a positive diagonal matrix,andk1,k2andk3are the positive numbers.

We have the follow ing results.

Theorem 1Consider the system described by(1)and constraint(2)under Assumption 1,the controluobtained by(15),andvobtained by(26)with the update law sanddescribed by(27)and(28),respectively.Then,the constraint(2)is satisfied and the following statements hold

1)The signalz(t)converges to a neighborhood of the origin which can be made arbitrarily small,i.e.,

where χ and γ are the positive numbers and γ can be made arbitrarily small.

2)All the signals in the closed-loop system are bounded.In addition,the tracking errorsp(t)and˙p(t)converge to the com pact sets Ω1and Ω2,respectively,defined as

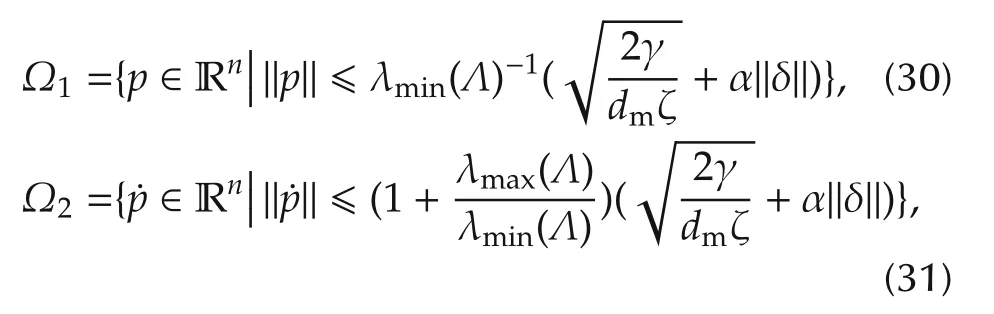
where α is a positive constant.

Proof1)Consider the candidate Lyapunov function

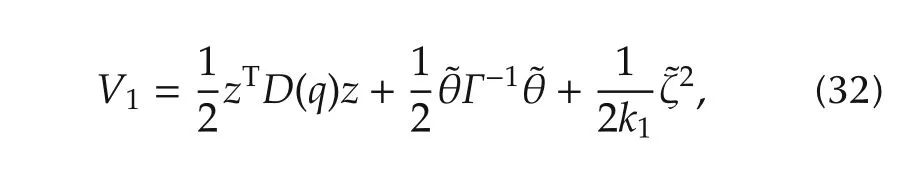
its time derivative along(23)is

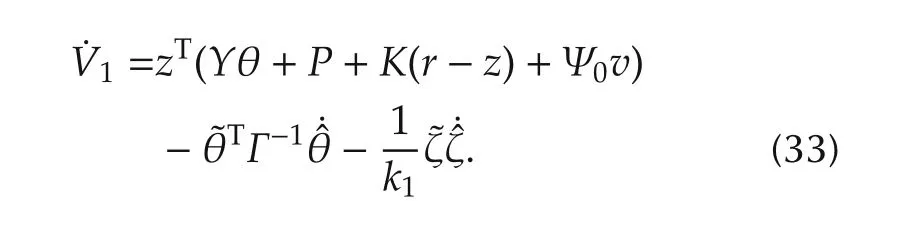
Substituting(26)–(28)into(33),we have

Using the estimation ofPin(25)of Lemm a 2,yields

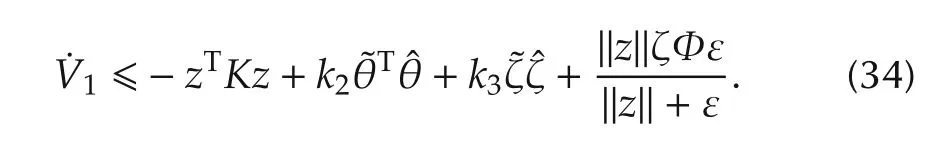
Choosingwherek5＞0 and using the following inequalities:

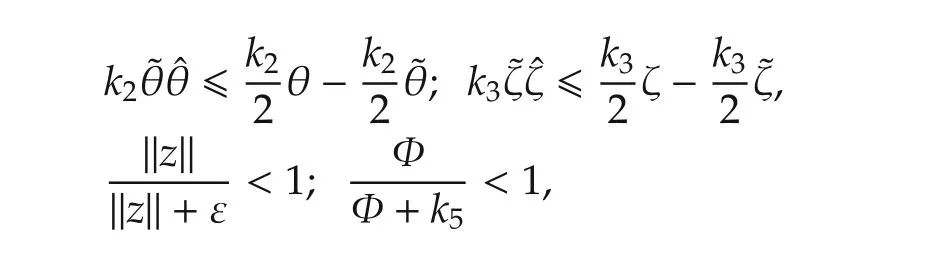
then,(34)becomes

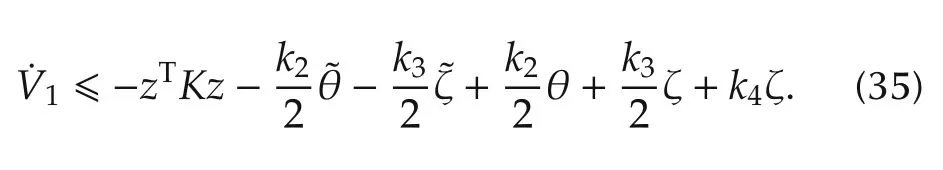
Let us denote

and rewrite(35)as

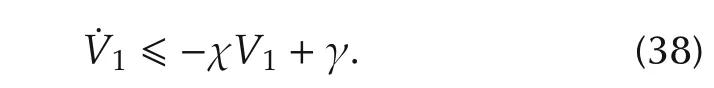
Multiplying(38)by eχt,yields

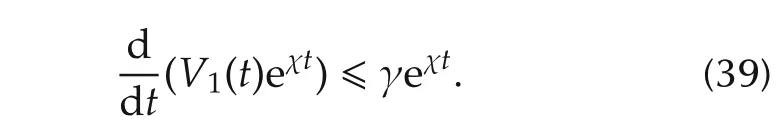
Integrating both size of the above inequality,we have

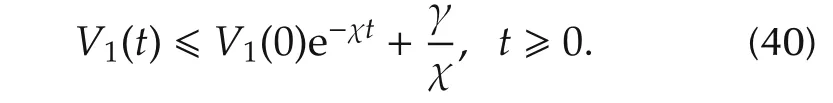
2)We need to show thatris bounded.From(20)we have

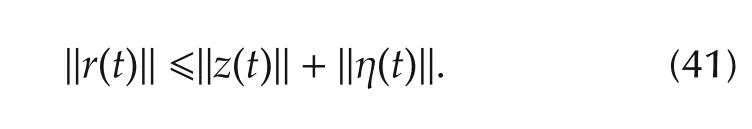
Using(40)with the denotation

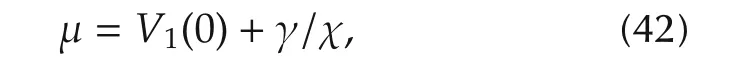
we obtain

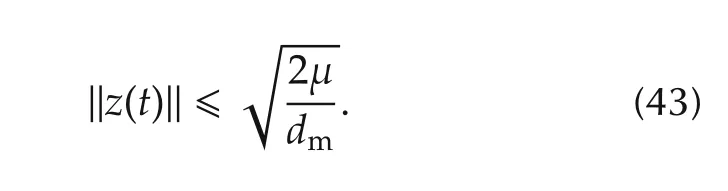
On the other hand,choosing η(0)=0 for(16)w e obtain the bound ofrfrom Lemma 1 as

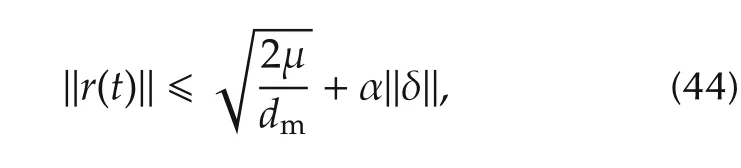
where

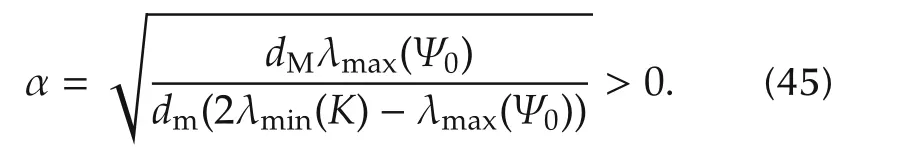
Having the bound ofrin(44),we show thatpand˙pare bounded as follows.From(5)we have

Solving(46),we obtain

Using(44),p(t)is bounded by

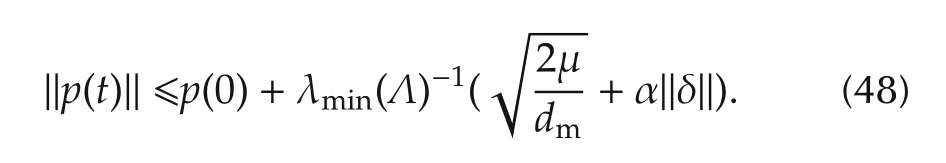
Consequently,from(46)the bound of˙pis

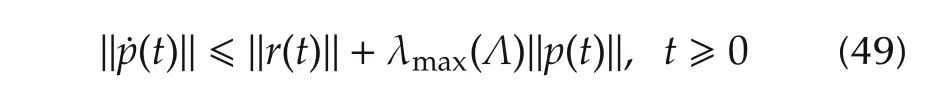
or

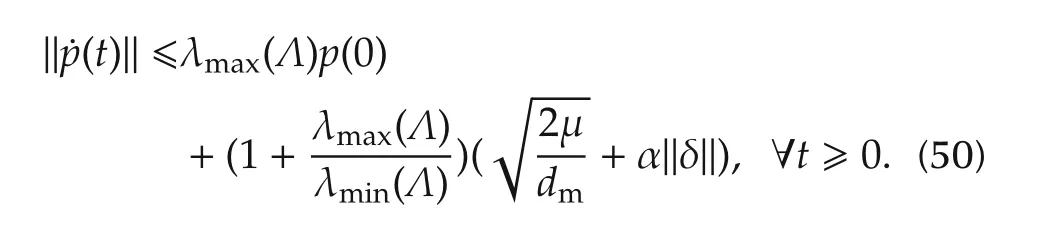
Thus,(44),(48)and(50)show that all the signals in the closed-loop system are bounded.Furthermore,from(29),(44),(47)and(49)we have

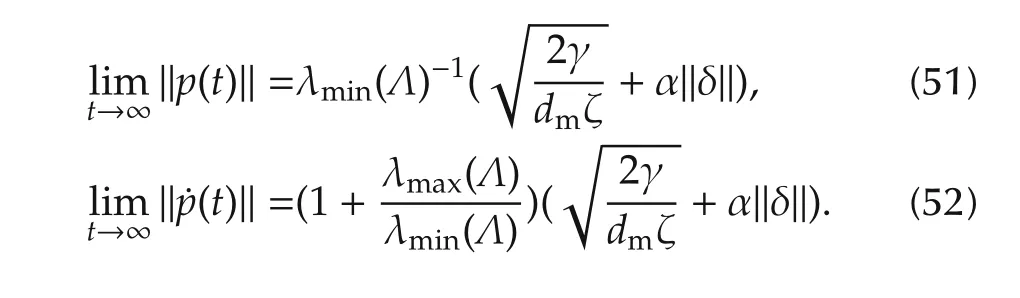
Thusp(t)and˙p(t)converge to the sets Ω1and Ω2defined as(30)and(31),respectively.□

Rem ark 1The com pact sets Ω1and Ω2in(30)and(31),respectively,still depend on Ψ0and δ.In practice,the matrix Ψ0may be chosen as identity matrixI.The bound¯uiof the control is needed to be large enough.Since,the large¯ui,fori=1,...,n,implies the small δ,and hence the small Ω1and Ω2as w ell.Clearly,freeuresults in δ=0,thenpand˙pcan be made arbitrarily small by choosing small γ in(37).

Rem ark 2In comparison with the existing work[8],the proposed control in this paper handles the situation of unknown input scalings Ψ in different direction.Namely,we consider the error ΨΔbetween the uncertain and nominal values of input scalings as a bounded disturbance.Then,the non-regressor approach is used to deal with this disturbance as w ell as bounded external disturbances.Furthermore,the proposed control here also differs from the control design in[27,Chapter 11].

4 Simulation results

To illustrate the effectiveness of the proposed control,we carry out the simulation on a Planar Elbow Manipulator with two revolute joints as depicted in Fig.1(see[16,Example 2.1]).The dynamics of the manipulator are described by

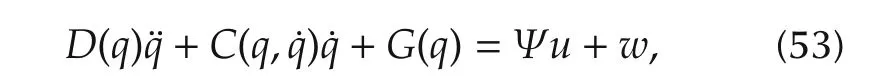
where

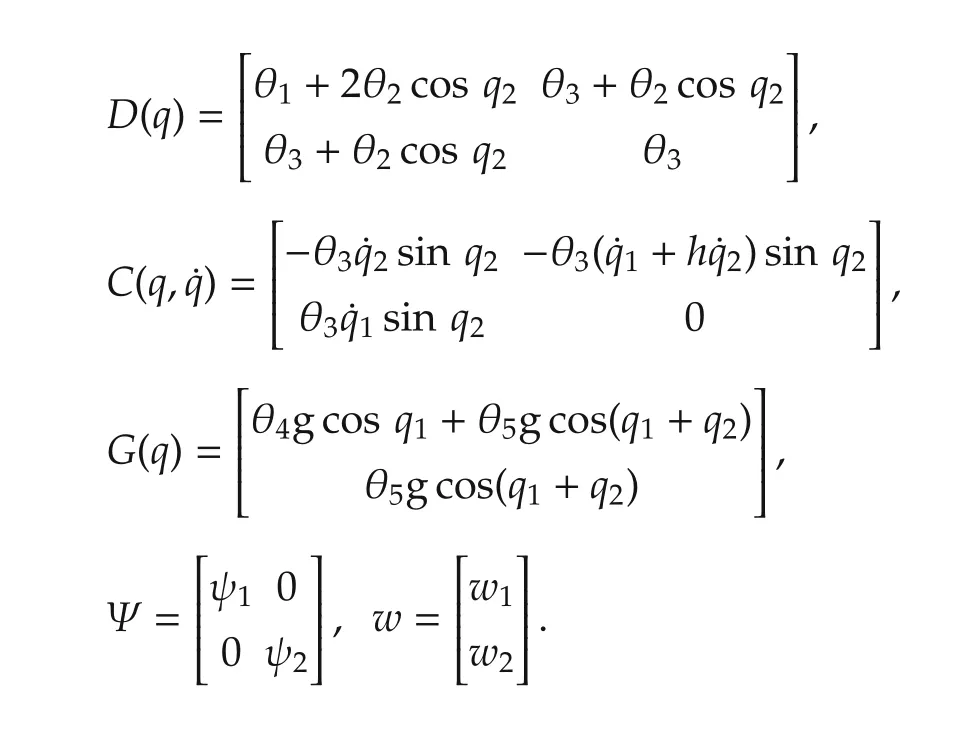
andis the vector of uncertain parameters.Moreover,from(8)the matrixY(q,˙q,ω)∈R2×5has the form of(54).The values of the parameters used in the simulation are given in Table 1.

The general expression for the desired trajectory is[8]

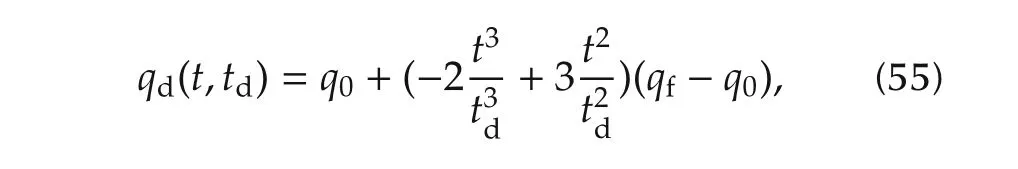
w hereq0andqfare the initial and final positions,andtdis the time at which the desired arm trajectory reaches the desired final position.

Fig.1 The Planar Elbow Manipulator with two revolute joints.

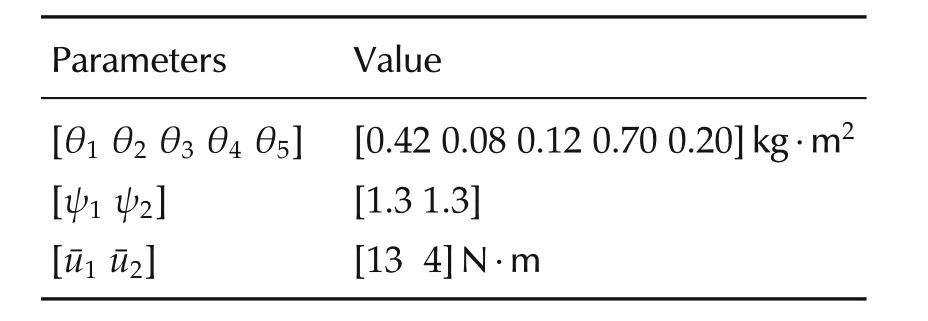
Table 1 The parameters of the planar elbow manipulator.

In the simulation,the following values are chosen:q(0)=[0 0]Trad,˙q(0)=[0 0]Trad/s,td=1s,qd(0)=[0 0]Trad,qd(td)=[1 2]Trad,ˆθ(0)=[0.21 0.04 0.06 0.35 0.10]Tkg·m2,Ψ0=d iag{1,1},Λ=d iag{1,1},K=d iag{15,3},Γ=d iag{0.2,0.2}.The control parameters are set as:k1=1,k2=0.03,k3=5,ρ=3,b=2,ε=2/(Φ+0.1).For(53),wgets the random values in[−0.01 0.01].For the model reference(16),we assumeD0(q)=0.75D(q)andC0(q,˙q)=0.75C(q,˙q).

For the comparison,we carry out the simulations of our proposed controller and the controller[28]with assuming exact input scalings and saturations.Fig.2 illustrates the positionsq1andq2while the angular velocities ˙q1and˙q2are depicted in Fig.3.The controlsu1andu2are shown in Fig.4.We can see that the tracking performance can be obtained well by proposed controller,while the static errors and big tracking errors appear under the controller with saturating the control inputs.The estimations of uncertain parameters are illustrated in Fig.5.The filtered tracking errorrand the auxiliary state η are shown in Fig.6.

Fig.2 Positions q1 and q2.

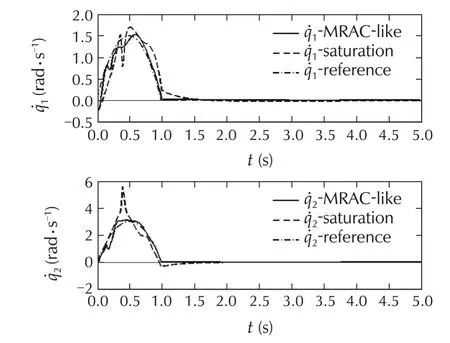
Fig.3 Angular velocities˙q1 and˙q2.

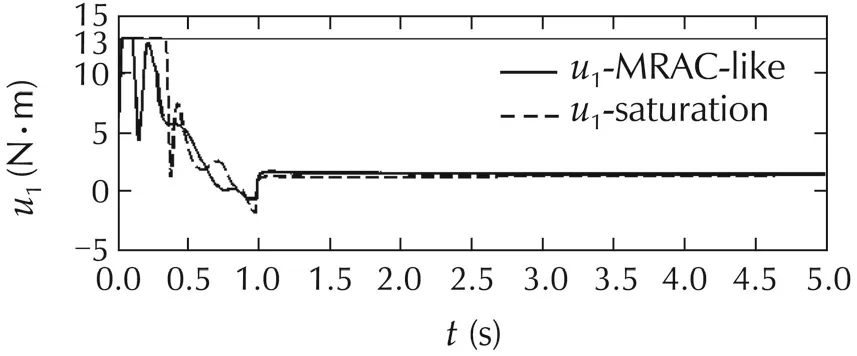
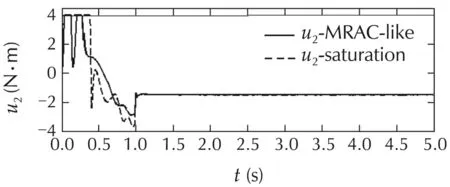
Fig.4 Controls u1 and u2.

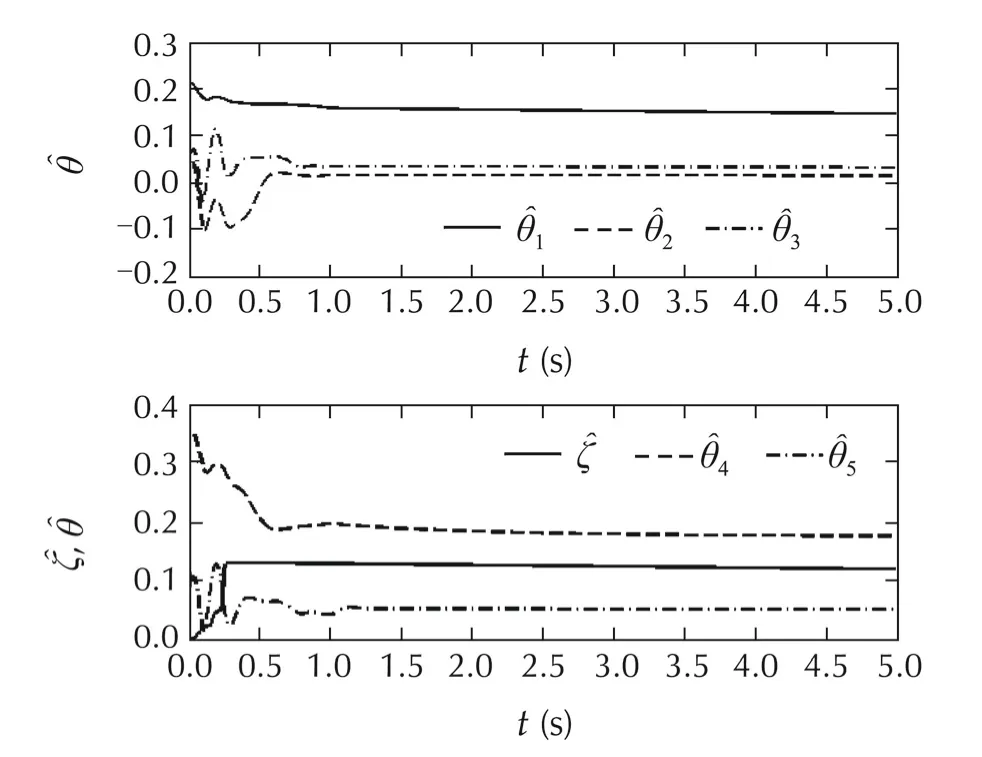
Fig.5 Estimations of and

Fig.6 The filtered velocity tracking error r and the auxiliary state η.

5 Conclusions

We have proposed the solution for the uncertain robotic manipulator with input saturations,unknown input scalings and external disturbances.Firstly,the uncertain dynamics of robot are handled by the use of the known function regressor.Second ly,we introduced the MRAC-like to deal with the input saturations.Fi-nally,the unknown input scalings and external disturbances were rejected by the non-regressor approach.In the results,the controller satisfied the input saturations,and achieved the convergence of the tracking errors to the region which depends on the input saturations.The simulation shows that the control objectives were completed.The future work is to design an output feedback controller for such robotic manipulator.

References

[1]F.L.Lew is,D.M.Daw son,C.T.Abdallah.Robot Manipulator Control:Theory and Practice.2nd ed.New York:Marcel Dekker Inc.,2004.

[2]M.W.Spong,S.Hutchinson,M.Vidyasagar.Robot Modeling and Control.New York:John W iley&Sons,2005.

[3]W.He,S.S.Ge,B.V.E.How,et al.Robust adaptive boundary control of a flexible marine riser with vessel dynamics.Automatica,2011,47(4):722–732.

[4]W.He,S.S.Ge,Y.N.Li,et al.Neural network control of a rehabilitation robot by state and output feedback.Journal of Intelligent&Robotic System s,2015,80(1):15–31.

[5]W.He,S.Zhang,S.S.Ge.Robust adaptive control of a thruster assisted position mooring system.Automatica,2014,50(7):1843–1851.

[6]H.Berghuis,R.O rtega,H.Nijmeijer.A robust adaptive robot controller.IEEE Transactions on Robotics and Autom ation,1993,9(6):825–830.

[7]E.V.Panteley,A.A.Stotsky.Adaptive trajectory/force control scheme for constrained robot manipulators.International Journal of Adaptive Control and Signal Processing,1993,7(6):489–496.

[8]S.S.Ge.Adaptive control of robots having both dynamical parameter uncertainties and unknown input scalings.Mechatronics,1996,6(5):557–569.

[9]T.T.Tran,S.S.Ge,W.He.Adaptive control for a robotic manipulator with uncertainties and input saturations.IEEE International Conference on Mechatronics and Automation(ICMA),Beijing:IEEE,2015:1525–1530.

[10]M.W.Spong,J.S.Thorp,J.M.Kleinwaks.The control of robot manipulators with bounded input.IEEE Transactions on Automatic Control,1986,31(6):483–490.

[11]W.E.Dixon,M.S.De Queiroz,F.Zhang,et al.Tracking control of robot manipulators with bounded torque inputs.Robotica,1999,17(2):121–129.

[12]A.Lor´ıa,H.Nijmeijer.Bounded output feedback tracking control of fully actuated Euler-Lagrange system s.System s&Control Letters,1998,33(3):151–161.

[13]A.Zavala-R´ıo,V.Santib´a˜nez.Simple extensions of the pd-with-gravity-compensation control law for robot manipulators with bounded inputs.IEEE Transactions on Control System s Technology,2006,14(5):958–965.

[14]P.K.Khosla,T.Kanade.Parameter identification of robot dynamics.Proceedings of the 24th IEEE Conference on Decision and Control,Fort Lauderdale:IEEE,1985:1754–1760.

[15]C.H.An,C.G.Atkeson,J.M.Hollerbach.Estimation of inertial parameters of rigid body links of manipulators.Proceedings of the 24th IEEE Conference on Decision and Control,Fort Lauderdale:IEEE,1985:990–995.

[16]M.W.Spong,R.Ortega.On adaptive inverse dynamics control of rigid robots.IEEE Transactions on Automatic Control,1990,35(1):92–95.

[17]J.J.E.Slotine,W.Li.On the adaptive control of robot manipulators.The International Journal of Robotics Research,1987,6(3):49–59.

[18]R.Kelly,R.Carelli,R.Ortega.Adaptive motion control design of robot manipulators:an input-output approach.International Journal of Contro l,1989,50(6):2563–2581.

[19]M.Krstic,I.Kanellakopoulos,P.Kokotovic.Nonlinear and Adaptive Control design.New York:John Wiley&Sons,1995.

[20]S.S.Ge,C.C.Hang,T.H.Lee,et al.Stable Adaptive Neural Network Control.1st ed.Berlin:Springer,2001.

[21]W.He,S.S.Ge.Robust adaptive boundary control of a vibrating string under unknown time-varying disturbance.IEEE Transactions on Control System s Technology,2012,20(1):48–58.

[22]W.He,S.S.Ge,B.V.E.How,et al.dynamics and Control of Mechanical System s in Offshore Engineering.London:Springer,2014.

[23]Y.D.Song.Adaptive motion tracking control of robot manipulators non-regressor based approach.International Journal of Control,1996,63(1):41–54.

[24]W.E.Dixon.Adaptive regulation of amplitude limited robot manipulators with uncertain kinematics and dynamics.IEEE Transactions on Automatic Control,2007,52(3):488–493.

[25]D.J.L´opez-Araujo,A.Zavala-R´ıo,V.Santib´a˜nez,et al.Output-feedback adaptive control for the global regulation of robot manipulators with bounded inputs.International Journal of Control,Automation and System s,2013,11(1):105–115.

[26]R.Ortega,M.W.Spong.Adaptive motion control of rigid robots:A tutorial.Automatica,1989,25(6):877–888.

[27]J.Zhou,C.Y.Wen.Adaptive Backstepping Control of Uncertain System s,Nonsmooth Nonlinearities,Interactions of Tim e-Variations.Berlin:Springer,2008.

[28]N.Sadegh,R.Horowitz.Stability and robustness analysis of a class of adaptive controllers for robotic manipulators.The International Journal of Robotics Research,1990,9(3):74–92.

[29]H.K.Khalil.Nonlinear System s.3rd ed.Upper Saddle River:Prentice Hall,2002.