利用光电效应原理估算孤立带电金属球上的电荷数量

刘雪芹，李登仟

(重庆理工大学 光电信息学院，重庆　400054)



利用光电效应原理估算孤立带电金属球上的电荷数量

刘雪芹，李登仟

(重庆理工大学 光电信息学院，重庆400054)

摘要：介绍了带电金属板所产生的光电效应，探讨了在一定温度下，将带电金属板的光电效应理论应用于孤立的带电金属球上求解其所含电荷个数。因为存在涨落和误差，该计算方法为近似处理。此外，还运用计算结果结合光电效应讨论其对尖端放电的影响。

关键词：孤立金属球；电荷；电子；光电效应；电容

赫兹于1887年在做电磁波实验时发现了光电效应现象。1905年，爱因斯坦受普朗克启发，提出“确实，在我看来，关于‘黑体辐射’、光致发光、紫外光产生阴极射线，以及其他一些有关光的发射和转化的现象的观察，如果用光的能量在空间中不是连续地分布的这种假说来解释，似乎就更容易理解”[1]的观点，进而假设光的量子性，成功解释了光电效应，并于1906年3月将光电效应理论推广至带电金属板的光电效应理论。这篇带电金属板的光电效应理论的论文《论光的产生和吸收》于当年发表在德国的《物理学杂志》[2]。

1905年，爱因斯坦在对光电效应进行解释时，做了“电子只吸收一个光子”的假设，仅停留在研究单光子吸收的问题。1929年，德国科学家玛利亚估计：当光子密度不低于每秒每平方厘米1024时，可能会产生双光子或多光子吸收现象[3]。之后，人们在光电效应方面的研究越来越多，光电效应广泛用于工业、军事领域。高科技军事产品之一的夜视器材就是光电效应的典范[4]。本文主要探讨一个带电金属球所含的电荷个数，并研究如何根据带电金属板的光电效应理论来求解带电金属球的电势。

1带电金属板的光电效应

1906年3月，爱因斯坦发现了光电散射和伏打之间可预期的定量关系，而定量关系的发现又伴随着带电金属板的光电效应理论[5](一种推广的光电效应理论)的提出。

带电金属板的光电效应理论大致可描述为：让金属板带正电荷，金属板就会与空气之间形成电势差即电压U。如果用光照射使其上面的电子逸出，至少要克服电势U的功。这是对该理论的定性描述。关于带电金属板更详细的介绍可参看相关文献。如果将带电金属板产生的光电效应转化成数学语言，可表述为

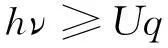
(1)

或

这里，忽略了电子的热运动(初动能)和逸出功w两项，在第2节中将对其原因做出理论解释。式(1)表明：如果忽略电子的热运动和其逸出功，只要光量子的能量超过Uq，光电子就可从金属中逸出。

设想有2块不同的带电金属板A1、A2，即使不用电压表也可以测量出这2块带电金属板之间的电压。用ν1、ν2分别表示这2块不同金属板对应的能引起光电效应产生的最小频率，那么有

(2)

根据式(2)不难看出：只要清楚能引起2块金属板产生光电效应的最小频率就可以计算出这2块金属板之间的电压。有趣的是，可以利用这个原理去测量极其微小的电压甚至超高电压值(在不考虑金属板被击穿之前)，因而带电金属板的光电效应理论的提出为新型电压表的研发提供了一定的理论依据。

目前看来，带电金属板产生的光电效应理论非常简洁，但其蕴含的物理规律却相对复杂。这里介绍带电金属板产生的光电效应为接下来计算带电金属球所含正电荷个数提供了依据。

2为什么忽略电子的初动能和逸出功

量子理论认为，金属中的自由电子可看作“电子气体”模型，电子气体的能量分布服从费米—狄拉克统计。量子力学认为，金属的逸出功应为

(3)

其中：χ为位能势能；EF为费米能量，见图1。

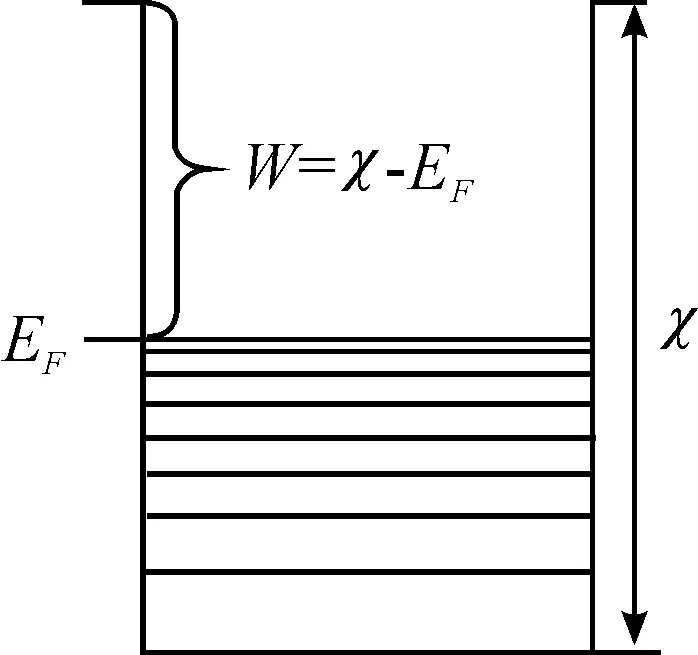
图1　电子逸出功示意图

按量子理论，逸出功是指处在费米能级上电子的能量与其在真空中距金属表面无穷远处的能量之差，即逸出功是电子逸出金属表面需要做的最小功[2]。根据爱因斯坦的光电效应方程

(4)

其中：ν、υ分别为光子的频率、光电子逸出速度，即逸出功是电子逸出金属表面所需做的最小功，这就意味着式(4)可改为

(5)

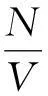
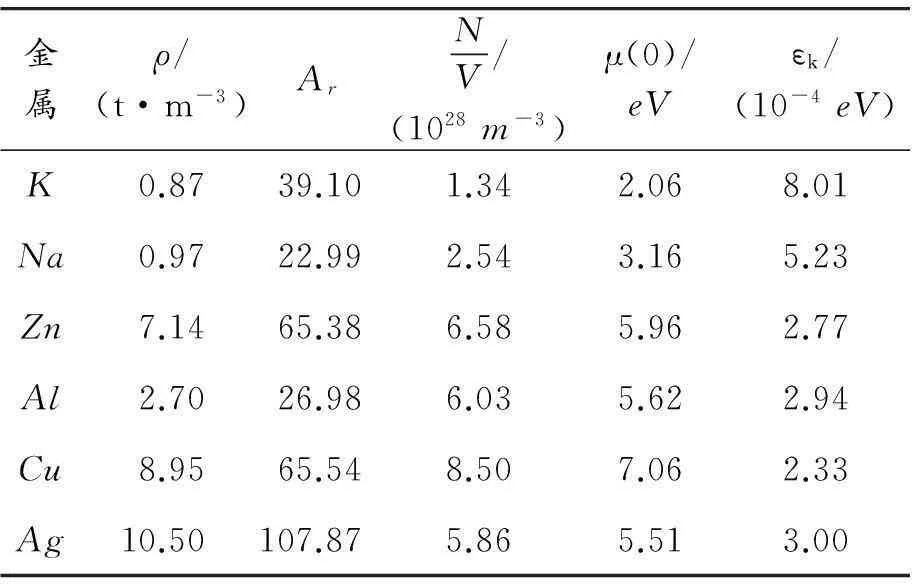
表1　 几种常见金属的电子热运动参量

在第1节中忽略了电子本身的逸出功，但爱因斯坦在文献中并没有给出解释，本文将对此作出一定的解释。

在一块带正电的金属板上，净正电荷产生的电势U为

(6)

这是一个电荷所产生的电势，带电金属板上的所有净正电荷n所激发的电势应为

(7)

这样，带电金属板上的所有净正电荷n对1个电子在Ri处产生的束缚功为

(8)

由于净正电荷只分布在金属板表面，这里认为所有的净正电荷与空气层的距离均为Ri>R≈Re，Re为电子轨道的经典半径。对Uq的值做一个大致的估计，取R>Re=10-10m(为简化计算，在数量级上做了近似处理)，则

(9)

根据式(9)，如果想把Uq的值和电子本身的逸出功w(一般为1 eV,有时甚至更高，不同金属板逸出功数量级基本相同，这里取近似估算值w=1 eV)作比较，并使其远大于电子的本身逸出功w，则必须使得式(9)中的值2.3×10-18·n远大于w=1 eV=1.602×10-19J，即n≫0.07,从而使得Uq≫w。因此，爱因斯坦在对带电金属板的光电效应方程做近似处理时，应认为带电金属板上的净电子数量n≫0.07，才可以把电子本身逸出功w忽略掉。事实上，带电金属板上的净正电荷的个数n≫0.07是可以满足的，且具有普遍性。至于带电金属板上带的是净正电荷或净负电荷则并不重要，由于电荷上的对称性以及所研究问题只和电性相关，从而上述表述对带电金属板带净负电荷也成立。

3带电金属球所含电荷的个数

设想有一个孤立(这样就可以避免击穿电压的影响)的半径为R的金属球，从四面八方往上面打带正的电荷。计算这个孤立的半径为R的带电金属球(以下简称带电金属球)所含的带正电荷的个数。

一个半径为R的孤立导体球的电容为[6]

(10)

如果假设带电金属球上面的带正的电荷个数为n，那么存在

(11)

由式(10)和(11)得

(12)

可见，如果知道了带电金属球所含电荷个数n时的电压值，就可以计算出此时n值的大小。由第1节介绍的带电金属板所产生的光电效应可知：能引起带电金属板产生光电效应的光子的最小频率为

(13)

事实上，不管是带电金属板还是带电金属球，上式都应成立。为了求出在带电金属球上面含有n个带正电荷时的电压，可以将一定频率的光子打在此时所对应的金属球上面，则总能找到能引起带电金属球产生光电效应的光子的最小频率v0，即为此时带电金属球表面的电势U。于是将式(13)代入式(12)可得

(14)

式(14)即为带电金属球所含带正电荷的个数。可见，如果测得该带电金属球的半径R和此时能引起带电金属球产生光电效应的光子的最小频率v0，就能够测得此时带电金属球上所带电荷的数量。

以上研究的是1个带电金属球所含带正的电荷的个数，而我们更想知道一个带电金属球所含电子个数的多少。由于电荷上的对称性，以及所研究对象和电荷的质量无关，因而式(14)不仅对带正的电荷是适用的，对电子仍然适用。事实上，式(14)只在趋于绝对零度下才近似成立，因为式(13)是在趋于绝对零度才严格成立，并没有考虑电荷的初动能在其中的作用。

在上面的讨论中，仅讨论了趋于绝对零度下一个带电金属球所含电子(电荷)个数的情况，而本文希望求得一定温度(带电金属球能保持固态的温度)下带电金属球所含电子个数的情况。

文献[5]表明：带电金属板完整的光电效应方程为

(15)

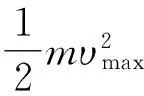
(16)

将式(16)代入式(14)，求得

(17)

文献[5]还表明：光电子在逸出金属板前后的动能减去外界提供的正或负的能量是一常数，称为光电子的净能量守恒方程，其数学表述为

(18)

将式(16)和(17)整理可得

(19)

其中C常数代表常数，它只和电子所处的初始状态有关。式(19)就是所求的结果，即一般温度下一个带电金属球所含电子个数的计算公式。也就是说，如果能测得在某一状态下1个带电金属球的温度T和带电金属球上电子的状态常数C常数，那么就可以算得此时带电金属球所含电子的个数。

尽管找到了可以计算带电金属球上所含电荷个数的计算方法，但应注意的是：以上计算方法仍存在一些缺陷，因为宏观的带电金属球上所带的电荷必然很多，由于存在涨落，式(19)的计算方法只能是一种近似。

4光电效应对尖端放电的影响

导体尖端的电荷分布特别密集，尖端附近的电场很强时就会发生尖端放电。作为一个很好近似处理，可以把一个导体的尖端的最尖锐部分看作很小的球，这样就可以利用式(19)来讨论光对尖端放电的影响。

尖端放电在实际生活中有着重要的应用，尤其是在避雷针方面。在尖端放电实验中，如果带电的尖端曲率越大，那么所产生的电场也越大，数学表述为

(20)

根据式(20)，要使得尖端放电的效应越明显，就要使尖端的电荷面密度σe越大，从而使得电场强度更强。大致说来，在一个孤立导体上，电荷面密度的大小与表面的曲率有关，导体表面曲率大的地方，电荷面密度较大；导体表面曲率小的地方，电荷面密度较小。但应注意，孤立导体表面的电荷密度σe与曲率之间并不存在单一的函数关系[6]。

4.1光照对带正电荷的尖端的影响

假设有一尖端导体，带正电荷。如果将此尖端放到周围都是空气的黑暗环境中，那么只要尖端上的电荷足够密集，就能产生足够大的电场，也就能发生尖端放电。而如果此时对尖端给予一定频率的光照,若能使得电子恰好逸出，那么必然满足方程

(21)

由于导体带正电，电子从上面逸出更加困难，因而所给予的光照频率要比平时使用不带电金属板打出电子的频率高得多(在这里不做具体讨论)。如果尖端带正电荷，那么一旦给予一定频率的光照，就会跑出更多的电子，也就使得尖端所带的正电荷更多，以至于尖端的面密度σe变大。因而，给予能使电子逸出的频率光照，将会使尖端放电的效应加强。光照的频率越高，尖端放电加强效应越明显。

4.2光照对带负电荷的尖端的影响

同上，使得尖端带负电荷，将其放置在同等环境下，若尖端可以发生尖端放电，给予一定频率的光照，且电子能从尖端刚好逸出，那么必然满足

(22)

对尖端带正电荷，当尖端带负电荷时，给予同等频率的光照(同4.1节中能使电子从带正电荷的尖端刚好逸出的光照)，那么根据式(22)，由于存在库仑力，净余负电荷产生的电场会把电子向外推，电子的逸出将会更加容易。但是随着光照的不断进行，尖端上的负电荷不断减少，以至于尖端放电现象会停下来，随着光照的进行，尖端上的负电荷减少至零，然后又开始出现正电荷，直到出现新的尖端放电现象，从而回到4.1节的“光照对带正电荷的尖端的影响”的讨论上面。

因而，对于初始带负电荷的尖端来说，随着一定频率光的照射，尖端放电现象将会减弱至零，然后随着尖端上正电荷的增多，尖端放电现象开始产生进而逐渐加强。

5结束语

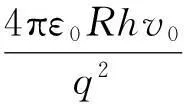
参考文献：

[1]约翰·施塔赫尔.爱因斯坦奇迹年[M].范岱年，许良英，译.上海：上海世纪出版社，2007:146.

[2]爱因斯坦.爱因斯坦文集(第2卷)[M].范岱年,许良英,赵中立,编译.北京:商务印书馆,2007:143.

[3]李莉，彭振生.对光电效应方程的再认识[J].宿州学院学报，2007,22(4)：93-94.

[4]霍连利，蒙上阳，杨秀清.光电效应实验分析[J].物理实验，2001,21(2)：41.

[5]李登仟.带电金属板所产生的光电效应及其分析[J].大学物理,2015，34(8)：54-57.

[6]赵凯华，陈熙谋.电磁学[M].北京：高等教育出版社，2013:109.

[7]方俊鑫,陆栋.固体物理学:下册[M].上海:上海科学技术出版社,1981:101-102.

(责任编辑杨黎丽)

Estimation of Number of Charges on Isolated Charged Metal Spheres Using Photoelectric Effect Thsory

LI Xue-qin， LI Deng-qian

(College of Optical and Electronic Information, Chongqing University of Technology,Chongqing 400054, China)

Abstract:The photoelectric effect of charged metal plate was introduced and the theory of the photoelectric effect was applied to calculate the charge number of the charged metal spheres. This method is approximation calculation because of fluctuation and error. In addition, the imfluence of the tip discharge was discussed by using the results and the photoelectric effect.

Key words:isolated metal ball; charge; electron; photoelectric effect; electronic capacitor

中图分类号：O422.1

文献标识码：A 1674-8425(2016)03-0116-05

doi:10.3969/j.issn.1674-8425(z).2016.03.020

作者简介：刘雪芹(1971—)，男，重庆人，博士，教授，主要从事新能源材料与器件研究；通讯作者 李登仟(1994—)，男，重庆人，主要从事新能源材料研究。

基金项目：重庆市基础与前沿研究计划项目(cstc2015jcyjA50033)

收稿日期：2015-10-10

引用格式：刘雪芹，李登仟.利用光电效应原理估算孤立带电金属球上的电荷数量[J].重庆理工大学学报(自然科学)，2016(3):116-120.

Citation format：LI Xue-qin，LI Deng-qian.Estimation of Number of Charges on Isolated Charged Metal Spheres Using Photoelectric Effect Thsory[J].Journal of Chongqing University of Technology(Natural Science)，2016(3):116-120.