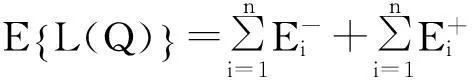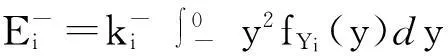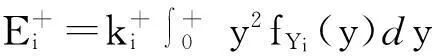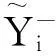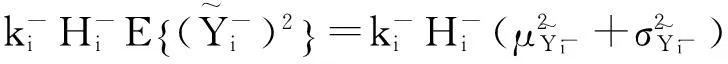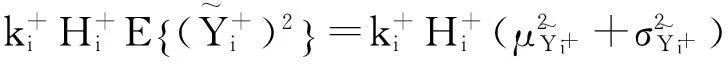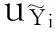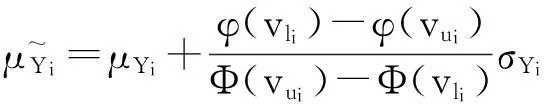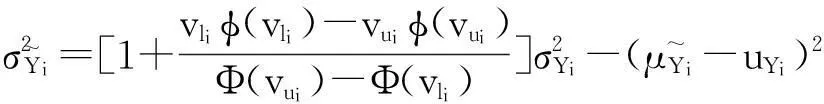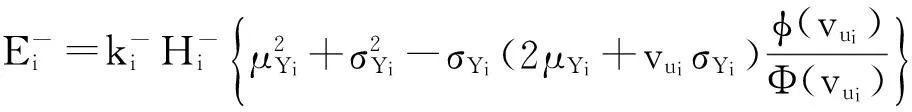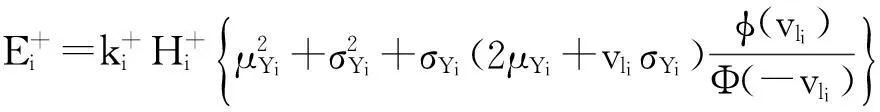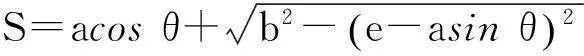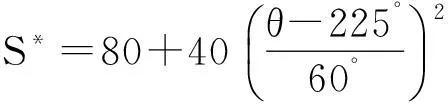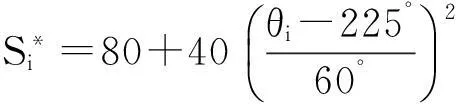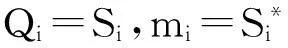基于非对称质量损失模型的函数机构稳健设计

杨昌明，段胜秋

(西华大学机械工程学院，四川 成都 610039)



基于非对称质量损失模型的函数机构稳健设计

杨昌明，段胜秋

(西华大学机械工程学院，四川 成都 610039)

摘要：为解决产品的质量特性偏离理想值所带来的非对称质量损失问题，提出一种非对称质量损失模型。应用截尾正态分布理论，推导出非对称质量损失的均值计算公式，以曲柄滑块机构为例，建立对称与非对称2种稳健优化模型。与对称质量损失函数相比，基于非对称质量损失函数的优化结果能够有效避开质量损失大的方向，从而有效减小质量损失。蒙特卡洛仿真实验验证了该方法的有效性。

关键词：稳健设计；非对称质量损失函数；曲柄滑块机构；蒙特卡洛法

在工程实践中，产品或工艺过程受到许多随机因素的影响，使得质量特性偏离目标，从而导致质量损失。文献[1]采用二次损失函数来表示这种损失的大小，该方法在工程应用中取得了明显的效果；然而，传统的二次损失函数是一种对称函数，但事实上产品的性能指标大于目标值和小于目标值所造成的损失可能是不对称的。例如，在孔类零件的加工中：当孔的实际尺寸小于孔的最小极限尺寸时，虽然属于不合格零件，但仍可以返工，这时质量损失相对小一些；当孔的实际尺寸超过孔的最大极限尺寸时，零件就要作废，则相应的质量损失就要大一些[2]。

平面函数机构在工程中应用广泛，减小运动误差、提高机构的运动精度及稳健性，有利于机构实现其预期功能。对此，学者们开展了这类问题的研究[3-5]，但从非对称质量特性的角度来开展机构稳健设计的研究还不多见。为此，本文提出一种非对称质量损失的稳健设计优化方法，并以曲柄滑块机构为例，进行理论计算和MCS验证。其结果表明，该方法可以减小质量损失，解决了质量特性较目标值偏大为好或偏小为好的稳健设计需求问题，有一定的应用价值。

1传统质量损失模型

产品质量特性受到随机因素的影响，当其偏离目标值时，就会引起质量损失。Taguchi提出的稳健设计，可以在不消除不确定性源的前提下，通过设计优化使影响因素对产品质量的影响尽可能小。

设影响因素分为可控因素X和不可控因素P，则质量特性Q可表示为

Q=f(X,P)。

(1)

设m为质量特性的目标值，则质量损失表示为

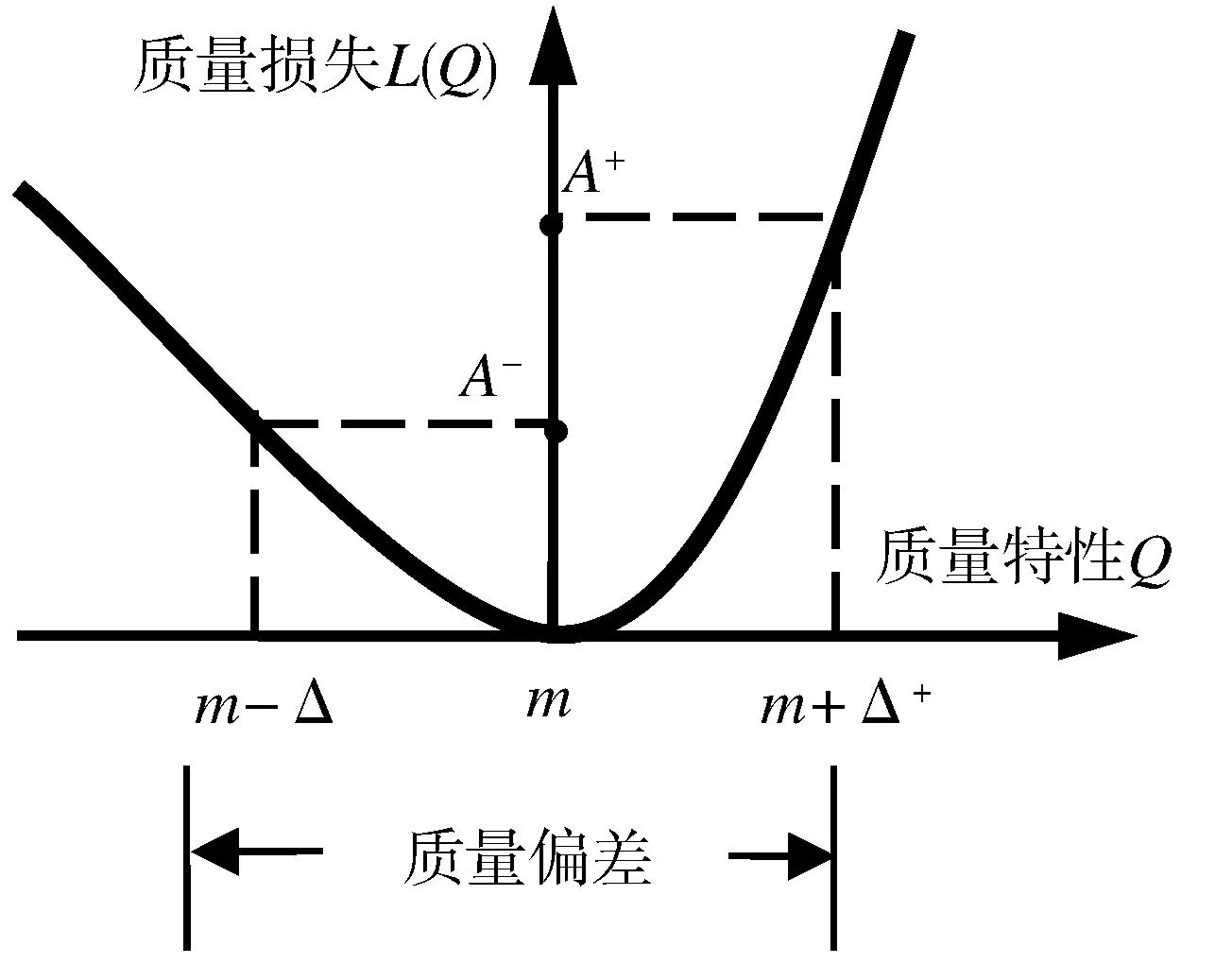
(2)

该函数曲线如图1所示。其中，Δ为质量特性的规定偏差，A为质量特性Q在点m-Δ或m+Δ处所对应的质量损失。

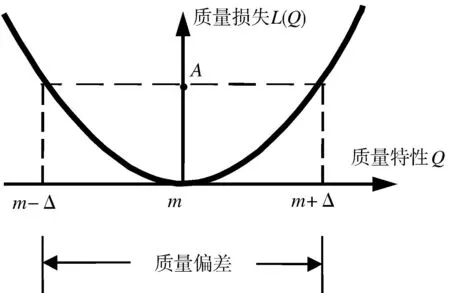
图1　对称质量损失函数

由于产品的质量特性是随机变量，所以质量损失函数也是随机的。令Y=Q-m，则Y的目标值为0，其质量损失的期望值E{L(Y)}可表示为

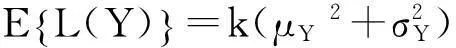
(3)

式中k=A/Δ2。

如果产品或工艺过程有n个质量特性，则有

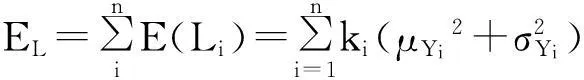
(4)

2非对称质量损失模型

传统的质量损失函数是对称的，但实际生产制造中，质量特性偏离目标造成的损失在很多情况下是非对称的。假设质量特性的规定偏差区间为[m-Δ-,m+Δ+]，A+是质量特性为m+Δ+时的质量损失，A-是质量特性为m-Δ-时的质量损失，质量损失函数为：

(5)

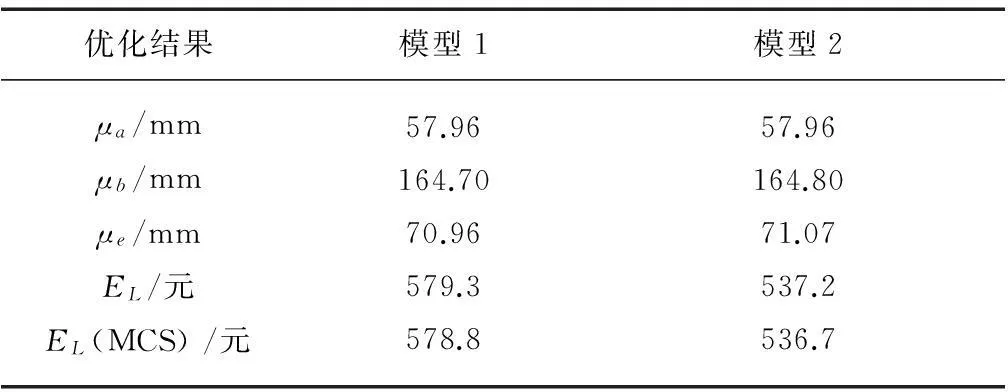
当A->A+时，其质量损失函数如图2所示。

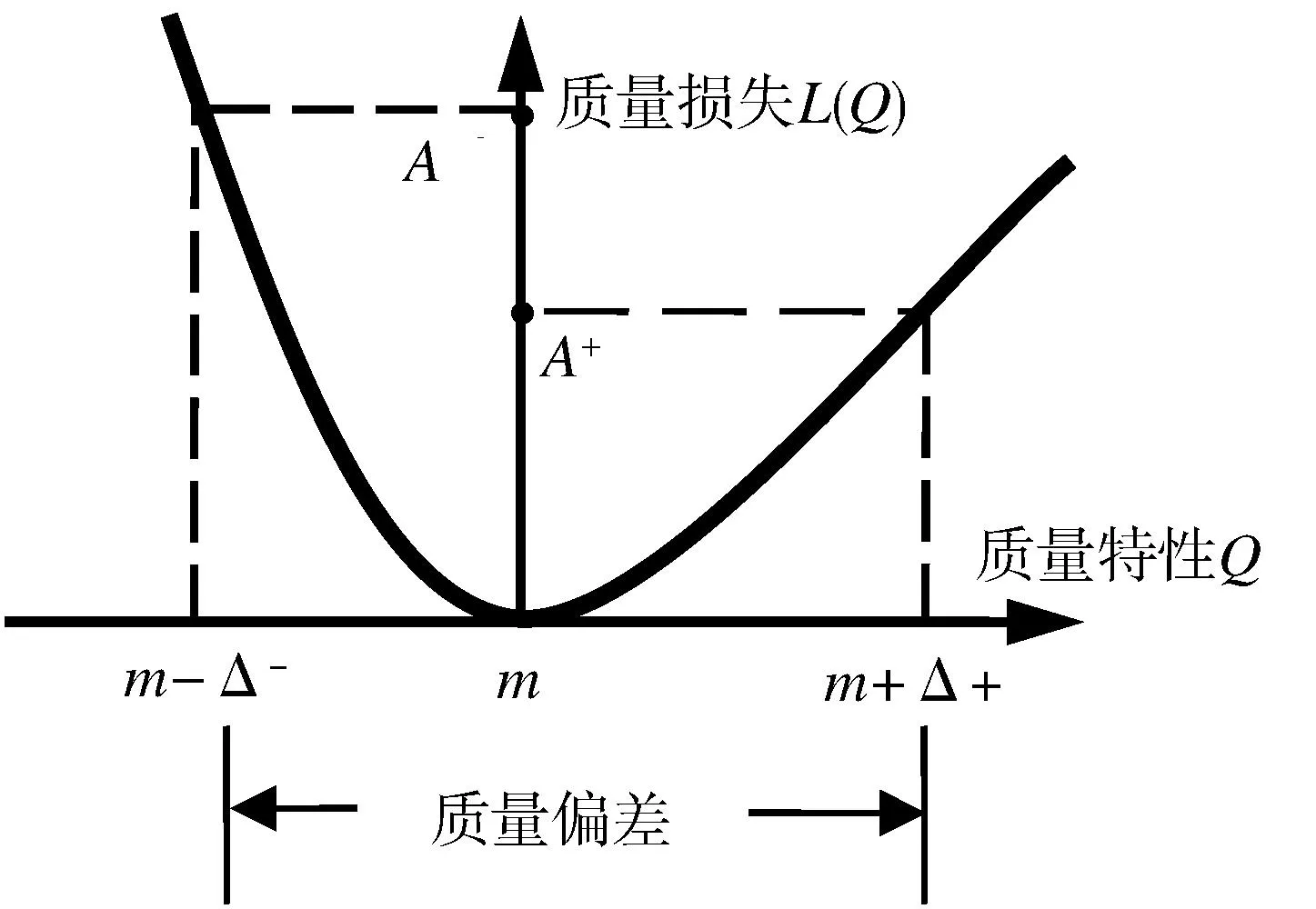
图2　非对称质量损失函数(A-> A+ )

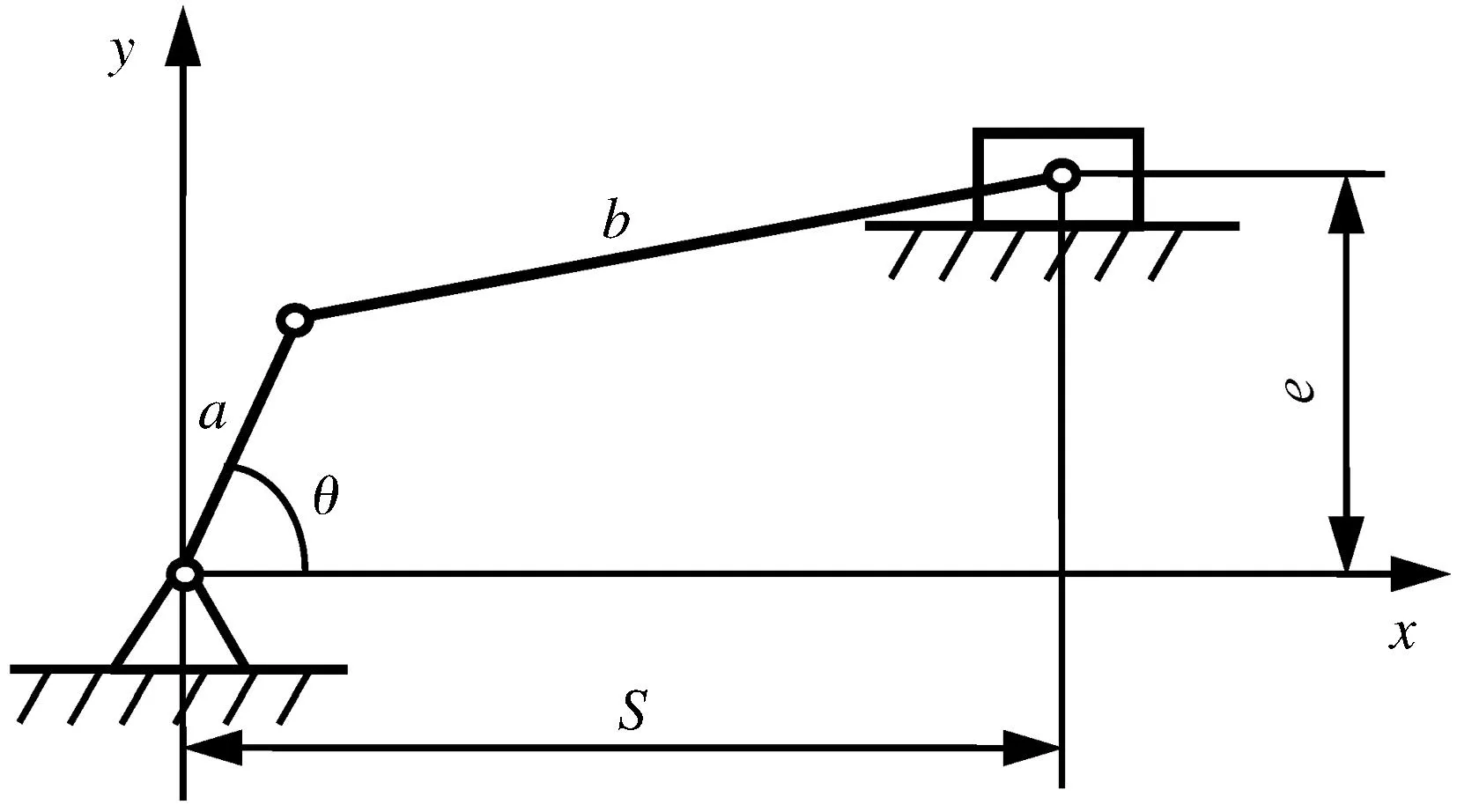
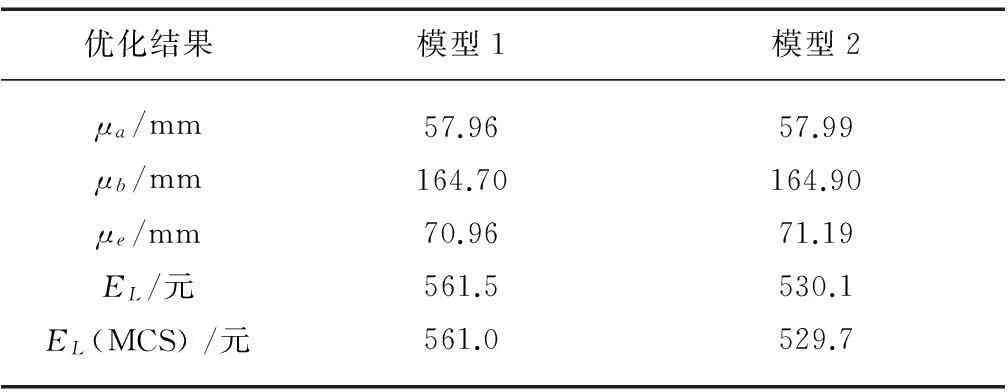
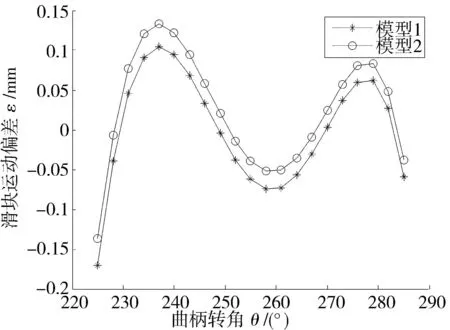
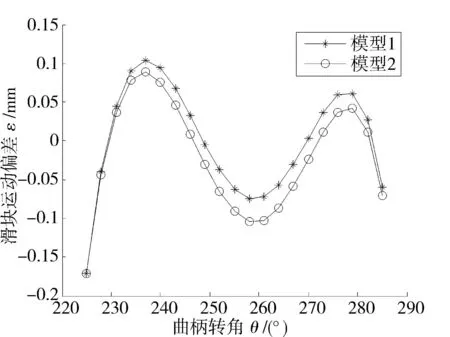
反之，当A-

图3　非对称质量损失函数(A-< A+)

此时，由于质量损失函数不是关于m对称的，所以将其截尾为[-,m]和[m,+]2部分，质量损失函数的期望E{L(Q)}则为

(6)

令Yi=Qi-mi，则新的目标值为0，因此有：

(7)

(8)

式中fYi(y)～N(μYi,σYi)。

(9)

同理，式(8)可变化为

(10)

(11)

(12)

在目标值为0的情况下，对0点左边的质量特性而言，由于其截尾分布范围为[-,0]，可知vli=-，vui=-μYi/σYi。由φ(-)=0，Φ(-)=0，根据式(9)、(11)和(12)，可得

(13)

(14)

3曲柄滑块机构误差分析

曲柄滑块机构是常见平面函数机构，如图4所示，a为曲柄长度，b为连杆长度，e为滑块偏置距离，θ为曲柄转角。曲柄滑块机构的实际运动规律为

(15)

在曲柄滑块机构设计时，给定S*为已知的运动规律，则滑块的运动误差为

ε=S-S*=f(a,b,e,θ)。

(16)

图4　曲柄滑块机构

ε为滑块实际运动规律与设计目标之间的偏差，其理想值为0。由式(16)可知，ε是关于a、b、e、θ的函数，而且由于加工误差等原因将导致a、b、e的波动，也就将导致ε的波动，降低了运动精度的可靠性及稳健性。

按稳健设计的思想，当实际值S偏离理想值S*时，将产生质量损失，而且某些情况下S大于和小于S*所带来的损失大小是不对称的。例如活塞在气缸中的运动情况，在上止点、下止点处出现正的运动误差，有利于排气与做功。

4曲柄滑块机构算例

针对图4所示的曲柄滑块机构，机构需要实现的运动规律如式(17)所示函数：

(17)

将曲柄的工作转角范围[225°，285°]离散为21点，则：

θi=225°+(i-1)×3°(i=1,2,…,21)；

(18)

(19)

根据式(4)建立传统稳健设计优化模型1，为：

(20)

式中：[μa，μb，μe]为随机变量X=[a，b，e]的均值；g=e+a-b≤0表示曲柄存在条件，与质量特性一样，该约束函数也同样受到随机因素的影响，采用罚函数方法施加概率约束；μg,σg分别为g的均值与标准差；β可根据实际情况取值，本算例β=4。

根据式(6)、(13)、(14)建立非对称稳健设计优化模型2，为：

(21)

假设随机变量服从正态分布，且[σa,σb,σe]=[0.025, 0.025, 0.025]，取k-=A-/Δ2= 400/0.32，k+=A+/Δ2= 200/0.32。对于非对称情况，k-=2k+；对称情况则取k=k+。2种模型对应的优化结果如表1所示。

表1　优化结果(A-> A+)

令k-=A-/Δ2= 200/0.32，k+=A+/Δ2= 400/0.32。对于非对称情况，k+=2k-；对称情况则取k=k-。2种模型对应的优化结果如表2所示。

表2　优化结果(A+> A-)

采用蒙特卡洛方法(MCS)进行验证，抽样次数为106，结果见表1和表2，仿真与理论计算的损失(按费用比较)非常接近，说明本文算法有很高的计算精度。

图5　滑块运动偏差(A- > A+)

由图5可知，当A->A+时，为了避免质量特性偏小方向的大质量损失，所以较模型1，模型2将点往质量特性偏大方向移动。当A+>A-时，质量特性偏大方向的质量损失大于偏小方向，所以模型2各点较模型1向偏小方向移动，见图6。从表1与表2可知，当涉及质量特性偏好时，采用非对称质量损失模型可以获得更小的质量损失。可见，相对于对称质量损失函数，非对称质量损失函数可以很好解决Y偏大为好还是Y偏小为好的质量特性设计优化需求问题。

图6　滑块运动偏差(A+> A-)

5结论

1)工程实际中，大于或小于理想值所带来的损失是不同的，为此，本文提出一种非对称质量损失函数及其参数估计算法，无需数值积分。通过蒙特卡洛仿真验证，其误差很小，计算精度高，表明该方法有效。

2)以曲柄滑块机构为例，建立了传统质量损失函数模型与非对称质量损失函数模型。其验证结果表明，非对称质量损失模型的结果能够有效避开质量损失大的一方，使得质量损失变小。

3)提出的方法很好地解决了质量特性较目标值偏大为好或偏小为好的稳健设计需求问题，有一定的应用价值。

参考文献

[1]Taguchi G,Elsayed E A, Hsiang T C. Quality Engineering in Production System [M]. New York:McGraw-Hill, 1989:45-56.

[2]陈湘来, 韩之俊, 张斌. 非对称损失函数的质量特性值优化选择[J]. 工业工程, 2008,11(3):24.

[3]李奇, 张均富. 平面轨迹机构的静态综合可靠性分析[J].西华大学学报(自然科学版)，2015，34(3)：17.

[4]陈胜军, 贾方, 韩伟. 曲柄滑块机构运动误差分析[J]. 机械设计与制造, 2015(3):72.

[5]庞欢, 喻天翔, 宋笔锋. 平面连杆机构运动精度可靠性及灵敏度分析[J]. 中国机械工程, 2014,25(18):2415.

[6]Du Xiaoping.Robust Design Optimization with Bivariate Quality Characteristics[J]. Structural and Multidisciplinary Optimization,2012,46(2):187.

(编校：饶莉)

Robust Synthesis of Function Mechanisms by Using Asymmetric Quality Loss Models

YANG Changming， DUAN Shengqiu

(SchoolofMechanicalEngineering，XihuaUniversity,Chengdu610039China)

Abstract:In order to account for asymmetric quality loss problems resulted from quality characteristics deviation to targets, we propose asymmetric loss models. Firstly, truncated normal distribution theory is applied to computing the expected value for asymmetric loss functions. Symmetric and asymmetric optimization models are then built for robust synthesis of a slider-crank mechanism. Compared with symmetric quality loss model, asymmetric quality loss model has the advantage to shift away from big quality loss and reduce quality loss. Finally, the Monte Carlo simulation solutions show that the proposed approach is effective in robust design for problems with asymmetric quality losses.

Keywords:robust design; asymmetric quality loss function; slider-crank mechanism; MCS

doi:10.3969/j.issn.1673-159X.2016.02.006

中图分类号：TH112

文献标志码：A

文章编号：1673-159X(2016)02-0030-4

基金项目：教育部重点实验室资助项目流体及动力机械(SBZDPY-11-22)。

收稿日期：2015-11-16

第一作者：杨昌明(1969—)，男，教授，博士，主要研究方向为数值仿真、稳健设计等。E-mail:cmyang@163.com

·机电工程·