随机市场下保险公司最优投资策略:期望效用最大化

黄冬冬，吴 杰，陈传钟

（海南师范大学 数学与统计学院，海南 海口 571158）

随机市场下保险公司最优投资策略:期望效用最大化

黄冬冬，吴 杰，陈传钟*

（海南师范大学 数学与统计学院，海南 海口 571158）

文章研究了保险公司在随机市场下风险过程为Lévy过程且资本可以投资到风险资产和无风险资产，应用鞅方法对二次效用函数得到均值—方差有效投资问题的显示解.

均值-方差有效投资组合；向前向后随机微分方程；跳扩散过程；鞅方法

最优投资组合选择问题一直是金融市场学者研究的重点.Perera［1］（2010）研究了在Lévy市场状态转换模型下投资者带可保风险的最优消费、投资和保险策略.Sotomayor［2］（2009）求得了体制转换模型下最优消费投资问题的显示解.Wang［3］（2007）用鞅方法研究标准Black-Scholes模型下保险公司的最优投资.Zhou［4］（2004）运用Markowitz均值-方差选择连续时间市场状态转换模型的投资组合.Bin［5］（2014）于2014年研究了市场为带跳扩散过程模型下HARA效用函数最优投资和风险控制策略.本文在随机市场下考虑保险公司最优投资问题的均值-方差准则，应用鞅方法得到二次效用函数最优投资策略的显示解.

1 模型

在时间段［0，T］上考虑仅有两种可交易资产的金融市场：一种是无风险资产如债券，其价格过程为Bt；另一种为风险资产如股票其价格过程为St.在概率空间（Ω，F，（Ft）0≤t≤T，P）上Bt和St满足如下随机微分方程rt，μt和σt为正的有界函数，为标准布朗运动.

保险公司的风险过程Rt为

假定索赔额Y=｛Yi，i≥1｝为独立同分布的随机变量序列，累计分布函数F满足F（0）=0，且扩散项表示在保险公司t时刻不确定的剩余是一种二维布朗运动使得分支的相关系数为ρ.可以表示为为另一标准布朗运动独立于W（1）.

进一步假设W（1），W（2），N和｛Yi，i≥1｝为相互独立.若Lt表示补偿泊松过程为F的均值，则风险过程（3）可以表示为

令c=α-λmF则

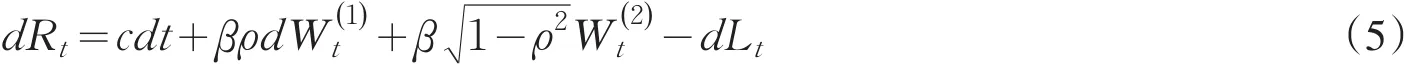
这里c和β为常数，W（1）和W（2）为两个独立的布朗运动，L为一维纯跳Levy过程.它们都是定义在（Ω，F，（Ft），P）上，（Ft）由（W（1），W（2），L）生成且F=FT.W（1），W（2）和L相互独立.设u表示L的跳的测度.它的对偶可料投影v的形式v（dt，dx）=dt×m（dx），m（｛0｝）=0且我们假设Levy测度m如下：

（A1）∫Rx2m（dx）＜∞

在假设（A1）下，Lt为平方可积且由Levy分解为（Cont and Tankov（2003））

注1：对风险模型（3），m（dx）=λF（dx）.

保险公司允许将资金投资到股票和债券上.交易策略可以表示为（Ft）-可料过程π=πt，πt表示在t时刻投资到股票的资产.

所有容许交易策略组成的集合记为Π.相对于容许交易策略π和初始资本x0，保险公司的财富过程Xx0，π满足如下随机微分方程

即

假设保险公司最终财富的效用函数为U，则其目标为

效用函数U为严格凹，且在（-∞，∞）上连续可导.因为U为严格凹，则对保险公司来说至多存在唯一的最优终端财富［8］.

对任意π*∈Π和π∈Π，由U的凹性可以得到

由式（10）我们可以得到如下性质，给出了最优交易策略的充分条件.

性质1 若存在一策略π*∈Π使得在为常数，则π*为最优交易策略.

引理1 对任意P-鞅Z，存在可料过程θ=（θ1，θ2，θ3）使得对所有有［10］

2 均值-方差准则

均值-方差投资组合的选择问题是在π∈Π上最大化期望终端财富且同时最小化终端财富的方差.这是带有两个相矛盾准则的多目标最优化问题.若不存在交易策略π∈Π使得这两个不等式至少有一个严格成立，则交易策略π*∈Π称为均值—方差有效.我们知道寻找均值—方差有效策略等价于最大化期望二次效用.下面对问题（9）考虑二次效用函数

2.1 有效策略

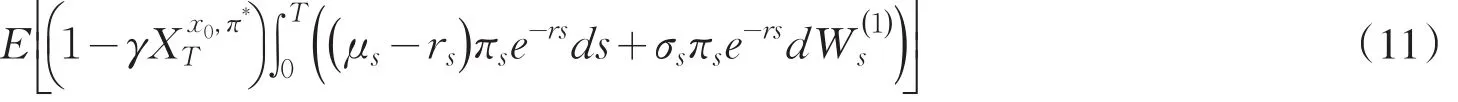
为常数.

引理2 设π*∈Π，则π*满足条件（11）当且仅当存在使得为下面向前-向后随机微分方程（FBSDE）的解.

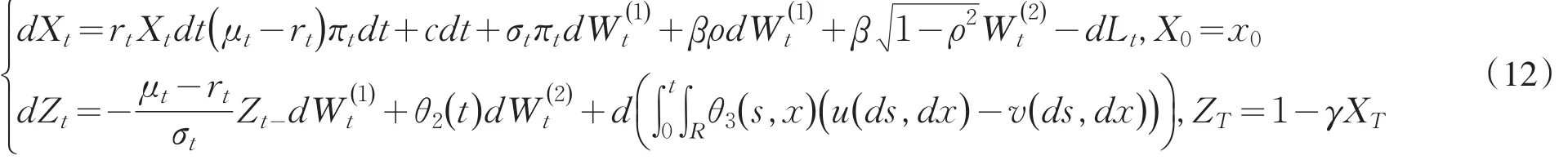
式（12）中P为由左连续（Ft）-适应过程生成的σ-代数表示为所有关于（Ft）-适应过程（Xt）且满足的集合，L2（P）为所有关于（Ft）-可料的实值过程θ1满足的集合为所有定义在可测实值函数θ3使得对所，为局部可积递增过程，这里

证明 假设π*满足条件（11）.Xx0，π*∈L2F为（12）中FBSDE的解为一平方可积鞅.对任意停时τ≤ T，设，则πτ∈Π.将πτ代入（11），对所有停时τ≤T，

为常数.这说明

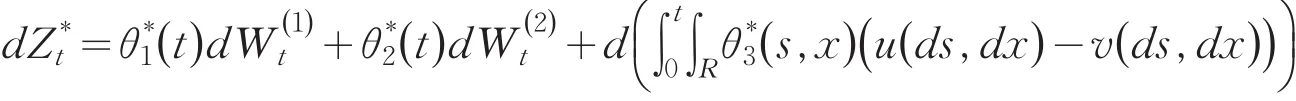
由Ito公式可得

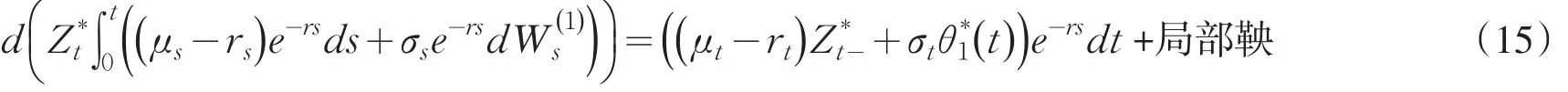
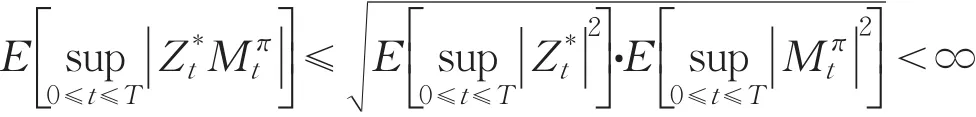
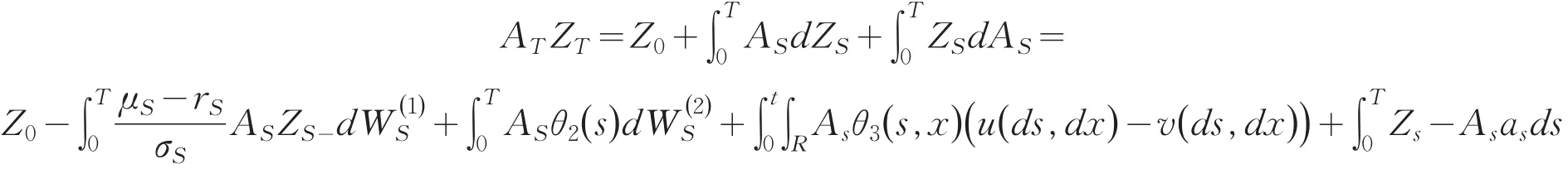
则

设（X，π，Z，θ2，θ3）为FBSDE（12）的解，则必然有分别比较（19）式和（8）式的和 d（u-v）项，可以猜测有

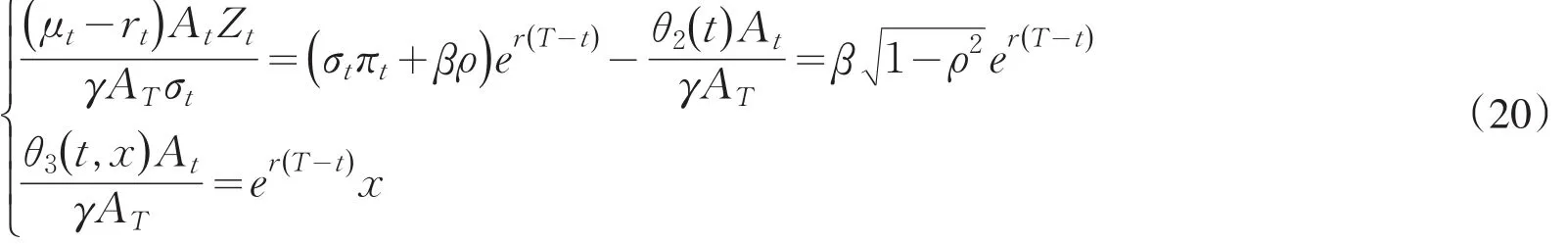
即

将（21）式代入（19）式，且等式（8）我们有

若取

且

下面我们验证上面的猜想.设

且

则SDE

会有解［12］

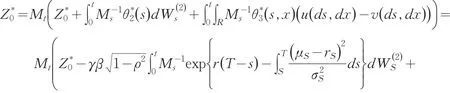
这里

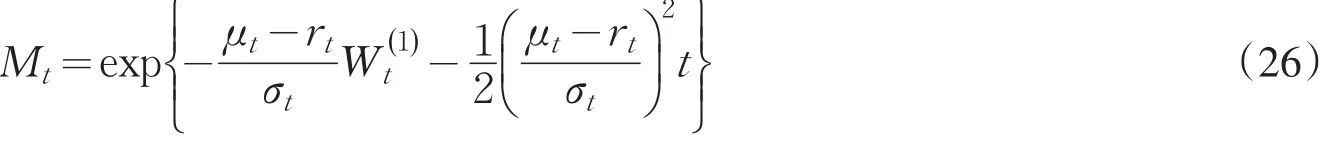
令

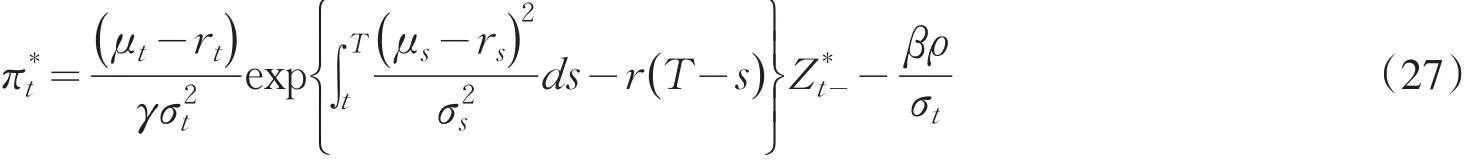
最后由性质1和引理2结合上面的结论我们有如下定理

定理1 设π*定义为由（24）—（27）形式，则π*为二次效用函数的最优交易策略.

3 结论

本文研究了保险公司在随机市场下风险过程为Lévy过程且资本可以投资到风险资产和无风险资产，通过选择投资策略来最大化终端财富的期望效用.应用鞅方法对二次效用函数得到均值—方差有效投资问题的显示解，可以得出最优投资策略与市场的收益、风险及无风险利率有关，对实际的投资应用具有一定的理论指导意义.此外，还可以推广到其他效用函数如对数效用函数来研究最优投资问题的显示解.

［1］Perera R.Optimal consumption，investment and insurance with insurable risk for an investor in a Lévy market［J］.Insurance Mathematics and Economics，2010，46：497-484.

［2］Sotomayor L，Cadenillas A.Explicit solutions of consumption investment problems in financial market with regime switching［J］. Math，Finance，2009，19：251-279.

［3］Wang Z，Xia J，Zhang L.Optimal investment for an insurer：the martingale approach［J］.Insurance Mathematics and Economics，2007，40：322-334.

［4］Zhou X Y，Yin G.Markowitz’s mean-variance portfolio selection with regime switching：a continuous-time model［J］.SIAM J，Control optim，2004，42：1466-1482.

［5］Bin Z，Abel C.Optimal investment and risk control policies for an insurer：Expected utility maximization［J］.Insurance Mathematics and Economics，2014，58：57-67.

［6］Eun J J，Jai H K.Optimal investment strategies for the HARA utility under the constant elasticity of variance model［J］.Mathematics and Economics，2012，51：667-673.

［7］Zhuo J，Yin G，Wu F.Optimal reinsurance strategies in regime-switching jump diffusion models：stochastic differential game formulation and numerical methods［J］.Insurance Mathematics and Economics，2013，53：733-746.

［8］胡华，胡若.双曲绝对风险厌恶函数的最优消费与投资组合的显式解［J］.上海理工大学学报，2007，29（1）：42-44；78.

［9］张凌梅，徐伟.具有双曲绝对风险厌恶函数类投资者的风险度量［J］.西北工业大学学报，2006，24（6）：741-744.

［10］叶中行，林建忠.数理金融资产定价与金融决策理论［M］.北京：科学出版社，1998.

［11］严加安.金融数学引论［M］.2版.北京：科学出版社，2012.

［12］詹森，王辉丰.构造双偶数阶空间更完美幻立方的四步法［J］.海南师范大学学报：自然科学版，2014，27（4）：389-395.

责任编辑：刘 红

Optimal Investment Strategies for an Insurer in Stochastic Markets:Expected Utility Maximization

HUANG Dongdong，WU Jie，CHEN Chuanzhong*
（School of Mathematics and Statistics，Hainan Normal University，Haikou 571158，China）

In this paper we investigate mean-variance criterion of the optimal investment problem for an insurer.The insurer’s risk process is modeled by a Lévy process and the capital can be invested to the risky assert and the riskless assert. We obtain explicit solutions of the optimal investment strategy for the quadratic utility function by martingale approach.

Mean-variance efficient portfolio；Forward-backward stochastic differential equation（FBSDE）；Jump-diffusion process；Martingale approach

F 830

A

1674-4942（2016）02-0131-06

2016-02-27

国家自然科学基金（11361021）

*通讯作者