Hamming图H(D,q)与Hadamard乘法

付月敏

(河北师范大学 数学与信息科学学院,河北 石家庄　050024)



Hamming图H(D,q)与Hadamard乘法

付月敏

(河北师范大学 数学与信息科学学院,河北 石家庄050024)

摘要:本文给出了Hamming图H(D,q)的标准模上的一组基，并讨论了该基在 Hadamard乘法下的性质.

关键词:Hamming图； Hadamard乘法； 基

1预备知识

令Γ=(X,R)表示一个没有重边,没有环的无向有限连通图,其中X为顶点集,R为边集.令∂为Γ顶点之间的距离函数.记D:=max{∂(x,y)|x,y∈X},我们称D为Γ的直径.称Γ是距离正则的,如果对于任意整数h,i,j(0≤h,i,j≤D),任意顶点x,y∈X,当∂(x,y)=h时,数值

对于0≤i≤D,规定MatX(C)中矩阵Ai如下：

称Ai为Γ的第i个距离矩阵,矩阵A1称为Γ的邻接矩阵,简记为A.易知：

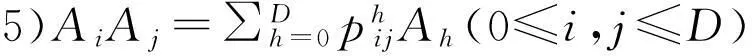
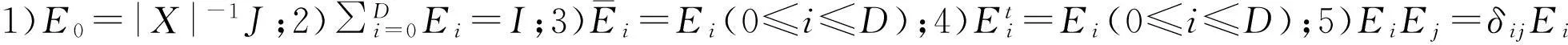
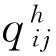
2完全图及其标准模上的Hadamard乘法

任意两个顶点都邻接的简单图称为完全图,具有n个顶点的完全图记为Kn.完全图是直径为2的距离正则图[1].令A为Kn=(X,R)的邻接矩阵,取定x∈X,A*=A*(x)为Kn的对偶邻接矩阵,V=CX为其标准模.则由E0=|X|-1J可知

A0=I,A=J-I=|X|E0-I.

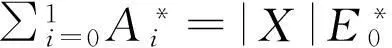
(1)

其中,

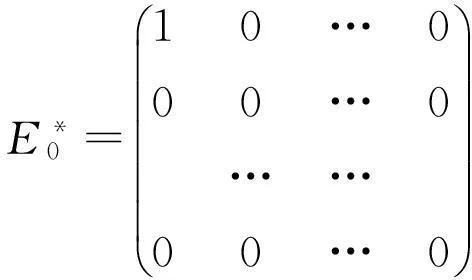
定义MatX(C)中矩阵Δ如下：

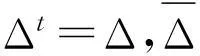
并且下式成立：

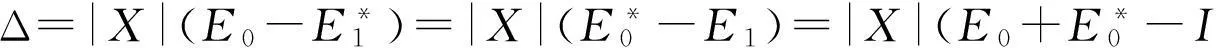
(2)

引理1符号如上所述,则有

1)AΔ=ΔA*;

2)A*Δ=ΔA.

证明： 由式(1),(2)可知

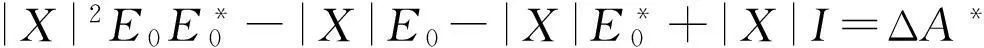
故1)式成立.同理2)式可证.

引理3设y∈X,且y≠x.则有

(3)

(4)

成立,其中Ⅱ为全1列向量.

证明： 由Δ的定义以及E0=n-1J和E0+E1=I事实结论可得.

引理4下面结论成立：

1)对于任意y∈X,且y≠x,有

(5)

2)对于不同的y,z∈X,且y,z≠x,且有

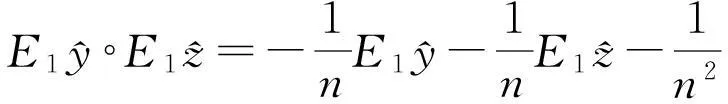
1)得证.同理2)可证.

引理5下面结论成立：

1)对于任意u∈V,

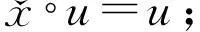
2)对于任意y∈X,且y≠x,有

3)对于不同的y,z∈X,且y,z≠x,有

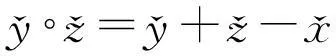
由(4)和(5)有

2)得证.同理3)可证.

3Hamming图及其标准模上的Hadamard乘法

定义1设Y是一个基数为q(q≥2)的有限集合,D为正整数,Hamming图H(D,q)的顶点集为X=YD.两个顶点相邻当且仅当这两个序列仅有一个位置上的元素不同.

定义2 设图Γ=(X,R)和图Γ′=(X′,R′),规定Γ×Γ′为顶点集合X×X′的图.顶点(u,v)与顶点(u′,v′)邻接当且仅当或者u=v且u′与v′在图Γ′中邻接,或者u′=v′且u与v在图Γ中邻接.我们称Γ×Γ′是Γ与Γ′的卡氏积.

定义3文献[6，p.404]对于任意B∈MatX′(C)和B′∈MatX′(C),规定B⊗B′为MatX×X′(C)中矩阵,且((u,u′),(v,v′)的值等于B的(u,v)值与B′的(u′,v′)值之积.我们称B⊗B′为B与B′与的张量积.

由文献[3,p.107]有

(B1⊗B1′)(B2⊗B2′)=(B1B2)(B1′B2′);

(6)

B⊗(γ1B1′+γ2B2′)=γ1B⊗B1′+γ2B⊗B2′;

(7)

(γ1B1′+γ2B2′)⊗B=γ1B1′⊗B+γ2B2′⊗B,

其中,γ1,γ2∈C.

引理6文献[6.p.404]Hamming图H(D,q)可以看做D个Kq的卡氏积,即Kq×Kq×…×Kq则H(D,q)的邻接矩阵A为

(8)

其中,I1为q×q的单位矩阵.H(D,q)的对偶邻接矩阵A*为

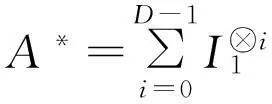
(9)

(10)

构成V的一组基.

定义4取定x∈X,规定MatX(C)中矩阵Δ为

(11)

由(6)可知Δ可逆,并且其逆元

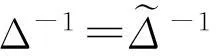
(12)

引理8符号如上所述,则有

1)AΔ=ΔA*;

2)A*Δ=ΔA.

证明： 由(7),(8)和(11)可知

由引理1,式(9),(7)和(11)可知上式为

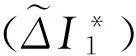
从而1)得证.同理2)可证.

对于任意y,z∈X,设

(13)

是其中两个元素,由(3.12)，(3.13)和引理7可知

对于任意y,z∈X,有

(14)

下面给出本文的主要结论.

定理1符号如上所述,下面结论成立：

1)对于任意u∈V,

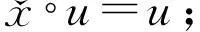
2)对于任意y∈Γ(x)有

3)对于不同的y,z∈Γ(x)有

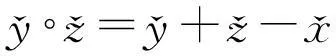
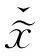
再由引理5知1)成立.

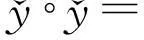
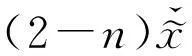
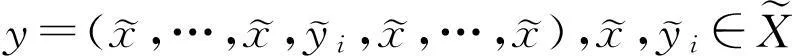
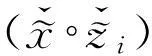
从而3)式成立.

参考文献：

[1]BrouwerA.E.,CohenA.M.andNeumaierA.Distance-RegularGraphs[M].Springer,Berlin,1989.

[2]冯克勤,章璞,李尚志.群与代数表示引论[M].合肥: 中国科学技术大学出版社,2006.

[3]EvesH.ElementaryMatrixTheory[M].AllynandBaconInc.,Boston,1966.

[4]BiggsN.AlgebraicGraphTheory[M].Secondedition,CambridgeUniversityPress,Cambridge,1993.

[5]TerwilligerP.Thesubconstituentalgebraofanassociationscheme,(PartI)[J].J.AlgebraCombin.,1992,1(4):363-388.

Hamming graphsH(D,q) and Hadamard multiplication

FU Yue-min

(CollegeofMathematicsandInformationScience,HebeiNormalUniversity,ShijiazhuangHebei050024，China)

Abstract:In this paper，we give a base |y∈X} for the standard module of Hamming graphs H(D,q),and discuss the properties of the base under the Hadamard multiplication.

Keywords:Hamming graphs;Hadamard multiplication; Base

中图分类号：O157.5

文献标识码：A

文章编号：1001-9383(2016)01-0001-06

作者简介:付月敏,女,河北人,硕士研究生,主要研究方向为代数与代数组合.

基金项目:河北省自然科学基金项目(A2013205021)

收稿日期：2016-02-17