基于SOTSFNN的溶解氧浓度控制方法
2016-05-11乔俊飞付文韬韩红桂北京工业大学电子信息与控制工程学院计算智能与智能系统北京市重点实验室北京100124
乔俊飞,付文韬,韩红桂(北京工业大学电子信息与控制工程学院,计算智能与智能系统北京市重点实验室, 北京 100124)
基于SOTSFNN的溶解氧浓度控制方法
乔俊飞,付文韬,韩红桂
(北京工业大学电子信息与控制工程学院,计算智能与智能系统北京市重点实验室, 北京 100124)
摘要:针对污水处理过程溶解氧浓度难以控制的问题,提出了一种基于自组织T-S模糊神经网络的控制方法。其实质是采用模糊规则层激活强度的方法,根据实际环境自适应的对神经元进行调整,构造合适的控制结构,从而提高控制精度。同时采用梯度下降法对控制器的各个参数进行实时调整。该控制器运用在污水处理基准仿真模型中进行实验,结果表明,提出的SO-TSFNN控制方法能够较好地实现对溶解氧浓度的控制,具有较好的自适应性。关键词:神经网络;控制;溶解氧浓度;动态仿真;自组织算法
2015-12-18收到初稿,2015-12-28收到修改稿。
联系人及第一作者:乔俊飞(1968—),男,博士,教授。
引 言
溶解氧浓度(DO)是污水处理过程中一个重要的控制参数,直接影响微生物的生长状况,从而进一步影响污水的处理效果,因此能否快速有效地将其控制在合理的范围之内是整个污水处理过程能否正常运行的前提[1]。由于污水处理过程具有非线性、干扰严重等特点,同时,DO容易受到进水等各组分浓度的影响,进而加大了对DO控制的难度[2-3]。针对DO控制这一问题,国内外的很多学者进行了大量研究,并提出了一系列的控制方法,取得了较好的控制效果。
Holenda等[4]将氧气传输系数KLa5作为操作变量,采用预测控制策略对DO进行控制,并将其保持在2 mg·L−1。Wahab等[5]将多变量PID控制器应用到污水处理过程中,实现对DO的控制,同时对PID控制器的各个参数进行了优化。Vrecko等[6]采用PI控制器与前馈控制策略相结合应用到污水处理过程中,实现了对DO浓度的控制。Liu等[7]将MPC模型预测控制方法与PID控制方法相结合,应用到BSM1中实现对污水处理的控制。
然而,针对PID控制器的控制参数的选择较为烦琐,需要大量的经验值;同时,PID控制虽然在理论和实际的应用中较为成熟,但普遍存在控制精度低的问题。将基于传统PID控制器的控制方法应用到污水处理过程这类的复杂非线性过程中,由于控制器本身特点的限制,难以在这类非线性系统中取得满意的控制效果[8-11]。学者们为了提高对非线性系统的控制精度及满意的控制效果,根据非线性系统的特点研究了大量智能控制方法,其中一些学者将其应用于污水处理过程中,在较大程度上提高了污水处理的控制效果和控制精度。目前,主要采用的是智能控制方法。
胡玉玲等[12]将模糊神经网络控制器应用在变参数活性污泥法中对DO进行控制,实验获得了良好的控制效果。Chandramouli等[13]将回流污泥量和氧气传输系数作为控制量,溶解氧浓度和底物浓度为被控量,进行了关于神经网络自适应控制的研究,取得了较好的效果。Belchior等[14]将一种自适应模糊控制策略引用到污水基准仿真平台(BSM1)中实现了对DO的控制。
大量研究结果表明,智能控制系统能够较好地适用于污水处理这类的非线性过程。然而由于固定结构的控制器,在控制这类具有不确定性等特点的非线性过程时很难达到理想的控制效果。当环境发生变化时,控制器很难针对当前环境变化进行相应的调整。所以研究一种能够根据环境变化自组织调整控制器结构的智能控制方法极为重要。Han等[15]将一种自组织RBF神经网络模型预测控制方法应用到BSM1中对DO进行控制,获得了良好的效果。由此可知自适应结构的控制器在复杂多变的环境下能够起到较好的控制作用。
文中针对污水处理过程中DO跟踪控制的问题进行了相关的研究,由于T-S模糊神经网络(TSFNN)可以通过模糊规则对先验知识进行表达,同时具有较强的学习、适应能力,以及较好的非线性映射能力。然而污水处理过程中具有多工况的情况,对TSFNN进行了相应改进,提出一种自组织T-S模糊神经网络(SOTSFNN)构建算法,利用其在线学习能力,强大的容错能力,以及自组织结构对环境的自适应性,实现对DO的实时控制[16]。最后将该算法应用到BSM1平台中,实验结果验证了该方法的可行性和有效性。
1 前置反硝化污水处理过程
欧盟科学技术合作组织(COST)和国际水协(IWAQ)合作开发,共同提出了BSM1基准仿真模型,BSM1的总体布局如图1所示。该模型为控制策略和方法的控制性能提供了一个验证平台。BSM1基准仿真模型主要包括两个部分如图1所示,由生化反应池和二沉池组成。生化反应池分为5个单元,前2个单元为缺氧区;后3个单元为好氧区。生化反应池采用的是IAWQ提出的ASM1数学模型进行模拟,数学模型中包括13种组分,8个生化反应过程及19个参数[17-18]。
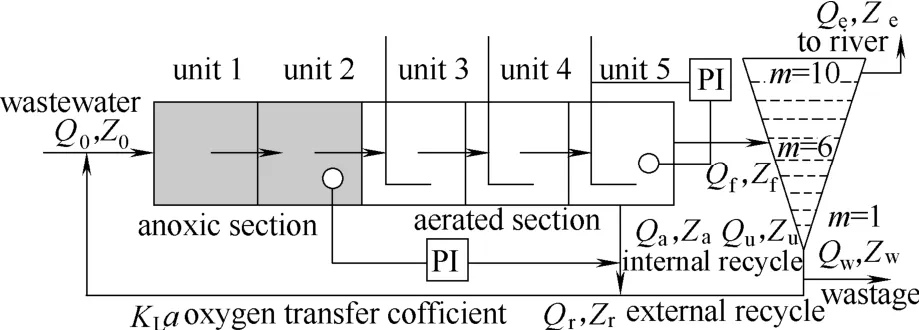
图1 前置污水处理反硝化工艺Fig.1 Structure of BSM1 baseline simulation model
研究表明,第5分区的DO直接关系到出水水质的组分浓度,对系统的脱氮具有决定性的影响。在基准仿真平台中,通过对对生化反应池中的第5分区KLa5的控制可以实现对DO的控制。
2 SOTSFNN控制器的设计
模糊神经网络是将神经网络与模糊逻辑系统相结合,综合了两者的优点[19]。一般情况下,模糊神经网络分为4层:第1层输入层,对系统进行信息的输入;第2层为模糊化层,对输入信息进行模糊化处理;第3层为模糊规则层,是通过模糊规则进行模糊逻辑推理;第4层为去模糊化层,将输出量去模糊化后,输入到被控对象中。
TSFNN被广泛应用于复杂的、非线性系统的控制中,被很多学者认为是最具有优势和潜力的一种模糊神经网络。由于TSFNN的后件部分主要采用线性函数的表现形式,与Mamdani模型等相比,TSFNN的输出是线性组合[20]。可以通过较少的模糊规则来包含更多的信息,从而能够更简单的实现非线性控制系统的。
2.1 TSFNN网络结构
TSFNN结构(固定结构为例)如图2所示。由前件网络和后件网络构成。前件网络用于模糊规则及模糊推理,后件网络则进行网络线性组合的输出。
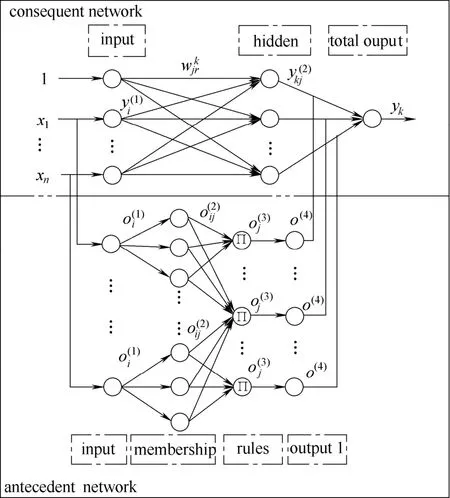
图2 TSFNN结构Fig.2 T-S fuzzy neural network structure
2.1.1 前件网络 输入层:位于该层的各神经元节点不做任何计算,而是将输入量直接引入T-S模糊神经网络的前件网络中。该层节点的输出就等于输入,即

隶属度层:隶属度函数采用的是高斯函数。
规则层:位于该层的的每个节点的输出可以表示为模糊规则的规则强度。
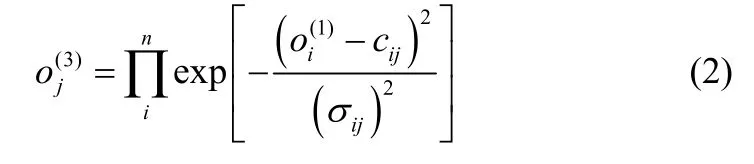
式中,cij和σij分别表示高斯函数的中心值和宽度值。
输出层:该层的主要作用是将上一次的输出去模糊化,输入到后件网络中。
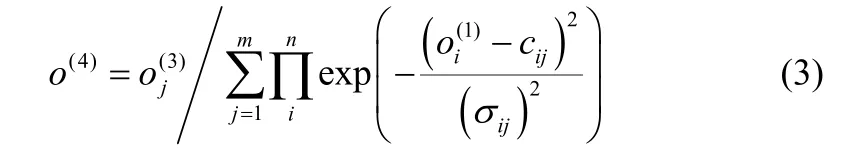
2.1.2 后件网络 输入层:将输入量直接引入TSFNN的后件网络中,进而将输入变量传送到隐含层。

隐含层:该层中的节点代表模糊规则的后件。
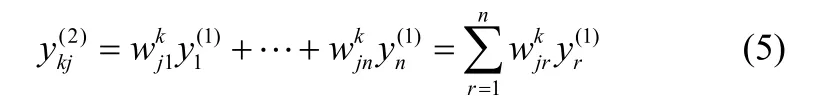
总输出层:计算TSFNN的总输出,即

式中,yk是后件网络各规则的加权和,也就是TSFNN的网络输出。o(4)为加权系数,即前件网络的输出,同时作为网络输出的连接权值。
2.2 自组织神经网络结构
传统的TSFNN网络采用凑试法选取模糊规则,得到固定不变的网络结构及规模[21]。然而将固定结构的TSFNN控制器用于复杂多变的环境中,很难达到理想的控制效果,所以设计一种能够根据环境改变而自适应调整控制结构的控制器至关重要。
所以,选择合适的模糊规则数对于整个模糊神经网络的性能尤为重要[22]。如果模糊规则数太多,会使系统的逻辑关系过于庞大,计算量呈指数级递增;如果模糊规则数太少,使得网络的表达性下降。通过式(2)的数学描述中可知,每一条模糊规则可以看作为一个类,而规则数的确定可以依靠输入输出决定,也就是说,模糊规则数等于类别数。
简单的聚类算法中,一般将第1组数据作为第1个类的中心。如果新进数据与某一已知聚类中心的距离小于设定的限值r,则说明该数据属于这一类;如果距离大于设定值,则将该数据作为一个新的聚类中心。根据这一思想,对新增模糊规则的初始化进行选择和调整。在初始状态下不包含过多的模糊规则,没有模糊规则。在系统运行过程中,将第1组数据作为第1个类的中心,从而产生第1条模糊规则。当系统选择增加模糊规则后,将该时刻的新入数据作为新一类的中心,从而达到对新模糊规则的初始化。
文中所采用的SOTSFNN网络结构是在TS模糊神经网络的基础上加入了激活强度的概念。激活强度主要表达的是模糊规则层的输出。激活强度的大小说明了该模糊规则在SOTSFNN中作用的程度。如果激活强度较大,则说明该模糊规则起到的作用越强,对整个系统的贡献也就越多;反之则说明作用较小,贡献也较小。通过对激活强度的判断和比较,能够更好的决定和提升整个网络的性能和规模。
模糊规则激活强度表达式如式(8)所示

式中,sj是模糊规则激活强度;xi是输入向量;cij是隶属度函数的中心;σij是隶属度函数的宽度。
从中选取现有规则中激活强度最强的一条规则,如式(9)所示
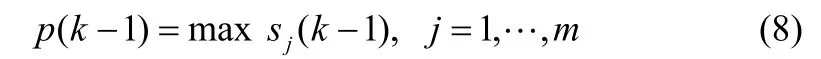
如果p( k− 1)> r,其中r∈(0,1),意味着该输入数据在已有的规则类别中存在与其近似的一类,则说明规则数不用增加,保持不变。同时,为了保证整个系统的稳定,需要对激活一类的中心值进行更新,如式(10)所示
式中,c(k)为更新中心值;N为该类的样本数;c( k− 1)为上一时刻的中心值;xk为当前时刻的输入样本。
如果p( k− 1)< r,则说明在已有类中无法找到能够与新入数据相匹配的一类,即现有的模糊规则无法满足环境的要求,需要新增一条模糊规则,也就是说,相对应的前件网络的隶属度层及后件网络的隐含层分别增加一个神经元,如图3所示。
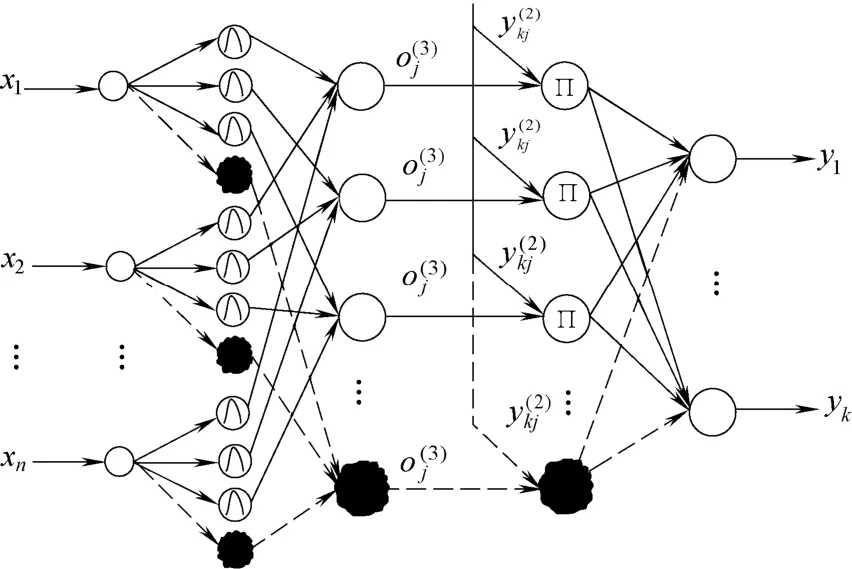
图3 SOTSFNN结构Fig.3 Structure of SOTSFNN
当增加一条新的模糊规则后,需要对该模糊规则中所属隶属度函数的中心值和宽度值及前件网络的权值进行初始化,如式(10)~式(12)所示。

式中,c(k)为新增隶属度函数中心值,将采集的输入数据作为新增模糊规则的中心;σ(k)为新增隶属度函数宽度;σ(k− 1)为与新入数据最小欧氏距离的中心的宽度值;w(k)为后件网络的权值,新增权值为系统初始第1条模糊规则学习后的权值。
对激活强度判断之后,SOTSFNN进行相应的计算,并通过梯度下降法对模糊规则的中心值、宽度值、权值以及学习率进行学习。
2.3 SOTSFNN的学习算法
SOTSFNN网络的学习算法采用梯度下降法对网络的中心值、宽度值、权值以及学习率进行调整。
定义1个目标函数
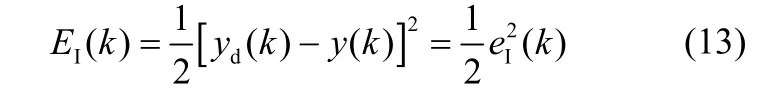
式中,EI(k)为每次迭代后的瞬时平方差,yd(k) 和y(k)分别表示为k时刻的期望输出和实际输出;eI(k)表示输出误差。通过公式推导得到以下结论。
(1)高斯函数的中心值cij和宽度值σij的更新调整
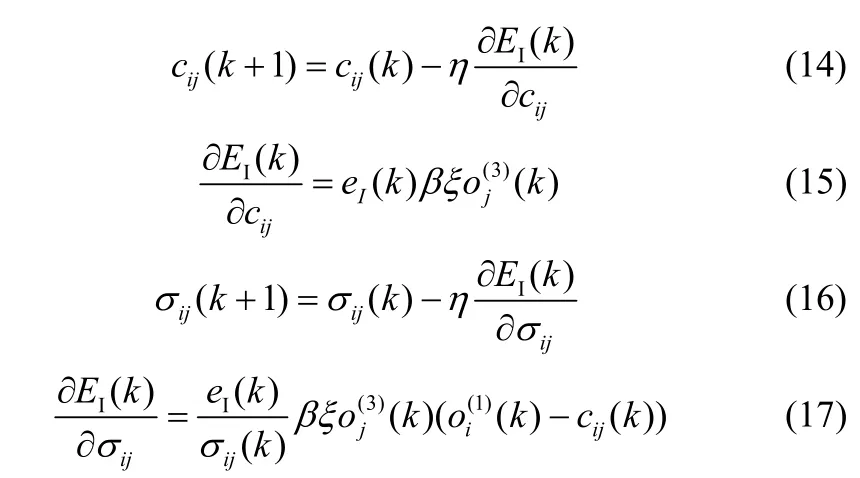
其中

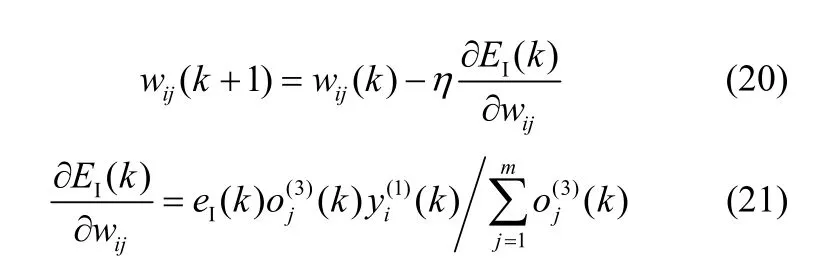
(3)网络学习率η的更新调整
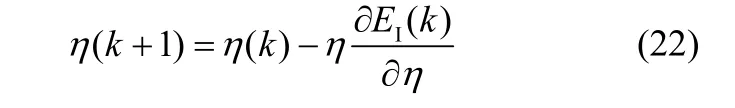
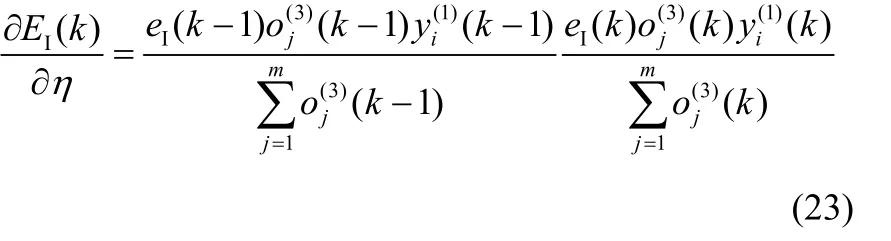
3 控制结果仿真及分析
3.1 控制系统设计
为了更好地验证SOTSFNN控制器的性能,将该控制器直接作用于控制对象,实现闭环反馈控制(图4)。

图4 SOTSFNN结构Fig.4 Diagram of control DO concentration
图中,给定值rin(k)为溶解氧浓度的期望值;控制器有两个输入量,分别为溶解氧浓度的实际值与期望值的误差量e(k)及误差的变化量;控制器的输出du(t)为氧传递系数的变化量;控制对象为溶解氧浓度。在整个控制过程中,每采样一次数据,确定模糊规则之后,对网络进行学习。采用梯度下降法对前件网络的隶属函数的中心值cij和宽度值σij、后件网络的权值wij以及学习率η进行学习。通过利用梯度下降学习算法来调整网络的学习率η,从而加快系统的寻优和收敛速度。
3.2 实验结果及分析
BSM1包含干燥、雨天和暴雨3种天气情况。文中选取雨天情况进行仿真。雨天包括前7天的晴好天气及8~11天时的连续降雨天气。针对系统的控制效果,通过ISE(平方误差积分)、IAE(绝对误差积分)和Max err(最大偏差)3个指标进行评判。
实验中数据的采样间隔为15 min。DO设定值为2 mg·L−1,输入量为DO的误差和误差的变化量,激活强度阈值设置为0.8。控制效果如图5所示。同时,文中对3种控制策略的结果进行比较,如表1所示。图6所示的是模糊规则数的增长情况。
从图6中可以发现,模糊规则的增长主要分为两个部分。第1部分是第1、2天,由于现有的模糊规则无法满足环境的要求,则需要进行模糊规则的增加及学习。在稳定之后则不在增加。第2部分是第8、9天,由于实验环境选择的是连续降雨天气,在第8~11天会有一个持续的降雨过程,由于环境的突变,此时现有的控制器结构无法满足环境的要求,需要增加模糊规则,从而更好的适应环境的变化。
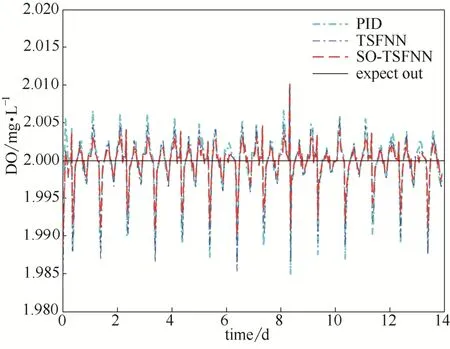
图5 雨天环境下控制效果对比Fig.5 Simulation of rainday
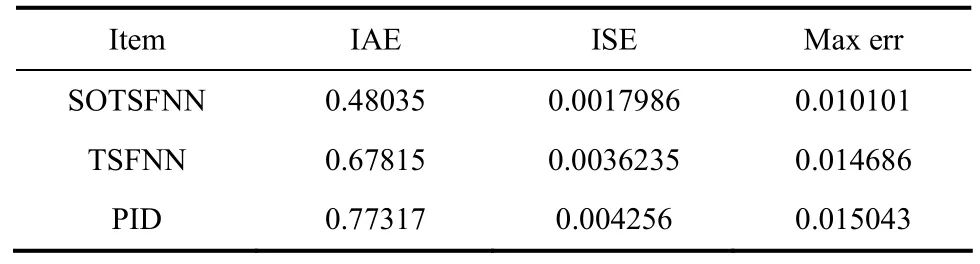
表1 控制效果数据对比Table 1 Comparison of control effect (same setpoint)

图6 模糊规则增长曲线Fig.6 Curve of fuzzy rules
从图5以及表1数据的对比可以发现,基于SOTSFNN系统的DO控制系统与PID及TSFNN控制相对比,具有更优的控制效果,稳定性及精度都相对较好。
为了更好地验证SOTSFNN控制器的稳定性和鲁棒性,文中对DO浓度的期望值做了如下改变:3~6 d设定值为1.8 mg·L−1,8~11 d设定值为2.2 mg·L−1,其余时间段均为2 mg·L−1。控制效果如图7所示。同时,与PID及TSFNN控制相比较,如表2所示。模糊规则增长曲线图如图8所示。
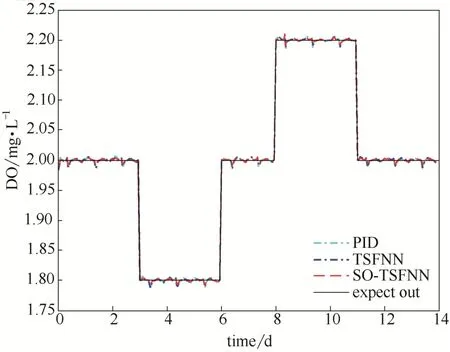
图7 变设定值控制效果对比Fig.7 Simulation based on different setpoint
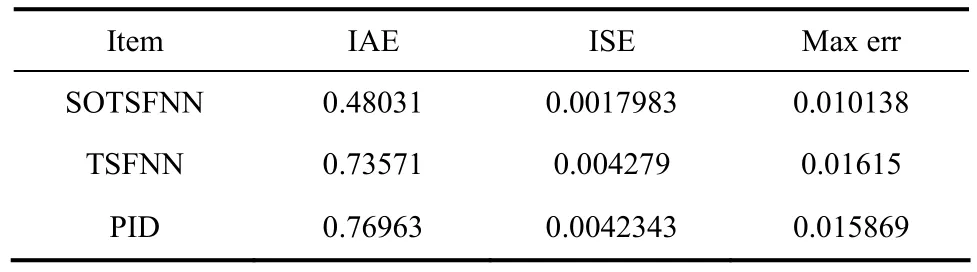
表2 变设定值控制效果数据对比Table 2 Comparison of control effect (vary-setpoint)
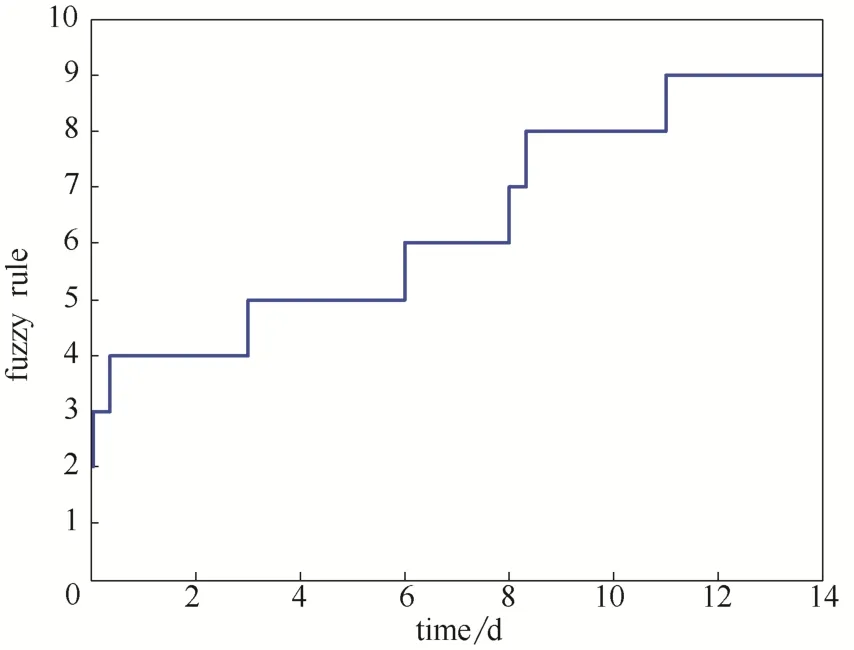
图8 变设定值模糊规则增长曲线Fig.8 Curve of fuzzy rules
从图7中可以看出,当期望值发生变化后,控制器能够很好地对DO进行跟踪控制,使DO维持在期望值附近。从图8中可以明显看出,当环境发生变化时,控制系统会根据当前环境的状况自组织的调整控制器结构,使控制器能够更好地稳定地对DO进行控制。
综合表2中的数据结果显示,基于SOTSFNN的控制器在污水处理过程中具有更优的控制性能以及较好的稳定性自适应性。
4 结 论
针对污水处理过程具有非线性、不确定性以及干扰严重等特点,在TS模糊神经网络的基础上,设计并实现了一种基于激活强度的自组织TS模糊神经网络。通过对模糊规则层激活强度的判断,来决定模糊规则的增长,进而自组织地调整网络结构,根据不同的环境实现较好的性能。
将SOTSFNN用作控制器,通过误差反向传播算法对各个参数和学习率进行调整,充分利用神经网络较好的学习能力和逼近能力。最重要的是在污水基准仿真平台上进行了应用,较好地实现了DO的跟踪控制。根据仿真结果能够表明本文提出的SOTSFNN控制器在面对环境的变化后,能够自适应地对控制结构进行调整,使控制器能够更好地满足当前环境的变化,实现较好的控制效果。合理设定污水处理过程仿真条件,通过与PID及TSFNN控制方法效果相比,文中提出的SOTSFNN具有更好的精度和控制性能;同时验证了文中SOTSFNN具有较好稳定性和适应性。
此外,从理论方面和实验方面能够说明,针对类似污水处理过程这种大规模、大时变的非线性系统,采用基于SOTSFNN的控制方法对其进行控制是可行的。
References
[1] 韩红桂, 甄博然, 乔俊飞. 动态结构优化神经网络及其在溶解氧控制中的应用 [J]. 信息与控制, 2010, 39(3): 354-360. DOI: 10.3969/j.issn.1002-0411.2010.03.016.
HAN H G, ZHEN B R, QIAO J F. Dynamic structure optimization neural network and its applications to dissolved oxygenic(DO) control [J]. Information and Control, 2010, 39(3): 354-360. DOI: 10.3969/j.issn.1002-0411.2010.03.016.
[2] PETRE E, SELISTEANU D, SENDRESCU D, et al. Nonlinear and neural networks based adaptive control for a wastewater treatment bioprocess [M]//Knowledge Based Intelligent Information and Engineering Systems. Berlin: Springer Berlin: Heidelberg, 2008: 273-280.
[3] GARRIDO J M, VAN BENTHUM W A J, VAN LOOSDRECHT, et al. Influence of dissolved oxygen concentration on nitrite accumulation in a biofilm airlift suspension reactor [J]. Biotechnology and Bioengineering, 1997, 53 (2): 168-178. DOI: 10.1002/(SICI)1097-0290(19970120) 53:2<168::AID-BIT6>3.0.CO;2-M.
[4] HOLENDA B, DOMOKOS E, REDEY A, et al. Dissolved oxygen control of the activated sludge wastewater treatment process using model predictive control [J]. Computers & Chemical Engineering, 2008, 32 (6): 1270-1278. DOI: 10.1016/j.compchemeng.2007.06.008.
[5] WAHAB N A, KATEBI R, BALFERUD J. Multivariable PID control design for activated sludge process with nitrification and denitrification [J]. Biochemical Engineering Journal, 2009, 45 (3): 239-248. DOI: 10.1016/j.bej.2009.04.016.
[6] VRECKO D, HVALA N, KOCIJAN J. Wastewater treatment benchmark: what can be achieved with simple control [J]. WaterScience & Technology, 2002, 45 (4/5): 127-134.
[7] LIU H B, YOO C K. Performance assessment of cascade controllers for nitrate control in a wastewater treatment process [J]. Korean Journal of Chemical Engineering, 2011, 28 (3): 667-673. DOI: 10.1007/s11814-010-0442-x.
[8] AYESA E, DE LA SOTA A, GRAU P, et al. Supervisory control strategies for the new WWTP of Galindo-Bilbao: the long run from the conceptual design to the full-scale experimental validation [J]. Water Science & Technology, 2006, 53 (4/5): 193-201. DOI: 10.2166/wst.2006.124.
[9] CARLSSON B, REHNSTROM A. Control of an activated sludge process with nitrogen removal—a benchmark study [J]. Water Science & Technology, 2002, 45 (4/5): 135-142.
[10] 潘海鹏, 徐玉颖. 基于BP网络的流浆箱双变量PID解耦控制 [J].化工学报, 2010, 61 (8): 2154-2158.
PAN H P, XU Y Y. Double variable PID decoupling control of headbox based on BP neural network [J]. CIESC Journal, 2010, 61 (8):2154-2158.
[11] KOTZAPETROS A D, PARASKEVAS P A, STASINAKIA A S. Design of a modern automatic control system for the activated sludge process in wastewater treatment [J]. Chinese Journal of Chemical Engineering, 2015, 23 (8): 1340-1349. DOI: 10.1016/j.cjche.2014. 09.053.
[12] 胡玉玲, 乔後飞. 变参数活性污泥系统溶解氧的模糊神经网络控制 [J]. 电工技术学报, 2004, 19 (3): 36-40.
HU Y L, QIAO J F. Fuzzy neural network control of DO in activated sludge system based on uncertain parameters [J]. Transactions of China Electrotechnical Society, 2004, 19 (3): 36-40.
[13] CHANDRAMOULI V, BRION G, NEELAKANTAN T R, et al. Backfilling missing microbial concentrations in a riverine database using artificial neural networks [J]. Water Research, 2007, 41 (1): 217-227. DOI: 10.1016/j.watres.2006.08.022.
[14] BELCHIOR C A C, ARAUJO R A M, LANDECK J A C. Dissolved oxygen control of the activated sludge wastewater treatment process using stable adaptive fuzzy control [J]. Computers & Chemical Engineering, 2012, 37 (4): 152-162. DOI: 10.1016/j.compchemeng. 2011.09.011.
[15] HAN H G, QIAO J F, CHEN Q L. Model predictive control of dissolved oxygen concentration based on a self-organizing RBF neural network [J]. Control Engineering Practice, 2012, 20 (4): 465-476. DOI: 10.1016/j.conengprac.2012.01.001.
[16] 张亚军, 柴天佑, 富月. 基于ANFIS与多模型的一类非线性系统的自适应控制方法 [J]. 化工学报, 2010, 61 (8): 2084-2091.
ZHANG Y J, CHAI T Y, FU Y. Adaptive control method for a class of nonlinear systems based on ANFIS and multiple models [J]. CIESC Journal, 2010, 61 (8): 2084-2091.
[17] ALEX J, BETEAU J F, COPP J B, et al. Benchmark for evaluating control strategies in wastewater treatment plants [C]//European Control Conference. Germany Karlsruhe, 1999: 99.
[18] JEPPSSON U, ROSEN C, ALEX J, et al. Towards a benchmark simulation model for plant-wide control strategy performance evaluation of WWTPs [J]. Water Science and Technology, 2006, 53 (1): 287-295. DOI: 10.2166/wst.2006.031.
[19] MURALISANKAR S, GOPALAKRISHNAN N, ALASUBRAMANIAM P. An LMI approach for global robust dissipativity analysis of T-S fuzzy neural network with interval time-varying delays [J]. Expert Systems with Applications, 2012, 39 (3): 3345-3355. DOI: 10.1016/j.eswa.2011.09.021.
[20] 王书斌, 单胜男, 罗雄麟. 基于T-S模糊模型与粒子群优化的非线性预测控制 [J]. 化工学报, 2012, 63 (S1): 176-187. DOI: 10.3969/j.issn.0435-1157.2012.z1031.
WANG S B, SHAN S N, LUO X L. Nonlinear predictive control based on T-S fuzzy model and particle-swarm optimization [J]. CIESC Journal, 2012, 63 (S1):176-187. DOI: 10.3969/j.issn.0435-1157.2012.z1031.
[21] CHEN C S. Robust self-organizing neural-fuzzy control with uncertainty observer for MIMO nonlinear systems [J]. IEEE Transactions on Fuzzy Systems, 2011, 19 (4): 694-706. DOI: 10.1109/TFUZZ.2011.2136349.
[22] QIAO J F, LI W, HAN H G. Soft computing of biochemical oxygen demand using an improved T-S fuzzy neural network [J]. Chinese Journal of Chemical Engineering, 2014, 22 (11/12): 1254-1259. DOI: 10.1016/j.cjche.2014.09.023.
研究论文
Received date: 2015-12-18.
Foundation item: supported by the National Natural Science Foundation of China (61533002, 61203099, 61225016).
Dissolved oxygen control method based on self-organizing T-S fuzzy neural network
QIAO Junfei, FU Wentao, HAN Honggui
(Beijing Key Laboratory of Computational Intelligence and Intelligent System, College of Electronic Information and Control Engineering, Beijing University of Technology, Beijing 100124, China)
Abstract:It is difficult to control the dissolved oxygen concentration of the wastewater treatment, a novel approach of control method based on the self-organizing T-S fuzzy neural network (SOTSFNN) is proposed. The essence of the approach according to the actual environment adjust the neuron self-adaptation in time, based on the activity intensity comparisons of the fuzzy rules layer, and construct the appropriate control structure, thus increase the accuracy of control effect. Meanwhile, the parameters of the controller are adjusted on line using error back propagation algorithm. Finally, the controller is applied to Benchmark Simulation Model No.1. The results indicate that the proposed SOTSFNN controller can achieve better control effect for dissolved oxygen concentration with good adaptability.
Key words:neural networks; control; dissolved oxygen concentration; dynamic simulation; self-organization algorithm
DOI:10.11949/j.issn.0438-1157.20151924
中图分类号:TP 183
文献标志码:A
文章编号:0438—1157(2016)03—0960—07
基金项目:国家自然科学基金项目(61533002,61203099,61225016);北京市科技新星计划项目(Z131104000413007);教育部博士点新教师基金项目(20121103120020);北京市教育委员会科研计划项目(KZ201410005002,km201410005001);北京市朝阳区协同创新项目(ZH14000177);高等学校博士学科点专项科研基金资助课题项目(20131103110016)。
Corresponding author:Prof. QIAO Junfei, fuwentao@emails.bjut.edu.cn
