一种基于自适应回归核函数的污水处理能耗模型
2016-05-11韩红桂张璐乔俊飞北京工业大学电子信息与控制工程学院北京100124
韩红桂,张璐,乔俊飞(北京工业大学电子信息与控制工程学院,北京 100124)
一种基于自适应回归核函数的污水处理能耗模型
韩红桂,张璐,乔俊飞
(北京工业大学电子信息与控制工程学院,北京 100124)
摘要:针对污水处理过程能耗模型难以建立的问题,提出了一种基于自适应回归核函数的建模方法。通过分析污水处理过程的运行特点,构建能耗与运行过程变量之间的关系,得到一种基于过程变量的能耗模型表达;同时利用梯度下降算法对能耗模型参数进行自适应调整,提高模型精度。最后,将设计的能耗模型应用于污水处理过程基准仿真平台BSM1和实际污水处理厂,实验结果表明该模型能够根据污水处理过程变量实时获得污水处理过程的能耗,具有较好的自适应特性和较高的精度。
关键词:能耗模型;污水处理过程;自适应回归核函数;过程变量
2015-12-28收到初稿,2016-01-11收到修改稿。
联系人及第一作者:韩红桂(1983—),男,博士研究生,教授。
引 言
城市污水处理过程的目标是实现出水水质达标的同时降低运行能耗[1]。然而,由于污水处理过程能耗影响因素众多,且各影响因素之间关系复杂,能耗模型难以建立,因此污水处理过程能耗模型的研究仍然是一个开放的问题[2-3]。
污水处理过程能耗主要包括泵送能耗和曝气能耗。Hernandez等[4]通过非放射数据包络分析方法计算污水处理过程能耗效率指标,并检测污水处理过程操作变量对能耗效率的影响。实验结果表明工厂规模、有机物含量的去除、生物反应器的类型等都会对能耗效率指标产生影响。Yi等[5]基于生物生态机理(bio-ecological combination method,BECM),提出了一种污水处理过程能耗模型表达,该模型表达总结了能耗与出水水质指标之间的关系。Kusiak 等[6]通过分析能耗与流速之间的关系,基于数据挖掘方法(data-mining method,DMM)建立了泵速和能耗与流量之间的模型表达式,实验结果显示该能耗模型精度超过90%。上述研究虽然建立了能耗的机理模型,但这些机理模型主要描述了污水处理过程能耗与单个过程变量之间的关系,而污水处理过程能耗影响因素众多,基于单变量的能耗模型不能准确表达污水处理过程的能耗[7-8]。为了获得更加客观的能耗和多个变量之间的关系,Yang等[9]在氧化沟工艺的基础上,提出了一种基于流体动力学(computational fluid dynamics,CFD)的能耗模型,描述了流速和溶解氧浓度与能耗和出水水质的关系。Vera等[10]通过将污水处理过程分成4个不同的装置:曝气装置,传统处理装置,延长曝气装置,序批式生物反应装置,比较不同装置中控制参数对能耗、出水水质和污泥产量的影响,获得了一种基于控制参数的能耗模型。Chen等[11]根据多目标优化的方法将出水水质和操作费用作为污水处理厂的目标,并根据3种不同天气情况的进水流量来研究开环和闭环条件下最优的污水处理运行性能指标。但是以上几种方法[9-11]均以污水处理工艺为基础分析能耗,由于该方法待整定参数过多,实际应用误差极大。
为了提高能耗模型精度,近年来,基于数据驱动的建模方法已广泛应用于污水处理中[12-13]。针对污水处理过程一些变量如化学需氧量等难以实时在线测量的问题,Qiao等[14]提出了一种基于改进的模糊神经网络(T-S fuzzy neural network,TSFNN)软测量方法,K均值聚类算法和梯度下降算法分别用于初始化和优化模糊神经网络,实验结果表明TSFNN能实时准确地测量BOD的值。利用核函数算法可将原始输入映射到高维特征空间来有效解决非线性化学和生物过程主要变量提取的特点,Woo 等[15]基于核函数偏最小二乘算法(kernel partial least squares,KPLS)提取污水处理过程预测与焦煤相关的主要变量。为了实时测量污水处理过程有机物的浓度,Huang等[16]提出了一种基于遗传算法的模糊神经系统(genetic algorithm-based neural fuzzy system,GA-NFS),利用自适应c均值聚类和遗传算法优化网络结构。实验结果显示GA-NFS能有效地实时测量COD、NO3−和PO43−等有机物浓度。Huang等[17]利用Elman神经网络模型建立了出水水质和能耗之间的关系,同时通过Elman神经网络的自组织特性来保证模型精度。以上研究通过数据驱动方法如神经网络、核函数等建立非线性模型并取得较好的效果,但没有充分考虑系统动力学特性。
为了获得能耗与过程变量之间的关系,本文提出了一种基于自适应回归核函数方法(adaptive regressive kernel function,ARKF)的污水处理能耗模型。首先,结合污水处理过程运行特点分析运行过程变量间的关系,设计一种基于过程变量的能耗模型表达;其次,为了提高能耗模型的精度,通过梯度下降算法对能耗模型参数进行调整,提高模型自适应能力;最后,将自适应回归核函数能耗模型应用于基准仿真平台BSM1(benchmark simulation platform,BSM1)和实际污水处理过程(wastewater treatment process,WWTP),取得了较好的结果。
1 污水处理过程分析
1.1 污水处理过程特点
污水处理过程中,除了提高污水处理系统的可靠性和稳定性,同时还能够降低运行与维护成本,保证出水水质,使其符合排放标准。目前许多城市采用活性污泥法污水生物处理技术,其污水处理运行过程为:原污水首先经过粗格栅间去除污水中呈悬浮状的较大体积固体污染物,然后通过进水泵进入初沉池,去除大部分的悬浮物和部分有机物,从而提高污水的净化效果。然后经过初沉池的出水进入曝气池,曝气池由缺氧区和好氧区组成,其作为活性污泥法的核心部分,决定污水处理的质量。缺氧区中污水通过“无氧呼吸”,进行反硝化脱氮反应,将内循环回流的硝态氮还原为氮气释放出来,有机物实现初步降解;好氧区发生硝化反应,氨氮转化为硝酸盐,有机物进一步被降解。随后污水流入二沉池进行固液分离,上层澄清液排入水体。
整个污水处理过程中存在着两种回流形式,第1种是从好氧区流至缺氧区的硝化液内回流,用来保证缺氧区获得大量的硝态氮进行反硝化;第2种则是从二沉池流至缺氧区的污泥回流,部分沉淀的污泥回流保证了曝气池所需的活性微生物和有机碳源。最后,二沉池中的剩余污泥(除回流污泥外)与初沉池中的污泥混合,进入污泥处理浓缩、硝化、脱水等过程。
1.2 污水处理工艺
在污水处理过程中,普遍采用活性污泥法,而A2/O生物脱氮除磷工艺是传统活性污泥工艺、生物硝化和反硝化工艺、以及生物除磷工艺的综合,A2/O工艺流程及其各部分功能如图1所示。
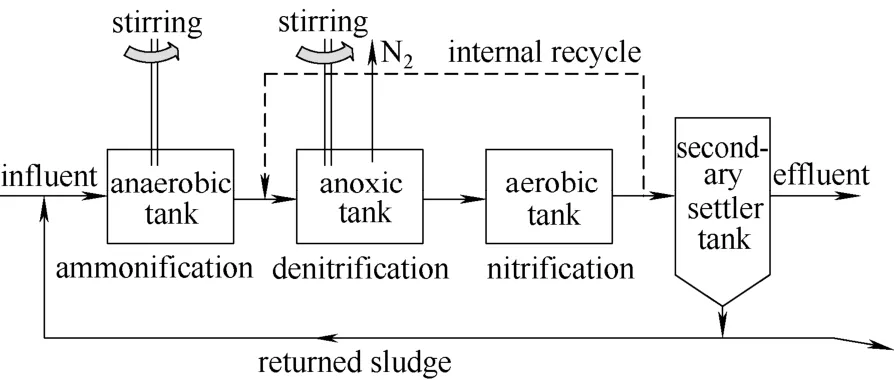
Fig.1 A2/O工艺流程及各部分功能Fig.1 A2/O technological process and functional diagram of each part
A2/O工艺由于具有同时脱氮和除磷的功能,相对于其他同步脱氮除磷工艺具有构造简单、总水力停留时间短、运行费用低、控制复杂性小、不易产生污泥膨胀等特点[18]。
2 能耗相关变量分析
2.1 能耗分析
通过污水处理过程基准仿真平台BSM1得到的能耗表达为[19]
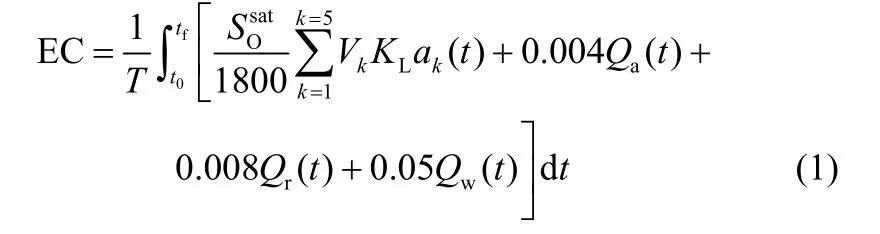
式中,EC为能耗;Vi为反应池的体积,V1= V2= 1000 m3,V3= V4= V5= 1333 m3;KLa为氧传递系数,反应池1和2的KLa为0 h−1,反应池3 和4的KLa为10 h−1,反应池5的KLa实时变化以控制溶解氧(SO)浓度保持在2 mg·L−1;为溶解氧设定值,通常取为8 mg·L−1;T为反应周期;Qa为内回流,用于控制硝态氮(SNO)浓度保持在1 mg·L−1;Qr为外回流,用于控制混合悬浮液固体(MLSS)浓度;Qw为污泥排放量,在BSM1中污泥排放量为常数[20]。从式(1)可得EC与SO、SNO、MLSS等变量相关。
2.2 变量与能耗的关系
溶解氧是影响污水处理过程有机物降解速率、出水水质、运行费用以及污泥沉淀性能的主要影响因素。当溶解氧浓度过高时,微生物絮凝遭到破坏而使得悬浮固体沉降性能变差,能耗过高;当溶解氧浓度过低时,导致出水水质变差,延长处理时间。
硝态氮浓度能够描述反硝化反应的进程,当缺氧区硝态氮浓度较小或为零时,就会进入厌氧状态,造成缺氧区的反硝化潜力无法被充分利用;如果硝态氮浓度过高,反而破坏了反硝化环境,无法提高氮的去除。同时,氨氮含量过高,导致-N的氧化,易造成水体中溶解氧浓度降低,引起出水水质变差;另一方面,含量过高抑制硝化菌活性,影响硝化反应的进行。
混合悬浮液固体用来表达微生物浓度,与自养菌浓度、异养菌浓度等变量相关,可通过污泥回流量控制污泥回流的程度,保证生化池中适当浓度的微生物。当混合悬浮液浓度过高,就会造成出水水质变差;若混合悬浮液浓度过低,细菌的生长率下降且污泥回流量过少,不仅影响处理效果,而且能耗增加。
3 基于自适应回归核函数的污水处理能耗模型
实际污水处理过程中由于复杂的非线性过程,多变量影响,且相互耦合等特点使得BSM1基准仿真平台得到的常系数能耗模型不适用于实际污水处理过程能耗计算,通过污水处理过程动力学方程分析与能耗相关的过程变量,利用自适应回归核函数方法建立能耗模型。

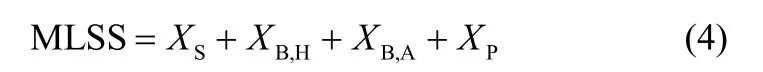
通过式(3)~式(4)可得SO、SNO变化量与SS、XB,A、XB,H、SNH之间存在直接关系,MLSS计算公式与XB,A、XB,H直接相关,且SO、SNO、MLSS直接影响EC,因此选择与能耗相关的过程变量为SO、SNO、XB,A、XB,H、SNH、SS。
为探究EC与SO、SNO、SS、XB,A、XB,H、SNH之间的关系,选择EC作为输出变量,SO、SNO、SS、XB,A、XB,H、SNH作为输入变量,因此可将输入变量与输出变量之间的关系描述为
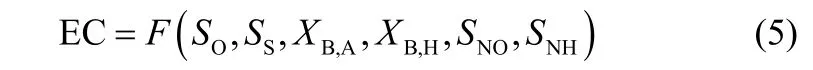
式中,F(·)为EC与输入变量间的函数关系。
为更好地表达EC与SO、SNO、SS、XB,A、XB,H、SNH之间的关系,自适应回归核函数模型用于建立输入变量与输出变量之间的关系。自适应回归核函数模型表达为
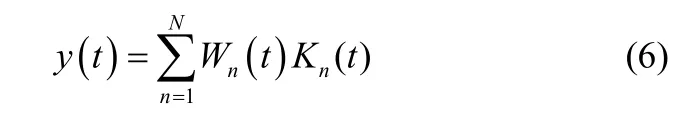
式中,y( t )为t时刻模型输出;Wn(t)为t时刻第n个核函数连接权值;N为核函数个数;Kn(t)为t时刻第n个核函数,选择具有强非线性表达能力的径向基核函数
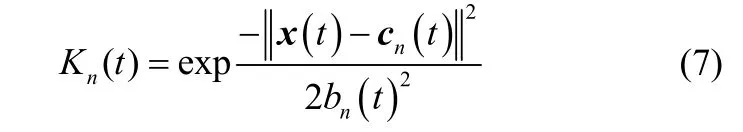
式中,x(t)为t时刻核函数输入,也是自适应回归核函数模型输入;cn(t)为t时刻第n个核函数中心;bn(t)为t时刻第n个核函数宽度。
为提高模型精度,梯度下降算法用于自适应调整模型参数。定义误差平方和
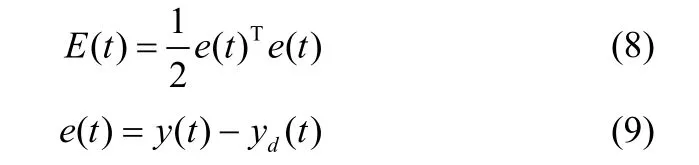
式中,E(t)为t时刻误差平方和;e(t)为t时刻实际输出与期望输出间的误差;yd(t)为t时刻期望输出。权值,中心和宽度调整公式为

式中,W(t+ 1)、c(t+ 1)、b(t+ 1)分别为t+1时刻所有核函数连接权值、中心、宽度,ΔW(t)、Δc(t)、Δb(t)为t时刻所有核函数连接权值、中心、宽度调整量,所有核函数连接权值、中心、宽度调整公式为
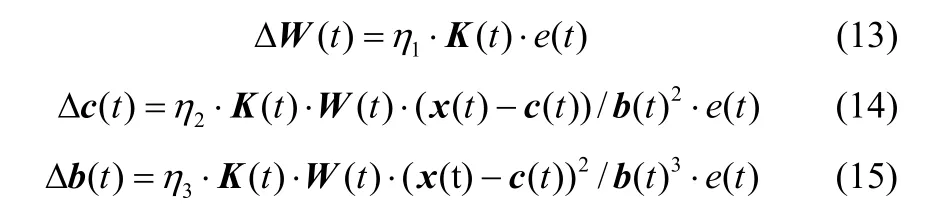
式中,K(t)为所有核函数;η1、η2和η3为学习率。
4 实验与结果分析
4.1 实验设计
为提高模型精度,得到更为准确的能耗值,通过两种情况对能耗模型进行验证。第1种情况选择基准仿真平台BSM1的330组数据,在该组数据中包含同一时间能耗与其过程变量的数据,随机选取280组数据作为训练样本,随机选取50组数据作为测试样本。第2种情况选择2014年高碑店污水处理厂的180组数据,在该组数据中包含同一时间能耗与其过程变量的实测数据,随机选取130组数据作为训练样本,随机选取50组数据作为测试样本。具体的步骤如下。
(1)首先利用训练样本,通过式(6)和式(7)计算模型训练输出,得到能耗模型训练输出与实际输出的比较图以及能耗模型训练输出与实际输出之间的误差图。
(2)基于训练得到的能耗模型,利用测试样本计算能耗模型测试输出,得到能耗模型测试输出与实际输出的比较图以及能耗模型测试输出与实际输出之间的误差图。
(3)依据式(16)计算模型误差率,分析模型精度,检验模型的预测性能。
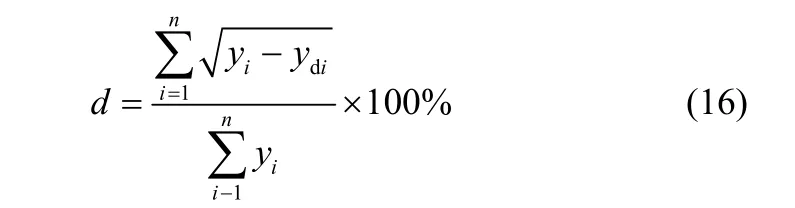
式中,n表示样本总数;i表示样本序号;d表示误差率;yi表示第i个样本对应的能耗实际输出;ydi表示第i个样本对应的能耗期望输出。
4.2 实验结果与分析
图2~图5给出BSM1中能耗的训练效果图和训练误差,测试效果图及测试误差,图6~图9给出实际污水处理过程能耗的训练效果图和训练误差,测试效果图及测试误差,表1给出BSM1中不同能耗模型的精度对比,表2给出实际污水处理过程不同能耗模型的精度对比。

Fig.2 BSM1能耗训练结果Fig.2 Training results of EC in BSM1
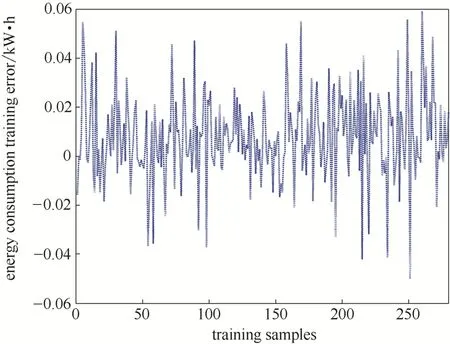
Fig.3 BSM1能耗训练误差Fig.3 Training errors of EC in BSM1

Fig.4 BSM1能耗测试结果Fig.4 Testing results of EC in BSM1
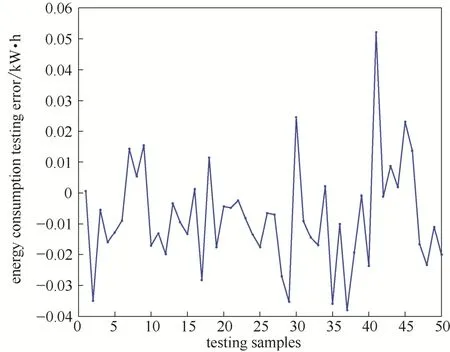
Fig.5 BSM1能耗测试误差Fig.5 Testing errors of EC in BSM1

Fig.6 实际水厂能耗训练结果Fig.6 Training results of EC in WWTP
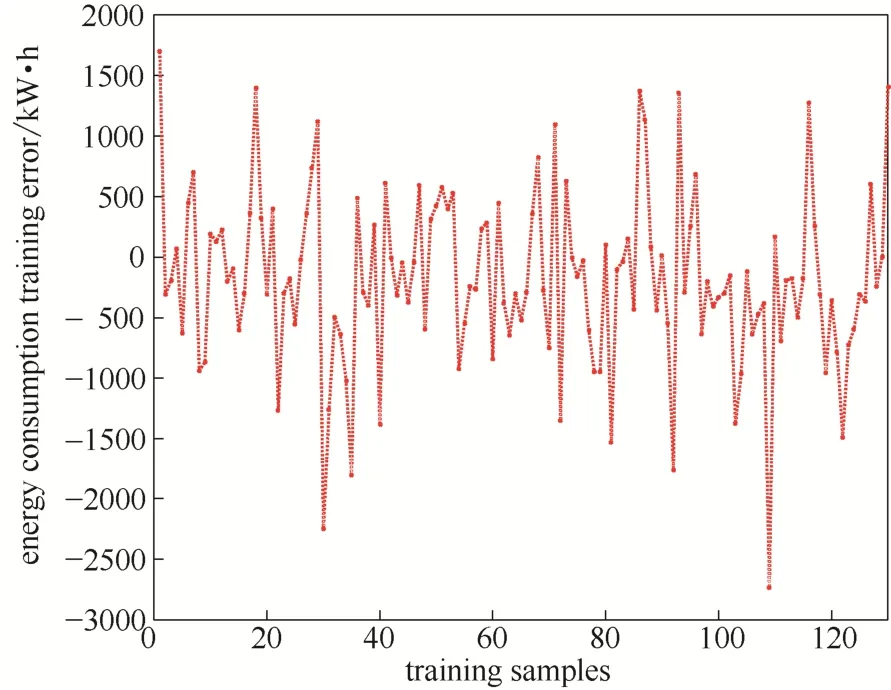
Fig.7 实际水厂能耗训练误差Fig.7 Training errors of EC in WWTP
从图2可以看出BSM1中能耗模型训练输出能准确跟踪实际输出的变化趋势,使得训练输出准确地逼近实际输出,训练输出与实际输出误差较小,模型的训练误差如图3所示,保持在±0.05 kW·h范围内。图4给出了能耗模型测试输出与实际输出的对比,结果表明测试输出与实际输出误差较小,误差范围为±0.05 kW·h,能耗模型测试误差结果如图5所示。

Fig.8 实际水厂能耗测试结果Fig.8 Testing results of EC in WWTP
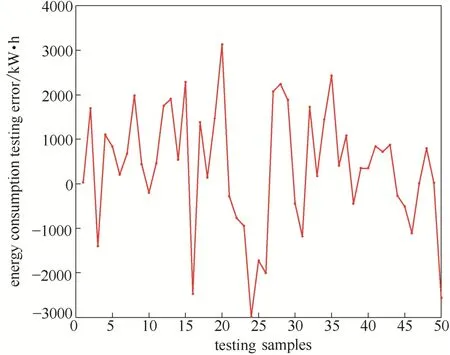
Fig.9 实际水厂能耗测试误差Fig.9 Testing errors of EC in WWTP

表1 BSM1模型精度对比Table 1 Comparison among different models in BSM1

表2 WWTP模型精度对比Table 2 Comparison among different models in WWTP
表1给出不同能耗模型精度对比,分别将BSM1中自适应回归核函数能耗模型(ARKF)与基准仿真平台-膜生物反应器能耗计算方法(benchmark simulation platform membrane biological reactor,BSM-MBR)、总成本指数模型方法(total cost index model,TCIM)做比较,结果表明数据驱动能耗模型精度可达97.9%,比其他基准仿真平台能耗建模方法具有更高的精度。
图6给出实际污水处理过程中能耗模型训练输出与实际输出的比较,结果显示能耗模型训练输出不仅变化趋势与实际输出一致,且输出值与实际能耗输出值较为接近,训练输出与实际输出误差较小,保持在±2500 kW·h范围内,模型的训练误差如图7所示。图8给出能耗模型测试输出与实际输出的对比,结果表明测试输出能较好地逼近实际输出,模型测试输出与实际输出误差范围为±3000 kW·h,能耗模型测试误差结果如图9所示。
表2给出不同能耗模型精度对比,分别将实际污水处理过程中自适应回归核函数模型(ARKF)与计算流体动力学模型(CFD)、数据挖掘方法(DMM)和生物-生态结合方法(BECM)做比较,结果表明数据驱动能耗模型精度可达96.38%,精度高于其他能耗建模方法。
实验结果表明自适应回归核函数能耗模型不仅可应用于基准仿真平台BSM1中,还可应用于实际的污水处理过程中。本文提出的自适应回归核函数模型通过分析污水处理过程特点选取过程变量,能很好地反映污水处理过程动力学特性,同时该模型参数可根据梯度下降算法进行自适应调整,提高模型的精度。实验结果表明自适应回归核函数能耗模型具有较好的自适应特性与较高的精度,因此基于自适应回归核函数模型方法可应用到实际的建模过程中。
5 结 论
针对能耗模型影响变量众多,且模型难以建立的问题,通过污水处理过程运行特点分析能耗与过程变量间的关系,本文提出了一种基于自适应回归核函数的能耗模型,通过梯度下降算法对模型参数进行自适应调整,使模型具有更高的精度,同时将自适应回归核函数能耗模型应用于基准仿真平台BSM1与实际的污水处理过程中,并与其他能耗建模方法进行比较,根据理论分析与实验结果得到如下结论。
(1)通过机理分析,获得污水处理过程中与能耗相关的过程变量,过程变量共有6个,分别是SO、SS、XB,A、XB,H、SNO和SNH,将6个过程变量作为输入变量,能耗作为输出变量,建立输入变量与输出变量之间的关系。
(2)基于自适应回归核函数的能耗模型能直接反映与过程变量之间的关系,同时模型参数可利用自适应梯度下降算法进行调整,不仅使模型具有更高的自适应特性,而且提高了模型精度。在BSM1中自适应回归核函数能耗模型精度可达97.9%,在实际污水处理过程中自适应回归核函数能耗模型精度96.38%,高于其对比的能耗模型精度。
(3)基于自适应回归核函数的能耗模型研究不仅可成功应用到基准仿真平台BSM1中,而且可应用于实际污水处理过程中,因此其结果可推广到实际研究应用中,具有实际工程价值。
References
[1] HAN H G, QIAN H H, QIAO J F. Nonlinear multiobjective model-predictive control scheme for wastewater treatment process [J]. Journal of Process Control, 2014, 24 (3): 47-59.
[2] PALMA C, CARVAJAL A, VASQUEZ C, et al. Wastewater treatment for removal of recalcitrant compounds: a hybrid process for decolorization and biodegradation of dyes [J]. Chinese Journal of Chemical Engineering, 2011, 19 (4): 621-625.
[3] SHAWAQFEH A T. Removal of pesticides from water using anaerobic-aerobic biological treatment [J]. Chinese Journal of Chemical Engineering, 2010, 18 (4): 672-680.
[4] HERNANDEZ S F, MOLINOS S M, SALA G R. Energy efficiency in Spanish wastewater treatment plants: a non-radial DEA approach [J]. Science of the Total Environment, 2011, 409 (14): 2693-2699.
[5] YI X N, FAN Y H, HU C F, et al. Study on bio-ecological combination process with high efficiency and low energy consumption for municipal wastewater treatment [J]. Bioinformatics and Biomedical Engineering, 2009, 3 (1): 11-13.
[6] KUSIAK A, ZHANG Z J, ZENG Y H. Modeling and analysis of pumps in a wastewater treatment plant: a data-mining approach [J]. Engineering Applications of Artificial Intelligence, 2013, 26 (7): 1643-1651.
[7] WANG Q, NAN S, DOU M. Experimental investigation on nanofiltration treatment of waste water containing low concentration ammonium perfluorooctanoate [J]. Journal of Chemical Engineering of Chinese Universities, 2008, DOI: 10.3321/j.issn.1003-9015.2008.04.025.
[8] FEINI L, ZHANG G, QIN M, et al. Performance of nanofiltration and reverse osmosis membranes in metal effluent treatment [J]. Chinese Journal of Chemical Engineering, 2008, 16 (3): 441-445.
[9] YANG Y, YANG J, ZUO J, et al. Study on two operating conditions of a full-scale oxidation ditch for optimization of energy consumption and effluent quality by using CFD model [J]. Water Research, 2011, 45 (11): 3439-3452.
[10] VERA I, SAEZ K, VIDAL G. Performance of 14 full-scale sewage treatment plants: comparison between four aerobic technologies regarding effluent quality, sludge production and energy consumption [J]. Environmental Technology, 2013, 34 (15): 2267-2275.
[11] CHEN W L, LU X W, YAO C H. Optimal strategies evaluated by multi-objective optimization method for improving the performance of a novel cycle operating activated sludge process [J]. Chemical Engineering Journal, 2015, 260 (1): 492-502.
[12] WAHAB N A, KATEBI R, BALDERUD J, et al. Data-driven adaptive model-based predictive control with application in wastewater system [J]. IET Control Theory and Applications, 2011, 5 (6): 803-813.
[13] WANG X R, HUANG B, CHEN T W. Data-driven predictive control for solid oxide fuel cells [J]. Journal of Process Control, 2007, 17 (2): 103-114.
[14] QIAO J F, LI W, HAN H H. Soft computing of biochemical oxygen demand using an improved T-S fuzzy neural network [J]. Chinese Journal of Chemical Engineering, 2014, 22 (11): 1254-1259.
[15] WOO S H, JEON C O, YUN Y S, et al. On-line estimation of key process variables based on kernel partial least squares in an industrial cokes wastewater treatment plant [J]. Journal of Hazardous Materials, 2009, 161 (1): 538-544.
[16] HUANG M Z, MA Y W, WAN J Q, et al. A sensor-software based on a genetic algorithm-based neural fuzzy system for modeling and simulating a wastewater treatment process [J]. Applied Soft Computing, 2015, 27: 1-10.
[17] HUANG X Q, HAN H G, QIAO J F. Energy consumption model for wastewater treatment process control [J]. Water Science & Technology, 2013, 67 (3): 667-674.
[18] MOON T, KIM M S, KIM S J, et al. Evaluation of rule-based control strategies according to process state diagnosis in A2/O process [J]. Chemical Engineering Journal, 2013, 222 (1): 391-400.
[19] VEGA P, BALLESTEROS F. Integration of setpoint optimization technologies into nonlinear MPC for improving the operation of WWTPs [J]. Computers and Chemical Engineering, 2014, 68 (10): 78-95.
[20] JEPPSSON U, PONS M N. The COST benchmark simulation model—current state and future perspective [J]. Control Engineering Practice, 2004, 12 (3): 299-304.
[21] MAERE T, VERRECHT B, MOERENHOUT S, et al. BSM-MBR: a benchmark simulation model to compare control and operational strategies for membrane bioreactors [J]. Water Research, 2011, 45 (6): 2181-2190.
[22] VANROLLEGHEM P A, GILLOT S. Robustness and economic measures as control benchmark performance criteria [J]. Water Science & Technology, 2002, 45 (4/5): 117-126.
研究论文
Received date: 2015-12-28.
Foundation item: supported by the National Natural Science Foundation of China (61533002, 61203099, 61225016), the Beijing Nova Program (Z131104000413007), the Program Foundation from Ministry of Education (20121103120020), Beijing Municipal Education Commission Science and Technology Development Program (KZ201410005002, km201410005001), the Collaborative Innovation Program (ZH14000177), the Specialized Research Fund for the Doctoral Program of China (20131103110016) and the First Class Program Foundation from China Postdoctoral Science Foundation (2014M550017).
An energy consumption model of wastewater treatment process based on adaptive regressive kernel function
HAN Honggui, ZHANG Lu, QIAO Junfei
(College of Electronic Information and Control Engineering, Beijing University of Technology, Beijing 100124, China)
Abstract:Due to the difficulty in establishing the energy consumption model for the wastewater treatment process, an adaptive regressive kernel function is developed in this paper. Based on the characteristic analysis of the wastewater treatment process, the relationship between the energy consumption and the process variables is obtained. And an energy consumption model is established with the process variables. Meanwhile, the model parameters are adjusted adaptively by using the gradient descent algorithm to improve its accuracy. Finally, this proposed energy consumption model is applied to benchmark simulation platform and a real wastewater treatment process. The results show that this energy consumption model is able to display the operate cost of wastewater treatment process online according to the process variables, with good adaptivity and accuracy.
Key words:energy consumption model; wastewater treatment process; adaptive regressive kernel function; process variables
DOI:10.11949/j.issn.0438-1157.20151977
中图分类号:TQ 028.8
文献标志码:A
文章编号:0438—1157(2016)03—0947—07
基金项目:国家自然科学基金项目(61533002,61225099,61225016);北京市科技新星计划项目(Z131104000413007);教育部博士点新教师基金项目(20121103120020);北京市教育委员会科研计划项目(KZ201410005002,km201410005001);北京市朝阳区协同创新项目(ZH14000177);高等学校博士学科点专项科研基金(20131103110016);中国博士后科学基金一等资助项目(2014M550017)。
Corresponding author:Prof. HAN Honggui, rechardhan@sina.com
