动态RBF神经网络在浮选过程模型失配中的应用
2016-05-11王晓丽黄蕾杨鹏阳春华中南大学信息科学与工程学院湖南长沙410083
王晓丽,黄蕾,杨鹏,阳春华(中南大学信息科学与工程学院,湖南 长沙 410083)
动态RBF神经网络在浮选过程模型失配中的应用
王晓丽,黄蕾,杨鹏,阳春华
(中南大学信息科学与工程学院,湖南 长沙 410083)
摘要:铝土矿泡沫浮选过程中,因矿浆的快速沉淀等原因工艺参数在线检测困难,且入矿性质变化频繁,造成浮选过程参数随入矿的变化而不断改变。而通常建立的静态软测量模型利用固定样本集训练得到,当矿源变化时容易发生模型失配现象,使模型不能跟踪当前对象。针对变矿源下的模型失配问题,本文提出基于隐层节点动态分配和模型参数动态修正策略的RBF神经网络建模方法,用于铝土矿浮选过程酸碱度的在线检测建模。实际生产数据仿真结果表明该方法能够有效解决模型失配的问题。
关键词:泡沫浮选过程; 动态RBF神经网络;模型失配;工况迁移
2015-12-21收到初稿,2016-01-05收到修改稿。
联系人及第一作者:王晓丽(1981—),女,副教授。
引 言
铝土矿泡沫浮选过程中,因矿浆具有快速沉淀特性,矿浆浓度、粒度和pH等过程参数无法在线检测,使得软测量技术对浮选过程具有重要作用。由于铝土矿浮选过程矿石来源复杂,造成矿石性质多变,对浮选过程工艺参数产生重要影响。为保持生产的稳定性,实际生产采用配矿的方式,尽量保证在一段时间内入矿性质是一致的,此种情况下采用静态的神经网络模型能够取得很好的软测量效果。但由于矿源的复杂性,难以保证长时间的恒矿源供矿,使得矿石性质变化频繁,过程参数也不断变化。因而随着时间的推移,最初建立的静态神经网络模型已不能反映当前对象,产生“模型失配”现象。基于数据的建模方法对实际生产过程中的动态问题建模时均存在这样的问题,因此对动态过程的软测量建模问题仍是研究的难点和热点[1]。
处理模型失配问题通常有两种策略[2-3]:一是采用最近样本对模型进行重训练修正,如文献[3]采用对象重辨识的方法处理对象变化时出现的模型与对象失配问题;二是在原有模型的基础上对模型的结构和参数加以调整[4-7]。由于重训练建模的时间空间代价高,难以适用于实时系统,所以工业应用普遍采取第二种策略。
动态神经网络具有适应变化的能力,包括含反馈环节的神经网络[8-9]、具有时变参数的神经网络[10]、节点资源动态调整的神经网络[11-12]。最初引入动态网络思想的是Platt[13],他研究了隐层节点资源的动态分配来实现模型的动态调整修正,将该模型用于混沌时间序列中,并获得了相当好的效果。此后,引起了业界的广泛关注。但是因为Platt提出的RAN方法采用LMS(least mean squart)算法来对网络参数进行修正,对大样本对象会出现收敛速度慢的问题。Kadirkamanathan等[14]采用扩展的卡尔曼滤波器(extend Kalman filter)算法来代替LMS算法,加快了RAN网络的收敛速度,并可以降低网络结构的复杂程度,由于使用了扩展卡尔曼滤波器算法,故称为RAN-EKF。但是RAN神经网络只能一贯地添加隐层节点,对于在线模型,易导致模型臃肿、计算耗时等。Song等[7]针对RAN网络中创建隐层节点的新颖性条件太疏松,通过均方根滑动窗口方法(RMS)抑制突发噪声的影响,达到控制网络规模的效果。Lu等[15]提出了一种最小资源分配网络模型(MRAN)用于解决隐层节点过多的问题,从而使动态网络能够很好地控制自己的网络规模。
鉴于矿浆酸碱度对浮选生产的重要性,本文以浮选矿浆的酸碱度为具体对象,提出了基于动态RBF神经网络的建模方法以解决酸碱度软测量模型失配问题。针对矿源变化造成的过程参数变化问题,利用动态网络自身特性来动态地增删隐节点并修正网络参数,从而实现模型对对象的实时跟踪。
1 面向模型失配的动态神经网络建模方法研究
浮选实际生产过程中酸碱度的控制存在如下特点:矿石变化会引起酸碱度控制范围的整体迁移。静态的神经网络模型已被用于浮选生产,但在生产换矿时,静态模型给出的相关软测量参数往往有很大的偏差,这是因为静态神经网络模型没有考虑对新增样本不适时的模型结构调整问题,即在整个学习训练过程中,模型的结构及参数都是固定的。而矿石变化导致模型与当前对象失配,使参数检测、预测、故障诊断等都会发生异常。
神经网络适用于内插问题,而对外推问题的适应能力差,即神经网络只对学习范围内(不仅仅指离散训练集,还包括离散集囊括的范围)的数据有较准确的感知能力,而对学习范围外的数据基本上没有识别能力,因此需要一些方法使其适应学习范围外的样本。
1.1 样本失配类别
模型失配是指模型因各种原因随着时间的迁移无法与对象特性匹配的问题。在此,为了清晰地描述浮选过程的特点,设矿源有A和B两个不同的时段,RBF网络模型构建于A时段用于浮选过程酸碱度的在线检测,则存在如下两种模型失配情况。1.1.1 内插域中的不一致样本 在此,不一致样本是指在正常的生产条件下,具有相同或相似泡沫表面特征向量(模型的输入)但酸碱度存在显著差异的样本。不一致样本的出现并非偶然因素或系统的异常导致,而是一种因外界条件改变导致工况(如酸碱度)整体性迁移的情况。生产过程可能仍处于正常状态,但是通过监控系统获取的工艺参数以及根据这些参数做出的工况判断可能都是不正常的,此时的数学描述如下。
A时段和B时段的一对样本SA(xi,yi)、SB(xj,yj),其中x为泡沫表面特征向量(即酸碱度值软测量模型的输入向量),y为酸碱度值。采用欧几里德距离表示其相似性,存在如下关系
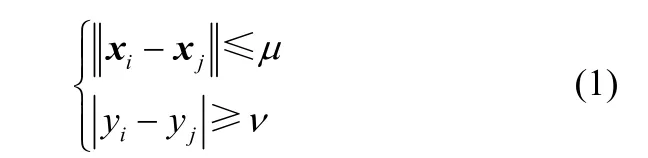
式中,μ、ν为大于0的参数,且μ为较小的正数,ν为较大的正数。
即如存在参数μ、ν使式(1)成立,表明样本SA和SB的特征向量相同或相似,酸碱度值却有明显差异。而神经网络建模方法存在一条原则:相似的条件下相似输入通常应生成网络中相似的表示。而上面输入相似的样本其输出不同,体现了矿源变化时存在不相似的条件。
1.1.2 外推域中的样本 由于神经网络具有的能力是通过学习得来的,对外推域内的样本没有识别能力。如图1,对于内插域内的和外推域内的,存在(π为较大的正数),此时同样会产生模型失配的问题。
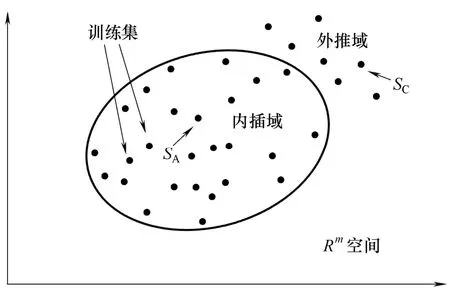
图1 内插域空间与外推域空间Fig.1 Interpolation and extrapolation domain space
1.2 基函数神经网络
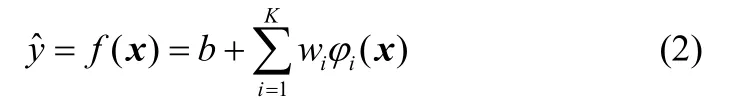
式中,φi()是m维空间的一个函数,采用高斯函数为
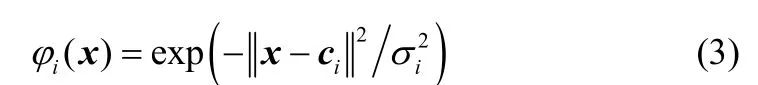
式中,ci是径向基函数的中心;K为中心的个数。
为了便于分析,图2给出了参数c、σ不同时高斯函数ϕ(x )= exp[− (x− c )2/σ2]的变化曲线。
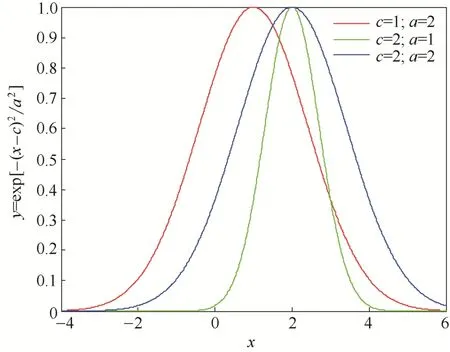
图2 高斯基函数随参数变化Fig.2 Gauss function with different parameters
由图2可知,参数c主要是影响φ(x)的左右位置,参数σ则主要是影响φ(x)的胖瘦程度即密集程度,σ越小点的分布越集中。同时可知,当x与c相等时,φ(x)取最大值;当x与c不等时,随着x 与c之间的距离变大,φ(x)几乎趋近于0。由此容易得出,对φ(x)而言,当x与c越相似时,φ(x)越大,能对以c为中心的局部空间做出更好的响应,而对离c远的输入空间的响应几乎可以忽略,从而做到输入空间的域划分。因此,如变矿源时出现外推域样本且网络无法正常响应时,则可以通过新增中心趋近样本的隐层节点来解决,这为后文中动态网络节点的分配提供了理论依据。
1.3 神经网络节点动态分配算法
RBF神经网络的建模过程在此不再赘述,本小节主要描述网络结构失配时的节点动态调节策略。图3为含隐节点动态分配的RBF网络。
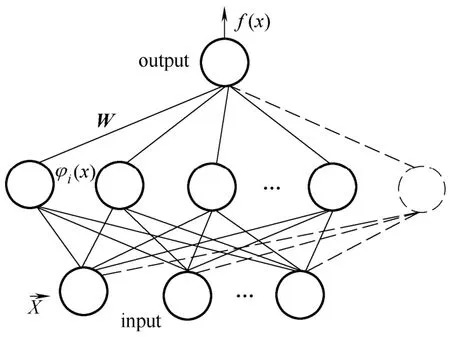
图3 隐节点动态分配的RBF网络Fig.3 RBF network with dynamic allocation of hidden nodes
当出现新增样本时,判断是否该为其增加一个隐层节点。RAN通过判断新颖性条件是否满足来动态调整隐含层节点的数目,采用经典的新颖性判定规则[13-14,16],即只有当满足如下关系时需要分配新节点
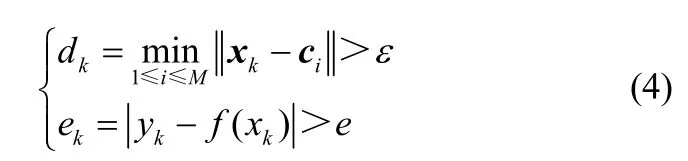
式中,M为当前隐含层的节点数;ci为隐含层的中心;dk为与xk最接近的ci之间的欧几里得距离;ek为样本对应的模型误差,xk经过归一化处理,这里ε取0.27,e取0.1。
为了防止个别异常数据构成的病态样本,再添加误差频率规则:在滑动窗口区间内,ηabnormal等于样本中满足的数量除以样本总数。
如果样本满足上述新颖性和误差频率条件,则为样本建立一个新隐含层,新增节点参数如下:。
详细算法[17-18]描述如下:
(1)获取模型参数,给阈值参数赋值,并考虑新增样本(xk,yk);
(3)如果ek大于e且ηabnormal大于阈值ηshre同时成立,则进入步骤(4);否则跳出此次检查;
(4)若dk不满足新颖性规则,则不增加节点,进入步骤⑥来调整网络结构参数;否则进入步骤(5);
1.4 相似节点的合并和持续低贡献节点的剔除1.4.1 相似节点的合并 由图2高斯函数可知,高斯基函数主要受基函数中c和σ影响。其中c与样本输入密切相关,能够表达出隐节点对样本的激活能力的强弱。因此,可以利用这点性质考察隐层节点的高斯基函数计算任意两基函数之间的空间夹角,判断节点的相似度。为简化计算,可以近似计算ci与cj之间的夹角来判断节点的相似度。如果ci、cj之间的夹角θij<θmin(θmin是设定的夹角阈值),则表明二者较相似,然后两相似隐层节点按如下方式合并合并完成后,即将节点i、节点j用一个节点k
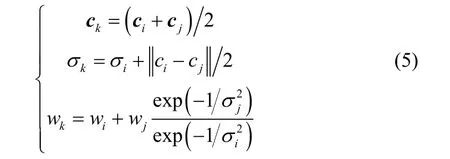
替代。再采用式(5)的最后一个式子调整网络的权值参数,以使网络尽量与原网络相似,能较精准地跟踪对象。
1.4.2 持续低贡献节点的剔除 对于网络中隐层节点的高斯基函数,如果在很大频度(连续L个样本)上都处于未激活状态,则可以考虑将其删除。删除后,仍需调整网络的权值参数使模型与对象匹配。
考虑某一隐节点ci,对于连续L个样本(xj,yj),如果都存在成立,则表明该隐节点为持续低贡献节点,可剔除。
删除低贡献节点后,用下述方法更新网络权值参数。定义误差目标函数为用误差目标函数来调整神经网络的参数
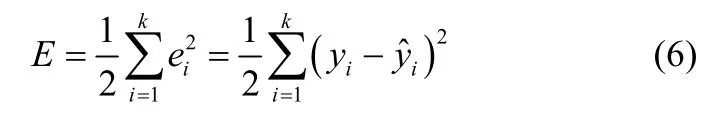

式中,m为剔除低贡献节点后的神经元个数。
2 生产数据仿真与分析
以泡沫浮选过程中泡沫表面特征为输入,以矿浆酸碱度为输出,采用本文所提出的动态神经网络对矿浆酸碱度进行在线估计建模。为对比分析动态神经网络模型的性能,同时对静态神经网络模型和基于重训练的神经网络模型进行了仿真。为了突出模型的可比性,采用相同的训练集来建立初始模型,从而体现各模型的优劣。为了验证模型的适应性,将与训练集同矿源的部分样本作为测试集,并将另一时段采集的不同矿源的数据加入作为测试集(共118组数据),也即采用相同的训练集与测试集进行仿真,得静态神经网络、基于重训练的网络和动态RBF网络的仿真结果分别如图4~图6所示,动态RBF神经网络隐含层节点变化如图7所示。
从图4可以看出,静态神经网络模型没有考虑对新增样本不适时的模型结构调整问题,当出现不一样的矿源时,模型无法对对象进行跟踪,出现模型失配的现象。
图5、图6表明基于重训练的自适应神经网络模型和动态神经网络模型都能对变矿源做出模型的合理调整,但是重训练模型是基于新入矿下的样本重训练得到的模型,虽能有效解决实际对象特性变化带来的模型失配问题,但每次重训练耗时较多,不适用于变化较频繁的实时系统。而动态神经网络模型是基于新增不适样本的调整修正,且过程中有许多阈值参数需要确定,主观性较大,模型好坏较依赖于人的经验。但在一定的精度允许下,其较简便的调整在实时系统中具有很大优势。
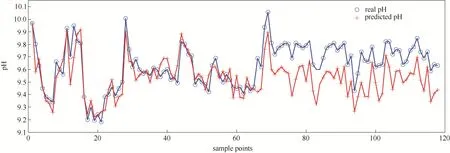
图4 静态神经网络模型仿真结果Fig.4 Simulation results of static neural network model

图5 基于重训练的自适应神经网络模型仿真结果Fig.5 Simulation results of adaptive neural network model based on weight training
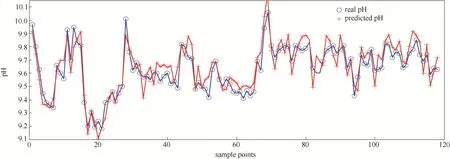
图6 动态RBF神经网络模型仿真结果Fig.6 Simulation results of dynamic RBF neural network model
从图7可以看出,隐含层节点在开始训练后一段时间内节点数不变,然后节点数增多,进而剔除低贡献率节点后有所下降并进入稳定状态,加入新工况之后,隐含层节点数有所增加,然后剔除合并节点后下降并恢复到稳定状态。
为了检验预测模型的优劣,考虑参数
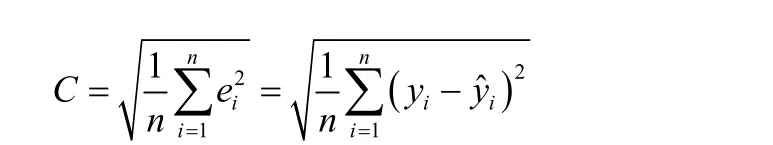
对各网络的均方根误差进行计算得到:静态RBF网络为0.142,基于重训练神经网络为0.0816,动态RBF网络为0.0713。可知整体性能上动态RBF最佳,对浮选过程的在线检测、工况判断和故障诊断等应用也具有相当大的优势。
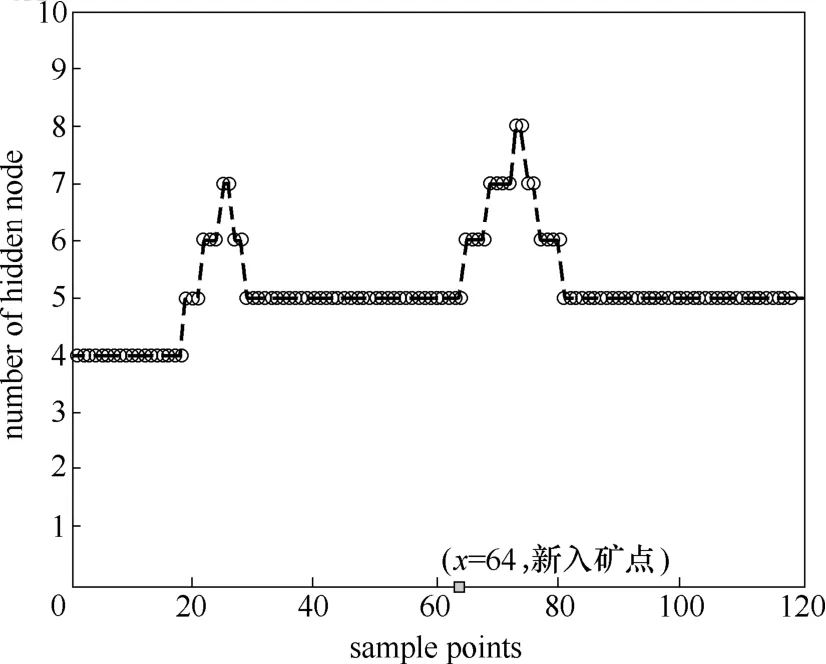
图7 动态RBF神经网络隐含层节点数目变化Fig.7 Number of hidden node of dynamic RBF neural network changing with samples
3 结 论
针对铝土矿浮选过程中矿源变化带来的工况状态迁移造成静态神经网络模型失配的问题,本文利用动态网络自身的特性动态地增删隐层节点以及修正网络参数,从而实现模型对对象的实时跟踪。最后通过实际生产数据仿真验证了该动态神经网络建模方法能解决矿源变化下模型失配的问题。同时,该建模方法还有待优化的问题,即部分经验值、阈值的选取方法并不是很完善,需要通过理论与实践对其进行深入的研究。
References
[1] 曹鹏飞, 罗雄麟. 化工过程软测量建模方法研究进展 [J]. 化工学报, 2013, 64 (3): 788-800.
CAO P F, LUO X L. Modeling of soft sensor for chemical process [J]. CIESC Journal, 2013, 64 (3): 788-800.
[2] MCBRIDE J, SULLIVAN A, XIA H, et al. Reconstruction of physiological signals using iterative retraining and accumulated averaging of neural network models [J]. Physiological Measurement, 2011, 32 (6): 661-675.
[3] YIN F, WANG H, XIE L, et al. Data driven model mismatch detection based on statistical band of Markov parameters [J]. Computers & Electrical Engineering, 2014, 40 (7): 2178-2192.
[4] 李翔宇, 高宪文,侯延彬. 基于在线动态高斯过程回归抽油井动液面软测量建模 [J]. 化工学报, 2015, 66 (6): 2150-2158.
LI X Y, GAO X W, HOU Y B. Online dynamic Gaussian process regression for dynamic liquid level soft sensing of sucker-rod pumping well [J]. CIESC Journal, 2015, 66 (6): 2150-2158.
[5] WALLACE M, TSAPATSOULIS N, KOLLIAS S. Intelligent initialization of resource allocating RBF networks [J]. Neural Networks, 2005, 18 (2): 117-122.
[6] GIANTOMASSI A, IPPOLITI G, LONGHI S, et al. On-line steam production prediction for a municipal solid waste incinerator by fully tuned minimal RBF neural networks [J]. Journal of Process Control, 2011, 21 (1): 164-172.
[7] SONG W, LIANG J Z, HE X L, et al. Taking advantage of improved resource allocating network and latent semantic feature selection approach for automated text categorization [J]. Applied Soft Computing, 2014, 21: 210-220.
[8] BACK A D, TSOI A C. FIR and IIR synapses, a new neural network architecture for time series modeling [J]. Neural Computation, 1991, 3 (3): 375-385.
[9] DELGADO A, KAMBHAMPATI C, WARWICK K. Dynamic recurrent neural network for system identification and control [J]. IEE Proceedings-Control Theory and Applications, 1995, 142 (4): 307-314.
[10] ZHANG Y, JIANG D, WANG J. A recurrent neural network for solving Sylvester equation with time-varying coefficients [J]. IEEE Transactions on Neural Networks, 2002, 13 (5): 1053-1063.
[11] ASH T. Dynamic node creation in back-propagation networks [J]. Connection Science, 1989, 1 (4): 365-375.
[12] BARTLETT E B. Dynamic node architecture learning: an information theoretic approach [J]. Neural Networks, 1994, 7 (1): 129-140.
[13] PLATT J. A resource-allocating network for function interpolation [J]. Neural Computation, 1991, 3 (2): 213-225.
[14] KADIRKAMANATHAN V, NIRANJAN M. A function estimation approach to sequential learning with neural networks [J]. Neural Computation, 1993, 5 (6): 954-975.
[15] LU Y, SUNDARARAJAN N, SARATCHANDRAN P. Performance evaluation of a sequential minimal radial basis function (RBF) neural network learning algorithm [J]. IEEE Transactions on Neural Networks, 1998, 9 (2): 308-318.
[16] 韩丽, 司风琪, 徐治皋. 改进的RAN网络及其在热工过程在线建模中的应用 [J]. 锅炉技术, 2004, 35 (5): 12-15.
HAN L, SI F Q, XU Z G. The improved RAN and its application in thermal processes modeling [J]. Boiler Technology, 2004, 35 (5): 12-15.
[17] 李彬. 一种改进的 RAN 学习算法 [J]. 模式识别与人工智能, 2006, 19 (2): 220-226.
LI B. An improvement of the RAN learning algorithm [J]. Pattern Recognition and Artificial Intelligence, 2006, 19 (2): 220-226.
[18] LI Y, SUNDARARAJAN N, SARATCHANDRAN P. Analysis of minimal radial basis function network algorithm for real-time identification of nonlinear dynamic systems [J]. IEEE Proceedings-Control Theory and Applications, 2000, 147 (4): 476-484.
研究论文
Received date: 2015-12-21.
Foundation item: supported by the National Natural Science Foundation of China (61304126, 61473318, 61134006, 61304019).
Dynamic RBF neural networks for model mismatch problem and its application in flotation process
WANG Xiaoli, HUANG Lei, YANG Peng, YANG Chunhua
(School of Information Science and Engineering, Central South University, Changsha 410083, Hunan, China)
Abstract:It is difficult to measure the process parameters online in the bauxite froth flotation process because the slurry deposits quickly. Especially, frequent change of the characteristics of the ore makes the process parameters change from time to time. So that, the static soft sensing models, such as the neural network model, which was obtained by a fixed set of training samples, may not track the dynamic characteristics of the process caused by change of the ore resource. And, thus, model mismatch problem occurs. In this paper, for model mismatch problem under various ore sources, dynamic RBF neural network modeling method based on the hidden layer node dynamic allocation and model parameters dynamic correction strategy is proposed. And the model is used for online measurement of the pH of the slurry in the flotation process, simulation results show that the dynamic model can solve the model mismatch problem well.
Key words:froth flotation process; dynamic RBF neural network; model mismatch; migration of working condition
DOI:10.11949/j.issn.0438-1157.20151940
中图分类号:TQ 027.1
文献标志码:A
文章编号:0438—1157(2016)03—0897—06
基金项目:国家自然科学基金项目(61304126,61473318,61134006,61304019)。
Corresponding author:WANG Xiaoli, xlwang@csu.edu.cn
