基于偏相关性分析的MPC控制器模型失配检测
2016-05-11李秋美田学民尚林源中国石油大学华东信息与控制工程学院山东青岛266580
李秋美,田学民,尚林源(中国石油大学(华东)信息与控制工程学院,山东 青岛 266580)
基于偏相关性分析的MPC控制器模型失配检测
李秋美,田学民,尚林源
(中国石油大学(华东)信息与控制工程学院,山东 青岛 266580)
摘要:在实际中,模型失配是导致模型预测控制性能下降的关键因素。传统的相关性分析方法在分析某一通道的预测残差和操作变量之间的相关性时,会受到其他操作变量及干扰的影响,导致结果不可靠,无法准确定位失配。针对上述问题,现采用偏相关性分析方法。在滤除其他操作变量和干扰影响的前提下,分析各通道预测残差和操作变量之间的相关性,将模型失配问题转化为一定区间上偏相关系数的分布问题。通过观察各通道偏相关系数的分布图判断是否发生失配,并通过Shell塔实验验证该方法的有效性。
关键词:模型失配;模型预测控制;相关性分析;偏相关性分析;实验验证
2015-12-11收到初稿,2015-12-25收到修改稿。
联系人:田学民。第一作者:李秋美(1990—),女,硕士研究生。
引 言
目前,以模型预测控制(MPC)为代表的先进控制策略在工业中得到了广泛应用。但实践中发现,MPC控制器在投入运行初期性能表现优越,运行一段时间后,其性能就会下降。因此,在过去几十年中,关于MPC性能监控、评价及诊断的研究引起了极大关注[1-3]。在实际的工业过程中,控制器参数整定不当、噪声干扰、模型失配、阀门黏滞、感知器偏差等都会影响控制回路的性能[4]。其中,模型失配是导致MPC性能下降的关键因素。因此,检测并隔离导致MPC控制器性能恶化的模型失配非常重要[5]。
近年来,关于模型失配检测的研究成果不断涌现。研究方法主要分为两大类:基于变量间关系的方法和基于系统辨识的方法。前者如单回路中的相关分析法诊断模型失配[6],多回路中的相关分析法[7]、偏相关分析方法[8-9]、基于逐步变量选择的方法[10]以及基于马尔科夫参数的方法[11]等来检测和定位模型失配通道。这些方法主要通过间接关系来检测失配存在与否。基于系统辨识的方法如利用常规闭环数据估计模型偏差的最小方差基准,评价模型质量[12-13]。根据新息模型自相关函数的阶次区分MPC中扰动和过程动态变化[14]。利用频率域的过程模型比辨识单入单出传递函数中的失配参数[15]。此外,基于状态空间模型,通过多个指标确定失配的参数矩阵组合[16-18]等。这类方法以具体的模型为基础,通常能与控制行为的变化联系起来。
在上述研究的基础上,本文基于偏相关性分析方法,研究动态矩阵控制(dynamic matrix control,DMC)下模型失配的检测问题。针对增益失配、时间常数失配和时滞失配3种情况分别进行研究,并在Shell塔上进行仿真实验。
1 问题描述

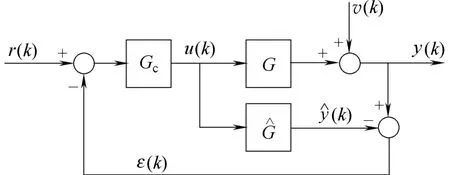
图1 内模控制结构Fig.1 Chart of internal model control
式中,Δ表征了预测残差ε与操作变量u之间的关系。因此,可以通过分析与之间的相关性来检测模型失配。若Δij为0,表明iε和uj不相关,该通道无失配发生;反之,则发生失配。此外,由图1可知
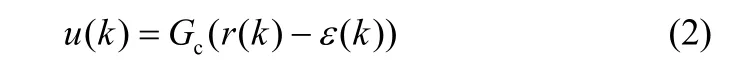
所以,由式(1)和(2)可得

若式(3)中,r( k ) = 0,则

此时,式(4)中不包含Δ的信息。说明在没有设定值激励的情况下,通过分析ε和u的关系无法判断模型是否失配。
另外,在实际中,被控对象大多是存在耦合的多输入多输出(multi-input-multi-output,MIMO)过程。不仅操作变量和被控变量间存在相关性,各操作变量之间也存在相互关联的现象,此外还有各种不可测干扰的影响。因此,采用传统相关性分析方法分析ε和u的关系进行模型失配检测,可能导致对失配的定位不准确。
2 偏相关性分析
偏相关性分析是在滤除其他变量影响的前提下,研究某两个变量之间相关性的统计分析方法。
假设变量Y受到变量X1, X2,… , Xn的影响,并且变量Xi( i= 1,… , n )间彼此相关。若分析变量Y和X1之间的偏相关性,可先建立回归方程,采用最小二乘法(least square,LS)进行参数辨识[8]。
首先,变量Y和X1用X2, X3,… , Xn线性表示为

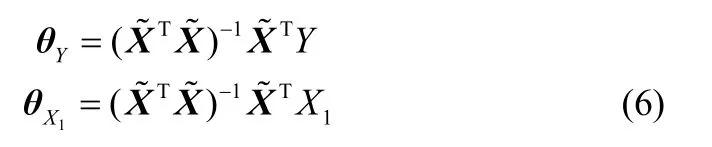
因此,模型的估计误差为

式中,eY和eX1表示变量Y和X1中不受影响的部分。因此,变量Y和X1之间的偏相关性分析等价于eY和eX1之间传统的相关性分析。从而,可以判断在不受其他变量影响时,变量Y和X1是否相关。变量Y和其他变量之间的偏相关性分析类似。
3 基于偏相关性分析的模型失配检测
利用ε和u间的偏相关性分析检测模型失配,步骤如下。
(1)在充分激励的条件下获取闭环过程数据。
(2)去除干扰对各操作变量的影响。
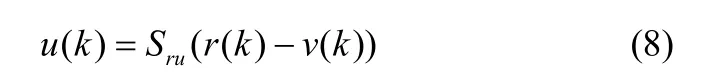

(3)去除各通道操作变量和预测残差中其他操作变量的影响。以通道为例。
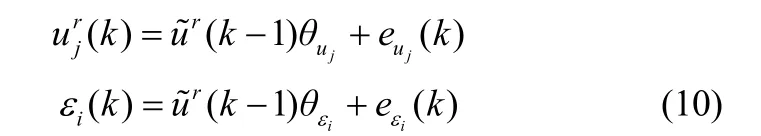
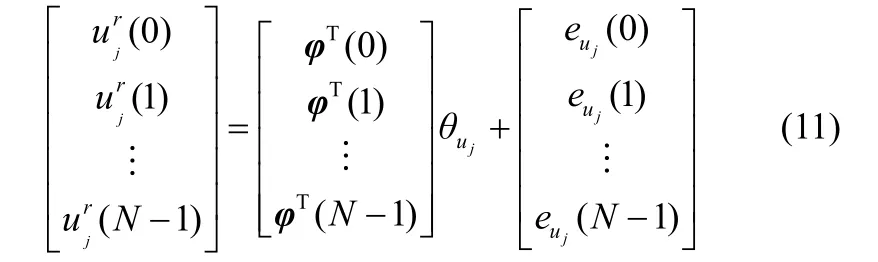
式(11)可以简化为

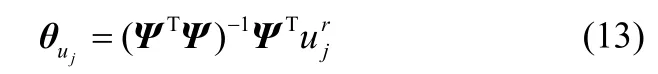
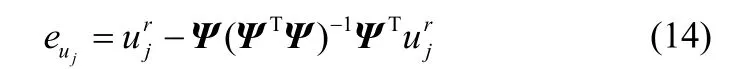
从而
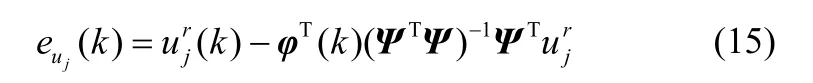
同理可得
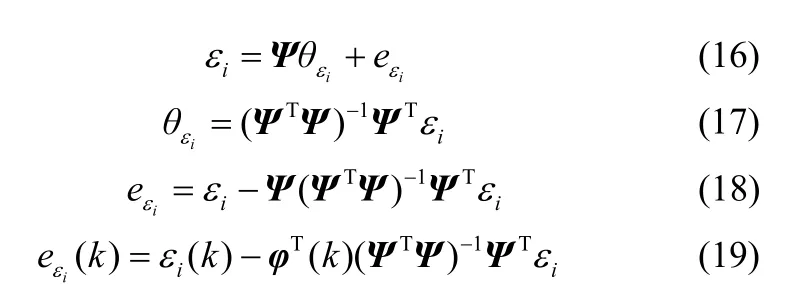
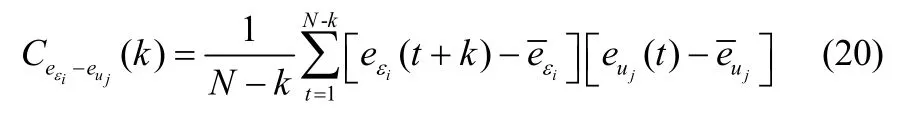
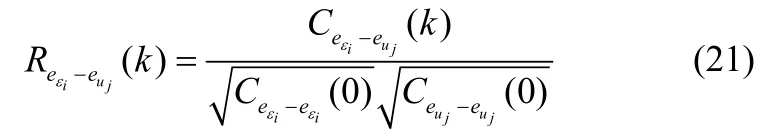
4 仿真实验
以Shell重油分馏塔作为研究对象,该塔是个典型的具有大纯滞后的MIMO过程。输出y1、y2、 y3分别表示塔的顶部测量点、侧部测量点和底部回流温度。操作变量u1、u2、u3分别表示顶部抽出、侧线抽出和底部回流。过程模型为

各个通道的干扰模型为
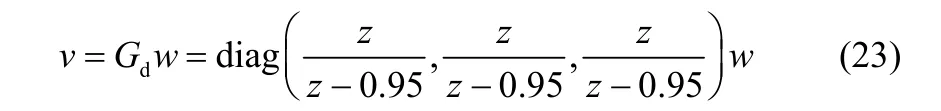
其中,w是零均值的白噪声,协方差矩阵为∑w=diag(0.012,0.012,0.012)。
将过程模型离散化,采样时间为1 min。设计DMC控制器,预测时域P =30,控制时域M =5,控制权矩阵Q= I,误差权矩阵M=0.5 I,对操作变量幅值约束为(− 10,+10)。设定值激励采用幅值为0.5,奈奎斯特频率为0.1的PRBS信号。
4.1 确定互相关系数的邻域
实际中,白噪声是不存在的。即使两个随机变量完全相互独立,其互相关系数也不会严格为0,而是以0为中心上下波动[20]。为了便于实际应用,需界定互相关系数R的邻域。当R值都在该范围内时,两个序列不相关,否则认为相关。
通过仿真产生1000对服从N(0,1)分布的白噪声,计算每对白噪声互相关系数的最值,结果如图2所示。由图2可知,互相关系数的最值在±0.15左右。因此,R的邻域为(− 0.15,+ 0.15)。

图2 互相关系数最值Fig.2 Maxima and minima of cross-correlation coefficients
4.2 模型失配检测
仿真研究4种不同的模型失配类型,具体参数设置见表1。其中,S1表示G11、G12、G21通道的增益均增大25%;S2表示G11、G21、G31通道的时滞均增大4个时间单位;S3表示G31、G32、G33通道的时间常数均减小30%;S4表示各通道均引入10%的时间常数失配的情况下,G11另引入50%的增益失配。
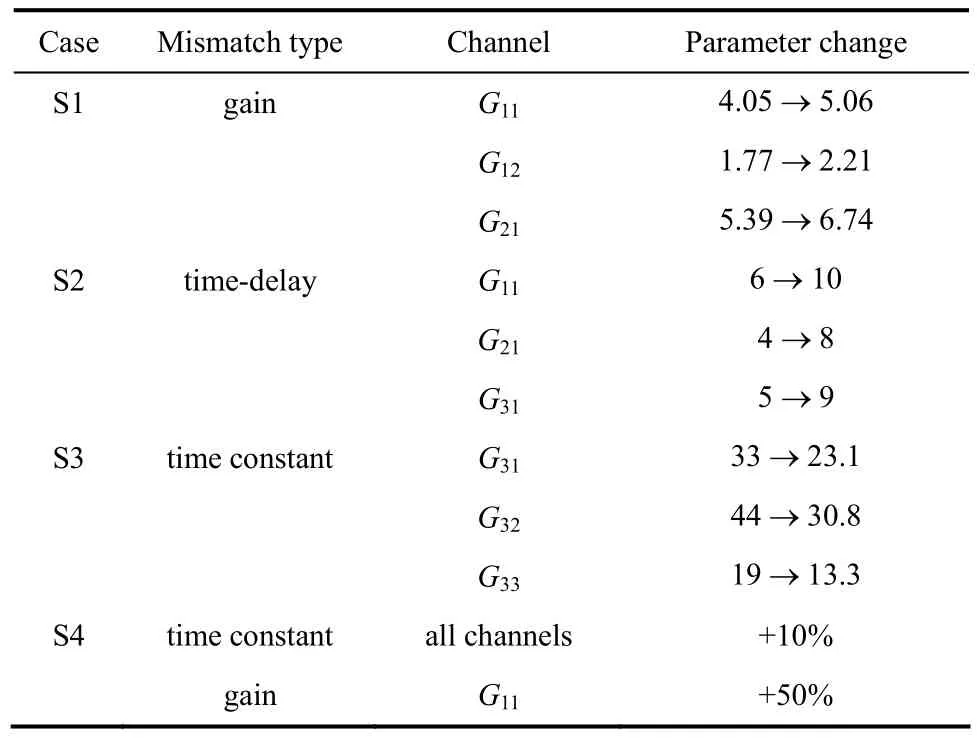
表1 模型失配设置Table 1 Set of model-mismatch
S1-增益失配情况下,偏相关性分析方法的检测结果如图3(a)所示。同种情况下,利用传统的相关性分析方法,即直接计算未经处理的uj和iε之间的互相关系数,如图3(b)所示。

图3 增益失配对比Fig.3 Comparison chart of gain mismatch
由图3(a)可以看出,G11、G12、G21通道的偏相关系数均超限,而其他通道的偏相关系数皆在邻域内。因此,该情况下,偏相关性分析能够准确检测并定位失配通道。而图3(b)相关性分析方法的检测结果中,与1ε、2ε有关通道的相关系数均超限,无法准确检测和定位失配位置。
S2-时滞失配的情况下,偏相关性分析方法和传统的相关性分析方法检测结果如图4所示。
由图4(a)可知,G11、G21、G31通道的偏相关系数均严重超限,而其他通道皆不受影响。因此,对失配的检测与定位是准确的。图4(b)中,与1ε、2ε、3ε有关通道的相关系数均有不同程度的超限,得到与图3(b)相似的结果。
S3-时间常数失配的情况下,偏相关性分析方法的检测结果如图5所示。
图5中,G31、G32、G33通道的偏相关系数均超限,而其他通道皆在偏相关系数的邻域内,检测结果与起初的失配参数设置相符。
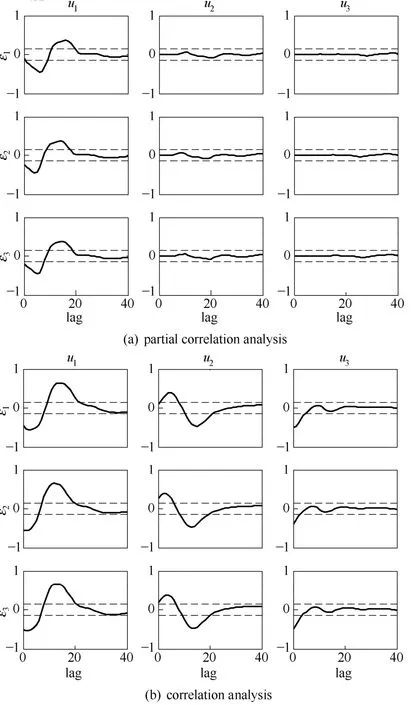
图4 时滞失配对比Fig.4 Comparison chart of time-delay mismatch
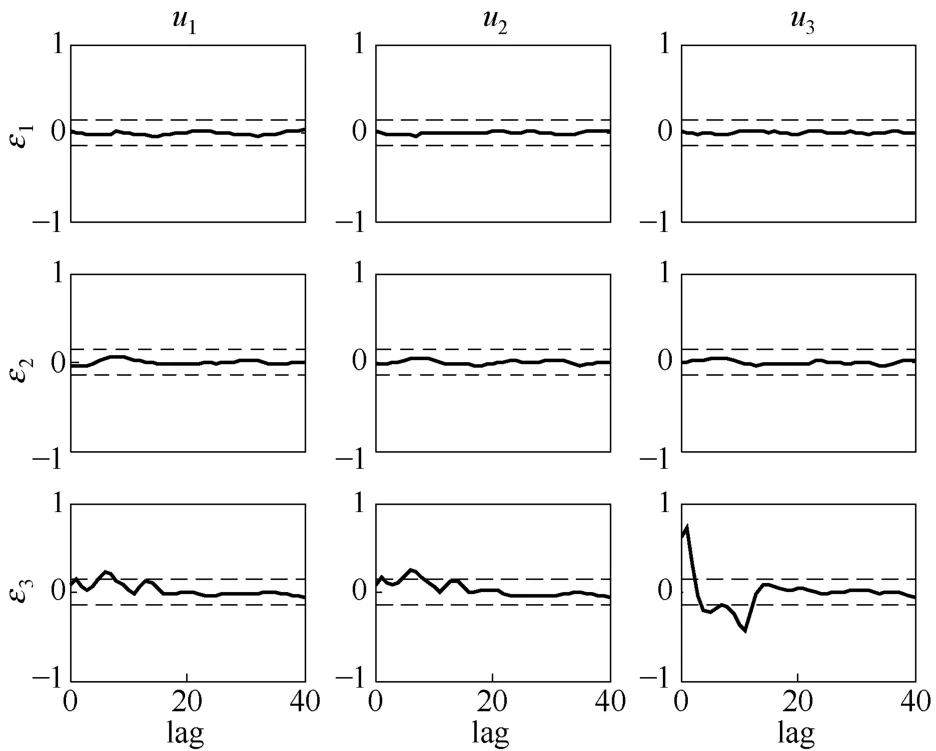
图5 时间常数失配时偏相关性分析Fig.5 Partial correlation analysis chart of time constant mismatch
S4情况下,即增益和时间常数均失配时,偏相关性分析方法的检测结果见图6。图6中,G11通道的失配情况较其他通道更为严重,偏相关系数明显超限。说明偏相关性分析方法能够区分众多失配通道中失配较为严重的通道。
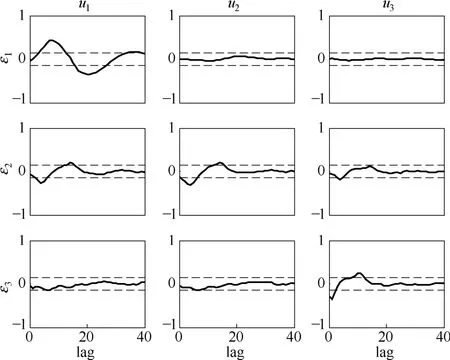
图6 偏相关性分析Fig.6 Partial correlation analysis chart
5 结 论
本文针对传统相关性分析在检测多输入多输出过程的模型失配时存在的不足,引入了偏相关性分析方法。通过分析各通道预测残差和操作变量间的偏相关性检测模型失配。在Shell塔上的仿真实验表明,与传统的相关性分析方法相比,该方法不仅能够准确地检测及定位失配通道,还能够在一定程度上识别出失配的严重程度,对后期模型失配的处理提供指导依据。
References
[1] HARRIS T J. Assessment of closed-loop performance [J]. The Canadian Journal of Chemical Engineering, 1989, 67 (10): 856-861. [2] YU J, QIN S J. Statistical MIMO controller performance monitoring(Ⅰ): Data-driven covariance benchmark [J]. Journal of Process Control, 2008, 18 (3/4): 277-296.
[3] YU J, QIN S J. Statistical MIMO controller performance monitoring(Ⅱ): Performance diagnosis [J]. Journal of Process Control, 2008, 18 (3/4): 297-319.
[4] 张巍, 王昕, 王振雷. 基于证据网络的多变量MPC经济性能评估[J]. 化工学报, 2012, 63 (11): 3585-3590.
ZHANG W,WANG X,WANG Z L. Economic performance assessment of multivariable MPC based on evidential network [J]. CIESC Journal, 2012, 63 (11): 3585-3590.
[5] BADWE A S, PATWARDHAN R S, SHAH S L, et al. Quantifying the impact of model-plant mismatch on controller performance [J]. Journal of Process Control, 2010, 20 (4): 408-425.
[6] STANFELJ N, MARLIN T E, MACGREGOR J F. Monitoring and diagnosing process control performance: the single-loop case [J]. Industrial & Engineering Chemistry Research, 1993, 32 (2): 301-314.
[7] WEBBER J R, GUPTA Y P. A closed-loop cross-correlation method for detecting model mismatch in MIMO model-based controllers [J]. ISA Transactions, 2008, 47 (4): 395-400.
[8] BADWE A S, GUDI R D, PATWARDHAN R S, et al. Detection of model-plant mismatch in MPC applications [J]. Journal of Process Control, 2009, 19 (8): 1305-1313.
[9] CARLSSON R. A practical approach to detection of plant model mismatch for MPC [D]. Sweden: Linköping University, 2010.
[10] KANO M, SHIGI Y, HASEBE S, et al. Detection of significant model-plant mismatch from routine operation data of model predictive control system[C]//9th International Symposium on Dynamics and Control of Process Systems. Belgium: IFAC, 2010: 685-690.
[11] WANG H, SONG Z H, XIE L. Parametric mismatch detection and isolation in model predictive control system[C]//8th IFAC International Symposium on Advanced Control of Chemical Processes. Singapore, 2012: 154-159.
[12] SUN Z J, QIN S J, SINGHAL A, et al. Control performance monitoring via model residual assessment[C]//American Control Conference (ACC). IEEE, 2012: 2800-2805.
[13] SUN Z J, QIN S J, SINGHAL A, et al. Performance monitoring of model-predictive controllers via model residual assessment [J]. Journal of Process Control, 2013, 23 (4): 473-482.
[14] HARRISON C A, QIN S J. Minimum variance performance map for constrained model predictive control [J]. Journal of Process Control, 2009, 19 (7):1199-1204.
[15] SELVANATHAN S, TANGIRALA A K. Diagnosis of poor control loop performance due to model-plant mismatch [J]. Industrial and Engineering Chemistry Research, 2010, 49 (9): 4210-4229.
[16] 陈贵, 杨江, 谢磊, 等. 基于子空间方法的模型失配检测研究 [J].化工学报, 2011, 62 (9): 2575-2581.
CHEN G, YANG J, XIE L, et al. Research on model-plant mismatch detection based on subspace approach [J]. CIESC Journal, 2011, 62 (9): 2575-2581.
[17] JIANG H, LI W, SHAH S L. Detection and isolation of model-plant mismatch for multivariate dynamic systems[C]//IFAC Symposium on Fault Detection, Supervision and Safety of Technical Processes. 2006, 6: 1396-1401.
[18] CHEN J Y, Y J, MORI J. Closed-loop subspace projection based state-space model-plant mismatch detection and isolation for MIMO MPC performance monitoring [C]//Decision and Control (CDC). 2013: 6143-6148.
[19] LOEFF M V, KURAMOTO A S R, GARCIA C. Enhancements of plant-model mismatch detection methods in MPC using partial correlation [C]//Anais do XX Congresso Brasileiro de Automática Belo Horizonte. MG, 2014.
[20] 梁腾伟.多变量预测控制系统模型失配评价方法研究[D].杭州: 浙江大学, 2008.
LIANG T W. Model mismatch assessment of multivariate model predictive control [D]. Hangzhou: Zhejiang University, 2008.
研究论文
Received date: 2015-12-11.
Foundation item: supported by the National Natural Science Foundation of China (61273160, 61403418) and the Fundamental Research Funds for the Central Universities (15CX06063A).
Detection of model-plant mismatch based on partial correlation analysis of MPC controllers
LI Qiumei, TIAN Xuemin, SHANG Linyuan
(College of Information and Control Engineering, China University of Petroleum (East China), Qingdao 266580, Shandong, China)
Abstract:In practice, model-plant mismatch(MPM) is a key factor that results in performance deterioration in model predictive control(MPC). Traditional correlation analysis between the prediction residual and the manipulated variable of a channel is usually affected by other manipulated variables and disturbance. The result of this process is unreliable, thus unable to locate the MPM accurately. Based on the above problems, partial correlation analysis is used to calculate the correlation between the prediction residual and the manipulated variable of each channel, under the premise of removing the effect of other manipulated variables and disturbance. The MPM problem is converted to a distribution problem of partial correlation coefficients in a certain interval. Whether a channel is mismatched is judged by observing the distribution graph of partial correlation coefficients. The experimental validation on the Shell tower demonstrates the effectiveness of this method.
Key words:model-plant mismatch; model predictive control; correlation analysis; partial correlation analysis; experimental validation
DOI:10.11949/j.issn.0438-1157.20151883
中图分类号:TP 277
文献标志码:A
文章编号:0438—1157(2016)03—0852—06
基金项目:国家自然科学基金项目(61273160,61403418);中央高校基本科研业务费专项资金项目(15CX06063A)。
Corresponding author:Prof. TIAN Xuemin, tianxm@upc.edu.cn
