基于KSFDA-SVDD的非线性过程故障检测方法

张汉元，田学民（中国石油大学（华东）信息与控制工程学院， 山东 青岛 266580）



基于KSFDA-SVDD的非线性过程故障检测方法

张汉元，田学民
（中国石油大学（华东）信息与控制工程学院， 山东 青岛 266580）

摘要：慢特征分析（SFA）是一种无监督的线性学习算法，没有考虑过程数据的类别信息和非线性特征。针对此问题，提出一种基于核慢特征判别分析（KSFDA）和支持向量数据描述（SVDD）的非线性过程故障检测方法KSFDA-SVDD。该方法首先利用核技巧将数据从原始空间映射到高维空间，然后通过最大化正常工况数据和故障模式数据之间伪时间序列的时间变化同时最小化正常工况数据内部伪时间序列的时间变化计算判别矩阵，最后利用SVDD描述采用判别矩阵降维后的正常工况数据的分布域，构建监控统计量检测过程故障。在连续搅拌反应器（CSTR）过程上的仿真结果表明所提出方法的故障检测性能优于传统的KPCA方法。

关键词：慢特征分析；判别分析；支持向量数据描述；非线性过程；故障检测

2015-12-10收到初稿，2015-12-19收到修改稿。

联系人：田学民。第一作者：张汉元（1991—），男，博士研究生。

引 言

近年来，基于数据驱动的过程监控方法逐渐成为过程监控领域中的研究热点，其中主元分析（PCA）、偏最小二乘（PLS）和独立元分析（ICA）等是研究较多的方法[1-3]。研究者们围绕工业过程的非线性特征，提出了一系列改进的非线性PCA方法[4-5]。与其他的非线性方法相比，核主元分析法（KPCA）[5]使用核技巧计算非线性主元，不承担任何非线性的优化问题。但是KPCA是一种无监督的学习方法，它仅仅根据正常工况数据建立统计模型而无法利用历史故障数据的信息。因此在过程监控时，KPCA不能从历史故障数据中提取出重要的故障判别信息[6-7]。

慢特征分析（SFA）能够从快速变化的输入信号中提取出变化较慢的特征，它作为一种新的数据特征提取方法受到广泛关注[8]。文献[9-10]应用SFA提取不变特征解决模式分类和图像处理问题。考虑到数据的非线性特征，Bohmer等[11]采用核技巧构建非线性SFA方法。在SFA的基础上，Huang等[12]提出一种无监督的非线性近邻保持算法，保持原始空间中近邻点之间的距离在投影空间中尽可能小。为了同时考虑同类数据的相似性和不同类数据的差异性，文献[13-14]在SFA方法中引入了监督学习的思想。

为了从非线性数据中提取不变特征同时保持数据的类判别信息，本文提出基于核慢特征判别分析和支持向量数据描述（KSFDA-SVDD）的故障检测方法。从正常工况数据集和故障模式数据集中提取出判别矩阵后，利用判别矩阵对正常工况数据降维，采用SVDD描述降维后正常工况数据的分布域，建立监控指标检测故障。以连续搅拌反应器（CSTR）过程为对象对所提方法的有效性进行了验证。

1 慢特征分析

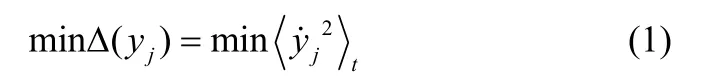
约束函数

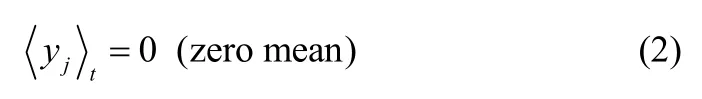
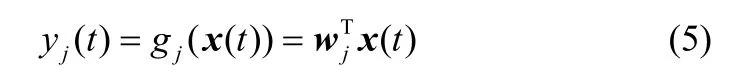
通常情况下，原始的输入数据在预处理阶段会进行归一化处理，因此约束函数（2）自动满足。目标函数（1）和约束函数（3）重新表述为

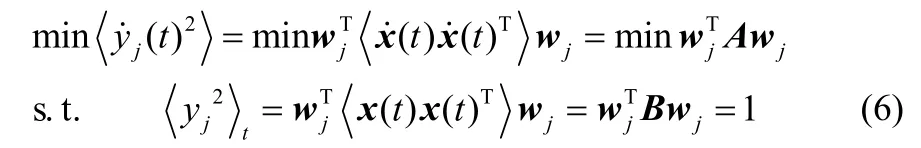
求解式（7）中的广义特征值问题获得式（6）的解。

对于非线性数据的情况，非线性SFA首先将输入数据非线性映射到高维特征空间，然后在特征空间中实施线性SFA变换。

2 KSFDA-SVDD故障检测方法

2.1 核慢特征判别分析

受到将数据的类判别信息融入到SFA中思想的启发[15]，本文提出核慢特征判别分析（KSFDA）方法，在高维特征空间中采用K-近邻方法构造类内和类间伪时间序列，根据最小化类内伪时间序列的时间变化同时最大化类间伪时间序列的时间变化准则求解判别矩阵。

考虑到数据的非线性特点，采用非线性映射函数Φ(⋅)分别将S和N映射到高维特征空间。用矩阵Sφ和Nφ分别表示特征空间中的故障模式数据集和正常工况数据集。

对于Nφ中的每一个数据点在中与近邻的k个数据点表示为对于中的数据点与远邻的p个数据点表示为。

为了尽可能多地保持类判别信息，KSFDA的优化目标是最大化正常工况数据φN和故障模式数据φ

S间伪时间序列的时间变化同时最小化正常工况数据φ

N内伪时间序列的时间变化

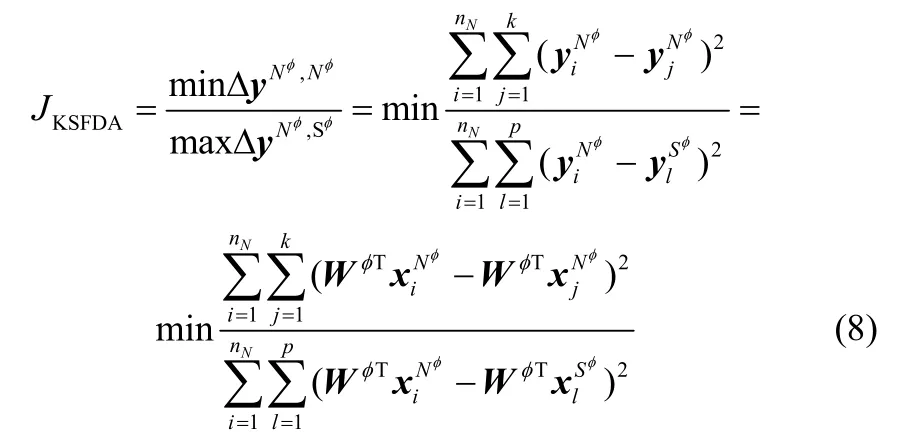
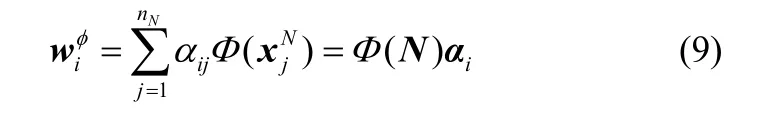
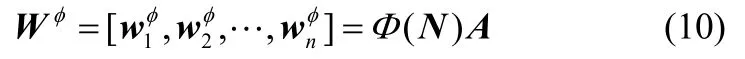
将式（10）代入式（8），获得

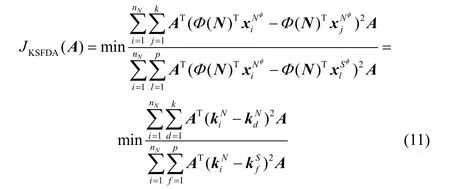
在本文中，核函数选择使用高斯核函数

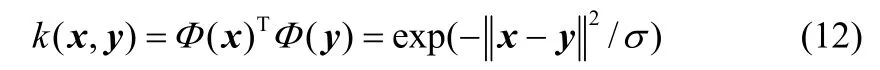
其中，σ表示核宽度参数。

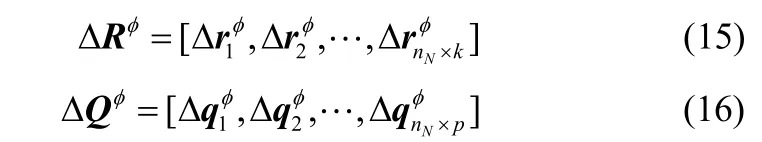
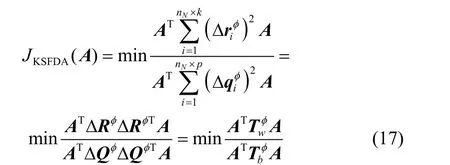
式（17）中的最小化问题可以转换成以下的广义特征值分解问题

2.2 支持向量数据描述

支持向量数据描述（SVDD）的基本思想是寻找一个最小体积的超球体包含全部或绝大部分的训练数据[16]。在本文中，使用SVDD监控正常工况数据的投影矩阵Y中数据的分布，构建监控统计量检测故障。对于正常数据的投影矩阵，SVDD解决以下的最优化问题

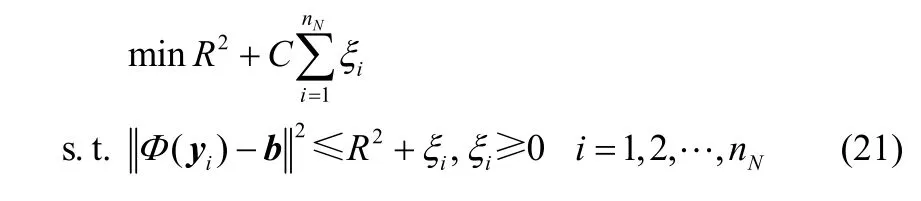
其中，b是超球体的球心，C是超球体的体积和误差数量之间的权衡因子。iξ是松弛因子，它表示一些训练样本被错误分类的概率。

应用拉格朗日乘子法后，SVDD优化问题的对偶形式如下

判定测试点xt是否是故障样本，计算其投影向量yt到球心b的距离D作为监控统计量

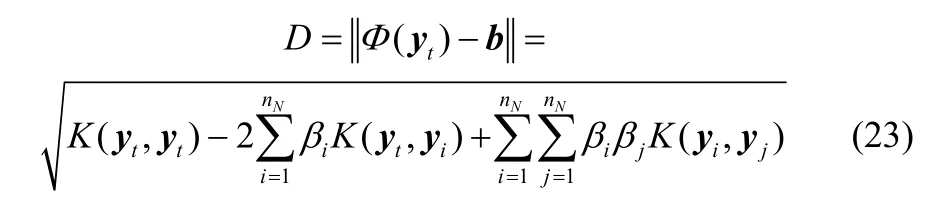
监控统计量D的控制限Dlimt定义为球面上任何支持向量到球心b的距离。如果则判定测试点xt是正常样本点，如果则判定测试点xt是故障样本点。

2.3 KSFDA-SVDD故障检测步骤

（1）离线建模阶段

② 对标准化后的数据集N和S采用高斯核函数变换到高维特征空间，获得数据集。

④ 根据式（19）计算高维空间中正常工况数据的投影矩阵Y，采用SVDD描述Y中数据的分布，建立监控统计量的控制限Dlimt。

（2）在线检测阶段

① 将当前测试数据xt进行标化后变换到高维特征空间，采用式（20）计算投影向量yt。

② 将投影向量yt代入式（23）计算当前监控统计量D，与控制限Dlimt比较，判断是否出现故障。

3 仿真分析

本文以连续搅拌反应釜（CSTR）系统作为仿真研究对象，其结构图参考文献[17]。在CSTR的仿真过程中加入服从高斯分布的测量噪声，采集900个正常工况下的样本。模拟7类故障的发生，在每一类故障中分别采集300个样本点，故障类型见表1。测试集数据采集900个样本点，在第201个采样时刻添加故障。

表1 故障类型Table 1 Fault pattern of CSTR system

在KPCA中，选取主元模型的阶数依据主元方差的贡献率在95%以上的原则，选用99%的置信上限来确定监控统计量2T和SPE的阈值，选取核参数σ=90。为了公平比较，在KSFDA-SVDD中选择矩阵A中特征向量的个数n与KPCA的主元个数一致，同样选取σ=90，近邻点个数k和远邻点个数p均取为6。

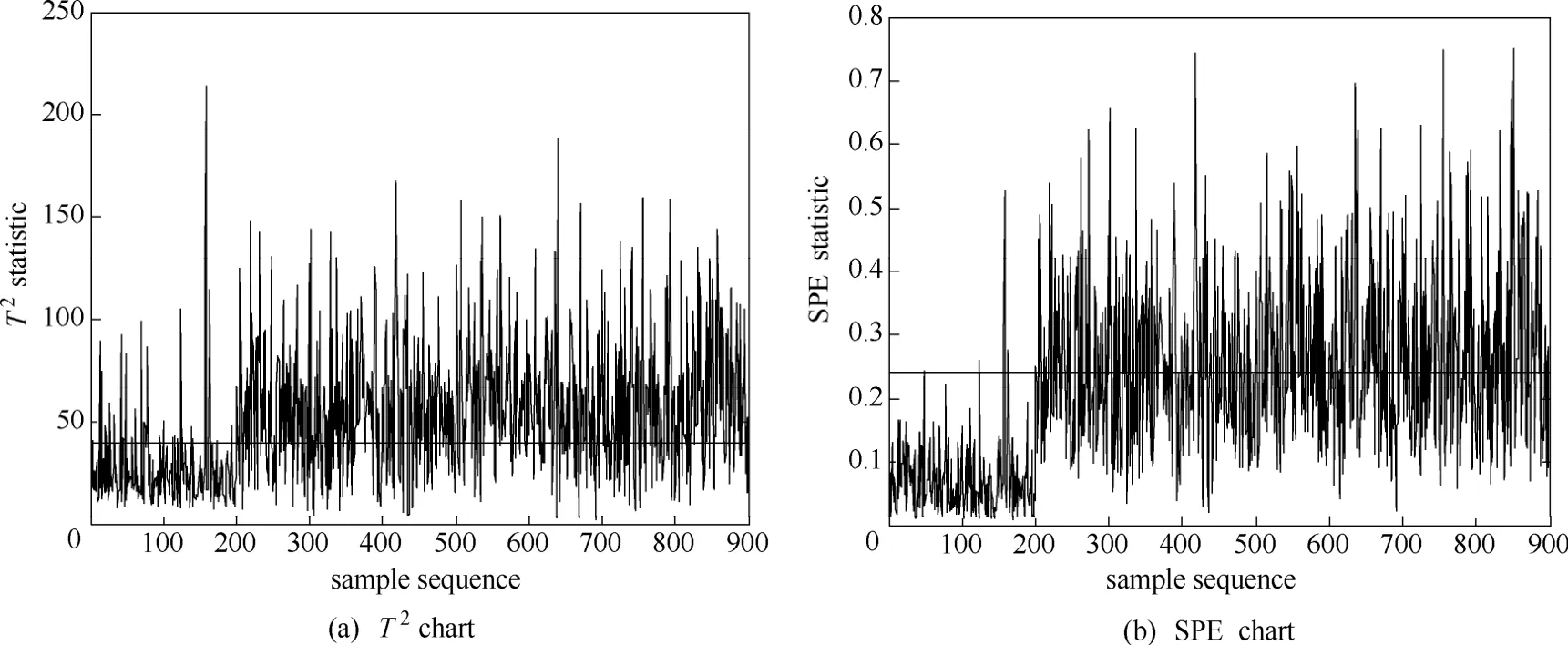
图1 KPCA对故障F3的监控图Fig.1 KPCA monitoring chart for Fault F3

故障F3为冷却水调节阀出现阶跃故障，KPCA 和KSFDA-SVDD的故障检测效果见图1和图2。在图1中，KPCA的2T和SPE监控统计量在各自的控制限上下波动，不能有效地检测出故障。在图2中，KSFDA-SVDD方法的D统计量在第201个采样点处检测出故障，故障检出率为100%。

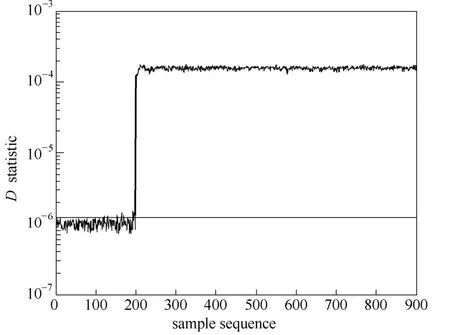
图2 KSFDA-SVDD对故障F3的监控图Fig.2 KSFDA-SVDD monitoring chart for Fault F3

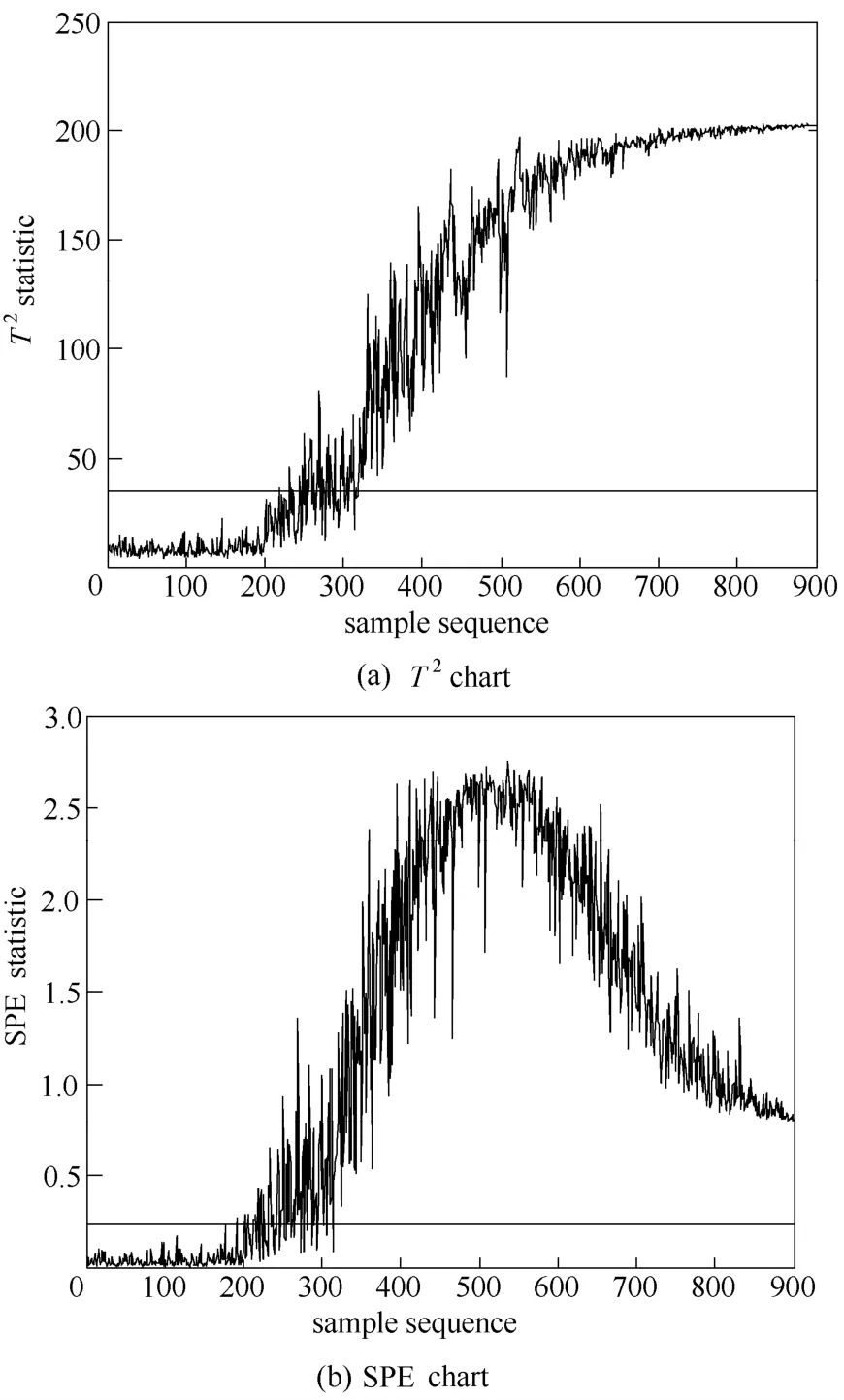
图3 KPCA对故障F6的监控图Fig.3 KPCA monitoring chart for Fault F6

故障F6为进料温度斜坡上升，图3显示KPCA 的SPE统计量在第266个采样点检测出故障，然而T2统计量在第307个采样点检测出故障，监控结果相对较差。在图4中，KSFDA-SVDD的D统计量在第209个采样点检测出故障。通过近一步的分析，KPCA的T2和SPE统计量故障检出率分别为83.31%和84.60%，KSFDA-SVDD的D统计量故障检出率为97.86%。

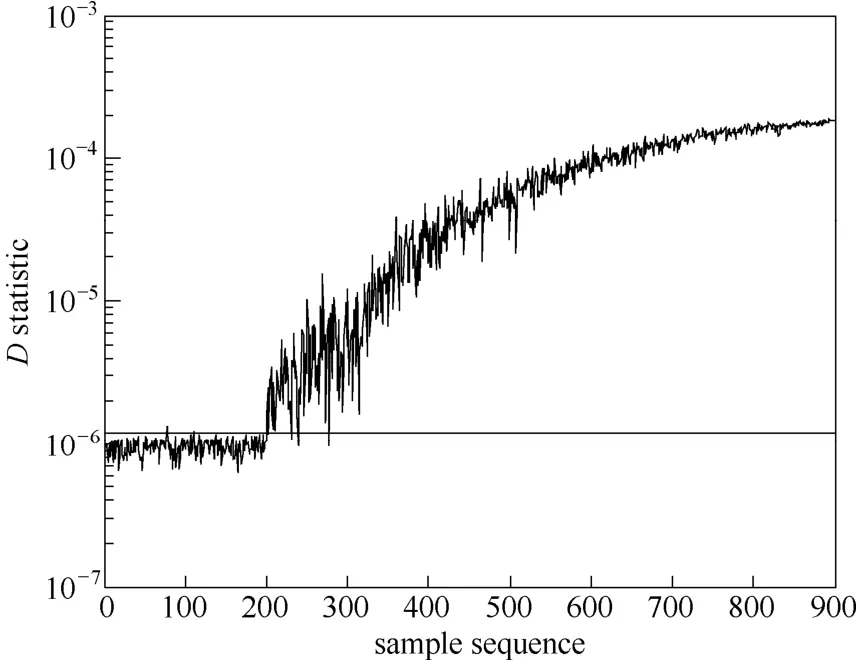
图4 KSFDA-SVDD对故障F6的监控图Fig.4 KSFDA-SVDD monitoring chart for Fault F6

表2给出了KPCA和KSFA-SVDD方法对7种故障的检测率。KPCA方法对于阶跃故障F3的故障检出率较低，不到50%，对于斜坡故障F1、F5、F6和F7的故障检出率在85%左右。而KSFA-SVDD方法对于所有阶跃故障的故障检出率均为100%，对于所有斜坡故障的故障检出率均在90%以上。综合以上分析，本文提出的KSFA-SVDD方法故障检测效果明显优于KPCA方法。

表2 KPCA和KSFDA-SVDD的故障检出率Table 2 Fault detection rate of two methods

4 结 论

本文提出了基于KSFDA-SVDD的非线性过程故障检测方法。KSFDA将正常工况数据和故障模式数据的类判别信息融入到SFA中并利用核技巧处理过程数据的非线性特征。利用从KSFDA方法

中求出的判别矩阵对正常工况数据降维后，采用SVDD描述正常数据的分布域，建立监控统计量。通过在CSTR过程上进行仿真证明所提出算法的故障检测效果优于传统的KPCA方法。

References

[1] GARCIA-ALVAREZ D, FUENTE M J, SAINZ G I. Fault detection and isolation in transient states using principal component analysis [J]. Journal of Process Control, 2012, 22 (3): 551-563.

[2] QIN S J. Survey on data-driven industrial process monitoring and diagnosis [J]. Annual Reviews in Control, 2012, 36 (2): 220-234.

[3] CAI L F, TIAN X M, CHEN S. A process monitoring method based on noisy independent component analysis [J]. Neurocomputing, 2014, 127 (3): 231-246.

[4] GENG Z Q, ZHU Q X. Multiscale nonlinear principal component analysis and its application for chemical process monitoring [J]. Industrial and Engineering Chemistry Research, 2005, 44 (10): 3585-3593.

[5] NGUYEN V H, GOLINVAL J C. Fault detection based on kernel principal component analysis [J]. Engineering Structures, 2010, 32 (11): 3683-3691.

[6] ZHAO C H, GAO F R. Fault-relevant principal component analysis (FPCA) method for multivariate statistical modeling and process monitoring [J]. Chemometrics and Intelligent Laboratory Systems, 2014, 133 (6): 1-16.

[7] ZHANG Y W, ZHANG L J, ZHANG H L. Fault detection for industrial processes [J]. Mathematical Problems in Engineering, 2012, 2012 (1): 1-18.

[8] WISKOTT L, SEJNOWSKI T J. Slow feature analysis: unsupervised learning of invariances [J]. Neural Computation, 2002, 14 (4): 715-770.

[9] WISKOTT L. How to solve classification and regression problems on high-dimensional data with a supervised extension of slow feature analysis [J]. The Journal of Machine Learning Research, 2013, 14 (1): 3683-3719.

[10] WU C, DU B, ZHANG L. Slow feature analysis for change detection in multispectral imagery [J]. IEEE Transactions on Geoscience and Remote Sensing, 2014, 52 (5): 2858-2874.

[11] BOHMER W, GRUNEWALDER S, NICKISCH H, et al. Regularized sparse kernel slow feature analysis[C]//Proceedings of the 2011 European Conference on Machine Learning and Knowledge Discovery in Databases. Athens, 2011: 235-248.

[12] HUANG Y P, ZHAO J L, LIU Y H, et al. Nonlinear dimensionality reduction using a temporal coherence principle [J]. Information Science, 2011, 181 (16): 3284-3307.

[13] ZHANG Z, TAO D. Slow feature analysis for human action recognition [J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2012, 34 (3): 436-450.

[14] ZHANG H Y, TIAN X M, CAI L F. Nonlinear process fault diagnosis using kernel slow feature discriminant analysis[C]//The 9th IFAC Symposium on Fault Detection, Supervision and Safety for Technical Processes. Paris, 2015, 48 (21): 607-612.

[15] HUANG Y P, ZHAO J L, TIAN M, et al. Slow feature discriminant analysis and its application on handwritten digit recognition[C]// Proceedings of International Joint Conference on Neural Networks. Atlanta, 2009: 1294-1297.

[16] SRIVASTAVA C. Support vector data description [J]. Machine Learning, 2004, 54 (1): 45-66.

[17] CAI L F, TIAN X M. A new fault detection method for non-Gaussian process based on robust independent component analysis [J]. Process Safety and Environmental Protection, 2014, 92 (6): 645-658.

研究论文

Received date: 2015-12-10.

Foundation item: supported by the National Natural Science Foundation of China (61273160, 61403418), the Natural Science Foundation of Shandong Province (ZR2014FL016) and the Fundamental Research Funds for the Central Universities (14CX06132A).

Nonlinear process fault detection based on KSFDA and SVDD

ZHANG Hanyuan, TIAN Xuemin
(College of Information and Control Engineering, China University of Petroleum (East China), Qingdao 266580, Shandong, China)

Abstract:Slow feature analysis (SFA) is an unsupervised liner learning algorithm and lacks the ability to consider class label information and data nonlinearity. In order to solve this problem, a novel nonlinear process fault detection method is proposed based on kernel slow feature discriminant analysis and support vector data description (KSFDA-SVDD). Firstly, process data is mapped from the original space into a high dimension feature space via kernel trick. Then, the discriminant matrix that maximizes the temporal variation of between-class pseudo-time series and minimizes the temporal variation of within-class pseudo-time series simultaneously is calculated. Finally, SVDD is applied to describe the distribution region of normal operation data which is projected to the discriminant matrix and one monitoring index is constructed to indicate the occurrence of the abnormal event. Simulation results on the continuous stirring tank reactor (CSTR) process show that the proposed method is more effective than the traditional KPCA method in terms of detecting faults.

Key words:slow feature analysis; discriminant analysis; support vector data description; nonlinear process; fault detection

DOI：10.11949/j.issn.0438-1157.20151875

中图分类号：TP 277

文献标志码：A

文章编号：0438—1157（2016）03—0827—06

基金项目：国家自然科学基金项目（61273160，61403418）；山东省自然科学基金项目（ZR2014FL016）；中央高校基本科研业务费专项资金（14CX06132A）。

Corresponding author:Prof. TIAN Xuemin, tianxm@upc.edu.cn