基于转化思想，探求一题多解

☉上　海　市　岭　南　中　学　刘华为☉浙江省衢州市柯城区石梁中学　余利英



基于转化思想，探求一题多解

☉上海市岭南中学刘华为
☉浙江省衢州市柯城区石梁中学余利英

由于一题多解既可激发学习兴趣、理清知识脉络、深化认知层次、提高课堂效率，又对培养学生思维的发散性、灵活性、深刻性和创新性大有裨益，因而深受广大同仁的偏爱.那么如何才能探求一题多解呢？本文试图基于转化思想，从知识溯源、转换视角和分类表述等角度对一题多解的生成谈几点拙见，以求抛砖引玉.

一、题目呈现

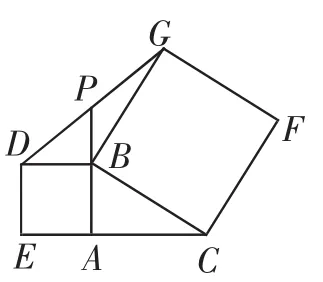
图1

如图1，已知△ABC中，∠BAC= 90°，四边形ABDE、BCFG是两个正方形，AB的延长线交DG于点P，求证：AC=2BP.

二、解法展示

一般地，数学习题是由课本的有关知识、信息、符号，通过迁移、发散和综合而来的，因此，相关问题的知识源就是解决问题的最佳策略和一题多解的知识自然生成点.

1.利用线段中点定义证明

证法1：如图2，延长BP至点Q，使BQ=AC.欲证BQ= 2BP，易想到连接GQ，可利用证明△BPD≌△QPG得BP= QP.为此需证明∠Q=90°且GQ=DB= BA，即证明△ABC≌△QGB.

由同角（∠ABC）的余角相等，可得∠ACB=∠QBG，再根据“边角边”可知△ABC和△QGB确实全等，故问题得证.

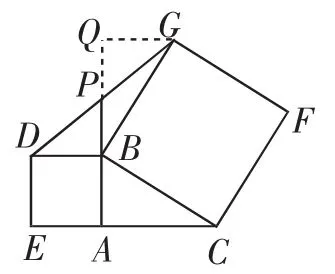
图2

证法2：当然图2的辅助线也可表述为“过点G作GQ⊥BP，交BP的延长线于点Q”，则依据“角角边”可证△ABC≌△QGB，得AC=QB且GQ=BA=DB.根据“角角边”或“角边角”可证△BPD≌△QPG，得BP=QP，所以AC= BQ=2BP.

证法3：图2的辅助线还可表述为“过点G作GQ∥BD，交BP的延长线于点Q”，则∠GQB=∠QBD=∠BAC= 90°，由“角角边”依然可得△ABC≌△QGB，于是AC=QB 且AB=QG=BD.进而可证△BPD≌△QPG，得BP=QP，所以AC=QB=2BP.

深入分析可知：上述辅助线的作法虽然描述不尽相同，但本质就是在射线BP的右侧构造一个与△ABC全等的△QGB，从而把线段间的两倍关系转化为另两条线段间的相等关系.理所当然，也可在射线BP的左侧构造一个与△ABC全等的△BDQ加以证明.

证法4：如图3，过点D作DQ∥BG，交BP的延长线于点Q，思路同样为证明AC =BQ =2BP，即证明△ABC≌△DBQ和△BPG≌△QPD.

图3

易知∠BQD=∠QBG=∠ACB，根据“角角边”可证△BDQ≌△ABC，得DQ=BC=BG且BQ=AC.再由△BPG≌△QPD得BP=QP，问题迎刃而解.

上面证明都是从“倍长”出发的，当然也可从“截半”入手，打开思维通道.

证法5：如图4，在AC上截取AM=BP，连接BM，则根据“边角边”易知△AMB≌△BPD，得∠AMB= ∠BPD.由等角的补角相等得∠CMB=∠BPG.再依据“角角边”可证△BCM≌△GBP，得CM=BP=AM，所以AC=2BP.

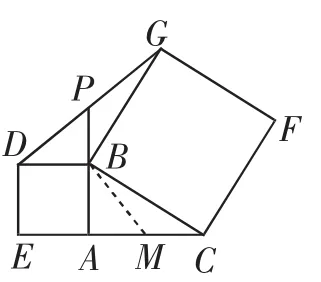
图4

当然图4中辅助线的作法也可表述为“在边CA上截取CM=BP”，证明时只需把证法5的过程稍作调整即可.

2.利用三角形中位线定理证明

证法6：由上面证明可知：事实上点P就是DG的中点. 又BP∥DE，故想到延长GB交DE的延长线于点N（如图5），构造以BP为中位线的△GDN.下面只需证明GB=BN 和DN=AC，即△ABC≌△DBN即可.

由∠ABC+∠ABN=∠DBN+∠ABN=90°，得∠ABC= ∠DBN.又AB=DB，∠BAC=∠BDN，则△ABC≌△DBN，故问题得证.

图5

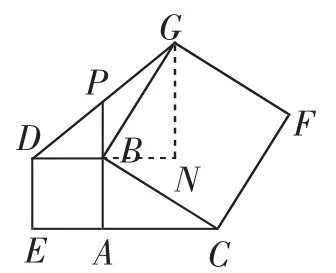
图6

证法7：当然也可过G作GN⊥DB交DB的延长线于N点，从另一方向构造以BP为中位线的Rt△DNG（如图6）.由“同角的余角相等”可得∠ABC=∠NBG，再根据“角角边”易证△ABC≌△NBG，得AC=NG、AB=NB=BD.而BP∥NG，所以NG=2BP，即AC=2BP.

三、证法反思

1.追根溯源巧定向

如何想到运用“线段中点定义”和“三角形的中位线定理”来证明本题的呢？

从知识转化角度略加分析可知：数学习题一般要运用所学过的知识加以解决，因此与线段二倍有关的知识源就是解决本题的思考方向和突破口.而回顾初中平面几何可知：与线段二倍关系有关的知识源除了上述两个知识点，还有“直角三角形斜边上的中线等于斜边的一半”和“直角三角形30°角所对的直角边等于斜边的一半”.考虑到本题缺少30°角且AC为直角边而非斜边，故解题方向宜定位在运用“线段中点定义”（证法1-5）和“三角形中位线定理”（证法6、7）两个知识源.

2.透过现象妙添线

利用线段中点定义证明AC=2BP无外乎有两个思考方向：一是倍长BP，二是截半AC.不过“倍长”和“截半”是指效果而已，具体操作可不拘一格.如本题若直接延长BP至点Q，使BQ=2BP，连接QG，但由于不知点P是否为DG的中点，得不到△BPD≌△QPG，给利用△ABC≌△QGB来证明BQ=CA制造了不小的障碍.相反换个角度思考，先构造BQ=AC再证明BQ=2BP，则可柳暗花明了！再如证法5中，若直接取AC的中点为M，也会给证明制造极大的障碍，但考虑到“截半”是为了确保三角形全等，不妨反其道而行之，直接构造全等三角形.

3.转换视角拓宽度

从上述七种证法中不难发现：转换视角是一题多解产生的本源.具体体现在：首先，在不同的知识间切换，明确一题多解之方向；其次，在不同对象间切换，寻求多解突破口（如“倍长”和“补短”）；还有同一辅助线在不同描述间切换，打开多解的切入点（如证法1-3）；最后在不同位置间切换，探求多解的发散点.当然，转换视角远非以上四点，只要平时注重探索与积累，一题多解在习题教学中必能绽放夺目之花、累结硕放之果.

总之，探求一题多解应基于知识转化策略之上，通过追根溯源，明确解题方向，调控受阻思维，寻求解决问题的基本途径.也就是说，首先明确解题目标（如本题为“证明线段二倍关系”），然后追溯初中阶段与此目标相关的知识源，最后结合条件确定解决本题的知识源，再转换视角，探求一题多解的自然生成.

参考文献：

1.曹青.一石激起千层浪万流归宗能力成——对充分挖掘题目教学功能的案例剖析与反思［J］.中学数学（下），2014（4）.

2.倪兴隆，袁庆明.对一道中考压轴题的解析与思考［J］.中学数学（下），2015（3）.

3.李艳娜.“兰利问题”求解的多种途径［J］.中学数学（下），2016（1）.