利用信息技术在数学实验中开展概念教学*

☉安徽省无为县刘渡中心学校　丁浩勇



利用信息技术在数学实验中开展概念教学*

☉安徽省无为县刘渡中心学校丁浩勇

数学是研究数量关系和空间形式的一门科学，数学概念就是人脑对这些数量关系和空间形式的本质特征的一种反映形式，它是构成数学法则、公式、定理等数学判断与推理的基础.正确理解数学概念是学生掌握数学基础知识和基本技能、发展逻辑推理能力和空间想象能力的前提.

由于数学概念是一种数学的思维形式，所以它具有一定的抽象性，这对抽象思维能力处于初级阶段的初中学生来说，掌握它具有一定的难度.但是，初中学生的直观思维尤为活跃，如果在概念教学时利用数学实验，把抽象的数学概念形象化，这对于化解教学难点、提高课堂教学效率将十分有益.事实上，早在上世纪中叶，著名的数学教育家波利亚就说过，数学有两个侧面，一方面它是欧几里得式的严谨科学，即是一门系统的演绎科学；但另一方面，创造过程中的数学，看起来却像一门实验性的归纳科学.波利亚告诉我们，数学不仅是一门系统的演绎科学，而且还是一门实验性极强的归纳科学，这充分说明数学实验是数学课堂教学中不可或缺的一部分.

所谓数学实验，就是人们以数学问题为载体，为获得某种数学理论，检验某个数学猜想或解决某类数学问题并运用一定的物质技术手段，在数学思维活动的参与下进行的一种数学实践活动.数学实验教学不同于传统的数学教学方式，它体现了皮亚杰的“建构主义”的思想和理念，强调的是以学生动手为主的数学学习方式，有利于培养学生的创新精神和发现问题的能力.因此，数学实验教学是一种新型、值得提倡的数学教学模式.

利用数学实验进行概念教学需要现代信息技术资源来支撑，概念教学过程中的测量验证、手工操作、动画演示等活动都离不开信息技术.充分利用信息技术开展数学实验教学，可以在引入概念、归纳概念、辨析概念、应用概念等教学活动中大显身手.

一、利用信息技术在数学实验中引入概念

由于数学概念研究的对象是现实世界的空间形式和数量关系，每个数学概念的产生都有它的现实背景，所以在进行概念教学时，可以精选现实生活或数学发展中的典型问题为背景，利用信息技术开展数学实验，直观呈现概念的产生背景，让学生感受数学概念的引入是自然而然、水到渠成的.

案例1：“概率”概念的引入.

实验构思：对于“概率”的概念，教材中只用文字叙述的方式直接向学生“传授”概念，学生不能明白“概率”的来龙去脉.其实概率是人们在研究现实世界的规律中产生的，如果利用信息技术再现研究过程，在实验的过程中让学生逐步消化“概率”，这样会有利于学生对“概率”意义的理解.为了节约时间和节省空间，可以利用Excel的随机函数RAND在课堂上做模拟投币实验来帮助学生理解“概率”.

实验过程：（1）如图1，在单元格A1中输入公式“=IF（RAND（）<0.5，“正面”，“反面”）”；

（2）在单元格B1中输入统计“正面”出现的次数公式“= COUNTIF（A∶A，“正面”）”；

图1

（3）在单元格B2中输入统计“反面”出现的次数公式“=COUNTIF（A∶A，“反面”）”；

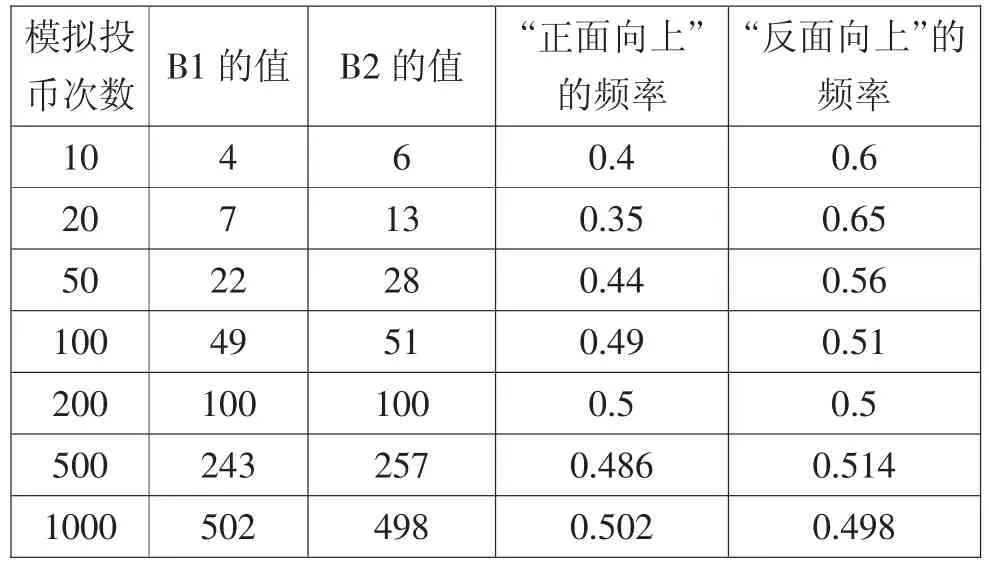
（4）按住单元格A1右下角的实心十字，向下拖动复制单元格，使A列中单元格包含与A1中公式相同的单元格总数分别是10、20、50、100、200、500、1000.重复模拟投硬币实验，分别记录每次拖动复制后单元格B1、B2中的数值，并完成下面的表格.

模拟投币次数10 B1的值4 B2的值6“正面向上”的频率0.4“反面向上”的频率0.6 20　 7　13　0.35　0.65 50　 22　28　0.44　0.56 100　 49　51　0.49　0.51 200　 100　 100　0.5　0.5 500　 243　 257　0.486　0.514 1000　 502　 498　0.502　0.498

问题1：观察实验结果，随着投币次数的增大，得到“正面向上”的频率与“反面向上”的频率有何种变化趋势？

问题2：根据实验结果预测投币试验中仅有的两种结果“正面向上”和“反面向上”出现的可能性大小分别是多少.

问题3：如何定义一个随机事件A发生可能性大小的数呢？

［实验评析］概率的研究对象是现实世界，因此，从学生的实际生活入手研究概率是最佳选择.由于受时间和空间的限制，课堂上再现实际研究过程不够现实.教学经验表明，组织一次实体投币实验，投币100次左右就要花费三十分钟时间，而利用信息技术模拟投币实验，几千次甚至上万次实验在几分钟之内就能完成.

本例通过随机函数RAND模拟投币试验，让学生亲自动手获得数据，从数据中寻找规律.问题1引导学生发现随着抛掷次数的增加，“正面向上”和“反面向上”出现的频率呈现一定的稳定性；问题2把随机事件发生的频率与随机事件出现的可能性大小紧密地联系起来；问题3通过设问的方式巧妙地引出概率的定义.这样让学生在实验的过程中主动构建概念，不但有利于调动学生学习概率知识的积极性，更有利于学生对概率意义的理解.

二、利用信息技术在数学实验中归纳概念

数学概念是从具体、形象的事物中抽象概括出来的，数学实验可以给学生创设具体的客观情境.如果利用信息技术开展数学实验再现概念的形成过程，将会有利于学生对概念的掌握.

案例2：“反比例函数的图像”概念的归纳.

实验构思：由于反比例函数的图像分置在两个象限，且两部分互不相连，这与学生前面学过的一次函数（包括正比例函数）、二次函数等连续的函数图像之间存在着一定的差异，导致学生根据已有知识和经验来理解反比例函数的图像有一定的困难.为了便于学生理解“双曲线”，可以利用“几何画板”软件创设一个面积不变的长方形模型，改变其形状，通过实验操作追踪其顶点位置形成轨迹，得出图像.

实验过程：（1）如图2，画一个长方形OABC，固定其面积等于18cm2；

（2）以O为原点，线段OA所在的直线为x轴，线段OC所在的直线为y轴，建立平面直角坐标系；

（3）拖动点B，并追踪点B的轨迹.

问题1：设图2中长方形的长OA为xcm，宽OB为ycm，那么y与x是怎样的函数关系？

问题2：图2中点B的坐标是什么？点B的运动轨迹是反比例函数图像的全部吗？

问题3：对于反比例函数的图像，你能根据对称性得出它的另一半吗？

［实验评析］利用几何画板软件的追踪轨迹功能，将反比例函数的图像通过实验呈现出来，将抽象的知识形象化，学生通过观察面积为定值的长方形的顶点移动生成的轨迹，在实验的过程中生成反比例函数的图像.

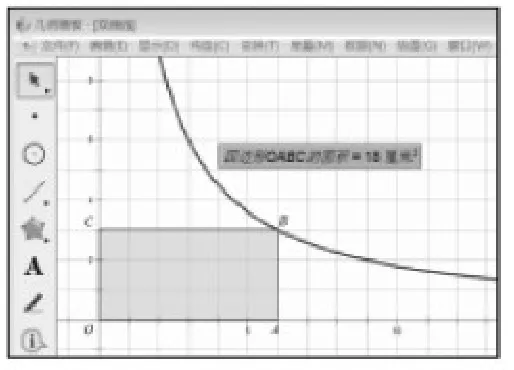
图2

问题1让学生明白长方形的宽y是长方形的长x的反比例函数；问题2指明B点的运动轨迹是反比例函数y=的图像的一部分；问题3进一步引导学生得出反比例函数y=的图像的另一部分.这样，先通过实验的直观呈现，突出“反比例函数的图像”的概念的生成过程，再通过解决层层推进的三个相关问题，活跃了学生的思维，符合学生的认知规律，有利于学生对“双曲线”概念的获取和归纳.

三、利用信息技术在数学实验中辨析概念

辨析概念是掌握概念过程中的一个重要环节，对概念进行辨析，可以突出概念的特有属性，澄清对概念的模糊认识，排除类似概念的干扰，肃清概念认识的误区.

辨析概念，可以把新概念置于同类概念之中，从形式上作比较，从本质上来区分.比如圆与圆的位置关系中的“内切”与“外切”、“相交”与“相离”、“内含”与“内切”、“外离”与“外切”等，虽然它们的定义只有一字之差，但是它们的本质却大相径庭.

案例3：辨析“圆与圆的位置关系”.

实验构思：利用几何画板软件制作动画直观演示圆和圆的5种位置关系，并同步显示两圆圆心距的大小，通过对实验现象的观察，让学生从形式上（两圆位置关系的图形呈现）和本质上（圆心距与两圆半径之间的数量关系）加以区分和辨析“圆与圆的位置关系”概念.

实验过程：（1）如图3，绘制相外离的⊙O1和⊙O2，度量并显示⊙O1和⊙O2的半径R、r（R＞r）的长度；

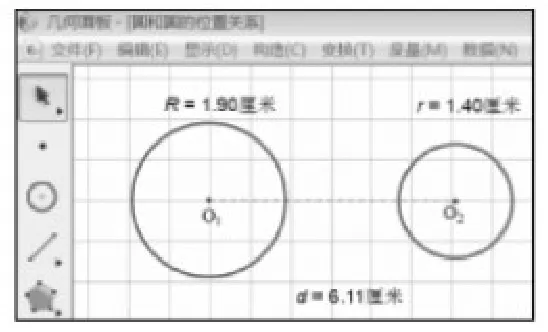
图3

（2）让⊙O2沿直线O1O2方向往⊙O1处慢慢平移，同步显示两圆的圆心距d的长度；

（3）当⊙O2运动到不同位置后形成新的位置关系时，暂停平移⊙O2，观察并记录两圆的圆心距d的长度后再继续平移⊙O2，如此反复，直到5种位置关系全部出现后停止平移⊙O2.

根据观察测量数据，填写表格.（填充完整的表格如下所示）

位置关系　圆心距与两圆的半径之间的关系外离　d＞R+r外切　d=R+r相交　R-r＜d＜R+r内切　d=R-r内含　d＜R-r

［实验评析］案例3利用信息技术工具，让学生在图形动态变化过程中发现圆和圆的5种位置.通过圆和圆的动态演示实验，学生既能从外显的形式上直观感知圆和圆的不同位置关系，从感观上对不同位置关系加以区分，又能让学生发现两圆具有不同位置关系时，它们的半径、圆心距之间的数量关系，从本质上加以区分外离、外切、相交、内切、内含的概念.

四、利用信息技术在数学实验中应用概念

概念的巩固应用是学习概念的归宿，学习概念的最终目的是为了能够灵活应用概念解决具体问题.反过来，通过概念的综合应用，又能把本概念与相关概念紧密地联系起来，将概念纳入概念系统，从而可以更清楚地认识概念的本质属性.

方程、不等式、函数之间存在着千丝万缕的联系，巧妙地构造函数，利用信息技术绘制函数的图像，在数学实验中得出关键点的坐标，可以有效地解决方程和不等式问题.这样设计教学，不但能提高学生的解题效率，而且便于学生更加“精致”地理解方程、不等式、函数的概念.

案例4：比较x2+2x与4x的大小.

实验构思：构造二次函数y=（x2+2x）-4x，即y=x2-2x，利用几何画板软件画出它的图像，显示图像与x轴的交点坐标.由图像验证y的正负性，得出x的取值范围，从而推出x2+2x与4x的大小.

实验过程：（1）如图4，画出二次函数y= x2-2x的图像；

（2）显示图像与x轴的交点坐标.

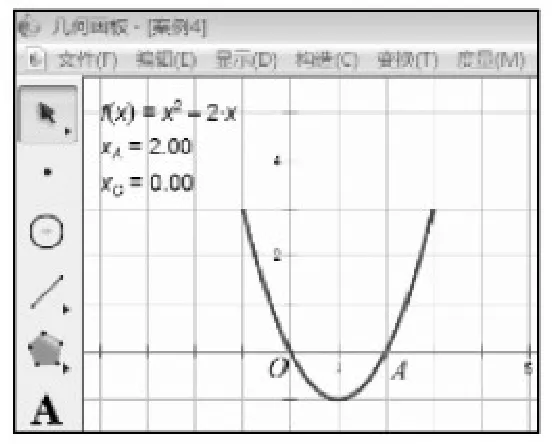
图4

问题1：观察图像，当自变量x取何值时，函数值y大于0？当自变量x取何值时，函数值y小于0？当自变量x取何值时，函数值y等于0？

问题2：当函数值y大于0时，x2+2x与4x的大小关系如何？当函数值y小于0时，x2+2x与4x哪一个大？当函数值y等于0时呢？

［实验评析］我国著名数学家华罗庚说过，数缺形时少直观，形少数时难入微；数形结合百般好，隔离分家万事休.数与形是数学研究的两个主要对象，在一定的条件下，它们之间可以相互转化，相互渗透.

案例4把不等式问题与方程问题巧妙地转化为函数图像问题来解决，通过作差法构造一个二次函数，然后利用信息技术画出这个函数的图像并显示出它与横轴的交点坐标，这样从图像上就可以判断出函数值的正负性与自变量的取值关系.问题1引导学生由图像看x取不同的值时，y的符号的正负性；问题2引导学生从函数值的正负性得出x2+2x与4x的大小关系.

参考文献：

1.朱林.数学实验活动课在教学中有效运用的策略［J］.中学数学（下），2015（12）.

2.路亚飞，葛丽雅，朱哲.活用信息技术强化初中几何概念教学［J］.中学数学（下），2015（8）.

3.丁浩勇.函数及其图像［J］.中学数学教学参考（中），2011（4）.

*基金项目：安徽省教育信息技术研究“十二五”规划立项课题——现代教育技术环境下的数学实验教学研究（AH2015056）.