Charged Noncommutative Wormhole Solutions via Power-Law f(T)Models
2016-05-10ShamailaRaniAbdulJawadandBilalAmin
Shamaila Rani, Abdul Jawad, and M.Bilal Amin
Department of Mathematics,COMSATS Institute of Information Technology,Lahore-54000,Pakistan
1 Introduction
Wormhole can be regarded as a tunnel or bridge from,which any object(or observer)may traverse easily.In other words,a wormhole is a hypothetical path that connects two different widely distant regions of the universe providing a kind of short-cut through spacetime. Although,there is no observational evidence for wormholes,they are known to be valid solutions under the general theory of relativity(GR).The Austrian physicist Flamm[1]while looking over Kerl Schwarzschild’s solution to Einstein’s field equation,realized first time this hypothetical connection.Later,it was further explored by Einstein along with Rosan[2]to construct Einstein–Rosan bridge(also known as Lorentzian wormhole or a Schwarzchild wormhole).However,Wheeler and Fuller predicted that they would collapse instantly if even the tiniest amount of matter(even a single photon)attempted to pass through them.
Thorne and Morris[3]demonstrated the possibility of transversable wormholes in GR.Wormholes that could be crossed in both directions known as traversable wormholes.A fundamental property of these solutions is the flaring out condition related to throat entails the violation of null energy condition(NEC)through the Einstein field equations.This violation is the necessary tool to establish wormhole solutions that allow two-way travel.In GR,wormhole spacetimes are supported by “exotic matter”,which involves a stress-energy tensor,i.e.,TµνKµKν<0 violating NEC(normal matter satisfies these conditions).The presence of unavoidable amount of exotic matter around the throat of wormholes and their mechanical stability are burning issues in Traversable wormholes.The problem of minimizing the usage of exotic matter for the physically viability of wormhole has received a considerable attention.For instance,it was shown that it is possible to reduce exotic matter around the wormhole throat,with suitable choice of wormhole geometry.
Modifications of GR are as much old as the theory itself.Most of modifications formed by introducing additional geometrical degree of freedom into the theory.The simplest extension of this theory isf(R)theory where Ricci scalarRrepresents curvature.The teleparallel gravity is an alternative geometrical formulation of GR.In GR,the gravitational interaction is geometrize by curvature whereas teleparallel gravity acts like a force assigns gravitation to torsion.From this point of view,curvature and torsion are simply alternative way of representation of same gravitational field.The attention is known attached to the torsion scalerT,which plays an important role in constructing the action of teleparallel theory.Hence a generalization of the teleparallel theory must contain higher order terms inT,which is named asf(T)theory,wherefis a di ff erentiable function of torsion scalarT.[4−19]
Jamilet al.[20]studied different exact solutions of static wormholes inf(R)gravity by taking noncommutative geometry.They considered power law model as well as particular form of shape function to construct these solutions.Rahamanet al.[21]derived the wormholes solutions for Lorentzian distribution in two different schemes firstly considered viable function and secondly assumed particular form of two shape functions and discussed all solu-tions graphically.Jawad and Rani[22]studied non commutative wormhole solutions in extended teleparallel gravity with the inclusion of noncommutative geometry under Lorentzian distribution for non diagonal tetrad.They explored solutions by taking power-lawf(T)and shape function models and discussed the stability(equilibrium conditions)of solutions for these models.Sharif and Rani[23]investigated charged wormhole solutions inf(T)gravity with noncommutative background by considering electrostatic field developed by a point charge.They used Gaussian distribution and effective energy-momentum tensor for diagonal and non-diagonal tetrad to develop field equations and compared with GR.They found that physical acceptable solution obtained for charge noncommutative wormhole solutions inf(T)gravity and exotic matter gives wormhole solutions in teleparallel case.
In this paper,we discuss charged NCL wormhole solutions for power lawf(T)models.We check the equilibrium condition for these solutions.The format of the paper is as follows.In Sec.2,we provide the wormhole geometry,its characteristics and flare out conditions.The energy conditions are also discussed.Section 3 is devoted for description of extended teleparallel gravity,non-diagonal tetrad and some discussion on electrostatic field.Section 4 contains the field equations for wormhole solutions inf(T)background taking NCL distribution.In Sec.5,we discuss wormhole solutions for teleparallel case and three power lawf(T)models.In the next section,we examine the equilibrium condition for all the solutions.The last section summarizes the results.
2 Wormhole Geometry
The static spherically symmetric wormhole spacetime is given by the line element[24]

At large distancesthe spacetime required to satisfy the condition of asymptotically flatness,i.e.,The flaring out condition must be satisfied to have the proper shape for a wormhole,which is carried through the ratio of the shape function to the radial coordinate at throat must be 1,away from throat,this coordinate represents a non-monotonic behavior.If we denote the throat radius asr0,this condition impliesβ(r0)=r0whileβ′(r0)≤1.It is notice that like the schwarzschild wormhole,which depends on the mass of wormhole,the Morris-Thorn wormhole is not a particular wormhole solution.There exist various solutions for an arbitrarily large number of shape as well as redshift functions satisfying the above constrains.
In order to deduce a number of general results in different physical contexts,the energy conditions are applied.The energy conditions come from the geometrical relationship of Raychaudhuri equation with attractive gravity.[26]Raychaudhuri equation givesfor timelike geodesics andfor null vector.If we replace Ricci tensor by the energy-momentum tensorTαβin these relations,we have energy conditions.We obtain the following forms of the energy conditions,when we assume a local frame of matter,which includesρandpas energy density and pressure
It is noted that an ordinary energy-momentum tensor satisfies the NEC.The matter distribution of the energy-momentum tensor at the wormhole throat must be negative,in order to prevent shrinking of the throat and to make it traversable.More precisely,the sum of the energy density and the pressure of matter is negative,representing a violation of the NEC and such matter is known as “exotic”.In order to support the wormhole solution,it is necessary to minimize the amount of exotic matter.The modified theories of gravity provides an effective energy-momentum tensor that violate NEC.The NEC is important in a sense that the violation of NEC leads to violate of the remaining energy conditions.Instead ofTαβ,the effective energymomentum tensoryields the energy conditions.By introducing the effective energy densityρeffand effective pressurepeffin the above mentioned inequalities,we get energy conditions.
3 Extended Teleparallel Gravity
The torsion scalarTis defined in the following form:

Here the torsion tensor is given as below:

it is antisymmetric in its lower indices,i.e.,is the superpotential tensor defined as:
It inherits anti symmetric property in its upper indices as well.Also contorsion tensoris as follows.
An orthonormal set of four-vector field(one timelike and three spacelike)called the tetrad field,uniquely specified the geometry of TP theory.The simplest tetrad(trivial tetrad)is of the formhereis kronecker delta.Because trivial tetrad provides zero torsion,therefore is of minor interest.The metric and tetrad fields are related as
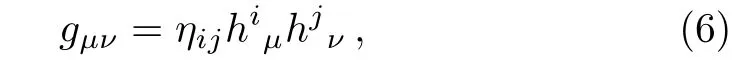
whereηij=diag(1,−1,−1,−1)is the Minkowski metric for the tanget space.Here the latin alphabets(i,j,k,...=0,1,2,3)are used for components of tangent space while the Greek alphabets(ν,µ,λ,...= 0,1,2,3)describe space-time components.The non-trivial tetrad fieldhjgives non-null torsion and construction of TP theory obtain,that spelled as
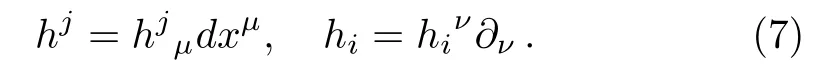
These are related by the following propertyWe follow covariant formalism,[27]in order to formulate a desirable form of the field equations that establishes the equivalent description(up to equation level).
After some algebraic manipulation and incorporating the last equations,it follows that:
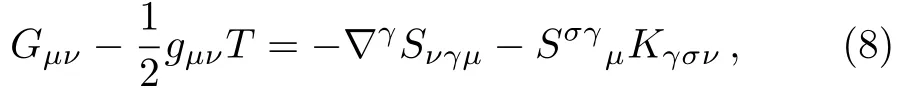
where,is the Einstien tensor.Finally,we get the following field equations forf(T)gravity:
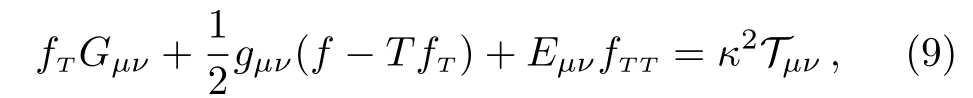
hereIn order to simplify and constrain the field equations the trace equation is used.The trace of last equation is
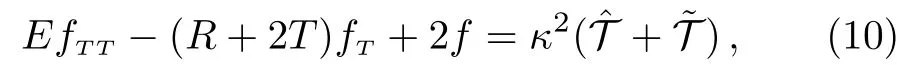
with.In effective energy-momentum tensor form,thef(T) field equation can be rewritten as
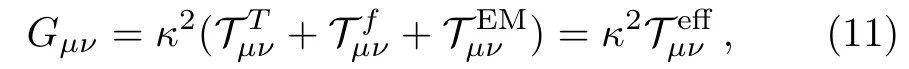
where the torsion contributionthrough trace equation is given by
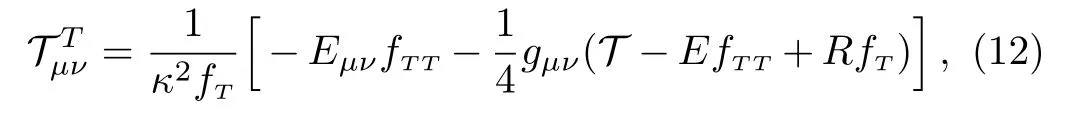
this equation takes the form(κ2=1)

whereJ(r)is
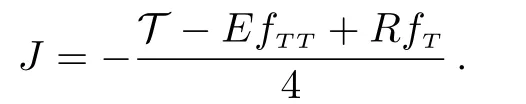
The termis related the matter fluid aswhilerepresents the electromagnetic energymomentum tensor as,where
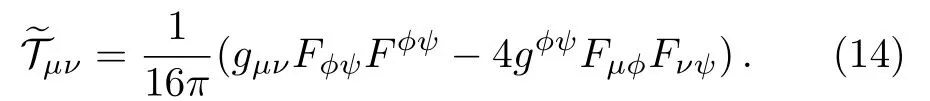
The termrepresents the Maxwell tensor withθαas four-potential.This tensor must satisfy the Maxwell field equations,i.e.whereJαis four-current andεois magnetic permeability.Here we assume that charge is spherically distributed,which is equivalent to point charge particle case.[28−29]Purely radial electrostatic field originate in the result of this point charge.In this case,the Maxwell tensor is of the form
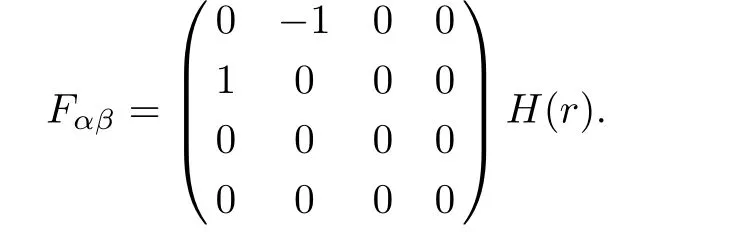
HereH(r)=q/r2is the electric field intensity corresponding to the point chargeq.
4 Field Equations for Wormhole Construction
The choice of tetrad field inf(T)gravity is very important in order to preserve modification.That is,working on spherical coordinates with diagonal tetrad give some unsuitable constraints on torsion scalar or on its modified form.[30]We have to face unwanted condition˙TfTT=0(orfTT=0)that yield torsion scalarTto be constant orf(T)=c1+c2Tsymbolizing TP theory.Therefore the diagonal tetrad is not a useful choice for spherical symmetry.As our objective to find out a realistic source for wormhole solutions inf(T)gravity,we consider the following nondiagonal tetrad for static spherically symmetric wormhole spacetime.
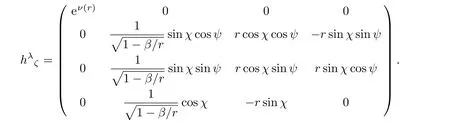
By using this non diagonal tetrad,the torsion scalar has the following form

Consider the anisotropic energy-momentum tensor as
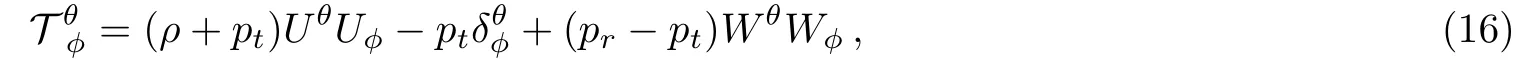
whereptandprare the transverse and radial components of pressure respectively.The unit spacelike vectorWθand four-vector of the fluidUθmust satisfyThe corresponding energy-momentum tensor is
Equation(11)gives the corresponding effective field equations

here prime shows derivative with respect tor.We consider effective energy density and pressure from Eqs.(17)and(18),the NEC yields
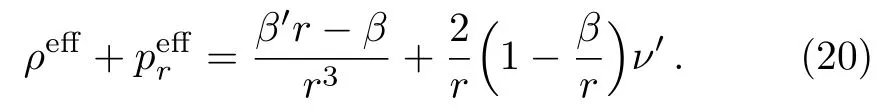
We havedue to flaring out condition,and it gives the violation of NEC withν′<0,i.e.,it shows that the effective energy-momentum tensor is responsible for violation of energy conditions to support wormhole geometry.Thus in this scenario condition may be on the usual matter to satisfy the energy conditions and provides some physically favorable solutions.
The magnitude of redshift function must be finite for traversable wormhole solutions. Takingν=0 in Eqs.(17)–(19),the field equations rewrite as
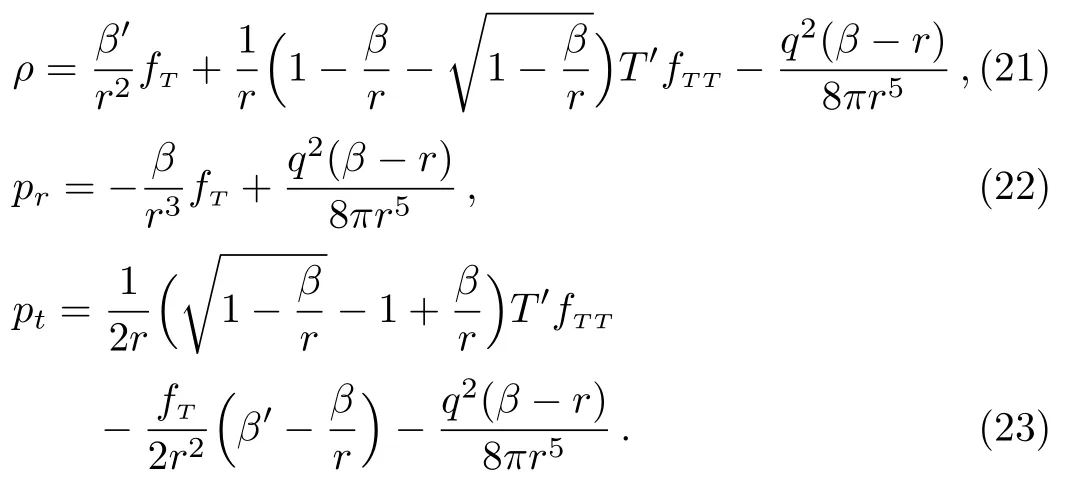
Torsion scalar becomes
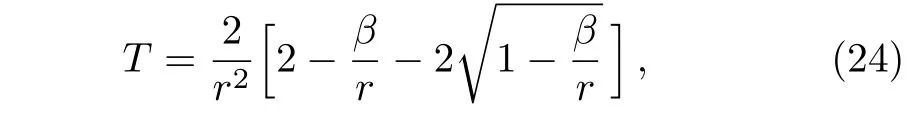
and it derivatives w.r.t(r)gives

Due to flaring out the condition we see Eq.(20),gives the violation of NEC.
5 Wormhole Solutions
The coordinate coherent state approach is widely used in order to formulate the noncommutative form of GR.Being the intrinsic characteristic of spacetime,noncommutative geometry plays an important role in several areas.By replacing the point-like structures with smeared objects in noncommutative geometry,we vanish the divergencies that appear in GR.The energy density of the particle-like static spherically symmetric gravitational source having massMtakes the following form[31]under Lorentzian distribution
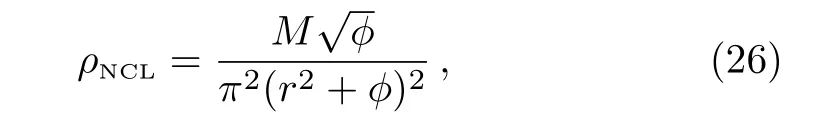
whereϕis the noncommutative parameter.The correspondence betweenρandρNCLgives the following differential equation
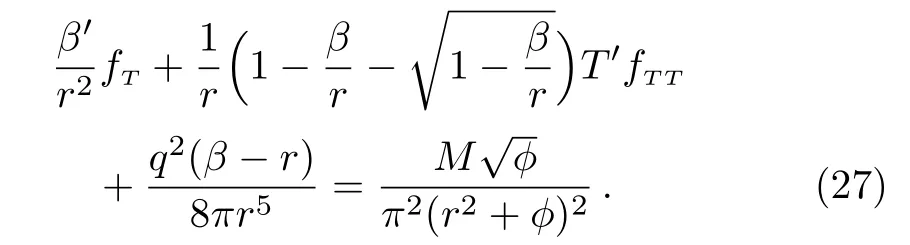
This equation contains two unknown functions such asβandf.Thus we choose one of these functions and carry out steps for the other one.We investigate the behavior of the energy conditions for specificf(T)power law models and discuss the NCL wormhole solutions inf(T)gravity for a non-diagonal tetrad.
We consider particular power lawf(T)model analog tof(R)model likef(R)=R+λRnto discuss the wormhole solutions.Thef(T)model is
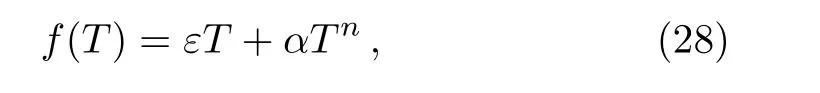
whereε,αandnare arbitrary constants.Due to its simple form,f(T)model has contributed as the most viable model and we may directly compare our results with GR.In the following,we discuss this power law model under different conditions.
Teleparallel Casef(T)=εT
Firstly,we discuss wormhole solutions for teleparallel gravity which is acquired by takingα=0 in model(28).It yields

Inserting the value offTandfTTin Eq.(27),it implies
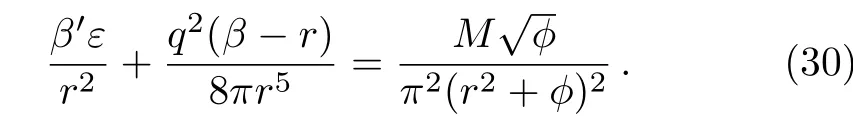
Here we neglectβq2like terms because these terms involve interaction between wormhole geometry and charge.Under higher or lower collective interaction terms,wormhole geometry may or may not affect by this negligence.However,for the sake of simplicity we ignore these terms and obtain the following differential equation

which yields the solution
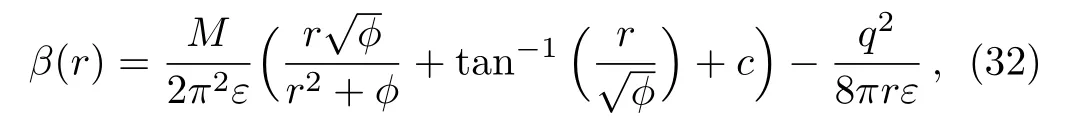
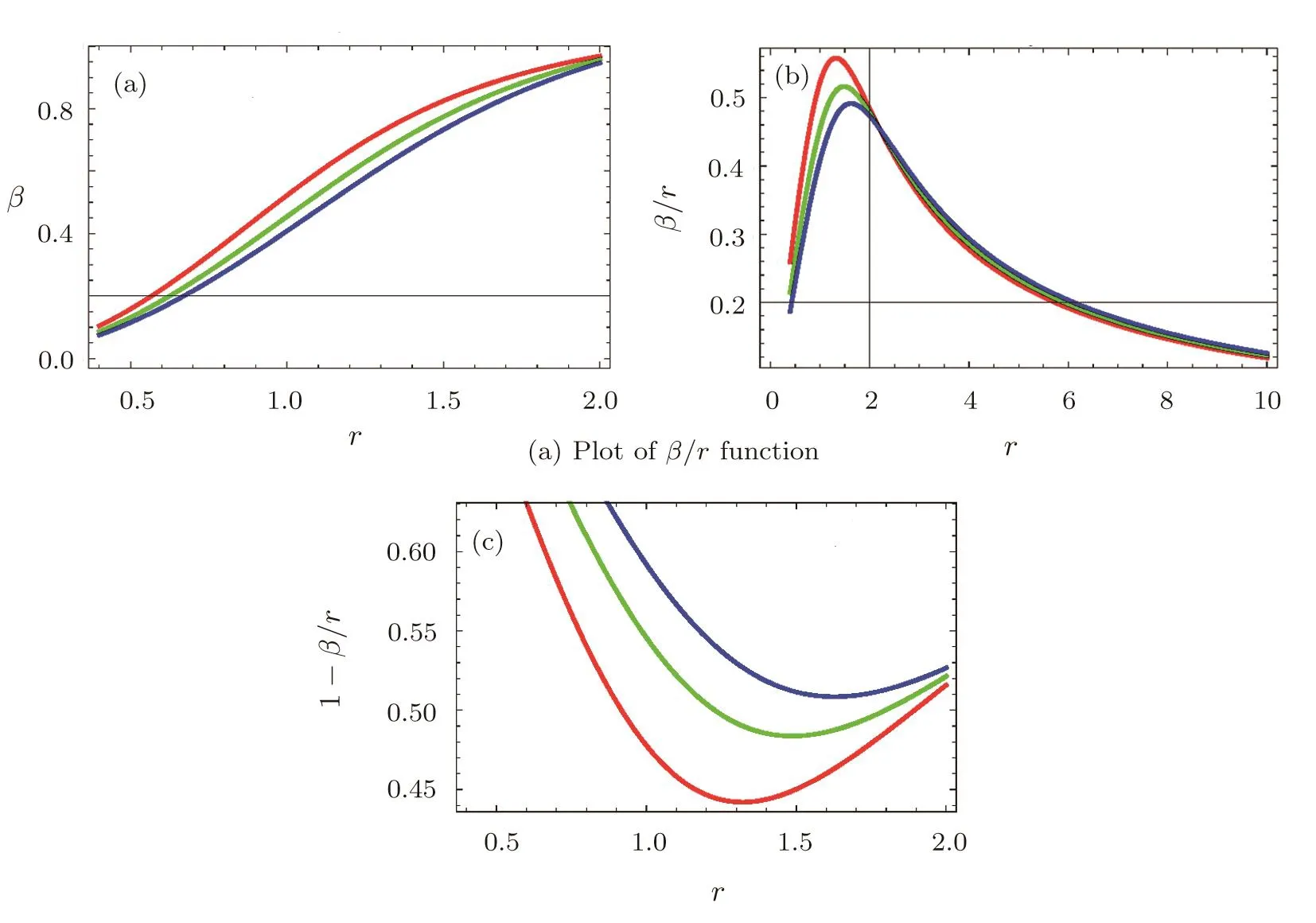
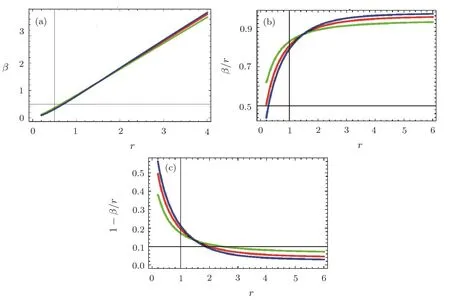
wherecis an arbitrary constant.To examine the wormhole geometry graphically,we choose arbitrary values of parameters to draw the shape function,such as,c=1,ϕ=3,M=3,q=0.1 andε=1.The behavior of the shape functionβ(r)appears increasing againstras shown in Fig.1(a).In Fig.1(b),the asymptomatically flatness condition is acquired asfor increasingr.The behavior of 1−β(r)/rrepresents increasing trajectory from negative to positive as shown in Fig.1(c).Therefore wormhole solution does not exist forr≤0.159 as 1−β(r)/ris negative for these values ofrwhile it exists for all values ofr>0.159.
Equations(17)–(19)take the form
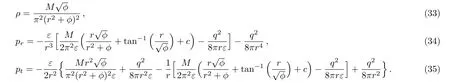
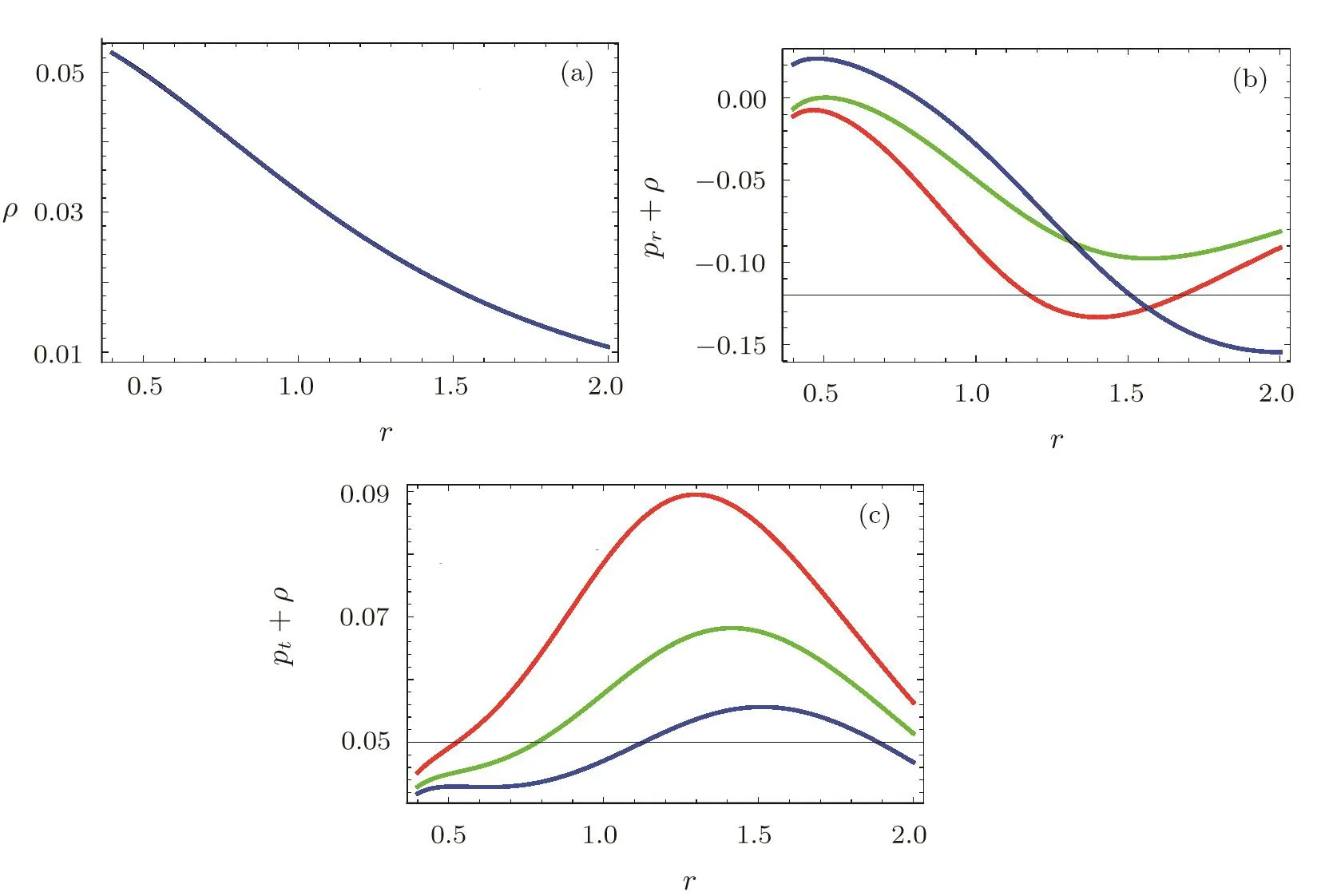
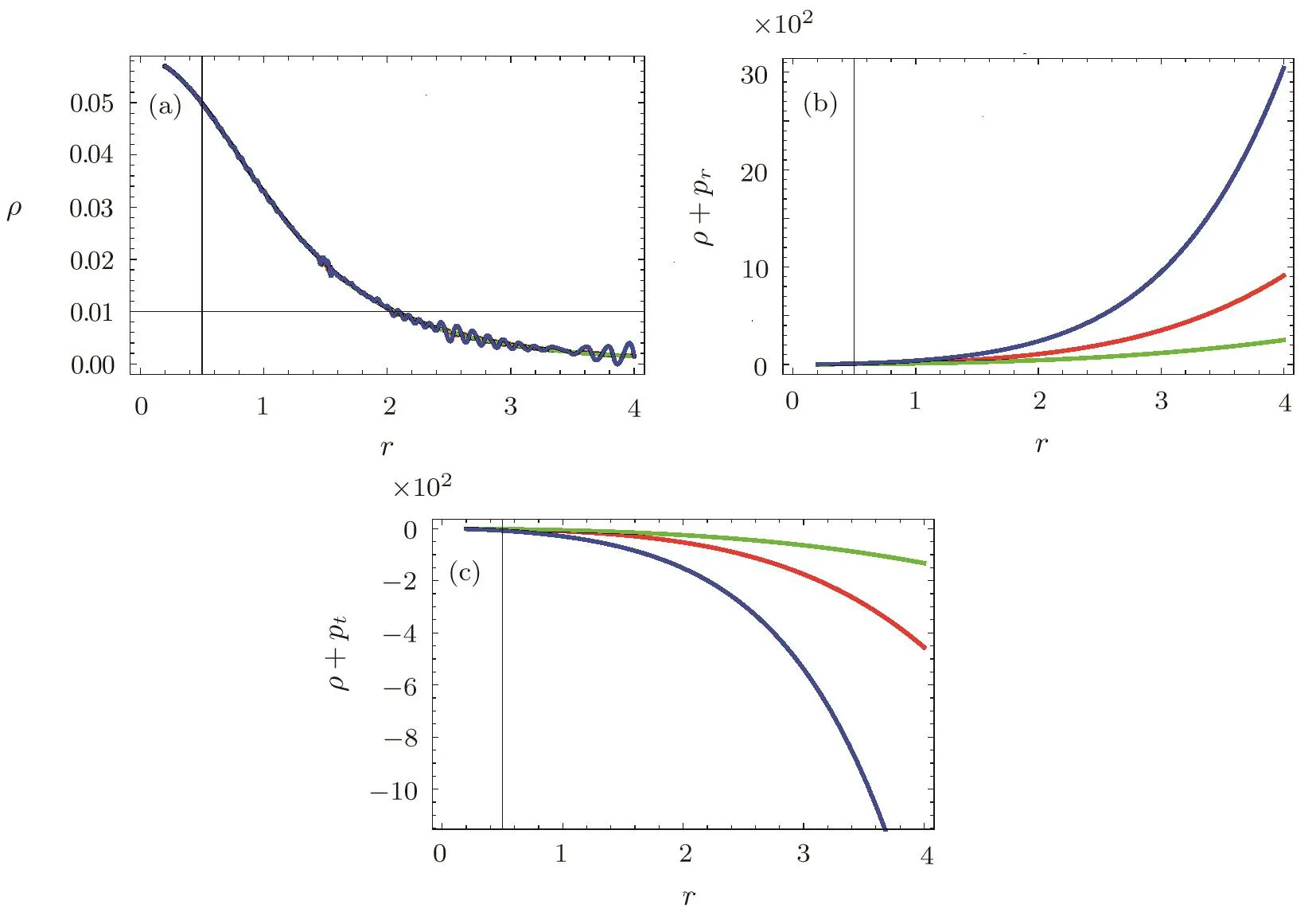
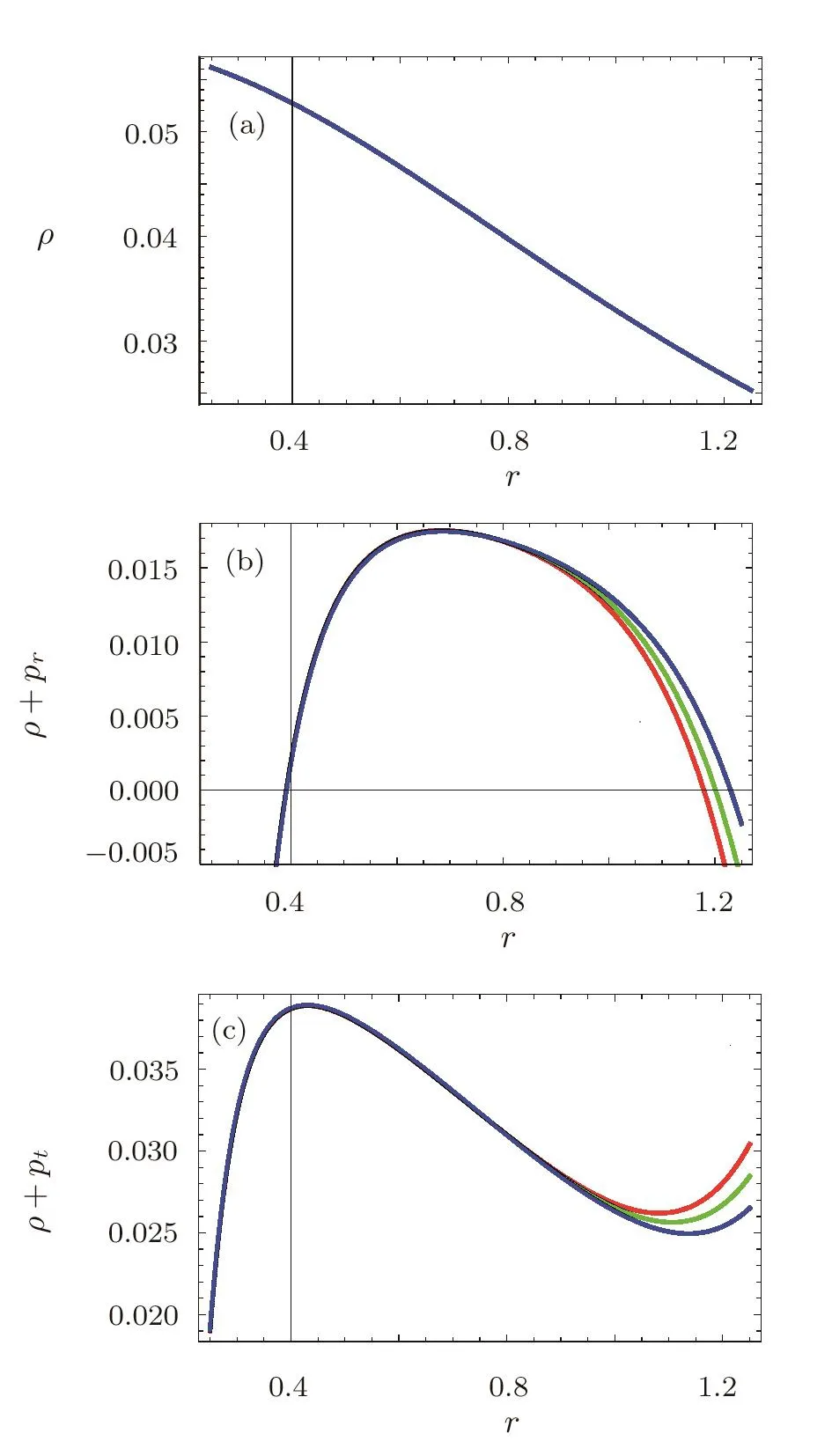
We plot WEC(ρ,ρ+prandρ+pt)versusrto observe the behavior of energy conditions for charge NCL wormhole solutions in teleparallel case,as shown in Fig.2.It can be seen that the energy densityρandρ+prpositively decreasing with the increasing value ofrwhileρ+ptsuffers negative values,which gives the violation of WEC.This implies that the charged NCL wormhole solution is supported by exotic matter for teleparallel case.

Fig.1 (Color online)Plots of shape function β(r)in teleparallel case:(a) β(r)versus r,(b) β(r)/r versus r and(c)1−β(r)/r versus r.
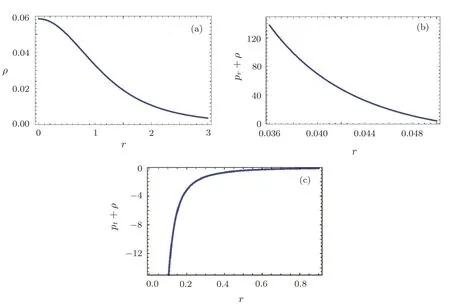
Fig.2 (Color online)Plots of WEC in teleparallel case:(a)ρ versus r,(b)ρ+prversus r,(c)ρ+ptversus r.
Model 1
We consider power-lawf(T)model in the following form
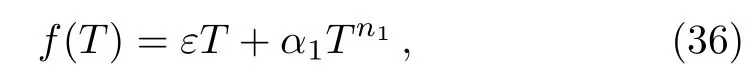
hereε,α1andn1are arbitrary constant.The first and second order derivatives of this function w.r.t torsion scalarTare given as
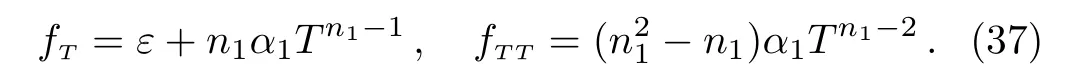
Inserting these values in Eq.(27),we get
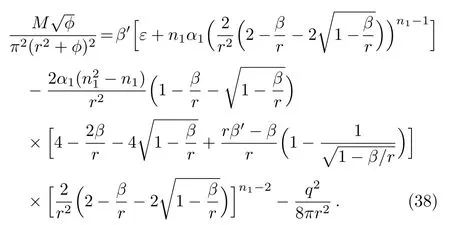
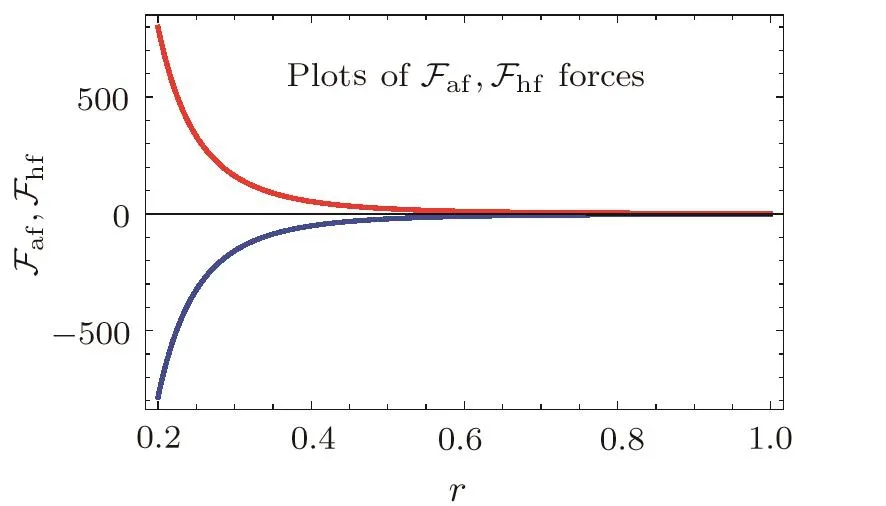
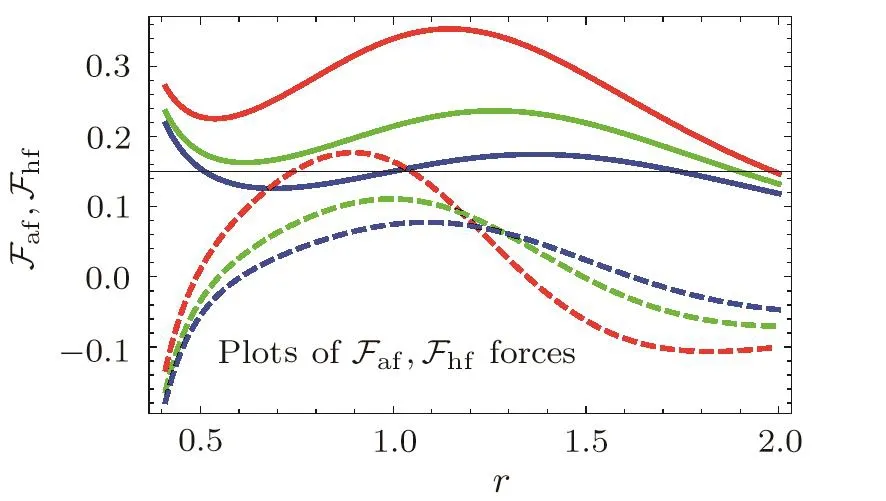
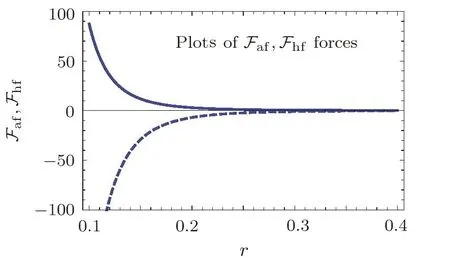
Taking same values of parameters as for teleparallel case along with three different values ofα1such asα1=−2,−3,−4 and settingf[2.2]=1,we plot shape function and flaring out condition through some numerically computations.The shape function represents increasing behavior versusras shown in Fig.3(a).The functionβ/rindicates asymptomatically flat behavior forexpressing through Fig.3(b).In Fig.3(c),the behavior ofversusris decreasing but remains positive for the values ofr.This implies that flaring out condition for wormhole geometry is obtained.Figures 4(a)–4(c)show the graphs of WEC expressions versusr.The trajectories of energy density as well asρ+ptrepresent positive behavior for all values ofαas describes by Figs.4(a)–4(c).However,ρ+prexpresses negative behavior for increasing value ofα1.This implies that there exists possibility of realistic wormhole solutions forα1=−4,r<0.9 as well as for forα1=−3,0.48 Model 2f(T)=α2Tn2 As a second model,we assumeε=0 and replaceαbyα2,nbyn2in Eq.(28)analogy tof(R)model likef(R)=λRn,which provides the generalization of GR.Thef(T)model is given as Here,α2represents a non-zero constant whileto avoid the teleparallel case.Inserting this model along with its derivatives in Eq.(27),it takes the form Fig.3 (Color online)Plots of shape function β(r)for model 1:red curve for α1= −2,green curve for α1= −3,blue curve for α1= −4,(a)β(r)versus r,(b)β(r)/r versus r and(c)versus r. Fig.4 (Color online)Plots of WEC for Model 1:red curve for α1= −2,green curve for α1= −3,blue curve for α1=−4,(a)ρ versus r,(b)ρ+prversus r,(c)ρ+ptversus r. We plot the shape functionβ(r)againstrby taking same values of some parameters while remaining are chosen asα2=3 along with some particular values ofn2liken2=−1.5,−2,−2.5 and set the initial value asf[1.5]=1.3 as shown in Figs.5(a),5(b),and 5(c).Under the values of parametern2,thef(T)model represents the torsion scalar as reciprocal term.The shape function shows positively increasing behavior while the evolution of 1−β/ragainstris decreasing.This decreasing behavior remains positive for all values ofn2andr,which represents the validity of flare out condition for wormhole geometry.However,the asymptomatically flat condition is not satis fied for thisf(T)model.In order to examine the behavior of energy conditions for charged NCL wormhole solutions inf(T)case,we plot WEC againstr,as shown in Figs.6(a)–6(c).This expresses thatρandρ+prkeep positive behavior whileρ+ptgives the negative trajectory.This depicts that WEC violates and no realistic wormhole solutions exists in this case. Fig.5(Color online)Plots of shape function β(r)for model 2:green curve for n2= −1.5,red curve for n2= −2,blue curve for n2= −2.5,(a)β(r)versus r,(b)β/r versus r and(c)1−β/r versus r. Fig.6 (Color online)Plots of WEC with non diagonal tetrad for model 2:green curve for n2=−1.5,red curve for n2= −2,blue curve for n2= −2.5,(a)ρ versus r,(b)ρ+prversus r,(c)ρ+ptversus r. Model 3 Here,we take model 3 by consideringε=0 and replacingα3,n3toα,nandin Eq.(28).The power-law model becomes Use this model in Eq.(27),we obtain the following equation Fig.7 (Color online)Plots of shape function β(r)for model 3:red curve for α3= −6,green curve for α3= −5,blue curve for α3= −4,(a)β(r)versus r,(b)β(r)/r versus r and(c)1−β(r)/r versus r. Fig.8(Color online)Plots of WEC with non diagonal tetrad for model 3:red curve for α3= −6,green curve for α3= −5,blue curve for α3= −4(a)ρ versus r,(b)ρ+prversus r,(c)ρ+ptversus r. Figure 7(a)shows the shape function trajectory with respect tortaking same values of parameters whilen3=3 andα3=−6,−5,−4 along with initial valuef[1.5]=1.This represents the increasing behavior of shape function for all values ofα3while does not fulfill the condition of flatness as shown in Fig.7(b).Figure 7(c)demonstrates the trajectory of 1−β/ragainstras decreasing with positive nature.This establishes the wormhole geometry for the charged NCL wormhole solutions inf(T)gravity background.The plots of energy condition for charged NCL wormhole solution corresponding tof(T)model 3 are shown by Figs.8(a)–8(c).We examine thatρrepresents positive behavior for all values of model parameterα3.The trajectories in plotρ+prshow negative behavior initially forr<0.4 and then turns towards positive panel.These trajectories remain positive for the range 0.4≤r<1.17 representing validity of energy condition for the componentρ+prand after this range,these again become negative for increasingr.Theρ+ptshows increasing/decreasing behavior but remains positive with increasing value ofrfor allα3.Therefore WEC satisfies for particular ranges and leads to the pliability of wormhole solutions supported by charge and effective energymomentum tensor. In order to check the stability of wormhole geometry with the help of equilibrium condition,we take the generalized Tolman–Oppenheimer–Volkov equation[32−33]for anisotropic mass distribution as for the metric ds2=diag(eµ(r),−eω(r),−r2,−r2sin2θ). The equilibrium con figuration for the wormhole solutions indicated by this equation is acquired through anisotropic force due to anisotropic matter distribution,gravitational and hydrostatic forces.Using Eq.(43),we can define these forces as follows For the equilibrium of wormhole solutions,it is required that Here the parameterµrepresents the gravitational redshift,which is considered as constant in underlying case,i.e.µ=2νthat leads toµ′=0.This yields the vanishing of gravitational force and equilibrium condition takes the formFaf+Fhf=0 corresponding to anisotropic and hydrostatic forces.For teleparallel caseFhfandFaftake the form These forces for models 1,2,3 are given by Fig.9(Color online)Plot of anisotropic force Faft(red)and hydrostatic force Fhft(blue)against r for teleparallel case. Fig.10 (Color online)Plot of anisotropic force Faf1(solid)and hydrostatic force Fhf1(dotted)against r for Model 1. We plot these equations to check the equilibrium of wormhole solutions obtained for teleparallel case andf(T)models are shown in Figs.8–12 respectively.In teleparallel case,we see that the behavior of anisotropic and hydrostatic forces is identical but in opposite direction,which results the equilibrium of the solution.For first powerlawf(T)model 1,we examine that these solutions do not satisfy equilibrium condition properly but we can say that these solutions are less stable.In the case off(T)model 2,Fig.11 expresses that the behavior of both forces(Faf2andFhf2)is same direction wise.Thus,these solutions are not stable for any value ofr.We observe that forcesFaf3andFhf3having same behavior but in opposite direction for higher values ofr,i.e.,balance each other for model 3.Thus,the solutions for this model are also stable. Fig.11 (Color online)Plot of anisotropic force Faf2(solid)and hydrostatic force Fhf2(dotted)against r for Model 2. Fig.12 (Color online)Plot of anisotropic force Faf3(solid)and hydrostatic force Fhf3(dotted)against r for Model 3. Wormhole physics has been an interesting subject for researchers due to its topological phenomenon.Wormholes are the hypothetical objects containing exotic matter that violates NEC.The first wormhole model given by Einstein-Rosen bridge[2]but this wormhole prevents observer to move freely from one universe to the other due to existence of event horizon.Later,Morris and Thorne[3]presented the first traversable wormhole solution of Einstien field equations,which does not contain event horizon and observer may pass freely in both regions of universe through tunnel(wormhole throat).There are some major issues in traversable wormholes such as presence of inevitable amount of exotic matter at the throat,and their stability etc.The main hurdle in its observational evidence is the violation of NEC,due to exotic matter is a hot issue in GR.The problem of minimizing the usage of exotic matter for the physically viability of wormhole has received a considerable attention.Therefore,it leads to explore a realistic model in favor of wormhole.In this paper,we have studied charged wormhole solutions inf(T)gravity by considering static spherically symmetric spacetime in NCL background. We have taken non-diagonal tetrad and developed thef(T) field equations in terms of effective energymomentum tensor and observed that,instead of exotic matter,this tensor provides the necessary support for construction of wormhole solutions.We have considered power-lawf(T)model under various conditions on its parameters and examined wormhole solutions.The graphical behavior of shape function,asymptomatically flatness condition, flaring out condition,WEC and equilibrium of these solutions are discussed.First of all,we have explored the charged NCL wormhole solution of teleparallel gravity and observed that these solutions supported by exotic matter only.The conditions for wormhole geometry on shape function are satisfied by each model.The WEC is satisfied for the models 1 and 3 in a particular range ofrin each case while violated in model 2.We conclude that under NCL background,the possibility of physically acceptable charged wormhole solutions exists,where the role of exotic matter plays by effective energy-momentum tensor. Also,by using generalized Tolman–Oppenheimer–Volkov equation,we have examined the equilibrium of these wormhole solutions.We have found that teleparallel charged NCL wormhole solutions are stable.For first power-lawf(T)model 1,we examine that these solutions do not satisfy equilibrium condition however these solutions are less stable.In the case off(T)model 2,the behavior of both forces(Faf2andFhf2)is same direction wise.Thus,these solutions are not stable for any value ofr.We observe that forcesFaf3andFhf3having same behavior but in opposite direction for higher values ofr,i.e.,balance each other for model 3.Thus,the solutions for this model are also stable.It is mentioned here that our results reduce to the uncharged case of wormhole solutions for non-diagonal tetrad in NCL background whenq=0.[22] References [1]L.Flamm,Phys.17(1916)448. [2]A.Einstein and N.Rosen,Phys.Rev.48(1935)73. [3]M.S.Morris and K.S.Thorne,Am.J.Phys.56(1983)395. [4]E.V.Linder,Phys.Rev.D81(2010)127301. [5]K.Bamba,C.Q.Geng,and C.C.Lee,arXiv:astroph/1008.4036. [6]K.Bamba,C.Q.Geng,C.C.Lee,and L.W.Luo,J.Cosmol.Astropart.Phys.1101(2011)021. [7]K.Bamba,et al.Phys.Rev.D85(2012)104036. [8]K.Bamba,S.Capozziello,S.Nojiri,and S.D.Odintsov,Astrophys.Space Sci.342(2012)155. [9]K.Bamba,S.Nojiri,and S.D.Odintsov,Phys.Lett.B731(2014)257. [10]M.Jamil,D.Momeni,and R.Myrzakulov,Eur.Phys.J.C72(2012)1959. [11]M.Jamil,D.Momeni,and R.Myrzakulov,Eur.Phys.J.C72(2012)2137. [12]M.Jamil,D.Momeni,and R.Myrzakulov,Eur.Phys.J.C73(2013)2267. [13]M.Sharif and S.Rani,Gen.Relativ.Gravit.45(2013)2389. [14]M.Sharif and S.Rani,Phys.Rev.D88(2013)123501. [15]A.Jawad and S.Rani,Eur.Phys.J.C75(2015)173. [16]A.Jawad and S.Rani,Eur.Phys.J.C75(2015)548. [17]A.Jawad,S.Rani,and S.Chattopadhyay,Astrophys.Space Sci.360(2015)37. [18]A.Jawad,S.Chattopadhyay,and S.Rani,Astrophys.Space Sci.361(2016)231. [19]M.Sharif and S.Rani,Mod.Phys.Lett.A28(2013)1350118. [20]M.Jamil,M.U.Farooq,and M.A.Rashid,Eur.Phys.J.C59(2009)907. [21]F.Rahaman,S.Islam,P.K.F.Kuh fittig,and S.Ray,Phys.Rev.D86(2012)106010. [22]A.Jawad and S.Rani,Eur.Phys.J.C75(2015)173. [23]M.Sharif and S.Rani,Eur.Phys.J.Plus129(2014)237. [24]M.Morris and K.Thorne,Am.J.Phys.56(1988)395. [25]M.Visser,S.Kar,and N.Dadhuch,Phys.Rev.Lett.90(2003)201102. [26]S.Carroll,Spacetime and Geometry:An Introduction to General Relativity,Addison Wesley,New York(2004). [27]B.Li,T.P.Sotiriou,and J.D.Barrow,Phys.Rev.D83(2011)064035;ibid.83(2011)104017;T.P.Sotiriou,B.Li,and J.D.Barrow,Phys.Rev.D83(2011)104030;D.Liu and M.J.Reboucas,Phys.Rev.D86(2011)083515. [28]S.W.Kim and H.Lee,Phys.Rev.D63(2001)064014. [29]A.Aghamohammadi,et al.,Int.J.Theor.Phys.49(2010)709. [30]C.G.B¨ohmer,A.Mussa,and N.Tamanini,Class.Quantum Grav.86(2012)245020. [31]P.Nicolini,A.Smailagic,and E.Spalluci,Phys.Lett.B632(2006)547. [32]F.Rehaman,P.K.F.Kuh fittig,S.Ray,and N.Islamd,Eur.Phys.J.C74(2014)2750. [33]P.K.F.Kuh fittig,Eur.Phys.J.C74(2014)2818.
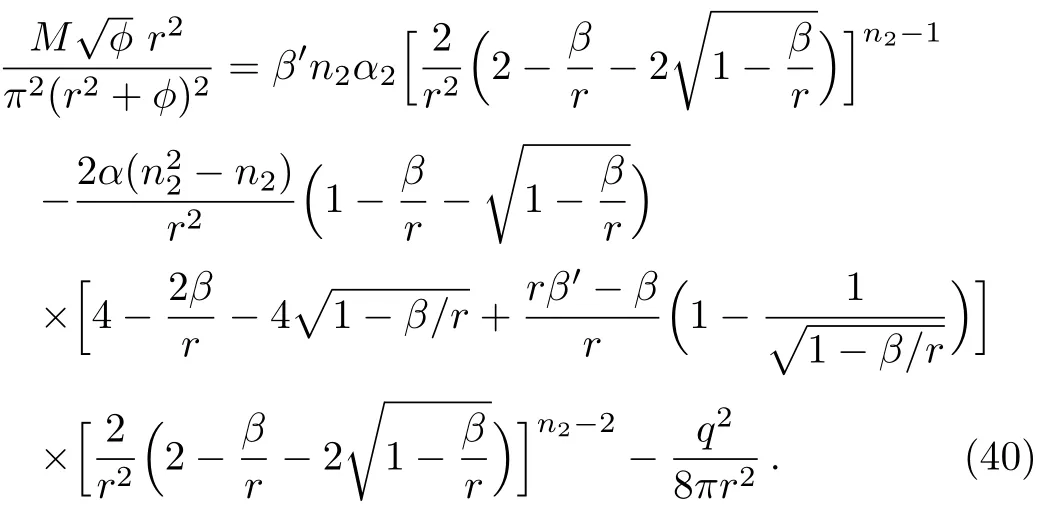
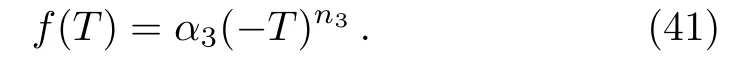
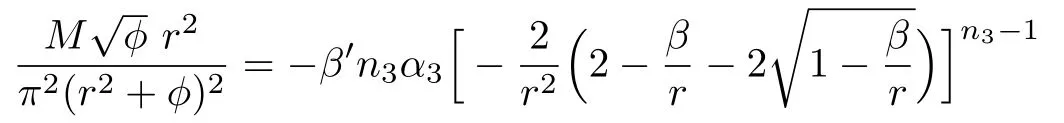


6 Equilibrium Condition for Wormhole Solutions
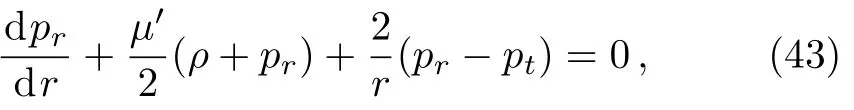

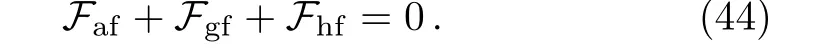
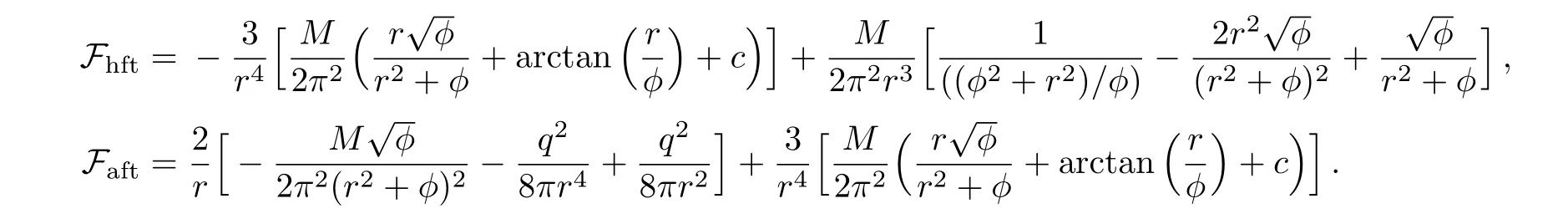

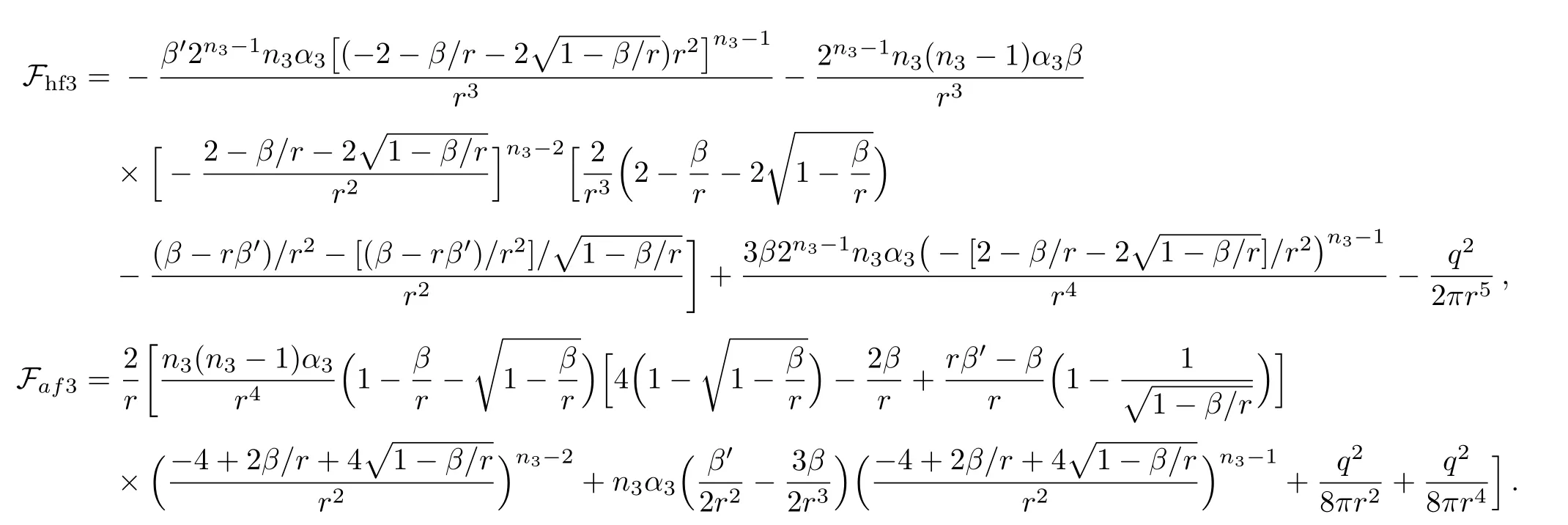

7 Summery and Concluding Remarks
杂志排行
Communications in Theoretical Physics的其它文章
- E ff ect of Mis fit Strain on Pyroelectric Properties of(111)Oriented Pb(Zr1−xTix)O3 Thin Films∗
- In fluence of Defects and Crystallographic Orientation on Mechanical Behavior of Nanocrystalline Aluminium∗
- Critical Behavior of Spatial Evolutionary Game with Altruistic to Spiteful Preferences on Two-Dimensional Lattices∗
- First-Principles Study of Structural,Magnetic,Electronic and Elastic Properties of PuC2∗
- Study of Friction between Liquid Crystals and Crystalline Surfaces by Molecular Dynamic Simulations∗
- Relativistic Correction on Neutrino Emission from Neutron Stars in Various Parameter Sets∗
