Monogamy Relations for Squared Entanglement Negativity∗

Feng Liu(刘锋)

College of Mathematic and Information Science,Shandong Institute of Business and Technology,Yantai 264005,China State Key Laboratory of Networking and Switching Technology,Beijing University of Posts and Telecommunications,Beijing 100876,China

1 Introduction

Measures of entanglement have played a key role in the quantum information processing.Given a wave function of two subsystemsAandB,the von-Neumann entropy of the reduced density matrixρAis used to quantify the amount of bipartite entanglement.[1]However,the calculation of the entanglement for mixed states is generally difficult due to the convex roof extension.To fill the important gap in the study of mixed-state entanglement,Vidal and Werner[2]presented the entanglement negativitywhere the symbolTAmeans partial transpose with respect to the subsystemA,and the trace normThe entanglement monotone can be computed effectively for mixed-state entanglement,and it can also be used as a tool for understanding multipartite entanglement.In order for any maximally entangled state in 2⊗2 systems to have the negativity 1,it can be reexpressed as[3]

with only a change of the constant factor 2.

different from classical correlations,entanglement cannot be freely shared among multipartite states.[4]The monogamy relation is a fundamental property of multipartite entanglement states,and has been a research highlight.[5−11]For allm-qubit statesρA1A2···Am,Ou and Fan[3]analytically proved that the squared entanglement negativity obeys the following monogamy relation

whereA1is the focus qubit.Recently,He and Vidal[12]numerically verified the validity of Eq.(2)for randomly hundreds of states in(n=2,3,and 4)systems,and then made a conjecture that the monogamy inequality(2)should be valid for arbitrary tripartite systems(i.e.,the He–Vidal conjecture).On the other hand,for four-qubit states,the difference between left and righthand sides of the conventional Co ff man–Kundu–Wootters inequality[13]just gives a rough indicator of all the multipartite entanglement score not distributed in pairwise form.To extend and sharpen these existing monogamy inequalities,Regulaet al.[14]defined a strong monogamy relation for tangles

where the index vectorspans all the ordered subsets of the index set{2,...,m}with(n−1)distinct elements.They verified it on arbitrary four-qubit pure states.Further,they conjectured that other entanglement measures(e.g.,the entanglement negativity),which satisfy conventional monogamy relations,would also obey the strong monogamy inequality for arbitrary four-qubit states(i.e.,the squared-negativity-based Regula–Martino–Lee–Adesso-class conjecture).

In this paper,we present two counterexamples for the squared entanglement negativity,where the first one disproves the He–Vidal monogamy conjecture on some threequtrit systems,and the second one negates the Regula–Martino–Lee–Adesso-class strong monogamy conjecture on some four-qubit states.Moreover,we apply the strong monogamy score to a practical dynamical procedure of a composite system,[15]which is composed of two entangled cavity photons being affected by the dissipation of two individualL-mode reservoirs.

2 A Counterexample for the He–Vidal Conjecture

He and Vidal[12]conjectured that the squared entanglement negativity is always monogamous for arbitrary tripartite systems.They numerically verified the conjecture and claimed that there does not exist any counterexamples violating of it.

In this section,we will show that the generalized Aharonov state

wherewill violate the He–Vidal monogamy conjecture in 3⊗3⊗3 systems.

For the standard Aharonov state,It violates the original Co ff man–Kundu–Wootters inequality for the squared concurrenceC2,[16]sinceAccording to Eq.(1),we havethen the squared entanglement negativity satisfies the monogamy relation(2).However,the result cannot be always true for the general Aharonov state.

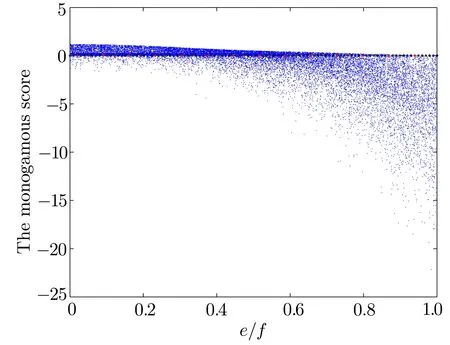
Fig.1 (Color online)The three-qutrit states in Eq.(4)violate the monogamous relation for the larger e or f,where the monogamy score isin Eq.(4).When the highest dimension of the focus particle becomes bigger,the violation degree of the monogamous relation is stronger.

In three-qutrit systems,we have randomly generated 104generalized Aharonov states and computed both sides of Eq.(2).The monogamy score

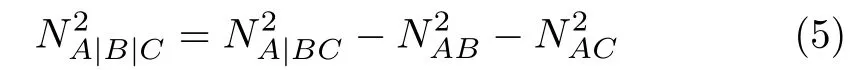
as a function ofeis shown in Fig.1.Our numerical results are diminishingly consistent with the exact monogamy relation(2)for the smallere,and the tendency becomes more acute,i.e.,most randomly generated states concentrate on the saturation linewhenein finitely tends to a threshold.However,all randomly generated states go away from the saturation line for the biggere,and the multipartite entanglement scores are almost increasing functions ofe.

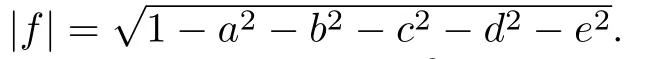
According to Eq.(1),we havethen the inequality(2)is violated.

3 A Counterexample for Regula–Martino–Lee–Adesso-class Conjecture and Its Dynamical Procedure

In Ref.[14],Regulaet al.proposed and investigated a set of sharper monogamy constraints.They raised the intuitive Regula–Martino–Lee–Adesso-class conjecture that the monogamy score from Eq.(2)is amenable to a further decomposition into individualm-qubit contributions in all possible combinations encompassing the focus qubitA1.This leads them to postulate a strong monogamy inequality limiting the distribution of the squared tangleτ2inm-qubit systems,which generally takes the following form(for the four-qubit statesρABCD):

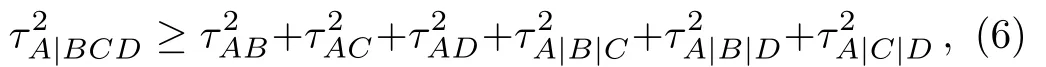
wherecan be used to detect the genuine tripartite entanglement.

For the tangle-based entanglement score,these strong monogamy entanglement scores obey the following relation:

whereis the difference between left and righthand sides of Eq.(6),and is a genuine multipartite entanglement score for the four-partite cases of any fourqubit state.However,these monogamy scores obey another relation[18]as follows,

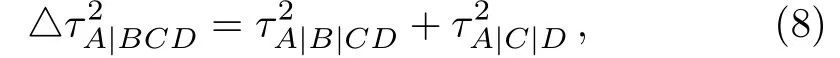
wherefor any four-qubit state.

In this section,we will similarly de fine the multipartite entanglement scores based on the squared entanglement negativityN2and discuss their properties.

3.1 A Counterexample for Squared-Negativity-Based Regula–Martino–Lee–Adesso-class Conjecture

The Regula–Martino–Lee–Adesso-class strong monogamy conjecture has been extensively verified[14]for arbitrary four-qubit pure states when the bipartite entanglement is the tangle.It is still an unsolved problem of how to characterize the entanglement structure in this kind of states for the squared negativity.That is to say,we will discuss whether or not the following strong monogamy relation is always true. The inequality is denoted as the squared-negativity-based Regula–Martino–Lee–Adessoclass monogamy.Now,we similarly apply the differencefrom left and right-hand sides of Eq.(9)to a practical dynamical procedure of a composite system which is composed of two entangled cavity photons being affected by the dissipation of two individualL-mode reservoirs.In fact,the entanglement distribution and the two-qubit residual entanglement,in a composite system consisting of two cavities interacting with independent reservoirs,was firstly analyzed by Baiet al.[19]Taking the negativity as a measure of entanglement,Wanget al.[20]recently proved that the squared-negativity obey the monogamy inequality in 2⊗2⊗4⊗4 cavity-reservoir systems.

The interaction of a single cavity-reservoir system is described by the Hamiltonian[15]

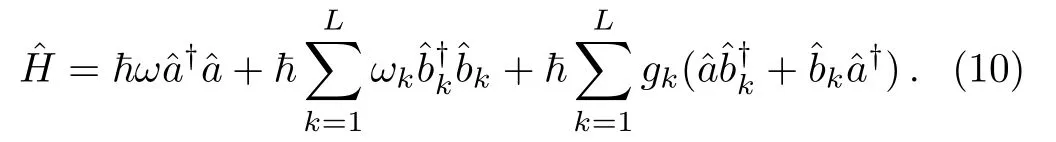
Let the initial state be

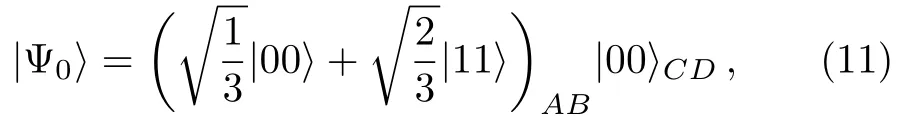
where the initial two cavity photonsABare entangled and the dissipative reservoirsCandDare all in the vacuum states.Then the output state of the cavity-reservoir system has the form[12]

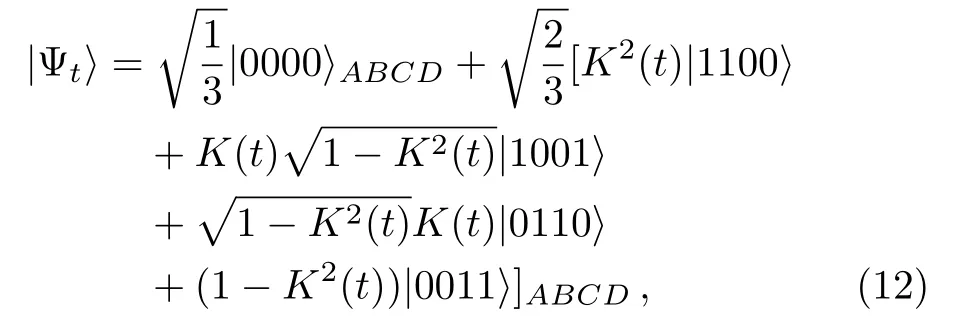
whereis a monotonically decreasing function of the evolution timeκt.

According to Eq.(2),we know that the squared negativity in multiqubit systems is monogamous.However,we will show here that it may be violate the strong monogamy relation.These relations can be seen from Fig.2,which means the squared-negativity-based Regula–Martino–Lee–Adesso-class strong monogamy conjecture does not always hold for the squared entanglement negativity.

As a by-product,an intriguing relation among these multipartite entanglement scores will be derived. Forthese multipartite entanglement scores obey the following relation

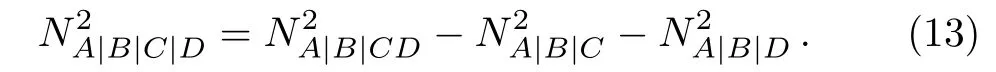
Then we obtain that

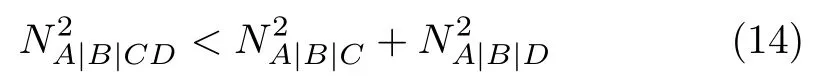
forThen these genuine tripartite entanglement scores based onN2are subadditive.

3.2 Counterexample’s Dynamical Procedure

Forin Eq.(12), the entanglement dynamical property has been discussed in Refs.[14–15,21]when the entanglement measure is quantified by the tangle.However,the multipartite entanglement analysis is mainly based on some specific bipartite partitions in which each party can be regarded as a logic qubit.When either of the parties is not equivalent to a logic qubit,the characterization for multipartite(strong)entanglement structure is an open problem.Fortunately,in this case,we can utilize the entanglement negativity to indicate the genuine multipartite entanglement.For four-qubit states,this kind of entanglement scores in Eq.(13)can be used to detect the genuine four-partite entanglement,which does not come from two-qubit and three-qubit pairs.

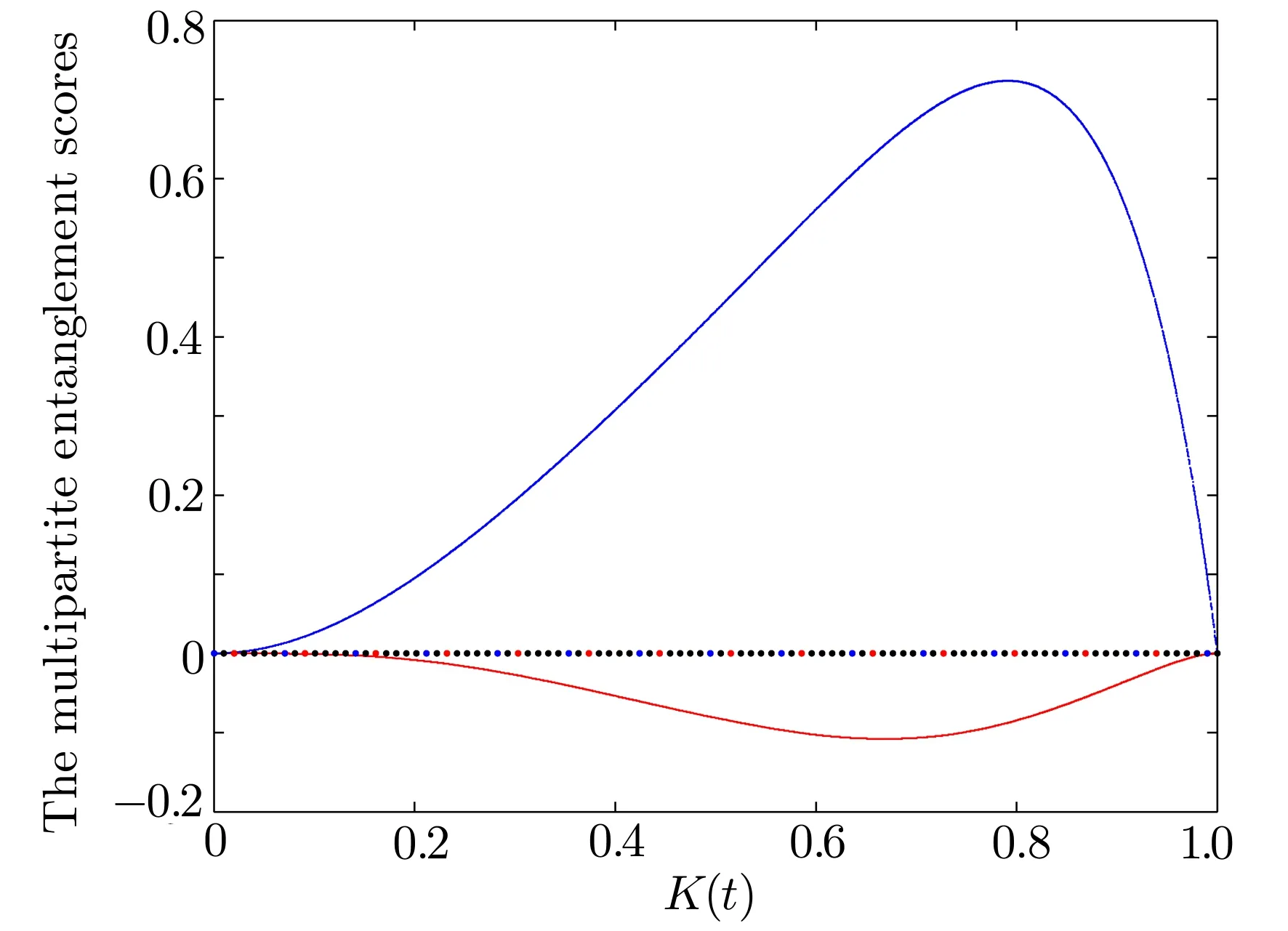
Fig.2 (Color online)The 4-qubit states in Eq.(12)obey the monogamous relation(as shown on the above curve).However,they violate the strong monogamy(as shown on the below curve)for the multipartite entanglement score from Eq.(9).

In Fig.2,we plot the monogamy properties of the squared negativity as functions of the parameterK(t),which is a decreasing functions of the evolution timeκt.It can be found that the squared entanglement negativity is monogamous,whereas it always violates strong monogamous in the four-qubit state.By analyzing the multipartite entanglement structure,we can know how the initial cavity photons entanglement transfers in the multipartite cavity-reservoir system,which provides the necessary information to design an effective method for suppressing the decay of cavity photons entanglement.

From Fig.3(a),we find that in the evolution procedure,the entanglement negativity abruptly becomes zero and remains zero for any other time.However,sudden birth of the negativity arises between the first reservoir and the first cavity photon,and the entanglement is always continuous change as shown in Fig.3(b).Similar behavior has theoretically been reported in Refs.[8,14]for other entanglement measures.

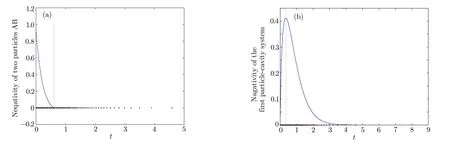
Fig.3 (Color online)(a)The entanglement negativity for the two cavity photons as a function of the evolution time t.(b)The negativity between the first particle and the first cavity as a funtion of t.

Whent∈(0,0.15),we can numerically find that these four-partite entanglement scoresandare all monotonically increasing function of the bipartite entanglementwhereHowever,andare all monotonically increasing functions ofand at the same time they are monotonically decreasing functions ofAs a result,there is no simple dominating relation between multipartite entanglement and few-partite entanglement in composite cavityreservoir systems.

4 Conclusion

We firstly investigate the monogamy properties of the squared entanglement negativity for tripartite higherdimension systems,with a counterexample in 3⊗3⊗3 systems being given by Eq.(4).According to the counterexample,we know that the He–Vidal monogamy conjecture is not always true.Secondly,the squared-negativity-based Regula–Martino–Lee–Adesso-class strong monogamy conjecture can be violated by the counterexample in Eq.(12).More specifically,according to Eqs.(2)and(3),we know that the squared negativity may be always violate strong monogamous even when it is monogamous.As a byproduct,we show that the corresponding genuine tripartite entanglement is subadditive in some four-qubit systems.Finally,we study the entanglement dynamics of two cavity photons in the case of independent reservoirs.Our calculations show that the entanglement between the two cavity photons will suddenly disappear,and there are no simple dominating relations between multi-qubit entanglement and few-qubit entanglement in some time region.

References

[1]C.H.Bennett,H.J.Bernstein,S.Popescu,and B.Schumacher,Phys.Rev.A53(1996)2046.

[2]G.Vidal and R.F.Werner,Phys.Rev.A65(2002)032314.

[3]Y.C.Ou and H.Fan,Phys.Rev.A75(2007)062308.

[4]B.M.Terhal,IBM J.Res.Dev.48(2004)71.

[5]B.Regula,A.Osterloh,and G.Adesso,Phys.Rev.A93(2016)052338.

[6]W.Song,Y.K.Bai,M.Yang,M.Yang,and Z.L.Cao,Phys.Rev.A93(2016)022306.

[7]G.M.Yuan,W.Song,M.Yang,et al.,Sci.Rep.6(2016)28719.

[8]Y.Luo,T.Tian,L.H.Shao,and Y.M.Li,Phys.Rev.A93(2016)062340.

[9]F.Liu,F.Gao,S.J.Qin,S.C.Xie,and Q.Y.Wen,Sci.Rep.6(2016)20302.

[10]Y.K.Bai,Y.F.Xu,and Z.D.Wang,Phys.Rev.Lett.113(2014)100503.

[11]C.Eltschka and J.Siewert,Phys.Rev.Lett.114(2015)140402.

[12]H.He and G.Vidal,Phys.Rev.A91(2015)012339.

[13]V.Co ff man,J.Kundu,and W.K.Wootters,Phys.Rev.A61(2000)052306.

[14]B.Regula,S.Di Martino,S.Lee,and G.Adesso,Phys.Rev.Lett.113(2014)110501.

[15]C.E.L´opez,G.Romero,F.Lastra,E.Solano,and J.C.Retamal,Phys.Rev.Lett.101(2008)080503.

[16]W.K.Wootters,Phys.Rev.Lett.80(1998)2245.

[17]Y.C.Ou,Phys.Rev.A75(2007)034305.

[18]Y.K.Bai,Y.F.Xu,and Z.D.Wang,Phys.Rev.A90(2014)062343.

[19]Y.K.Bai,M.Y.Ye,and Z.D.Wang,Phys.Rev.A80(2009)044301.

[20]L.D.Wang,L.T.Wang,M.Yang,et al.,Phys.Rev.A93(2016)062309.

[21]W.Wen,Y.K.Bai,and H.Fan,Eur.Phys.J.D64(2011)557.

[22]X.Q.Yan and B.Y.Zhang,Ann.Phys.(NY)349(2014)350.