General Quantum Meet-in-the-Middle Search Algorithm Based on Target Solution of Fixed Weight∗
2016-05-10XiangQunFu付向群WanSuBao鲍皖苏XiangWang汪翔andJianHongShi史建红
Xiang-Qun Fu(付向群), Wan-Su Bao(鲍皖苏),Xiang Wang(汪翔),and Jian-Hong Shi(史建红)
Information Engineering University,Zhengzhou 450004,China
Synergetic Innovation Center of Quantum Information and Quantum Physics,University of Science and Technology of China,Hefei 230026,China
1 Introduction
The complexity of Grover’s quantum search algorithm is sub-exponential.Thus the effect of Grover’s optimization algorithm should be thought about the success probability and complexity.Initial state,phase transform,and Hadamard transform,which have different impacts on the success probability and complexity are three elements of Grover’s algorithm.[1−2]And the success probability and complexity are also affected by the percentage of solutions on search space.[3]In 2008,based on the phase shifts,Ref.[4]presented a quantum algorithm,which depicted the relation among the success probability,complexity,arbitrary phase shifts and the number of solutions.
Grover’s quantum algorithm is the search algorithm on quantum computer.And Ref.[5]is the most complete and comprehensive conclusion about quantum search algorithm.However,is it certain that the algorithm for one difficult problem based on Grover’s algorithm is superior to the best classical algorithm?
The complexity of best classical algorithm for knapsack problem isO(n2n/2),[6]wherenis the dimension of knapsack vector.In 1999,based on Grover’s algorithm,the algorithm for knapsack problem was presented,[7]whose complexity and success probability are respectivelyO(c2n/2)and 1−1/2c(cis constant).Compared to the best classical algorithm,the algorithm can not achieve quadratic speedup.Thus,based on the method of combining the classical algorithm for knapsack problem and Grover’s algorithm,how to further reduce the complexity,needs further study.In 2011,we presented the quantum meet-in-the-middle algorithm for knapsack problem,[8]whose computational complexity and storage complexity are respectivelyO(n2n/3)andO(2n/3).
Knapsack public-key encryption schemes[9]are based on the knapsack problem.Merkle–Hellman knapsack encryption scheme was the first concrete realization of a public-key encryption scheme.As its secure basis is superincreasing knapsack problem,it has been demonstrated to be insecure.Many variations have subsequently been proposed,whose knapsack vector density are less than 1.L3-lattice basis reduction algorithm[10]is a polynomial-time algorithm for finding a reduced basis when given a basis for a lattice.In 1991,Schnorr and Euchner presented an improved algorithm.[11]In 1992,Costeret al.gave an algorithm for low density knapsack problem based on lattice basis reduction algorithm.[12]If the density of the knapsack is less than 0.9408,the knapsack problem can be solved with high probability.Thus most variations of the Merkle–Hellman scheme are insecure.
Although the most knapsack public-key crypto are insecure,Chor–Rivest knapsack public-key crypto can resistL3-lattice basis reduction algorithm.[13]And its density of the knapsack vector is 1.077.In 2008,Enciaset al.presented safer parameters for Chor–Rivest crypto,[14]i.e.his a prime,h≤p,11≤h≤31 and 1044 In 2011,Ref.[17]presented the quantum algorithm for searching a target solution of fixed weight,whose core is vector label of fixed weight and label restoration algorithm. De finition 1(Vector label of fixed weight):[17]Suppose that the weight of vectorisd,andaj=0,where 1≤i1 Reference[17]proves that the vectors and their labels are in one-to-one correspondence.According to De finition 1,it is easy to obtain the label of vector,but hard to restore.Reference[17]presented the label restoration algorithm,based on which the corresponding vector of 0≤b≤2t−1 can be obtained in polynomial time.AndIfbis the label of a vector of fixed weightd,then the label restoration algorithm output a vector;otherwise the null vector. Since alln-product vectors of fixed weightdcan be represented by at-product vector,the search space can be reduced,wheretis much smaller thann.And the algorithm is superior to the quantum algorithm only based on Grover’s algorithm. Merkle–Hellman public-key crypto is the first concrete realization of a public-key encryption scheme.[6]Since the knapsack vector with superincreasing nature,it is insecure.However,there are many variations of the knapsack public-key crypto whose density of knapsack vector is lower than 1,they can not resistL3-algorithm. In 1984,Chor and Rivest presented a knapsack public-key crypto,[13]whose density of knapsack vector is more than 1.Based on the Bose–Chowla theorem,the scheme’s decryption is unique.And there is not a polynomial-time algorithm for Chor–Rivest knapsack public-key crypto. Key Generation for Chor–Rivest Public-Key Encryption Each entityAshould do the following: (i)Select a finite fieldFqof characteristicp,whereq=ph,p≥h,and for which the discrete logarithm problem is feasible. (ii)Select a random monic irreducible polynomialf(x)of degreehoverZp.The elements ofFqwill be represented as polynomials inZp[x]of degree less thanh,with multiplication performed modulof(x). (iii)Select a random primitive elementg(x)of the field (iv)For each ground field elementi∈Zp, find the discrete logarithmai=logg(x)(x+i)of the field element(x+i)to the baseg(x). (v)Select a random permutationπon the set of integers(0,1,...,p−1). (vi)Select a random integerd,0≤d≤ph−2. (vii)Computebi=(aπ(i)+d)mod(ph−1),0≤i≤p−1. (viii)A’s public key is((b0,b1,...,bp−1),p,h);A’s private key is(f(x),g(x),π,d). Chor–Rivest Public-Key Encryption Bencrypts a messagemforA,whichAdecrypts. (i)Encryption Bshould do the following: (a)ObtainA’s authentic public key((b0,b1,...,bp−1),p,h). (c)Considermas the binary representation of an integer.Transform this integer into a binary vectorM=(M0,M1,...,Mp−1)of lengthphavingh1’s as follows: (c1) (c2)Forifrom 1 topdo the following: (e)Send the ciphertextctoA. (ii)DecryptionTo recover plaintextmfromc,Ashould do the follwing: (a)Computer=(c−hd)mod(ph−1). (b)Computeu(x)=g(x)rmodf(x). (c)Computes(x)=u(x)+f(x),a monic polynomial of degreehoverZp. (e)Compute a binary vectoras follows.The components ofMthat are 1 have indicesThe remaining components are 0. (f)The messagemis recovered fromMas follows: (f1)Set (f2)Forifrom 1 topdo the following: According to the decryption way of Chor–Rivest knapsack public-key encryption,ifMcan be solved byc,b0,b1,...,bp−1,the messagemcan be easily obtained. In 2008,Encinas etc.gave four conditions for choosing the parameter of the Chor–Rivest scheme,[14]i.e.h≤p,11≤h≤31,1044 The quantum meet-in-the-middle algorithm is used to attack Chor–Rivest scheme,whose computational and storage complexity are respectivelyO(2p/3p)andO(2p/3). Based on the target solution of fixed weight,Refs.[15]and[16]respectively present an improved quantum meetin-the-middle algorithm,which does not have a generic.The reason is as follow: The main idea of the quantum meet-in-the-middle algorithm is searching a collision.In Refs.[15]and[16],allf1should be stored.Then searchingf2satisfiesf=f1+f2(fis the key of NTRU,which is a polynomial of fixed weightdf.f1andf2are both a polynomial of fixed weightdf/2).If the solution of one problem is a vector(x0,x1,...,xn−1)of fixed weighta. Suppose storing all vectors(x0,x1,...,xk). Then one solution can be obtained by searching(xk+1,xk+2,...,xn−1).But we can not suppose that the weight of(x0,x1,...,xk)and(xk+1,xk+2,...,xn−1)are botha/2.Thus the algorithm of Refs.[15]and[16]do not have a generic.And giving a general algorithm is worth further study. Theorem 1Supposing 1 ProofTo prove the theorem,we only need to prove thatt1=t2,wheret1is the number ofXj=(x1,x2,...,xn),t2is the number of elements of the setAand It is obvious that each element ofAis the solution of the knapsack problem. If(x1,x2,...,xk)and(xk+1,xk+2,...,xn)satisfy Thust1=t2and we can obtain theorem 1. According to theorem 1,the knapsack problem solving is equal to two knapsack problems solving,whose dimension of the knapsack vector are both smaller. If the weight of(x1,x2,...,xn)isd,the sum of the weight of(x1,x2,...,xk)and(xk+1,xk+2,...,xn)isd. Supposing the Oracle iswhich satisfies where the weight ofisd−jand 0≤j≤d.The algorithm of constructingLjis given below. The Algorithm of ConstructingLj Step 1Suppose Step 2Exhaustively search allt′-product Boolean vector(a0,a1,...,at′−1); The complexity of the label restoration algorithm isO(k),and Step 2 need be run for 2t′iterations.Thus the complexity of the algorithm is Furthermore,the general quantum meet-in-the-middle search algorithm based on the target solution of fixed weight can be obtained. General Quantum Meet-in-the-Middle Search Algorithm Based on the Target Solution of Fixed Weight Step 1Selectk,whered≤k≤[n/2]; Step 3Forj=0,1,...,d,do the following operation (a)Give two quantum registers whose initial state are respectivelyandAnd2u}. (b)The Hadamard transform is used to put the first register into equal superposition state|s′⟩, (c)Use Grover’s algorithm to search for t-product Boolean vectorsb=(b0,b1,...,bt−1). (d)Use the label restoration algorithm to calculate the(n–k)-product Boolean vectorv0=(xk,xk+1,...,xn−1)corresponding to labelb=(b0,b1,...,bt−1). NoteGrover’s algorithm can be replaced by the algorithm of Ref.[18]. We assumed≤n/2.Ifd>n/2,the algorithm only needs to search the vectorof fixed weightn−dwhich satisfywhereand⊕is modulo-2 adder operation. We now analyze the algorithm. Thestoragecomplexity ofStep 2isAnd the computational complexity of sortingLjisThus the computational complexity of sortingL0,L1,...,Ldis Theorem 2Supposing 0 Proof Thus we can obtain theorem 2. Since when 0 Then If Since thus the computational complexity and storage complexity of the algorithm are respectivelyO(n2n/5)andO(2n/5). NoteIfk=[n/2]andd≤[n/20],kH(d/k)<0.2n.According to the safer parameters for Chor–Rivest crypto,the algorithm can be applied to attack Chor–Rivest crypto,whose computational complexity isO(p2p/5).And the value ranges ofhandpare shown in Table 1. Thus,compared with the quantum algorithm for searching a target solution of fixed weight,its storage complexity is higher,but computational complexity is smaller;compares with the quantum meet-in-the-middle algorithm,the computational and storage complexity are both smaller.And the success probability of these algorithms are allO(1).The conclusion can be shown in Table 2. Table 1 Value ranges of h and p,where the symbol“–” means that there are no h and p,which satisfy h/p≤1/20. Table 2 Comparison between new algorithm and other algorithms. For differentk,the computational complexity is also different.Theorem 3 will show the optimal value ofk. Theorem 3X=(x0,x1,...,xn−1)of fixed weightdis the knapsack vector,whered≤[n/2].Supposing andIfk=k0,the computational complexity of the general quantum meet-in-the middle search algorithm based on the target solution of fixed weight is the least;otherwisek=d.Andk0satisfies ProofSuppose It is obvious thatf1(k)andf2(k)are respectively monotone increasing function and monotone decreasing function on[d,n−d+1].Furthermore,is monotone increasing function. (i)Whenthere iswhich satisfy for arbitraryd≤k≤n−d+1. Thus,the computational complexity of the algorithm is the least whenk=k0. (ii)Iff1(d)≥f2(d),the computational complexity of the algorithm is the least whenk0=d,i.e. Thus we can obtain theorem 3. Theorem 3 shows the optimal value ofk,which can be easily obtained whenn,dare known. In this paper,the general quantum meet-in-the-middle search algorithm based on the target solution of fixed weight is presented,which can be applied to attack Chor–Rivest public-key crypto.Compared with the existed algorithm,its computational complexity is lower. References [1]D.Biron,O.Biham,E.Biham,M.Grassl,and D.A.Lidar,Phys.Rev.A60(1999)2742. [2]L.K.Grover,Phys.Rev.Lett.80(1998)19. [3]M.A.Nielsen and I.L.Chuang,Quantum Computation and Quantum Information,Cambridge University Press,Cambridge(2000). [4]P.Zhong and W.Bao,Chin.Phys.Lett.25(2008)8. [5]F.M.Toyama,W.Dijk,and Y.Nogami,Quantum.Inf.Process.12(2013)5. [6]A.J.Menezes,P.C.V.Oorschot,and S.A.Vanstone,Handbook of Applied Cryptography,CRC Press LLC,Boca Raton(1997). [7]J.Hu,G.Chen,and G.Guo,Chin.J.Comput.22(1999)12,(in Chinese). [8]W.Bao,Z.Song,P.Zhong,and X.Fu,Acta.Electr.Sin.39(2011)1,(in Chinese). [9]R.C.Merkle and M.E.Hellman,IEEE.T.Inform.Theory.24(1978)114. [10]A.K.Lenstra,H.W.Lenstra,and L.Lovasz,Math.Ann.261(1982)515. [11]C.P.Schnorr and M.Euchner,Fundamentals of Computation Theory(LNCS)529(1991)68. [12]J.M.Coster,A.Joux,B.A.LaMacchia,et al.,Comput.Complex.2(1992)111. [13]B.Chor and R.L.Rivest,A Knapsack Type Public Key Cryptosystem Based on Arithmetic in Finite Fields,Advances in Cryptology:Proceedings of CRYPTO 84,Santa Barbara(1984). [14]L.H.Encinas,J.M.Masque,and A.Q.Dios,Comput.Math.Appl.56(2008)11. [15]Z.Xiong,J.Wang,Y.Wang,T.Zhang,and L.Chen,Int.J.Security and Its Applications6(2012)2. [16]H.Wang,Z.Ma,and C.Ma,Chinese Sci.Bull.58(2013)28. [17]X.Wang,W.Bao,and X.Fu,Chinese Sci.Bull.56(2011)6. [18]G.Long,Phys.Rev.A64(2001)2.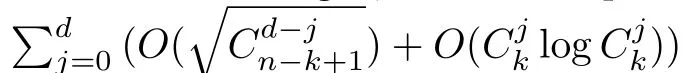
2 Quantum Algorithm for Searching a Target Solution of Fixed Weight
3 Chor–Rivest Public-Key Crypto
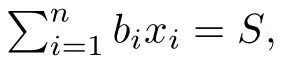
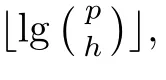
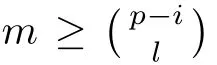

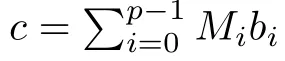
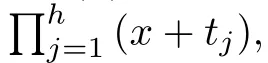
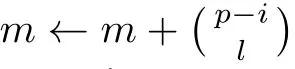
4 General Quantum Meet-in-the-Middle Search Algorithm Based on Target Solution of Fixed Weight
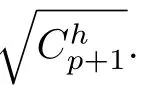
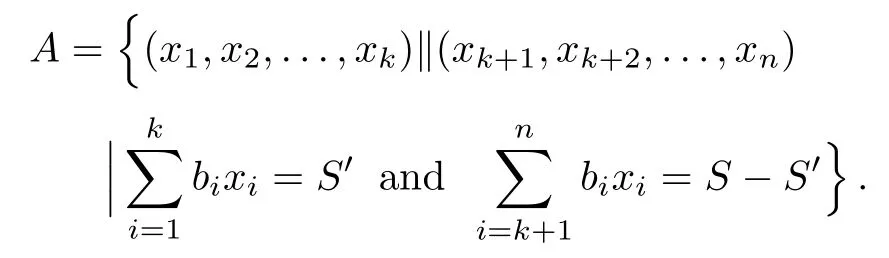
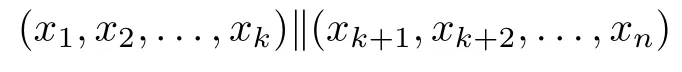

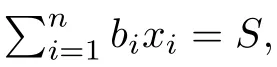
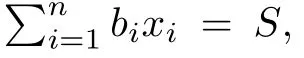
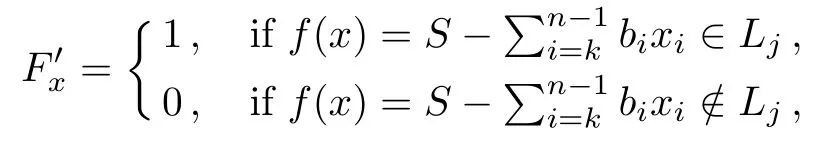
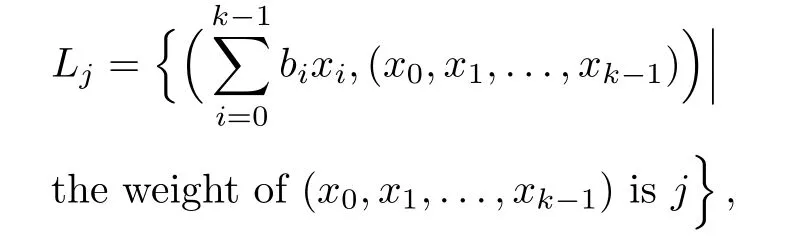
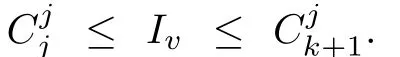
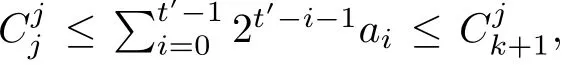
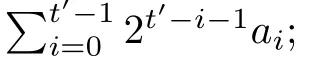
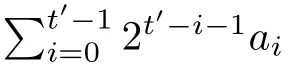

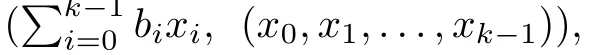
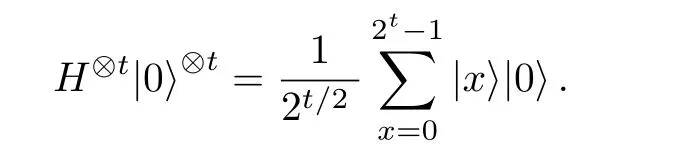
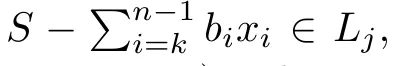
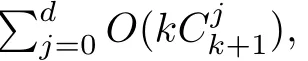
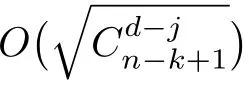
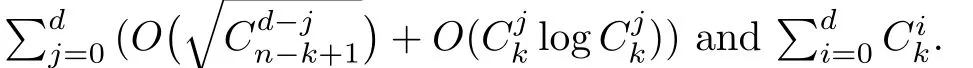


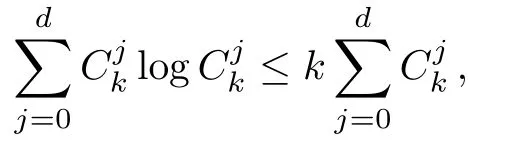
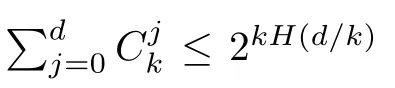
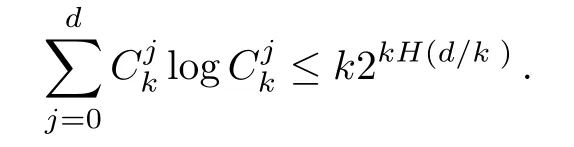
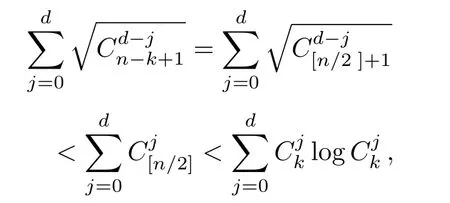


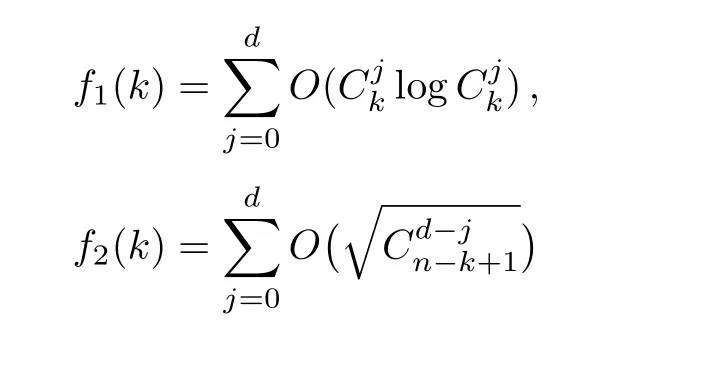
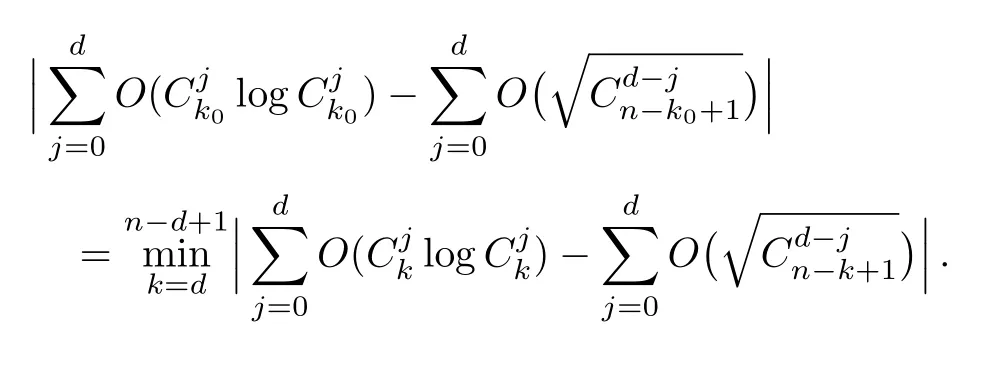
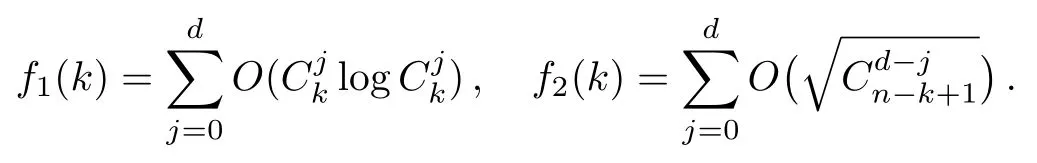
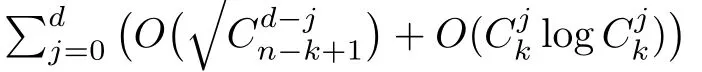
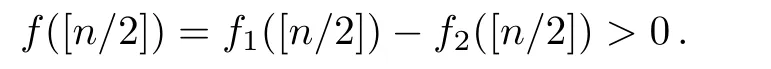
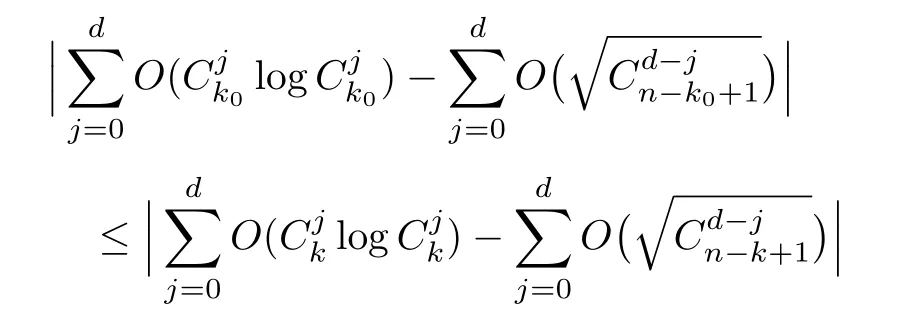
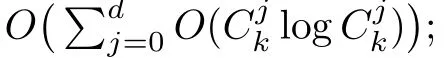
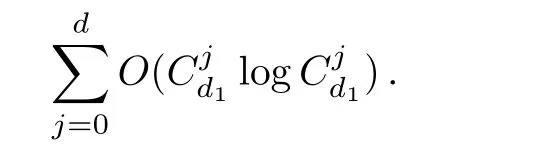
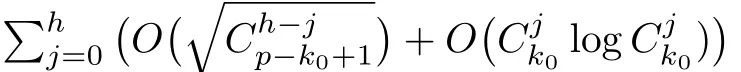
5 Conclusion
杂志排行
Communications in Theoretical Physics的其它文章
- E ff ect of Mis fit Strain on Pyroelectric Properties of(111)Oriented Pb(Zr1−xTix)O3 Thin Films∗
- In fluence of Defects and Crystallographic Orientation on Mechanical Behavior of Nanocrystalline Aluminium∗
- Critical Behavior of Spatial Evolutionary Game with Altruistic to Spiteful Preferences on Two-Dimensional Lattices∗
- First-Principles Study of Structural,Magnetic,Electronic and Elastic Properties of PuC2∗
- Study of Friction between Liquid Crystals and Crystalline Surfaces by Molecular Dynamic Simulations∗
- Relativistic Correction on Neutrino Emission from Neutron Stars in Various Parameter Sets∗
