Quasi-one Dimensional Topological Insulator:M¨obius Molecular Devices in Peierls Transition∗

Zhi-Rui Gong(龚志瑞)Zhi Song(宋智)and Chang-Pu Sun(孙昌璞)†

1College of Physics and Energy,Shenzhen University,Shenzhen 518060,China

2Beijing Computational Science Research Center,Beijing 100084,China

3Department of Physics,Nankai University,Tianjin 300071,China

1 Introduction

Topological insulator(TI),as an exotic bulk insulator with robust metallic surfaces described by zero modes,has been extensively studied.[1−15]Many candidates of TI are of more than one dimension,such as two-dimensional HgCdTe quantum wells with helical zero modes[16−18]or the quasi-one dimensional graphene ribbon.[19−20]It seems impossible to find one-dimensional TI,since a onedimensional system only possesses eitherR1orS1geometry respectively with the open boundary condition or periodic boundary one.However,with some lattice deformations,many-electron systems in one dimension can display spooky natures,to which the Peierls instability induced by electron-phonon interaction takes responsibility.[21−22]

In this letter,we are challenged to discovery a quasione dimensional(Q1D)TI,where the soliton due to Peierls transition emerges as a zero mode.In generic system with this transition,e.g.,the usual polyacetylene chain by the Su–Schrieffer–Heeger(SSH)model,[23]however,the zero mode is not a ground state,thus not robust.Our present task is to force the solitonary zero mode to become a ground state by invoking a non-trivial topology of con figuration spaces.This kind of systems can be implemented as experimentally accessible M¨obius molecular devices,[24−30]and described as tight binding electronic models on the M¨obius ladder lattice(see Fig.1(a)).Actually,it has been shown that there exist observable topological effects,such as the topological cutoff of the transmission spectrum[31]through a non-abelian induced gauge field.The existence of the zero modes in such systems is the consequence of both the electron-phonon interaction and the M¨obius boundary condition.It should be indicated that such zero modes actually are protected by theZ2topology of the M¨obius strip in the real space,while the widely studied topological properties in solid state physics emerge in the momentum space.

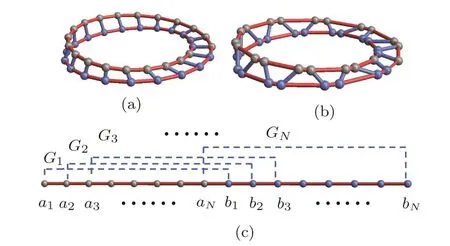
Fig.1 (Color online)Schematic illustrations of(a)undimerized ladder with M¨obius boundary condition,(b)dimerized ladder with M¨obius boundary condition and(c)the corresponding one-dimensional version of M¨obius ladder system with long range coupling.

2 Peierls Transition of M¨obius Molecular Devices

The topological molecular device we consider consists of electrons hopping on a M¨obius ladder(see Fig.1(a)),which is a non-orientable manifold,whose edge de fines a two-point bundle overS1and thus Z2topological structure.Figure 1(b)shows one of its possible lattice deformations.

∗Supported by the National Natural Science Foundation of China under Grant No.11504241 and the Natural Science Foundation of Shenzhen University under Grant No.201551

†E-mail:cpsun@csrc.ac.cn

The corresponding Hamiltonian reads

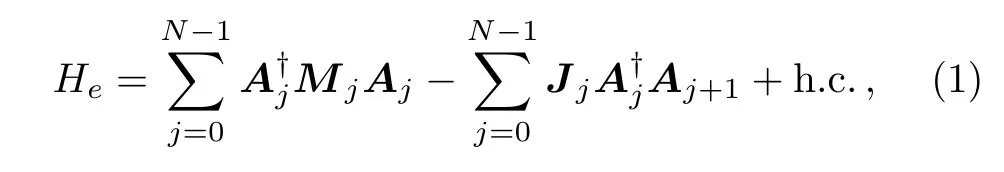
where operator-value vectorAj=(aj,bj)Tis defined in terms of the annihilation operatorajandbjpictured as Fig.1(c).Here,the M¨obius ladder can be regarded as a Q1D system,consisting ofa-chain andb-chain with long range hopping with strengthGj≡G0,forj=0,1,...,N−1.Here,Nis the site number ofa-chain(bchain).The transition matricesandJj=JjIare defined by Pauli matricesσx,σyandσz,unity matrixI,on-site energy differenceεj≡ε0and hopping strengthJj≡J0.Particularly,the boundary conditionAN=σxA0is taken to reflect the M¨obius twist.The pure electron system is diagonalized to show two bands(Fig.2(a)).

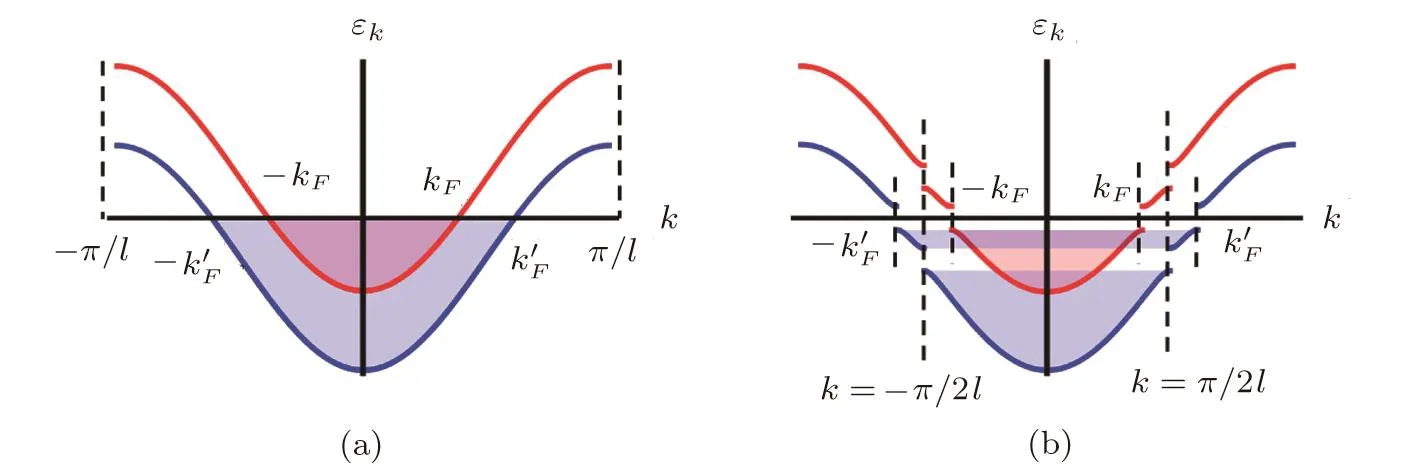
Fig.2 (Color online)Schematic spectra of ladders without dimerization(a)and with staggered dimerization(b).The shadow regions represent the electron occupation in the energy bands.

Peierls transition induced by electron-phonon interactions in such a Q1D system,we use the Born–Oppenheimer approximation by presuming the transverse and longitudinal lattice deformations(see Fig.3)depicted by two displacementsujandvj.Here,the lattice deformation is modeled as 2Ncoupled harmonic oscillators with HamiltonianHp({uj,vj}).

There exist five dimerization patterns illustrated in Fig.3,including three simple dimerizations and two hybrid dimerizations.Letmandlbe the lattice constants along the transverse and longitudinal directions,respectively,and we can de fine the static uniform deformationsuj=(−1)jδandvj=(−1)jσ.They characterize the rung dimerization(Fig.3(b)),the columnar dimerization(Fig.3(c)),the staggered dimerization(Fig.3(d)),vertical saw-tooth(Fig.3(e))and inclined saw-tooth(Fig.3(f)).

For a given lattice deformation,we diagonalize the electronic Hamiltonian to obtain the total energy from the Born–Oppenheimer approximation.We consider the staggered dimerization(Fig.3(b))described byJj=withlj=l+(−1)i+jσ,whereα(β)is the rate of changes of the longitudinal(transverse)hopping.Then four separate bands are obtained as

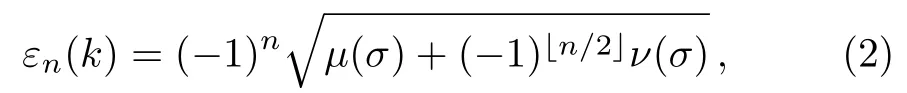
where forn=1,2,3,4,

forandrepresents the integer part ofn/2.

It follows the energy band diagram(Fig.2(b))that the deformation opens four gaps in the original two overlapped bands.The two gaps atare usual because they only arise from the longitudinal deformation forachain andb-chain,respectively.The other two gaps at Fermi momentumin the upper band andin the lower band arise from the coupling between thek-states ina-chain and thestates inb-chain with strengthapproximately.

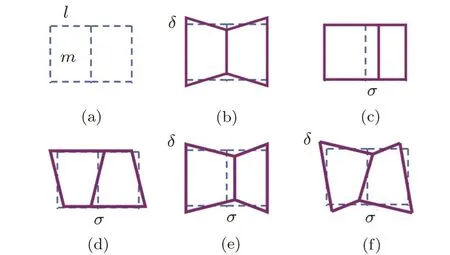
Fig.3 (Color online)Schematic illustration of the dimerization patterns including(a)original lattice,(b)transverse,(c)columnar,(d)staggered,(e)vertical sawtooth,and(f)inclined saw-tooth.m and l are the lengths of transverse and longitudinal directions,respectively.δ and σ denote the static deformations along transverse and longitudinal directions,respectively.

Next,we only consider the monovalent case that 2Nelectrons fill in all the negative energy levels. Apparently,the conventional gaps athave not obvious Effect on the conducting properties of the elec-trons because they are below the deformed Fermi surface.The gaps opened at Fermi surfaces may decrease the energy of the electrons bywhereandE(0)is the energy without dimerization.The lattice deformation also increases the energy of phonons bywhereKtandKlare spring constants of transverse and longitudinal directions,respectively.The minimization of the total energy∆E=∆Ep+∆Eedetermines a stable con figuration with a phase diagram.The above calculation is carried out for the staggered case,but repeating it for all deformations(Fig.3)gives the total Peierls phase diagrams for the generic boundary condition(Fig.4(a))and M¨obius one(Fig.4(b)).Here,the parameters are chosen as,andl=m.

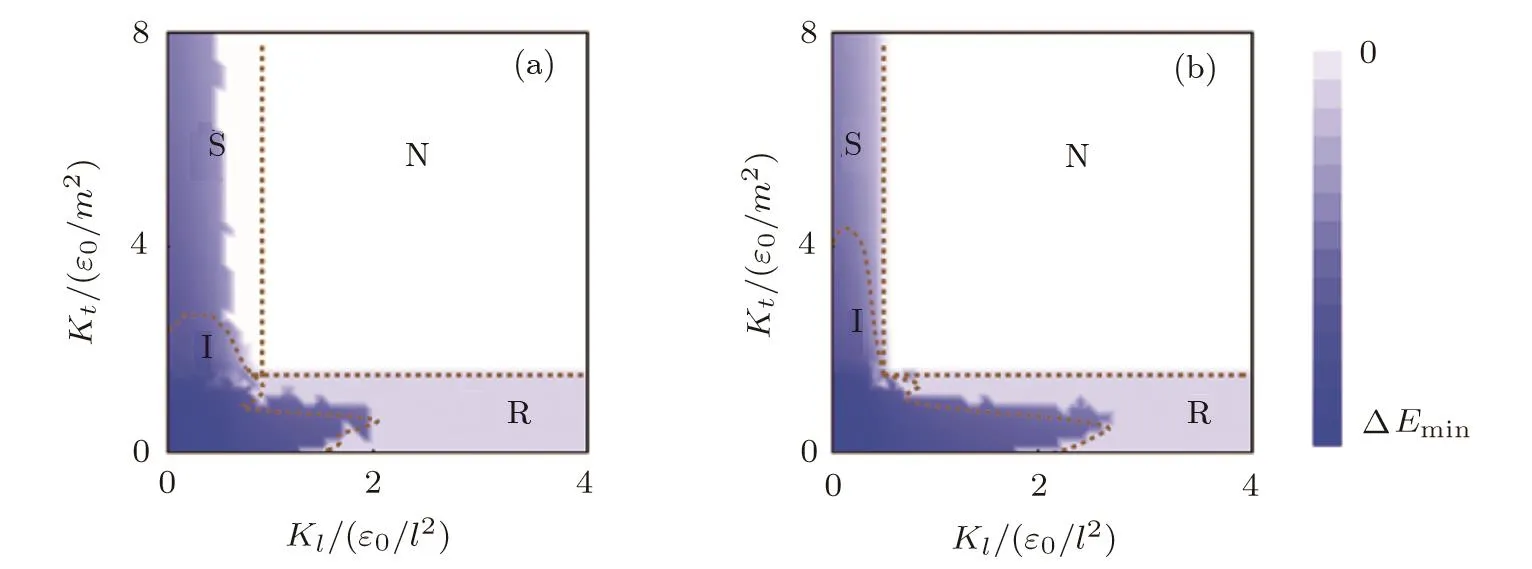
Fig.4(Color online)The phase diagrams of the ladder system with(a)the generic and(b)the M¨obius boundary conditions,which are plotted versus(Kl,Kt)in(a)and(b),respectively.The parameters are chosen as G0=15ε0,J0=10ε0,α = β = ε0/m,and l=m.The distribution of the total energy ∆E versus(Kl,Kt)determines the phases boundaries,which are plotted as dashed lines.The capitalized letters “S”,“I”,“R”,and “N”,represent the staggered,the inclined saw-tooth,rung,and no dimerization,respectively.

The region of staggered dimerization pattern under the M¨obius boundary condition shrinks comparing with the generic one.This fact means that metal phase is preferable for a M¨obius ladder system.Therefore,the above phase diagrams show that the conducting properties can be dramatically changed when the topology of the ladder is switched.To further consider the topological effect on conducting properties,the existence of zero modes will be revisited for our Q1D system.

3 Continuum Model

We adapt the continuous field approach by regarding the M¨obius ladder as a one-dimensional system with long range hopping(Fig.1(c)).Without loss of generality,we focus on the special caseε0=0.For a continuous field approach,it is crucial to introduce an order parameter∆(x)=−4αu(x),whereu(x)is the continuous limit of displacements(−1)juj.

The Hamiltonian of continuum modelH=He+Hpcontains the phonon part

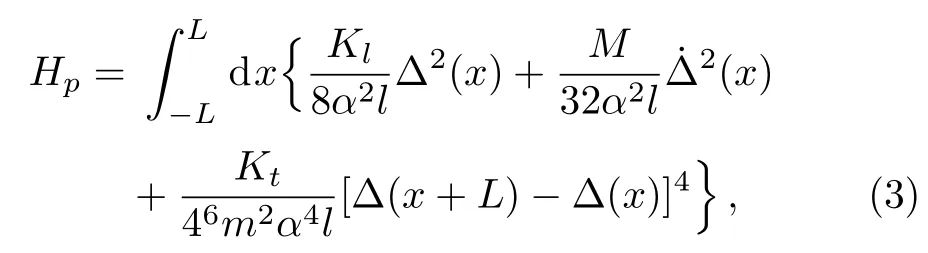
and the electron part

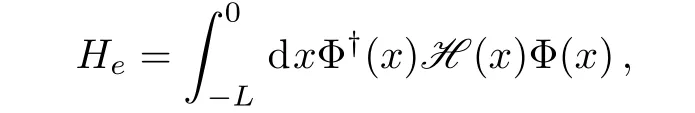
whereMis the mass of the single particle andis the length of thea-chain(b-chain),which approaches infinity at the end of calculation.In the electron part,the hopping electron could be described with a 4-component spinorPhysically,respectively represent the left-traveling waves and right-traveling waves ina-chain(b-chain).In this spinor representation,the Hamiltonian density is expressed asσx,σyandσz,

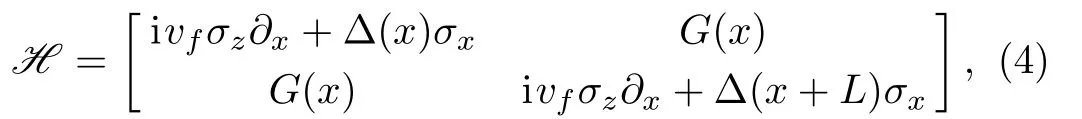
wherevf=2lJ0,andL)]2/(32mα2)is effective coupling between thea-chain andb-chain.

To reflect the M¨obius boundary condition in our Q1D model(Fig.1(c)),we take the period 2Lfor boundary conditionsrather thanLfor the generic case. With this boundary condition,we solve the Bogoliubov-de Gennes(BdG)equationwhereirepresents thei-th energy band of the spectrum andAt zero temperature,the order parameter∆(x)satisfies the self-consistent equations

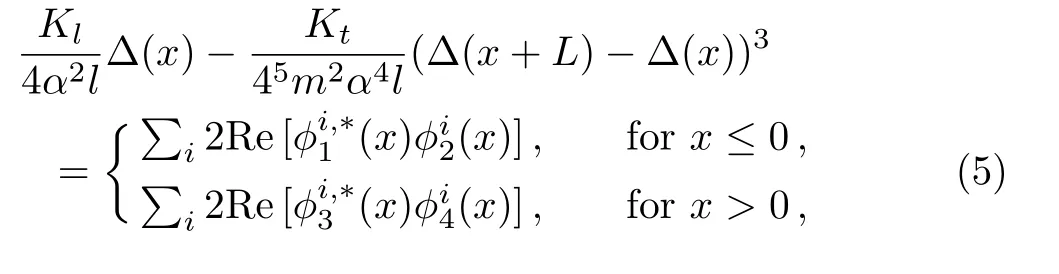
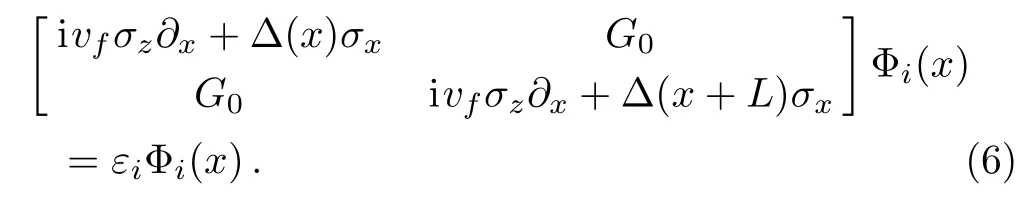
To solve the above equation,we apply a unitary transformation aswhere the transformed wavefunction are defined as

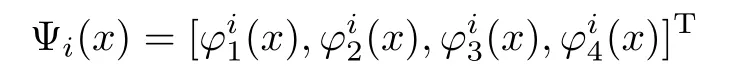
and the unitary matrix is

4 Zero Modes for Topological Insulator

As we show as follows,some solutions of the above BdG equation can exist as zero modes.When they happen to be ground state and robust under external perturbations,the M¨obius system then becomes a topological insulator.

In the following,we only consider the caseKl≪Kt. In this case,three dimerization patterns of rung(Fig.3(b)),vertical-saw tooth(Fig.3(e))and inclined saw-tooth(Fig.3(f))occur rarely.Thus we only need to compare the energy of staggered with columnar one.Let us first revisit M¨obius ladder system with the staggered dimerization characterized byIn this phase,the order parameters ina-andb-chains are opposite and display a Peierls phases domain wall.We also notice that the columnar dimerization to be compared is characterized by

For the staggered case,we assume a kink deformation∆(x)= Γtanh(x/ξ)withξ=vf/Γ,which is so small that the effective coupling between thea-andb-chain asIn this sense,the BdG equation is written as

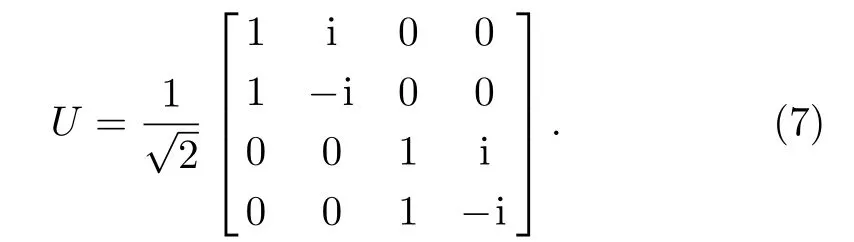
After the transformation,the BdG equation for Ψi(x)becomes

As the solutions of the BdG equation with energyεi=0,two degenerate solitonary statesand(illustrated in Fig.5(a)as the middle lineεs=0)can be found as one with non-vanishing componentsand another with non-vanishing componentsfor These solitonary states are teneric ladder,the existencehe zero modes existing at the midgap.Since there is no such solitonary state in the g of the solitons is absolutely topological effect.

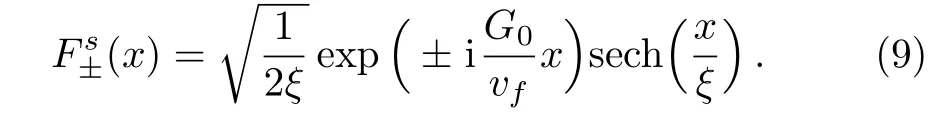
We note that the another two bands(illustrated in Fig.5(a)as two overlapped shadowed domains)fully occupied by the electrons correspond to eigen functions

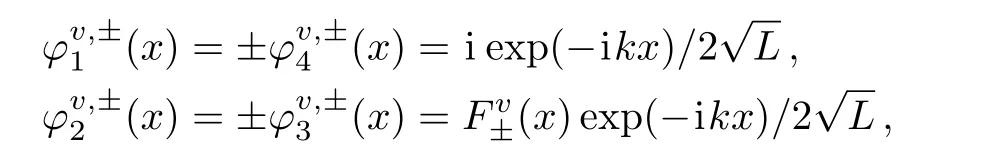
where

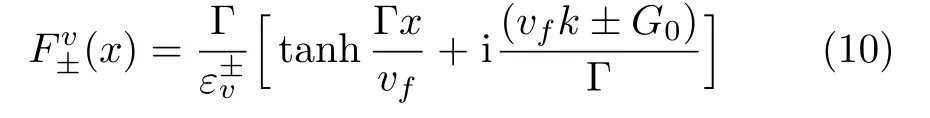
represents a deviation from a plane wave in the kink order.Then,it follows from the self-consistent equations Eq.(5)that

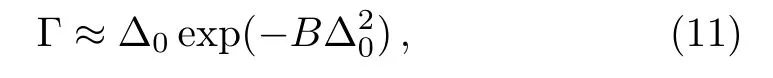
whereis the order parameter for onedimensional uniformly dimerized system,andwithkfis the Fermi momentum.

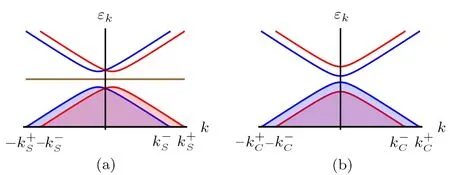
Fig.5 (Color online)Schematics of the energy spectra of the valence bands under(a)staggered and(b)columnar dimerizations,whereandThe shadow regions represent the electron occupation in the energy bands,and the brown straight line represents the solitonary states.

Moreover,we can further prove that the above solitonary states are the ground states. To this end we calculate the total energy of the electron-phonon systemaccording to the phase shift[22]of the eigen-functionsarctanA straightforward algebra explicitly gives

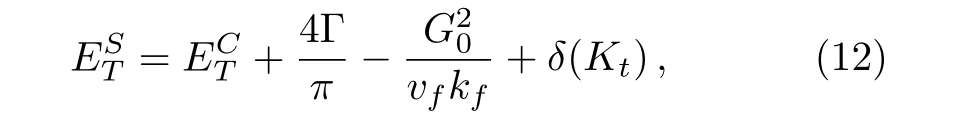
whereis the total energy for the columnar dimerization(Fig.3(c)),andresults from the coupling between thea-andb-chain.The second term inis usual energy increment due to the exitance of solitonary states.The third term inresults from the difference in the total energies in two filling ways.One corresponds to the staggered dimerization(Fig.5(a))with two lower bandsoccupied by electrons,while the other corresponds to columnar one(Fig.5(b))with two lower bandsoccupied.For the latter the energy of electrons increases because a part of electrons are forced to occupy higher energy levels.IfG0is so large thatis negative,the ground state of the M¨obius ladder system corresponds to the staggered dimerization rather than the columnar one.In this case the solitonary states are zero modes existing as the ground state.

Actually,the topology of the system can protect the solitonary state from external perturbations.For example,when the soliton propagates along the longitudinal directions without spreading,the energy increment caused by moving soliton with velocityvsfrom the time evolution of order parametertanhiswhich could be much smaller than the exciting energyδE.Since the moving soliton is robust and charged,the M¨obius ladder with staggered dimerization is actually electrically conductive.

5 Conclusion

We have shown that the M¨obius molecular devices assisted by Peierls instability could be regarded as the simplest example of topological insulator.When the M¨obius boundary condition is applied to the ladder system,the solitonary solutions emerge in such a quasi-one dimensional system as ground state in the Peierls phases domain wall.The existence of the zero modes is the consequence of both the electron-phonon interaction and the M¨obius boundary condition.The electron-phonon interaction causes the dimerization and the transporting solitonary states.The M¨obius boundary condition just guarantees that the solitonary solutions are the ground state.Such zero modes actually are protected by theZ2topology of the M¨obius strip in the real space,while the widely studied topological properties in solid state physics emerge in the momentum space.As the charged zero modes propagating without spreading,the conducting properties of the M¨obius molecular devices are pretty dramatic for topological insulator.

Acknowledgments

The authors thank Nan Zhao for helpful discussion.

References

[1]M.Z.Hasan and C.L.Kane,Rev.Mod.Phys.82(2010)3045.

[2]X.L.Qi and S.C.Zhang,Phys.Today63(2010)33.

[3]J.E.Moore,Nature(London)464(2010)194.

[4]X.L.Qi and S.C.Zhang,Rev.Mod.Phys.83(2011)1057.

[5]S.C.Zhang,Physics1(2008)6.

[6]L.Fu,C.L.Kane,and E.J.Mele,Phys.Rev.Lett.98(2007)106803.

[7]L.Fu and C.L.Kane,Phys.Rev.B76(2007)045302.

[8]J.C.Y.Teo,L.Fu,and C.L.Kane,Phys.Rev.B78(2008)045426.

[9]J.E.Moore,Y.Ran,and X.G.Wen,Phys.Rev.Lett.101(2008)186805.

[10]X.L.Qi,T.L.Hughes,and S.C.Zhang,Phys.Rev.B78(2008)195424.

[11]A.M.Essin and J.E.Moore,Phys.Rev.B76(2007)165307.

[12]H.Obuse,et al.,Phys.Rev.B78(2008)115301.

[13]Y.Ran,Y.Zhang,and A.Vishwanath,Nat.Phys.5(2009)298.

[14]J.Li,et al.,Phys.Rev.Lett.102(2009)136806.

[15]A.Bermudez,et al.,Phys.Rev.Lett.102(2009)135702.

[16]B.A.Bernevig,T.L.Hughes,and S.C.Zhang,Science314(2006)1757.

[17]M.K¨onig,et al.,Science318(2007)766.

[18]J.E.Moore and L.Balents,Phys.Rev.B75(2007)121306(R).

[19]Z.L.Guo,et al.,Phys.Rev.B80(2009)195310.

[20]Z.L.Guo,Z.R.Gong,and C.P.Sun,arXiv:0904.2231(2009).

[21]W.P.Su,J.R.Schrie ff er,and A.J.Heeger,Phys.Rev.Lett.42(1979)1698.

[22]H.Takayama,Y.R.Lin-Liu,and K.Maki,Phys.Rev.B21(1980)2388.

[23]W.P.Su,J.R.Schrie ff er,and A.J.Heeger,Phys.Rev.Lett.42(1979)1698.

[24]V.Balzani,A.Credi,and M.Venturi,Molecular Devices and Machines:A Journey Into the Nanoworld,Wiley-VCH Verlag GmbH&Co.KGaA,Weinheim(2003).

[25]A.Nitzan and M.A.Ratner,Science300(2003)1384.

[26]K.Burke,R.Car,and R.Gebauer,Phys.Rev.Lett.94(2005)146803.

[27]C.Zhang,et al.,Phys.Rev.Lett.92(2004)158301.

[28]M.J.Comstock,et al.,Phys.Rev.Lett.99(2007)038301.

[29]A.LaMagna and I.Deretzis,Phys.Rev.Lett.99(2007)136404.

[30]C.Q.Wu,J.X.Li,and D.H.Lee,Phys.Rev.Lett.99(2007)038302.

[31]N.Zhao,et al.,Phys.Rev.B79(2009)125440.