A New Integrable(2+1)-Dimensional Generalized Breaking Soliton Equation:N-Soliton Solutions and Traveling Wave Solutions

Abdul-Majid Wazwaz

Department of Mathematics,Saint Xavier University,Chicago,IL 60655,USA

1 Introduction

The nonlinear equations describe the real features in a variety of science and engineering areas,such as fluid mechanics,theory of solitons,hydrodynamics,optical fibers,chaos theory and chemical physics,etc.The studies on nonlinear equations are flourishing in the past decades.Moreover,studies of finding soliton solutions of the nonlinear equations attract researchers to develop more methods and progress in this area.Towards these studies,a variety of powerful methods to construct multiple soliton solutions and traveling wave solutions has been established in science and engineering domains.[1−21]Examples of the methods that have been used are the Hirota bilinear method,[4]the simplified Hirota method,[5]the B¨acklund transformation method,Darboux transformation,Pfaffian technique,the inverse scattering method,the Painlev´e analysis,the generalized symmetry method,the subsidiary ordinary differential equation method,the coupled amplitude-phase formulation,the sine-cosine method,the sech-tanh method,the mapping and the deformation approach,and many other methods.[11−19]The Hirota bilinear method,[4]and the simplified Hirota method developed in Ref.[5]are rather heuristic and significant to handle equations with constant coefficients.Once a soliton equation is transformed into bilinear forms through a dependent variable transformation,then the N-soliton solution can be obtained systematically.The computer symbolic systems such asMapleandMathematicaallow us to perform complicated and tedious calculations.

The interactions between soliton solutions for integrable models are considered to be completely elastic.[1−7,20−21]By elastic interactions we mean that if a soliton meets another soliton of its kind,they interact,but without destroying each other identities.That is to say,the amplitude,velocity and wave shape of a soliton do not change after the non-linear interaction.[8−21]However,as for some soliton models,completely non-elastic interactions will occur when specific conditions between the wave vectors and velocities are satisfied such as in compactons.For instance,at a speci fic time,one soliton may fission to two or more solitons;or on the contrarily,two or more solitons will fusion to one soliton.[9]We call these two types of phenomena soliton fission and soliton fusion respectively.In fact,for many real physical models(such as in organic membrane and macromolecule material,[9]in SrBaNi oxidation crystal and waveguide,[9]in even-clump DNA and in many physical fields like plasma physics,nuclear physics,hydrodynamics and so on,people have observed the phenomena soliton fusion and soliton fission.[20−21]

A variety of solutions of distinct features appear in solving nonlinear equations.Traveling waves appear with physical features in solitary wave theory such as solitons,kinks,peakons,cuspons,rogue waves,complexitons,positons,negatons,and compactons and many others.[20−21]Solitons are localized traveling waves which are asymptotically zero at large distances.

It is well known that the(2+1)-dimensional breaking soliton equation reads[21]

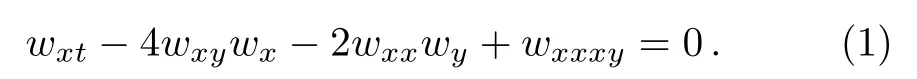
This equation was used to describe the(2+1)-dimensional interaction of Riemann wave propagated along they-axis with long wave propagated along thex-axis.[1−2,21]A class of overturning soliton solutions has been introduced in Refs.[1,21].Fory=x,and by integrating the resulting equation in Eq.(1),the equation is reduced to the KdV equation.

A new(2+1)-dimensional generalized breaking soliton equation was proposed in the form[1]

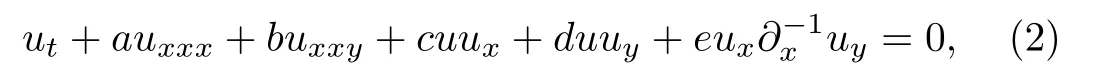
wherea,b,c,d,andeare real parameters.Equation(2)includes a lot of nonlinear evolution equations as its special cases.[1]For example,ifu=wx,a=c=0,b=1,d=−4,e=−2,then this equation reduces to the standard breaking soliton equation(1).Other nonlinear equations can be obtained for speci fic values of the parameters as shown in Ref.[1].In Ref.[1],and by using the singularity analysis and the Bell polynomials-approach,the integrability of the generalized breaking soliton equation(2)was examined.It was shown that this equation passes the Painlev´e test for the special cases of the parameters

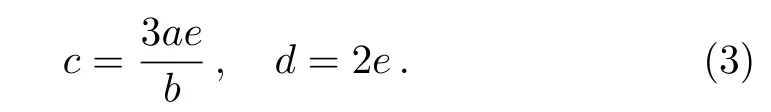
This in turn gives a new(2+1)-dimensional generalized integrable breaking soliton equation

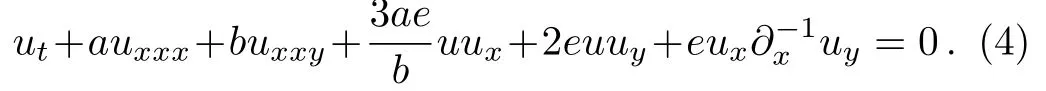
The bilinear B¨acklund transformation,Lax pair and in finite conservation laws for Eq.(4)are derived with the binary Bell polynomials in Ref.[1].

In this work,our main focus will be on studying the new(2+1)-dimensional generalized integrable breaking soliton equation(4).The main concern will be on the derivation of multiple soliton solutions,by using the simplified Hirota method.Moreover,we will derive traveling wave solutions and periodic solutions by using a variety of solitary wave ansatze.This new equation is rich of many kinds of solutions.

2 New Integrable(2+1)-Dimensional Generalized Breaking Soliton Equation

In this section we will apply the simplified form of the Hirota bilinear method[4−5]to study the(2+1)-dimensional breaking soliton equation(4)given earlier.

To remove the integral operator we use the potential

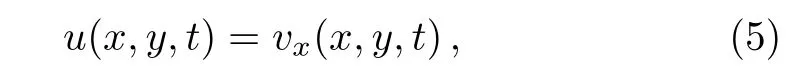
which will carry(4)to the equation

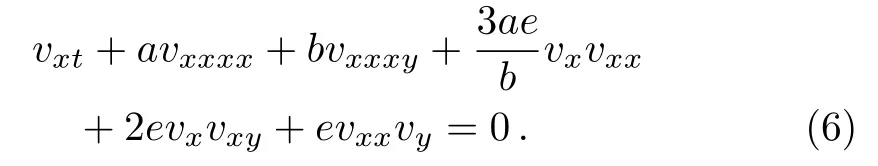
To determine the dispersion relation we substitute

into the linear terms of Eq.(6),and solving the resulting equation forωigives the dispersion relation as

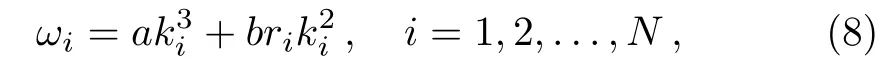
and hence the dispersion variableθibecomes

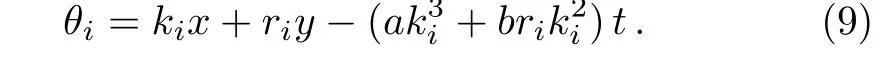
We next use the transformation

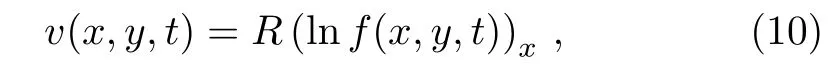
where the auxiliary functionf(x,y,t)is defined by

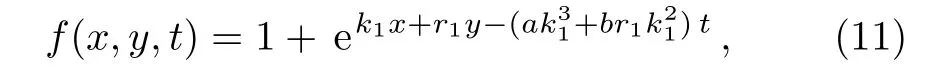
into Eq.(6)and solve to find that

Substituting Eqs.(11)and(12)into Eq.(10)gives the single soliton solution

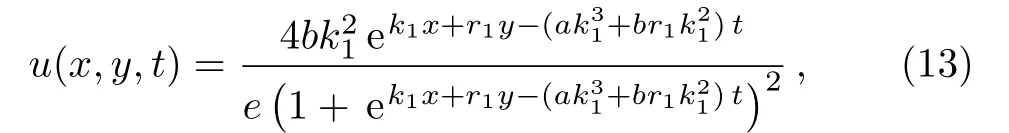
obtained upon using the potential(5)defined earlier.

For the two-soliton solutions,we use the auxiliary functionf(x,y,t)as

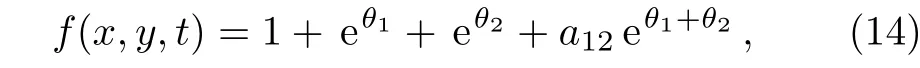
whereθ1andθ2are given above in Eq.(9),and by using Eq.(10)in Eq.(6)to obtain the phase shifta12as

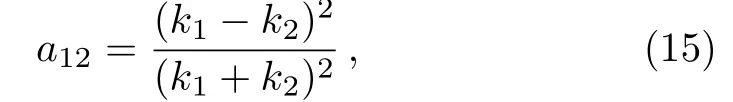
and this can be generalized for the phase shifts in general by

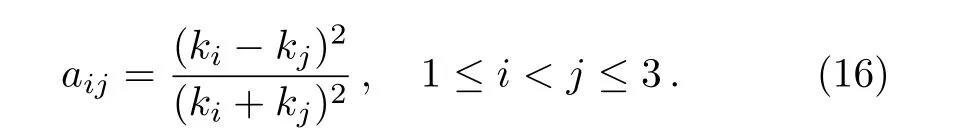
The auxiliary functionf(x,y,t)for the two-soliton solutions thus reads

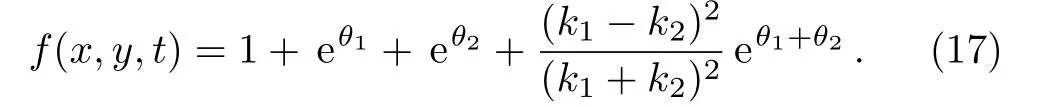
To determine the two-soliton solutions explicitly,we substitute Eq.(17)into Eq.(10).

To determine the three-soliton solutions,we use the auxiliary function

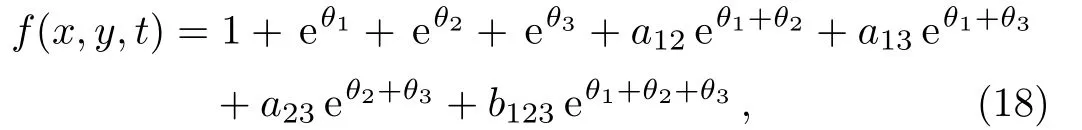
and by proceeding as before to find that

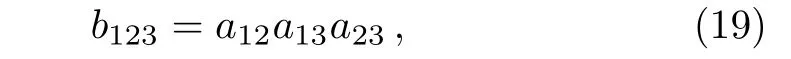
where the phase shiftsaijare defined in Eq.(16).To determine the three-soliton solutions explicitly,we substitute the last result forf(x,y,t)into Eq.(10).

3 Traveling Wave and Periodic Solutions

In this section we will employ a variety of solitary waves ansatze to determine solitonic,singular and periodic solutions for the new integrable(2+1)-dimensional generalized breaking soliton equation(6).

3.1 Using the tanh Method

Using the tanh method,we assume that the solution takes the form

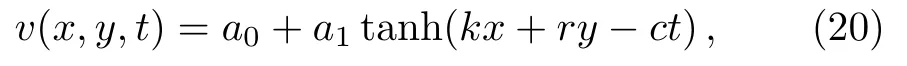
wherea0anda1are constants to be determined,andcis the dispersion relation.Substituting Eq.(20)into Eq.(6),and solving the results we find

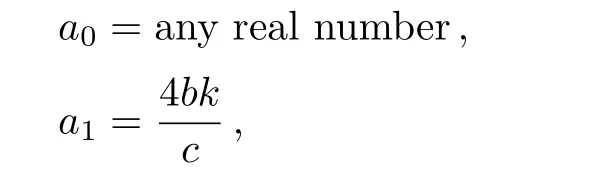
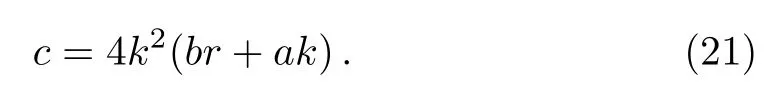
This in turn gives the front wave solution

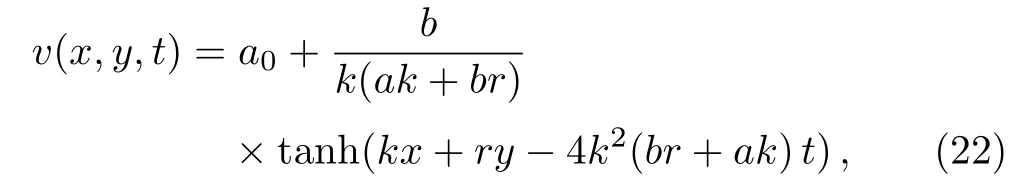
and by using the potentialu(x,y,t)=vx(x,y,t),we obtain the soliton solution

Notice that the amplitude and the wave speed of the obtained soliton in Eq.(23)are given as

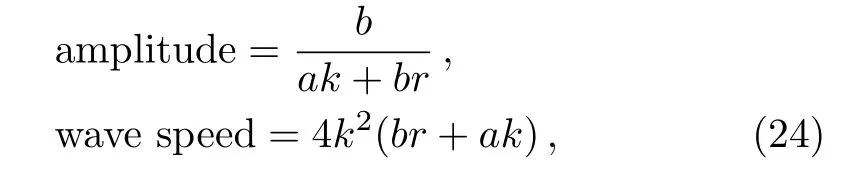
respectively,where each depends ona,b,k,andr.

However,in a like manner we can show that

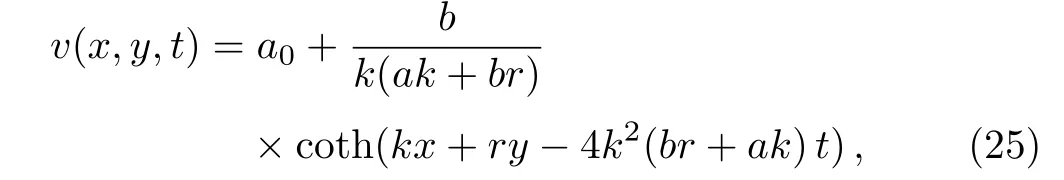
and by using the potentialu(x,y,t)=vx(x,y,t),we obtain the singular soliton solution

3.2 Using the tan Method

To determine periodic solutions,we use the tan method in the form

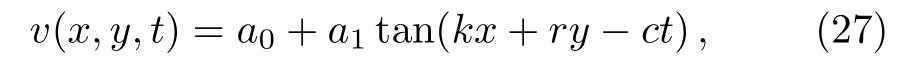
wherea0anda1are constants to be determined,andcis the dispersion relation.Substituting Eq.(24)into Eq.(6),and solving the results we find

This in turn gives the periodic solution

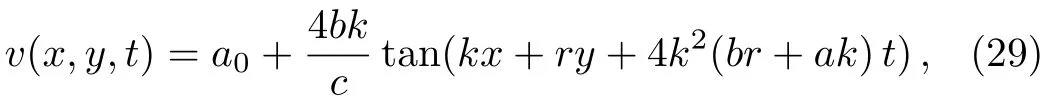
where by using the potentialu(x,y,t)=vx(x,y,t),we find the periodic solution

However,in a like manner we can show that

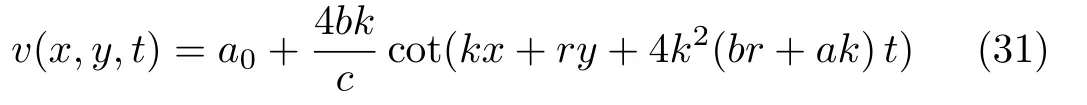
is a singular solution for Eq.(6),andu(x,y,t)can be obtianed noting thatu(x,y,t)=vx(x,y,t).

3.3 Other Solutions

To determine other solutions,we assume that the solution takes the form

wherea0anda1are constants to be determined,andcis the dispersion relation.Substituting Eq.(32)into Eq.(6),and solving the results we find

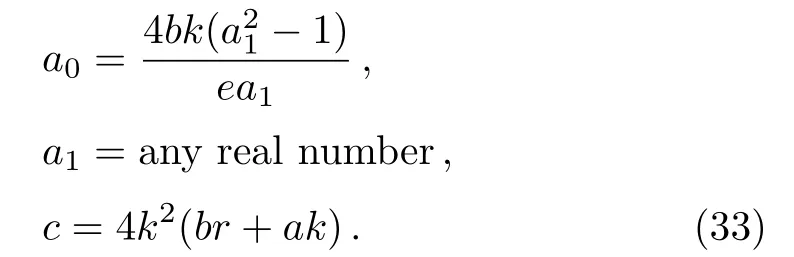
This in turn gives the front wave solution

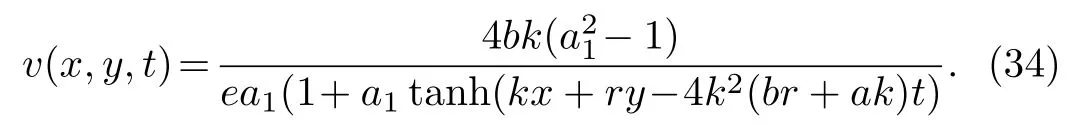
However,in a like manner we can also determine the singular solution

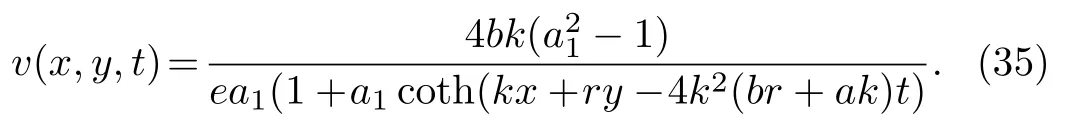
Moreover,following the analysis presented earlier,we can derive the following traveling wave solutions

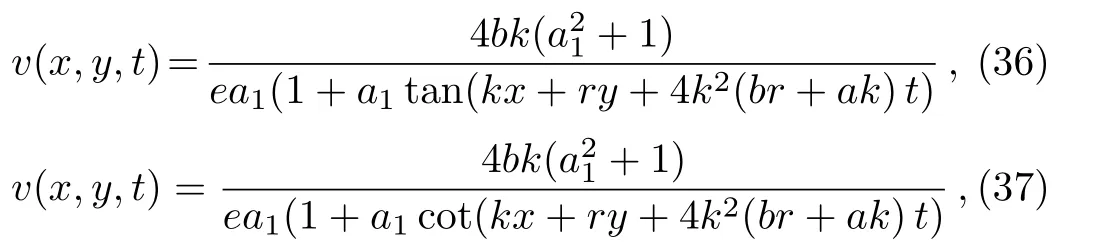
wherea1is left as a free parameter.

4 Discussion

In this work we studied the new(2+1)-dimensional generalized breaking soliton equations.Multiple soliton solutions were formally derived by using the simplified Hirota method.A variety of traveling wave and periodic solutions were also derived by using the tanh-coth method and solitary wave ansatze.

References

[1]G.Q.Xu,Appl.Math.Lett.50(2015)16.

[2]S.H.Ma,J.Peng,and C.Zhang,Chaos,Solitons&Fractals46(2009)210.

[3]Y.T.Gao and B.Tian,Comput.Math.Applic.12(1995)97.

[4]R.Hirota,The Direct Method in Soliton Theory,Cambridge University Press,Cambridge(2004).

[5]W.Hereman and A.Nuseir,Mathematics and Computers in Simulation43(1997)13.

[6]W.Mal fliet,J.Comput.Appl.Math.164-165(2004)529.

[7]W.Mal fliet,Am.J.Phys.60(1992)650.

[8]W.Mal fliet and Willy Hereman,Phys.Scr.54(1996)563.

[9]Xu You-Sheng,Wu Feng-Min,and Lin Ji,Chin.Phys.B12(2003)1049.

[10]A.M.Wazwaz and G.Q.Xu,Commun.Theor.Phys.63(2015)727.

[11]H.Leblond and D.Mihalache,Phys.Rep.523(2013)61.

[12]H.Leblond and D.Mihalache,Phys.Rev.A79(2009)063835.

[13]A.M.Wazwaz,Partial Differential Equations and Solitary Waves Theorem,Springer and HEP,Berlin(2009).

[14]A.M.Wazwaz,Phys.Scr.82(2010)82065006.

[15]A.M.Wazwaz,Phys.Scr.83(2011)035003.

[16]A.M.Wazwaz,Appl.Math.Comput.150(2004)365.

[17]A.M.Wazwaz,Appl.Math.Comput.188(2007)1205.

[18]A.M.Wazwaz,Gaussian Solitary Wave Solutions for Nonlinear Evolution Equations with Logarithmic Nonlinearities,Nonlinear Dynamics,DOI 10.1007/s11071-015-2349-x(2015).

[19]A.M.WazwazandS.A.El-Tantawy,ANewIntegrable(3+1)-DimensionalKdV-LikeModelwithIts Multiple-Soliton Solutions,Nonlinear Dynamics,DOI 10.1007/s11071-015-2427-0(2015).

[20]A.M.Wazwaz,Appl.Math.Mode.38(2014)110.

[21]A.M.Wazwaz,Phys.Scr.81(2010)035005.