Darboux Transformation for a Four-Component KdV Equation∗

Nian-Hua Li(李年华)and Li-Hua Wu(吴丽华)

School of Mathematics,Huaqiao University,Quanzhou 362021,China

1 Introduction

Soliton equations have wide applications in wave motion,nonlinear optics,geometry,and many other fields.The celebrated examples involve the Korteweg-de Vries(KdV)equation,the nonlinear Schr¨odinger(NLS)equation and the sine-Gordon equation.Since these,multicomponent generalizations of classical soliton equations have attracted much attention,such as the Hirota-Satsuma,[1−3]the Yajima-Oikawa,[4−5]the Manakov.[6]

Searching for explicit solutions of soliton equations is one of important subject in soliton theory. There exists many methods to find exact solutions,including inverse scattering transformation,algebro-geometric approach,Hirota’s bilinear method,B¨acklund transformation,Darbourx transformation(DT)etc.Among them,DT is a powerful and direct tool to construct the solutions for the integrable systems.[7−9]There are different techniques to derive the DT,for instance,operator decomposition method,[10]gauge transformation,[11−12]loop group method,[13]and Riemann-Hilbert method.[14]

Recently, Geng and Wang[15]derived a fourcomponent KdV equation

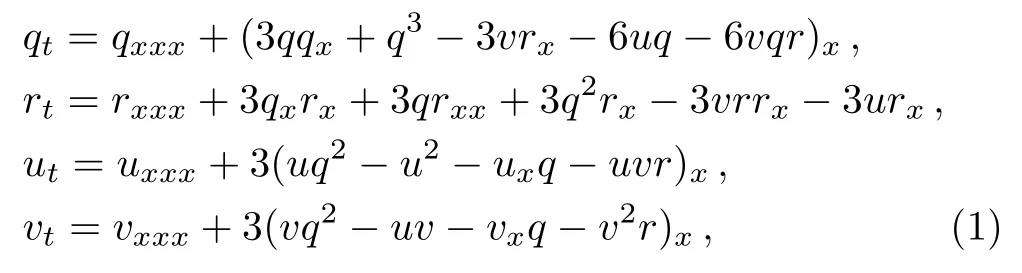
by considering the following Lax representation

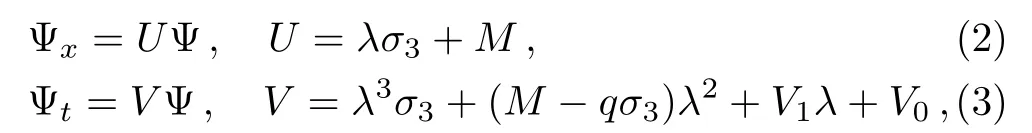
where,σ3=diag(1,0,0),λis a spectral parameter and

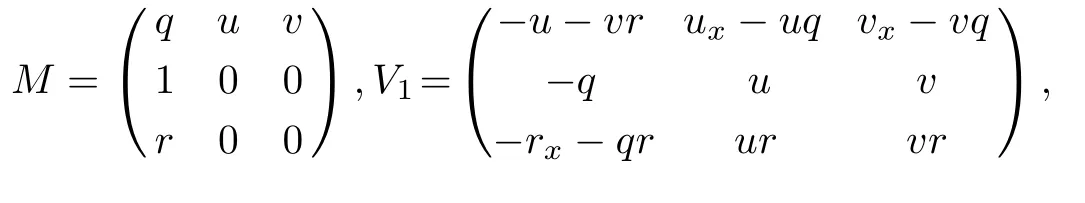
hereinθ=qxx+2qqx−2uq−2qvr−vxr−2vrx−ux,ϑ=q2+qx−2u−2vr.Equation(1)is reduced to the KdV equation asu=v,q=0,r=1.The Hamiltonian structures of Eq.(1)are established using the trace identity.The aim of the present paper is to derive the DT of the four-component KdV equation and obtain some exact solutions applying the DT.

This paper is organized as follows.In Sec.2,we construct a DT for the four-component KdV equation with the aid of a gauge transformation.In Sec.3,we show the N-fold DT of the system by iteration.In Sec.4,applying the DT,we obtain several exact solutions of fourcomponent KdV equation from some trivial seed solutions.

2 A Darboux Transformation

To derive a DT for the four-component KdV Eq.(1),let us start with the spectral problem(2).Lemma 1Letunder the gauge transformation

the 3×3 spectral problem(2)is transformed into

where

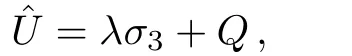
In fact,di ff erentiating(4)with respect tox,we get

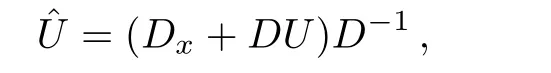
which implies(6).

It is easy to show that the spectral problem(5)is nothing but that of the coupled AKNS hierarchy(see e.g.Refs.[16–17]).Therefore we may establish the DT for the spectral problem(2)using the well-known results for the coupled AKNS hierarchy.As pointed out in Ref.[18],a DT for the coupled AKNS hierarchy is constructed as

by combining the spectral problem(5)and its conjugate problem

whereandare solutions of the spectral problems(5)and(8)with the spectral parametersµ1andν1respectively.Consequently,the construction of the DT for the spectral problem(2)can be depicted by following diagram

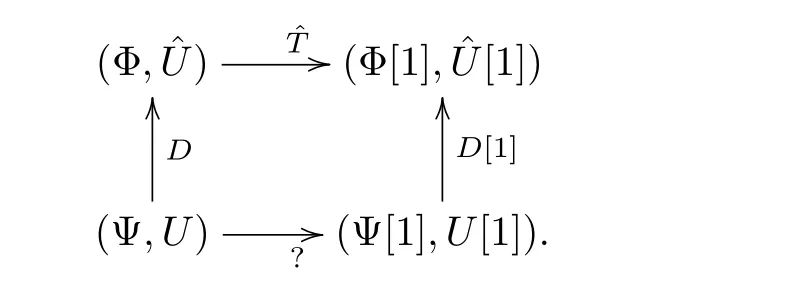
Theorem 1Letandbe solutions of the spectral problem(2)and its conjugate problem

with the spectral parametersµ1andν1respectively.Then we have the transformation formulae for the fields in the four-component KdV equation(1)

where

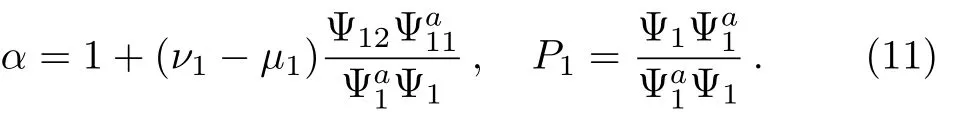
ProofThe DT(7)infers that the matrixshould satisfy

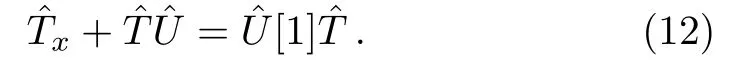
Expandinginto Laurent polynomials of the spectral parameterλat∞and substituting it into(12),we have

It follows from(13)that

Furthermore,noting that the spectral problem(2)is transformed into(5)under the gauge transformation(4),one can easily verify that the adjoint problemis transformed intounder the gauge transformation.Hence the DT for the spectral problem(2)is obtained as

A direct computation shows thatT=diag(α,1,1)(I+[(ν1−µ1)/(λ−ν1)]P1),which satisfies

ExpandingTinto Laurent series ofλat∞in(15)and comparing the coefficients give rise to

which yields the transformation(10).

3 Iterations:N-fold Darboux Transformation

It is well-known that iteration problem for the DT is important in the process of searching for N-solitons and many other solutions,so the construction of the N-fold DT for the spectral problem(2)is necessary.

Firstly,let us consider theN-fold DT for the spectral problem(5).In which the DT matrix is given by[18]

with

where⟩is a special solution for system(5)withλ=µiandis a special solution for the conjugate spectral problem(8)withλ=νi.Then the N-fold DT for the spectral problem(2)can be obtained by following diagram

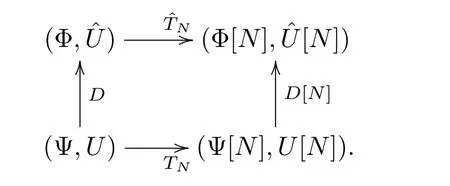
Taking the similarly process in Sec.2,we get

In particular

whereY2is the second row inYandis the first column inYawith

herein|yi⟩andare solutions of the spectral problems(2)and(9)withλ=µiandλ=νirespectively.Then an explicit expression for the DT matrixTNmay be gotten by a directly calculation,that is

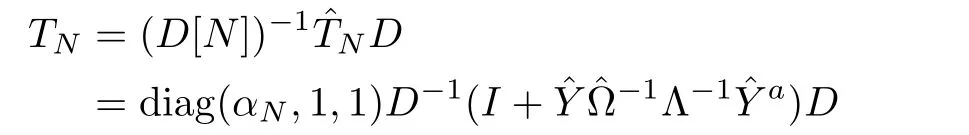
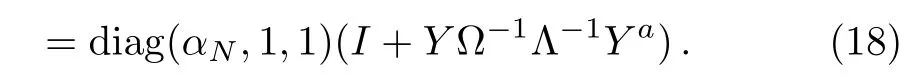
Secondly,it follows the DT that

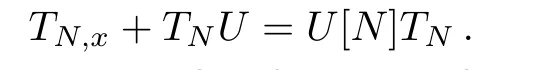
Expanding the equation by the spectral parameterλasλ→∞,we get a transformation for the fields in the system(1),that is

Finally,we will discuss the reduced DT and 2-fold DT for the system(1)withq,r,u,v∈R.In this case we have¯U(¯λ)=U(λ).

(i)When we consider the DT for(16),we havewhich is satisfied as

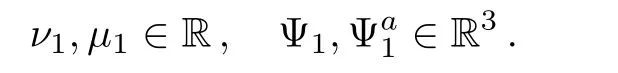
Then a DT for the system(1)is obtained with the DT matrix given by

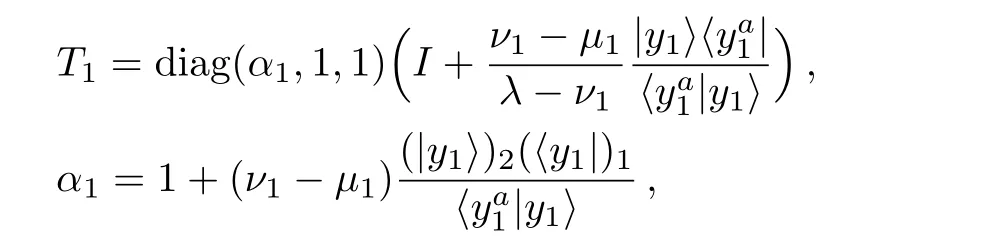
whereν1,µ1∈R and

(ii)When we consider the 2-fold DT,we haveSince

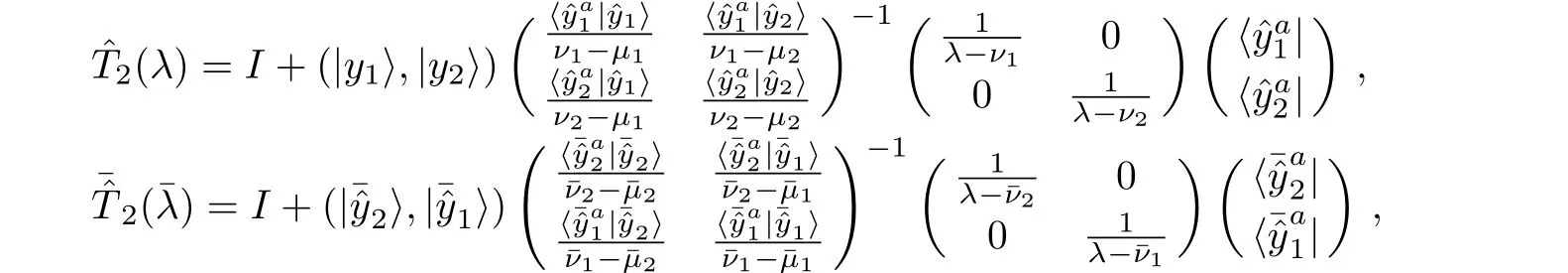
a sufficient condition is obtained as

Therefore we get a 2-fold iterated DT for the system(1),that is

where

4 Solutions of Four-Component KdV System

In this section,we will obtain some explicit solutions of the four-component KdV system(1)by applying the DT(10).

(i)Choosing a trivial solutionu=v=q=r=0 of the four-component KdV equation(1),then the general solutions for the corresponding spectral problem withλ=µ1and conjugate problem withλ=ν1are given respectivelywhich are

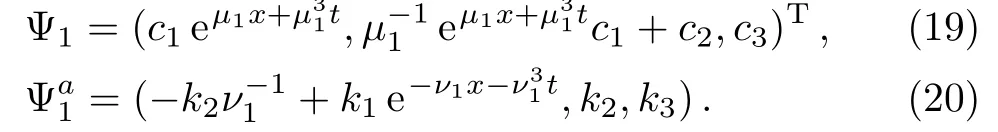
In what follows we will discuss the solutions of the system(1)without singularity in this condition.

Case 1Settingc1=0,k2=0,then the solutions of the spectral problem and the conjugate spectral problem of the four-component system(1)may be chosen as Ψ1=(0,c2,1)Tandand we get a solution of the four-component KdV system

where

Case 2Supposingc1=0,k2=1,the corresponding linear problems can be solved as Ψ1=(0,1,c3)Tandthen a solution is obtained as

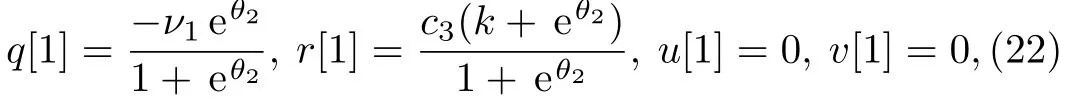
where

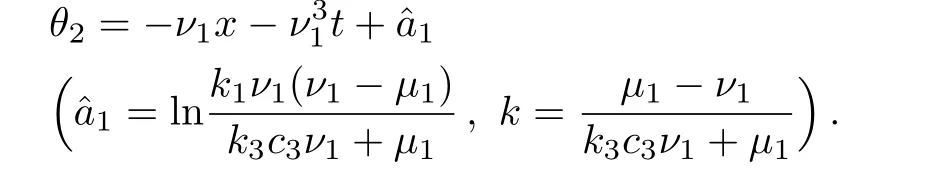
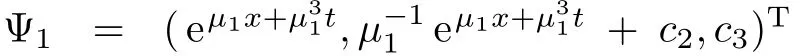
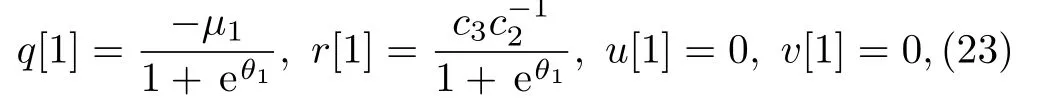
where

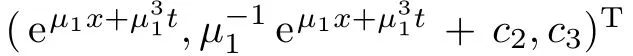
(a)Whenk1=0,taking 1/µ1>1/ν1andk3c3+c2>0,a solution is obtained as

where

(b)Whenif 1/µ1>1/ν1andk3c3+c2>0,then the solutions of the spectral problem and the conjugate spectral problem may be chosen as Ψ1=andand a solution is calculated as

whereA direct computation shows that these solutions are soliton solutions if the parameters are chosen suitably(see Figs.1(a)-1(d)).

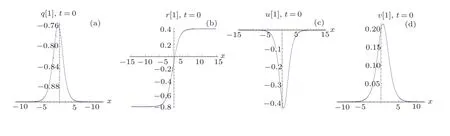
Fig.1 The solution q[1],r[1],u[1],v[1]with µ1=0.9,ν1=1.8,k1=1.0,k3= −0.5,c2=1,c3= −0.8.

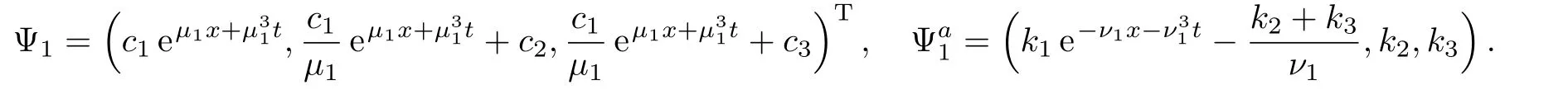
Using the Darboux transformation(10),we get a solution of the four-component KdV Eq.(1)

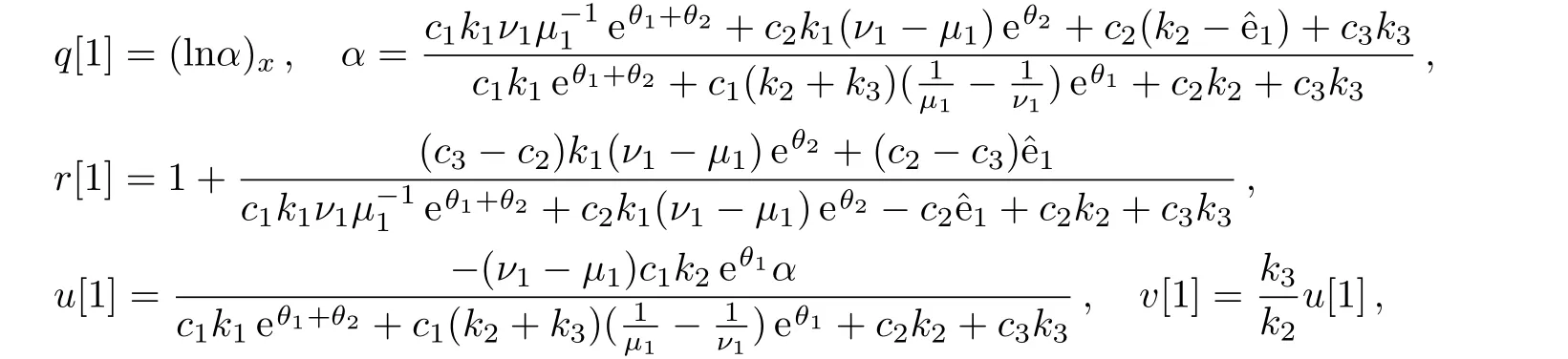
whereThese solutions are soliton solutions if the parameters are chosen suitably(see Figs.2(a)–2(d)).

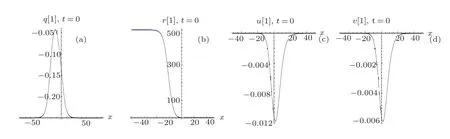
Fig.2 The solution q[1],r[1],u[1],v[1]with µ1=0.25,ν1=0.005,c1=0.05,c2= −0.3,c3= −1,k1=0.5,k2=−0.02,k3=−0.02.

(iii)Choosing a trivial solutionu=q=r=0,v=1 of the four-component KdV Eq.(1),then the corresponding spectral problem withλ=µ1and conjugate problem withλ=ν1are solved as

Using the Darboux transformation(10),we get another solution of the four-component KdV equation(1).

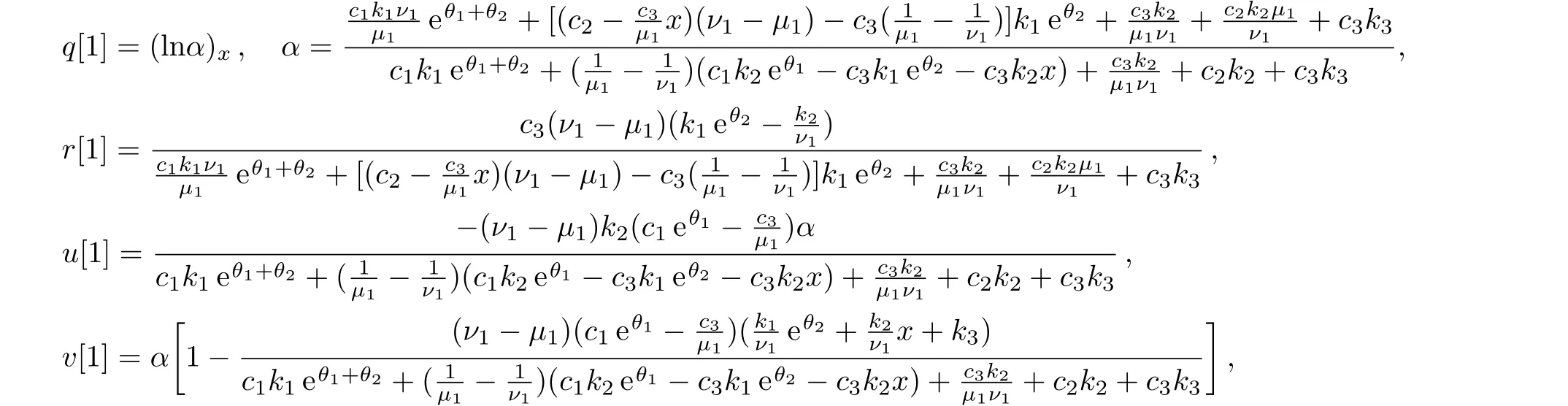
whereThese solutions are soliton solutions if the parameters are chosen suitably(see Figs.3(a)–3(d)).

Fig.3 The solution q[1],r[1],u[1],v[1]with µ1=0.5,ν1=0.001,c1=5,c2=2,c3=0.1,k1=15,k2= −0.01,k3= −0.01.

It is remarkable that the singularity in(ii)and(iii)may be also considered but not given here.

References

[1]R.Hirota and J.Satsuma,Phys.Lett.A85(1981)407.

[2]Y.T.Wu,X.G.Geng,X.B.Hu,and S.M.Zhu,Phys.Lett.A255(1999)259.

[3]M.G¨urses,A.Karasu,and V.V.Sokolov,J.Math.Phys.40(1999)6473.

[4]N.Yajima and M.Oikawa,Prog.Theor.Phys.56(1976)1719.

[5]J.L.Zhang and M.L.Wang,Commun.Theor.Phys.42(2004)491.

[6]S.V.Manakov,Sov.Phys.JETP38(1974)248.

[7]X.Wang and Y.Chen,Commun.Theor.Phys.61(2014)423.

[8]Q.Chen,W.G.Zhang,H.Q.Zhang,and B.Yang,Commun.Theor.Phys.62(2014)373.

[9]W.Liu,D.Q.Qiu,and J.S.He,Commun.Theor.Phys.63(2015)525.

[10]P.Deift and E.Trubowitz,Commun.Pure Appl.Math.32(1979)121.

[11]V.B.Matveev and M.A.Salle,Darboux Transformations and Solitons,Springer,Berlin(1991).

[12]C.H.Gu,H.S.Hu,and Z.X.Zhou,Darboux Transformations in Integrable Systems:Theory and Their Applications to Geometry,Springer,Dordrecht(2005).

[13]C.L.Terng and K.Uhlenbeck,Commun.Pure Appl.Math.53(2000)1.

[14]S.P.Novikov,S.V.Manakov,V.E.Zakharov,and L.P.Pitaevskii,Theory of Solitons:The Inverse Scattering Method,Springer,New York(1984).

[15]X.G.Geng and H.Wang,Chin.Phys.Lett.31(2014)070202.

[16]M.J.Ablowitz,D.J.Kaup,A.C.Newell,and H.Segur,Phys.Rev.Lett.31(1973)125.

[17]Q.P.Liu,J.Math.Phys.37(1996)2307.

[18]D.F.Bian,B.L.Guo,and L.M.Ling,Stud.Appl.Math.134(2015)181.