On Integrals Involving Universal Associated Legendre Polynomials and Powers of the Factor(1 −x2)and Their Byproducts∗

2016-05-10DongShengSun孙东升YuanYou尤源FaLinLu陆法林ChangYuanChen陈昌远andShiHaiDong董世海

Communications in Theoretical Physics 2016年10期

关键词：东升

Dong-Sheng Sun(孙东升), Yuan You(尤源),Fa-Lin Lu(陆法林),Chang-Yuan Chen(陈昌远), and Shi-Hai Dong(董世海)

1School of New Energy and Electronics,Yancheng Teachers University,Yancheng 224002,China

2CIDETEC,Instituto Polit´ecnico Nacional,Adolfo Lpez Mateos,CDMX,C.P.07700,Mexico

1 Introduction

As we know,the associated Legendre polynomials play an important role in the central fields when one solves the physical problems in the spherical coordinates.Nevertheless,in the case of the non-central field we have to introduce the universal associated Legendre polynomialswhen studying the modified Pschl–Teller[1−3]and the single ring-shaped potential,[4−12]in which the quantum numbersl′andm′are not integer,but their differencel′−m′=nis integer.Its series expression is

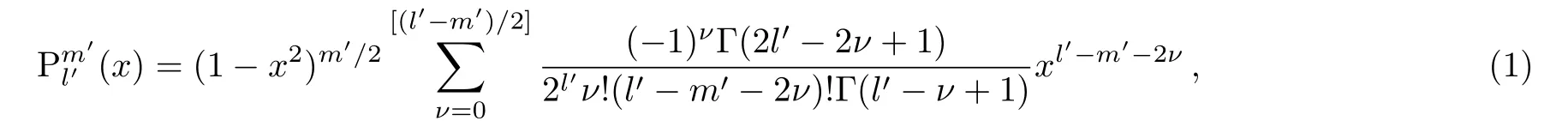
whose properties have been studied in Refs.[1,3,13].For example,using one of its properties

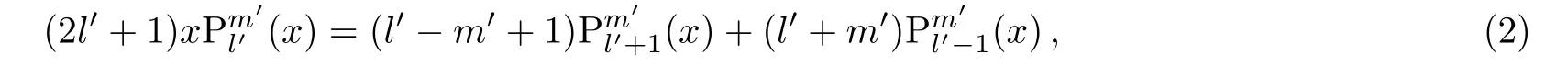
as well as its normalization relations,we have obtained an important result which is unavailable in popular textbooks and handbooks in Ref.[14]

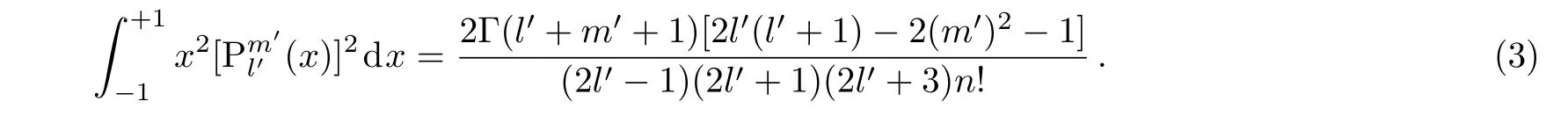
Other relevant important integrals have also been obtained since they are unavailable in classic handbooks.[15−16]In our recent study,[17]we have obtained some important integrals,so as

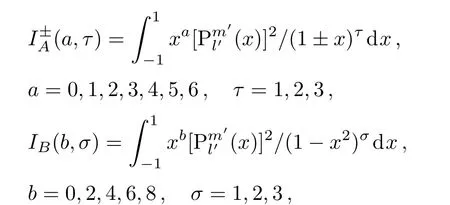
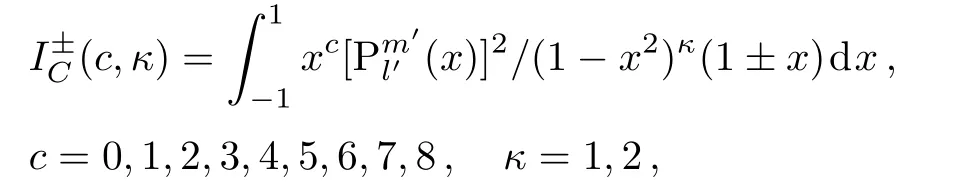
which are unavailable in classic handbooks.We find that all of these integrals depend on the integrals

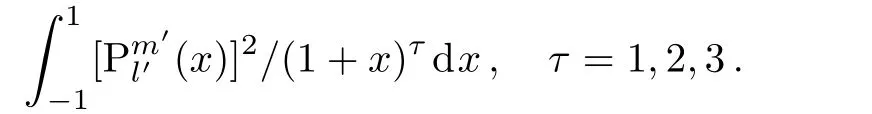
However,when the parameters are taken as arbitrary positive real numbers,the integrals become rather difficult to evaluate.

In this work,our main aim is to attack this problem.

That is,the integrals to be calculated are defined as

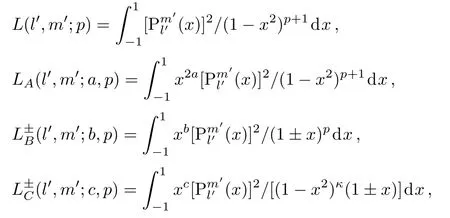
respectively.The parameters a,b,c,p and κ are arbitrary positive real numbers.It should be noted that all de finite integrals presented here for integer quantum numbers l′and m′inare also useful since they are unavailable in classical handbooks of integrals.

The rest of this work is organized as follows. In Sec.2 we derive the de finite integrals L(l′,m′;p)and.The de finite integralsandare derived in Secs.3 and 4,respectively.Some concluding remarks are given in Sec.5.

2 De finite Integrals L(l′,m′;p)andLA(l′,m′;a,p)

To solve this problem,let us begin by considering the relation between theand the hypergeometric functions[13]

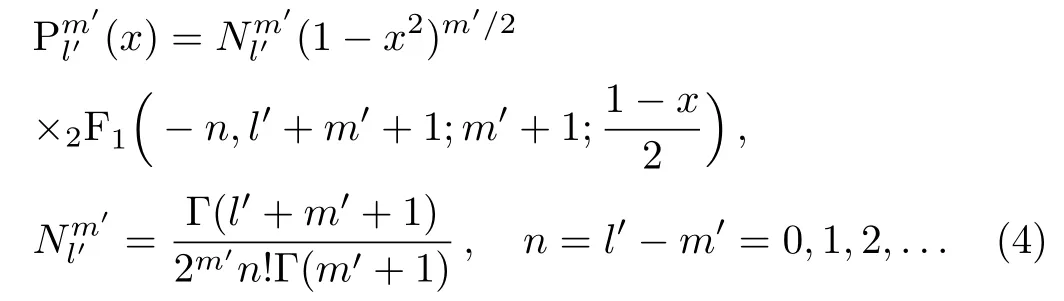
Now,let us first study the integral

which is helpful in deriving other integrals.

Using important identities for the hypergeometric series Refs.[15,18],i.e.,

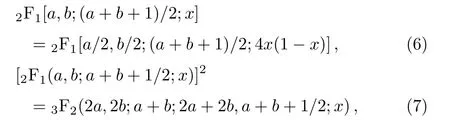
we have

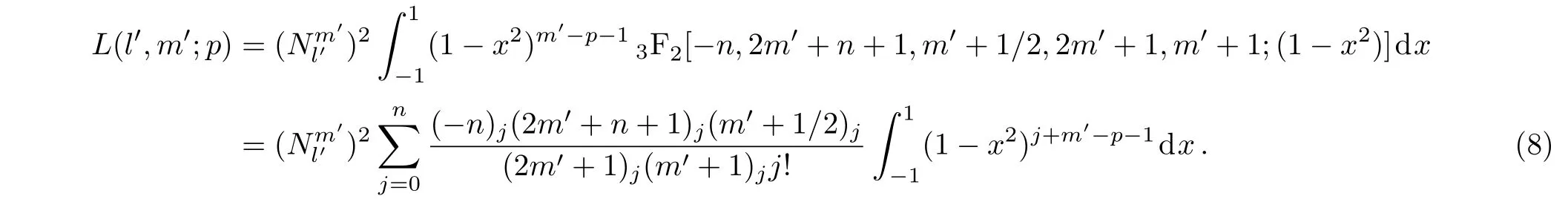
According to the definition of the beta function

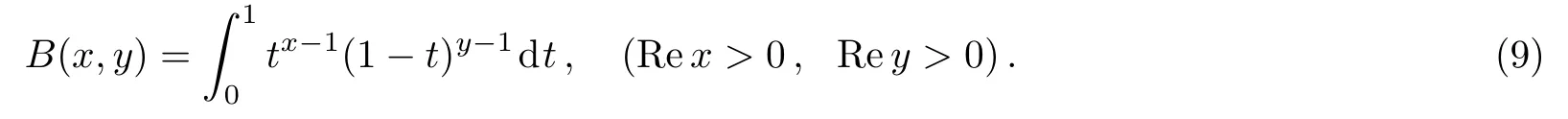
Take a new variable ν=2t− 1,the above beta function is modified as

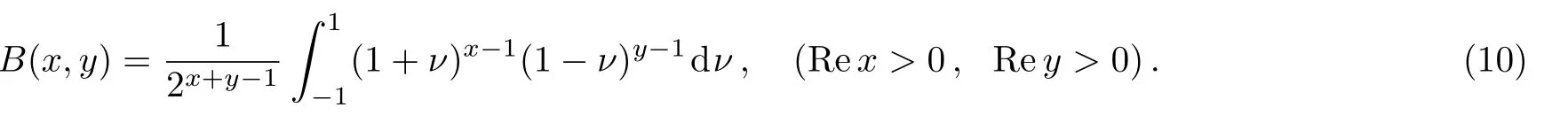
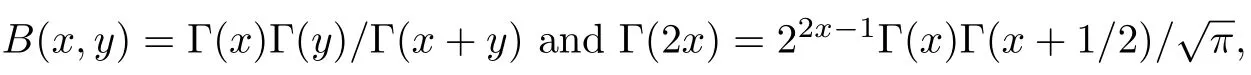
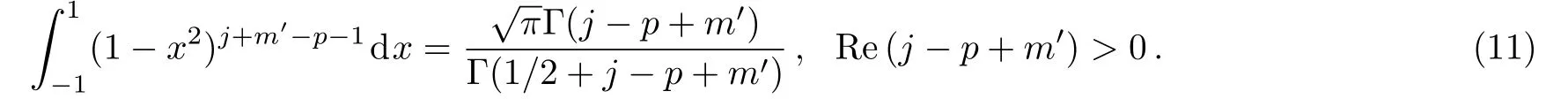
Thus,the integral(8)can be simplified as

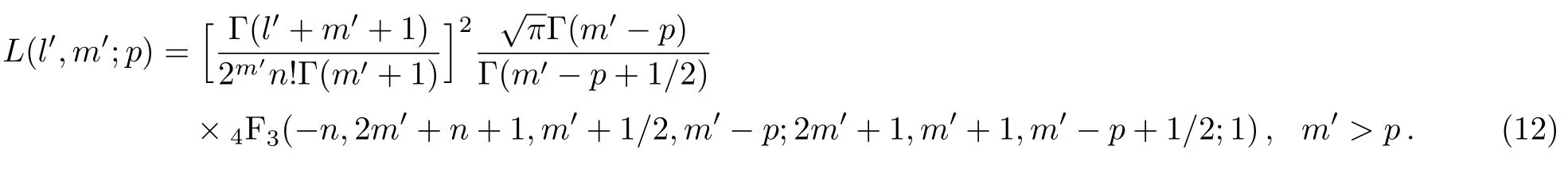
Now,we give the results for some special cases n=l′− m′=0,p=0,and p= −1.

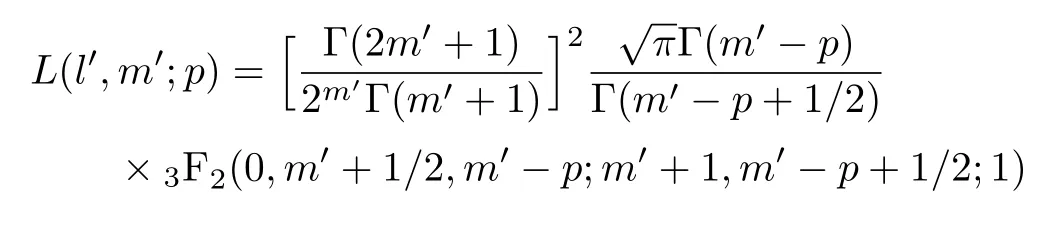
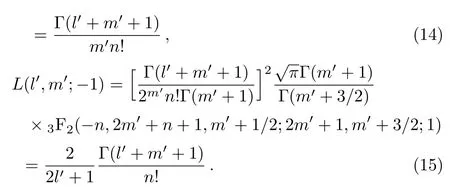
We find that some of these special results are essentially same as those given in Refs.[17,19–22]when l′and m′are taken integers.

Let us study the following integral based on the result(12)

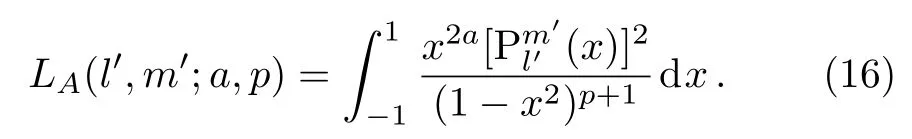
Similarly if we define t=s2in Eq.(9),then the beta function can be rewritten as

Using this and also the relation between the beta function and the Gamma function,we obtain the following integral

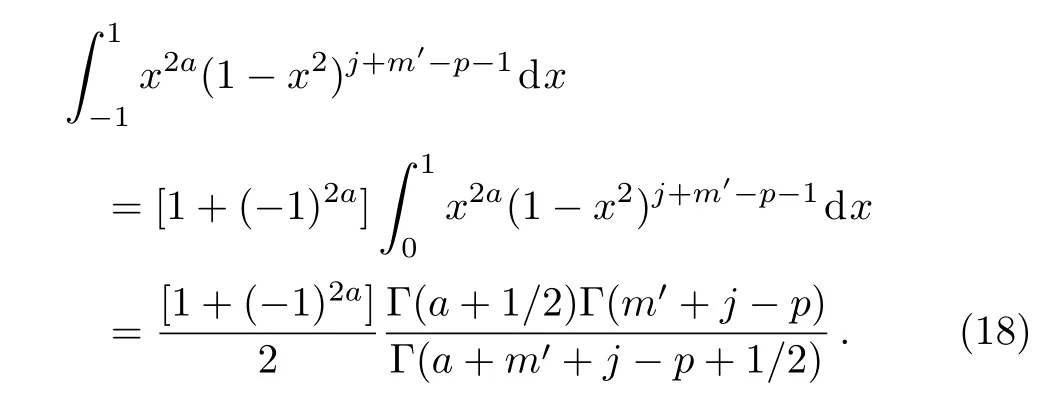
Thus,the integral(16)can be simplified as

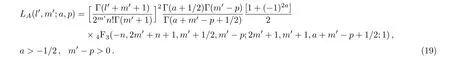
3 De finite Integral

Let us study another type of integral in terms of the result(8)

which can be rewritten as

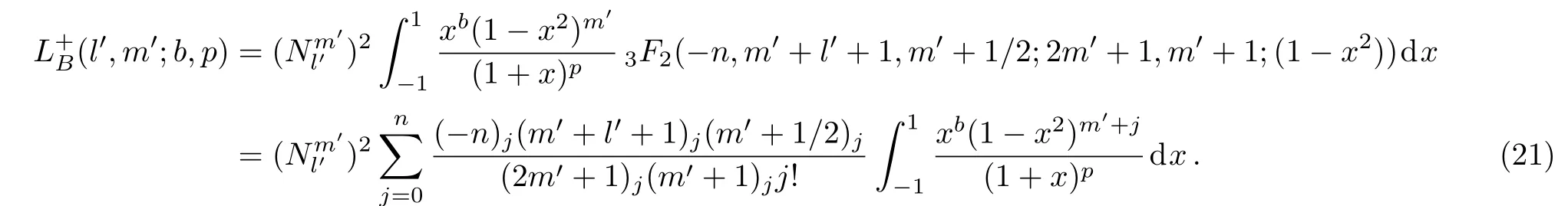
Making use of the following relation[15,18]

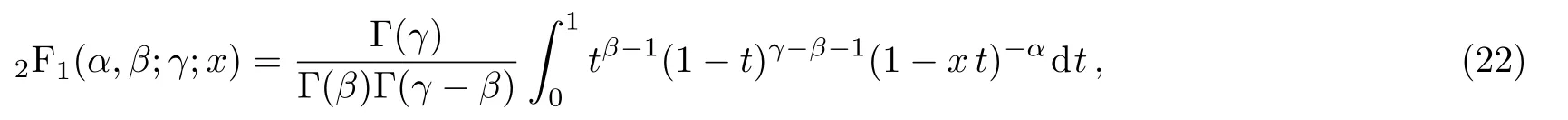
the integral in Eq.(21)can be evaluated as

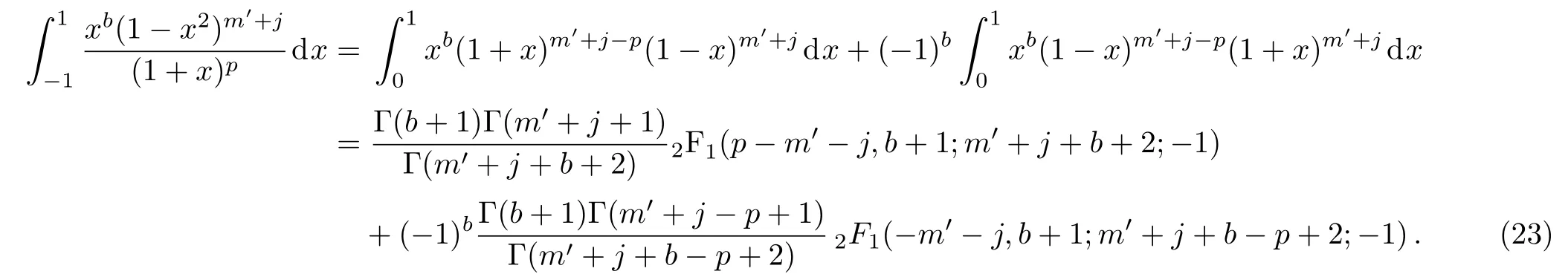
Obviously,the value of parameter b determines the final result of this integral.Substitution of this into Eq.(21)yields

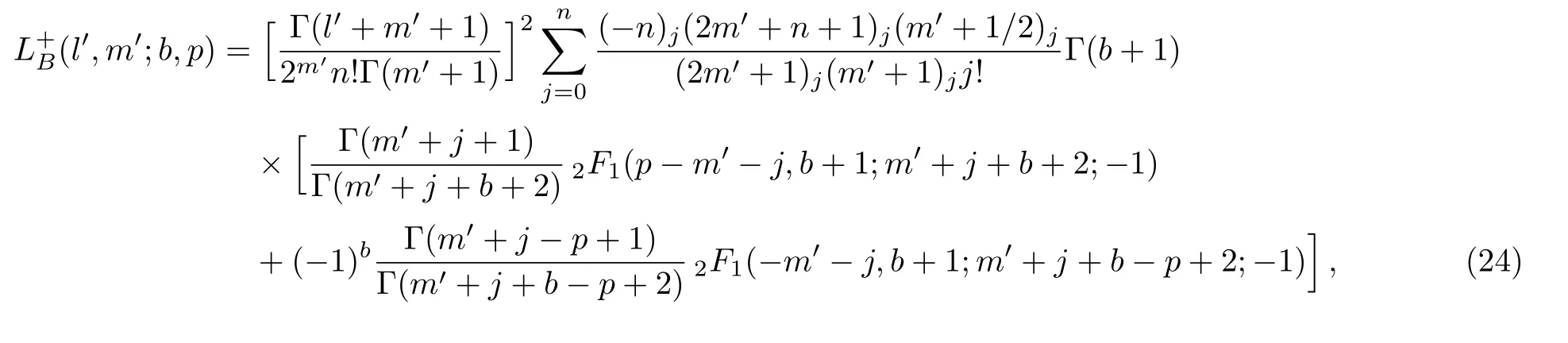
where b>−1,m′−p>0.

Moreover,based on the beta function,we have

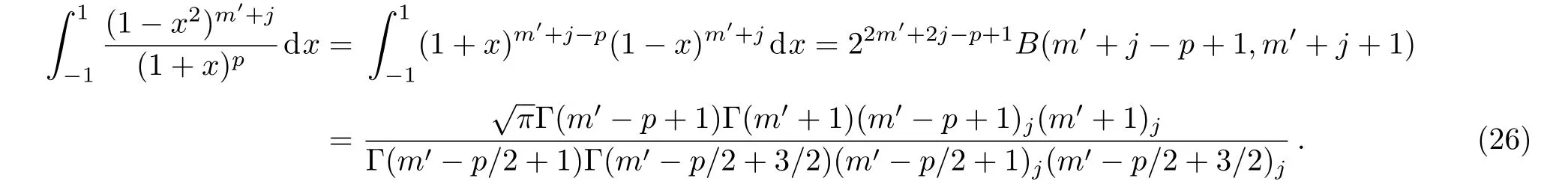
In addition,for b=0 Eq.(24)is simplified as

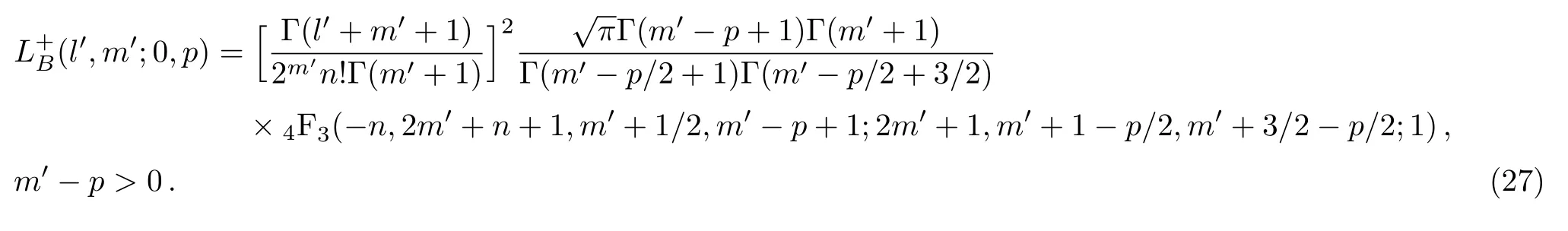
4 De finite Integral

Finally,we are going to study the third integral

Likewise,the integralcorresponding to the integral involving the factor 1/(1−x)has the property

5 Concluding Remarks

We have calculated an important integral

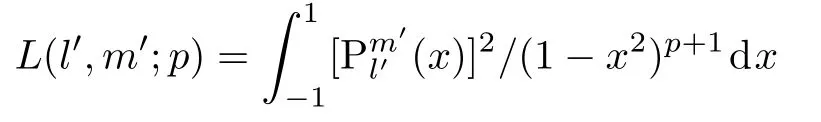
using the basic properties of the generalized hypergeometric function4F3(a,b,c,d;e,f,g;1)and then systematically obtained other interesting integrals LA(l′,m′;a,p),andgiven in Eqs.(19),(24),and(29),respectively.The integralsandcan be derived easily by parity. What have we done is the generalization of our previous results for the integrals whose parameters are taken as natural numbers[17]to those for arbitrary real numbers.Such results will be more useful and helpful in practice problems.It should be emphasized that these integrals cannot be found in the popular integral handbooks.The results presented here are interesting both in mathematics itself and in theoretical physics.On the other hand,the results for integers m′and l′are also important since all of them are unavailable in popular handbooks besides they are useful in calculating the matrix elements in spin-orbit interactions and other relevant problems.