一种新型的基于Hadoop框架的分布式并行FP－Growth算法

张振友，孙 燕，丁铁凡，刘鹏飞

（华北理工大学信息工程学院，河北唐山 063009）



一种新型的基于Hadoop框架的分布式并行FP－Growth算法

张振友，孙 燕，丁铁凡，刘鹏飞

（华北理工大学信息工程学院，河北唐山 063009）

摘 要：针对传统FP－Growth算法在大规模数据环境下存在的挖掘效率低和内存溢出问题，在传统FP－Growth算法的基础上，提出一种新的并行FP－Growth算法，并在分布式计算框架Hadoop 的MapReduce编程模式下实现并行化处理。实验数据表明，并行的FP－Growth算法与传统的FPGrowth算法相比，具有相同数据量下计算时间短，相同时间内处理数据量增大的优点，并在一定条件下解决了大数据挖掘的内存溢出问题。

关键词：并行处理；分布式；数据挖掘；闭频繁项集；Hadoop；FP－Growth

E－mail：youzhenadd＠163．com

张振友，孙 燕，丁铁凡，等．一种新型的基于Hadoop框架的分布式并行FP－Growth算法［J］．河北工业科技，2016，33（2）：169－177．

ZHANG Zhenyou，SUN Yan，DING Tiefan，et al．A novel distributed parallel FP－Growth algorithm based on Hadoop framework［J］．Hebei Journal of Industrial Science and Technology，2016，33（2）：169－177．

关联规则挖掘的基本算法主要有Apriori算法和FP－Growth算法。1993年，AGRAWAL等在美国IBM Almaden Research Center首先提出了关联规则的概念，用于挖掘顾客交易数据库中的频繁模式。至此，诸多的研究人员对关联规则的挖掘问题进行了大量的研究［1］。AGRAWAL提出了经典的Apriori算法来挖掘数据集中的频繁模式，从而挖掘出数据项集之间的关联规则。为了更好地提高挖掘效率，研究人员提出了基于Hash表的项集计数技术（利用Hash表提高项集计数效率），基于事务压缩的算法（压缩进一步迭代扫描的事务数），基于分区的算法（对原始数据进行划分各找候选项集），基于事务抽样技术的算法（关联挖掘在数据样本上而不是整个数据集上进行）以及动态项集计数的算法（在扫描的不同点添加候选项集）等的改进算法［2］。但是这些算法都需要反复地扫描数据库，并且产生大量候选项集，这些缺点会增大系统的开销［3］。于是出现了挖掘全部频繁项集却不产生大量候选项集的频繁模式增长，即FP－Growth（Frequent Pattern－Growth）算法［4－5］。

随着大数据时代的到来，大规模数据的产生从存储和计算两方面考验了单机处理能力，而在处理海量数据时单机环境已远远不能满足。因此，并行计算环境成为了研究者们的新问题。有研究者提出的基于多线程的并行算法，在很大程度上缓解了存储及计算的压力，但是内存资源的局限性成为了算法扩展的瓶颈［6］；有研究人员在MPI并行环境的基础上，使用进程间通信的方式协调并行计算，结果计算效率较低，内存开销大，并且不能够实现多节点的横向扩展［7－8］；为了在某种程度上降低并行计算时的通信消耗，邹翔等［9］提出了一种基于前缀树的并行算法。

针对海量数据的数据挖掘问题，本文提出了一种改进FP－Growth算法。通过分布式计算框架Hadoop的MapReduce编程模式对改进FPGrowth算法的各个步骤并行化［10］，不仅提高了挖掘效率，而且有效地解决了内存不足的问题，并针对算法在挖掘FP－Tree中产生大量的频繁项集的问题，提出了在挖掘过程中发现闭项集就对搜索空间进行剪枝的方法。

1 FP－Growth算法

Apriori算法是关联规则模式挖掘的经典算法，其寻找最大项集的基本思想是：算法需要进行多个步骤处理数据集。第1步，简单统计所有含有1个元素的项集出现的频率，并找出不小于最小支持度的项集。第2步，开始数据处理直到再没有最大项集生成［11－13］。Apriori算法在数据量较小的情况下能够大大压缩候选闭频繁项集的大小，但是由于它需要反复访问事务数据库，并且在对长模式挖掘时会产生大量的候选项集。针对Apriori算法的I／O频繁访问和存储空间大的主要性能瓶颈，提出了FP－Growth算法来减少全量扫描事务数据库的次数，并且不产生候选项集［14－15］。FP－Growth算法使用了一种称为频繁模式树FP－Tree的数据结构，并直接从该结构中提取频繁项集。FP－Tree是一种特殊的前缀树，由频繁项头表和项前缀树构成［16－17］。所谓前缀树，是一种存储候选项集的数据结构，树的分支用项名标志，树的节点存储后缀项，路径表示项集［18］。

假设I＝｛I1，I2，…，Im｝是项的集合。给定一个订单数据库ORDER，其中每个事务R是P的非空子集，即，每一个订单都与一个唯一的标志符RID相对应，如表1所示。

表1　事务数据表Tab．1 Transaction data table

FP－Growth算法的具体步骤［19］如下。

1）第1次全量扫描事务数据库，统计导出k＝1项集以及对应的支持度计数，并且按照支持度计算降序排序，结果记为L。支持度设置为2，则L＝｛｛P2：7｝，｛P1：6｝，｛P3：6｝，｛P4：2｝，｛P5：2｝｝。

2）再次全量扫描事务数据库，按照每个事物中出现的频繁项建立FP－Tree。首先创建树的根节点，记为root。处理每条事务数据按照L频繁项集添加到FP－Tree中的一个分支。

①扫描订单R100的事务“P1，P2，P5”，按照L中的顺序将该事务进行排序为“P2，P1，P5”，构造FP－Tree的第1个分支，如图1所示。

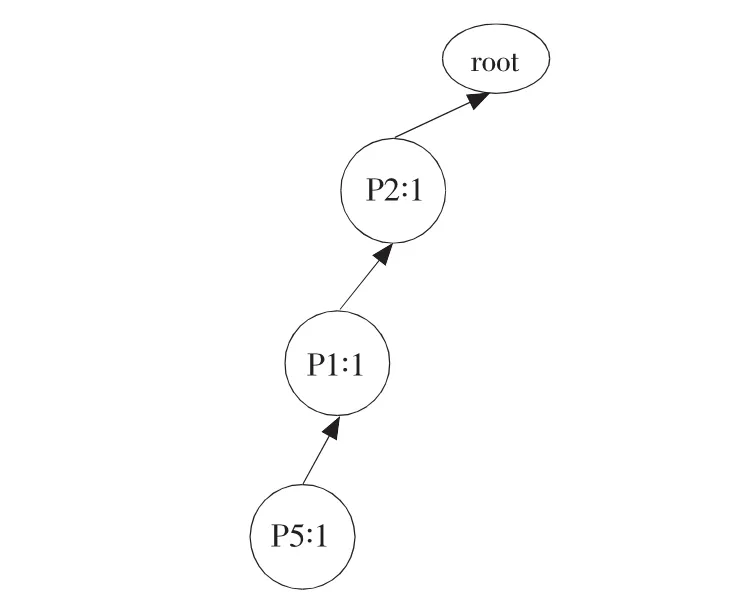
图1　事务R100数据形成的FP－TreeFig．1 FP－Tree built from R100transaction data

②扫描订单R200“P2，P4”，排序为“P2，P4”，与R100共享节点｛P2｝，因此将树中节点｛P2｝的计数加1，同时在｛P2｝节点上创建一个｛P4：1｝的分支，如图2所示。

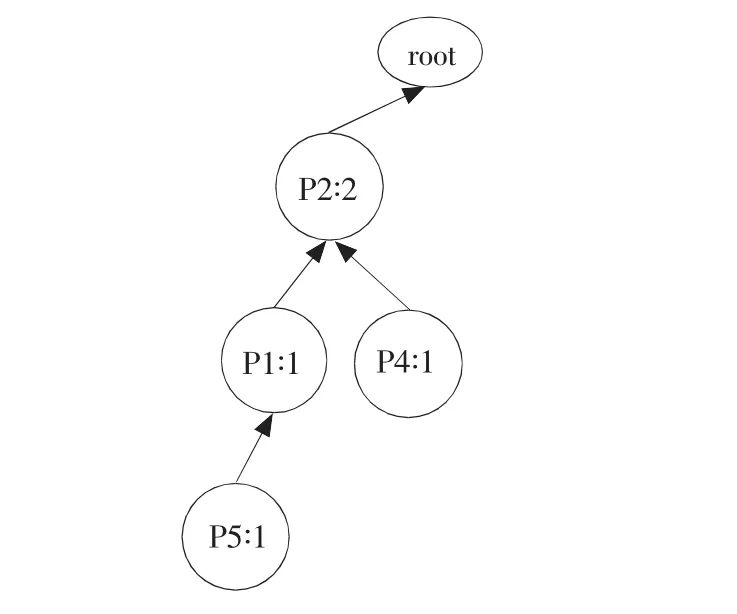
图2　事务R200数据形成的FP－TreeFig．2 FP－Tree built from R200transaction data

③以此类推，将事务数据库中的所有订单都添加到FP－Tree中。

如此，遍历整个事务数据库，每条订单数据排序，创建对应的路径，但是，如果创建路径时遇到相同的节点，该节点计数就增加1。为了使形成的FP－Tree能够方便被遍历，创建一个项头表，表的字段项为ID、支持度计数、节点链。所以，经过上述建立FP－Tree的过程，最终FP－Tree结构如图3所示。

图3　存储频繁模式信息的FP－TreeFig．3 FP－Tree of store frequent patterns information

FP－Growth算法最后一步为挖掘FP－Tree。挖掘过程如下：遍历L频繁项集，构建每个项的条件模式基（即子数据库），通过它的前缀路径来构建条件FP－Tree树，根据项头表至底向上递归挖掘，链接后缀模式与条件FP－Tree生成的频繁模式为最终的频繁项集。表2为FP－Tree挖掘过程的总结。

表2　FP－Tree挖掘过程Tab．2 FP－Tree mining process

综上所述，FP－Growth算法主要分为建立FPTree和挖掘FP－Tree，从而在不产生候选项集的条件下实现频繁项集的挖掘。同时，把数据压缩成树形结构，大大减少了存储空间。传统FP－Growth算法有分治策略，为下面提出的分布式计算提供了可能。

2 FP－Growth算法中FP－Tree挖掘过程的改进

传统的FP－Growth算法有如下优点：具有分治策略，可以分解挖掘任务或事务数据库；不需产生候选项集，并且产生树形结构，大大减少了存储空间；不需要反复扫描数据库，降低了I／O访问，提高了性能［20］。为了优化FP－Growth算法的性能，本文采用项合并策略进行剪枝优化。

该策略定义如下：如果包含频繁项集A的每个事务都包含项集B，但不包含B的任何真超集，则A∪B形成一个闭频繁项集，并且不必再搜索包含A但不包含B的任何项集［21］。

首先明确几个概念。

1）超集：如果一个集合S2中的每一个元素都在集合S1中，且集合S1中可能包含S2中没有的元素，则集合S1就是S2的一个超集。

2）真超集：S1是S2的超集，若S1中一定有S2中没有的元素，则S1是S2的真超集，S2是S1的真子集。

3）闭项集：如果一个项集X，它的真超集的支持度计数都不等于它本身的支持度计数，则X为闭项集。

4）闭频繁项集：如果闭项集的支持度大于等于最小支持度阈值，则称为闭频繁项集。

①证明A∪B＝A＝B。首先证明“包含频繁项集A的每个事务都包含项集B”意味着A是B的超集。如果B中含有一个项b，b∉A，则必存在一个只由项集A的项所构成的事务，它不包含项b，从而也就不包含项集B，与已知相矛盾。

②证明“但不包含B的任何真超集”意味着A＝B。如果A≠B，且A是B的超集，则A是B的真超集。再由“包含频繁项集A的每个事务都包含项集B”可知，每个事务都包含项集B的真超集，与已知条件矛盾。故A∪B＝A＝B。即：包含频繁项集A的每个事务都不包含A的任何真超集。这意味着包含频繁项集A的每个事务都由A且仅由A构成，不包含A的任何直接超集。所以，A的直接超集的支持度计数都不等于它本身的支持度计数。所以A是一个闭项集。由已知条件，A是一个频繁项集，所以A是一个闭频繁项集。A∪B＝A自然也是一个闭频繁项集。

由于B＝A，最后不必再搜索包含A但不包含B的任何项集，命题得证。

通过项合并策略能够大大减少搜索空间，提高挖掘频繁树的效率，也在很大程度上减少了频繁项集的数量，产生少量的频繁闭项集。

FP－Growth算法主要分为2步。

1）通过扫描整个事务数据库，计算出L频繁项集，并且按项的频繁计数从大到小排序，记为L－List。再次全量查询事务数据库，遍历每条事务数据，根据L－List做一次升序排序，然后创建节点名root为FP树的根节点，按照建立FP－Tree的流程（见图4）生成一颗完备的模式树。

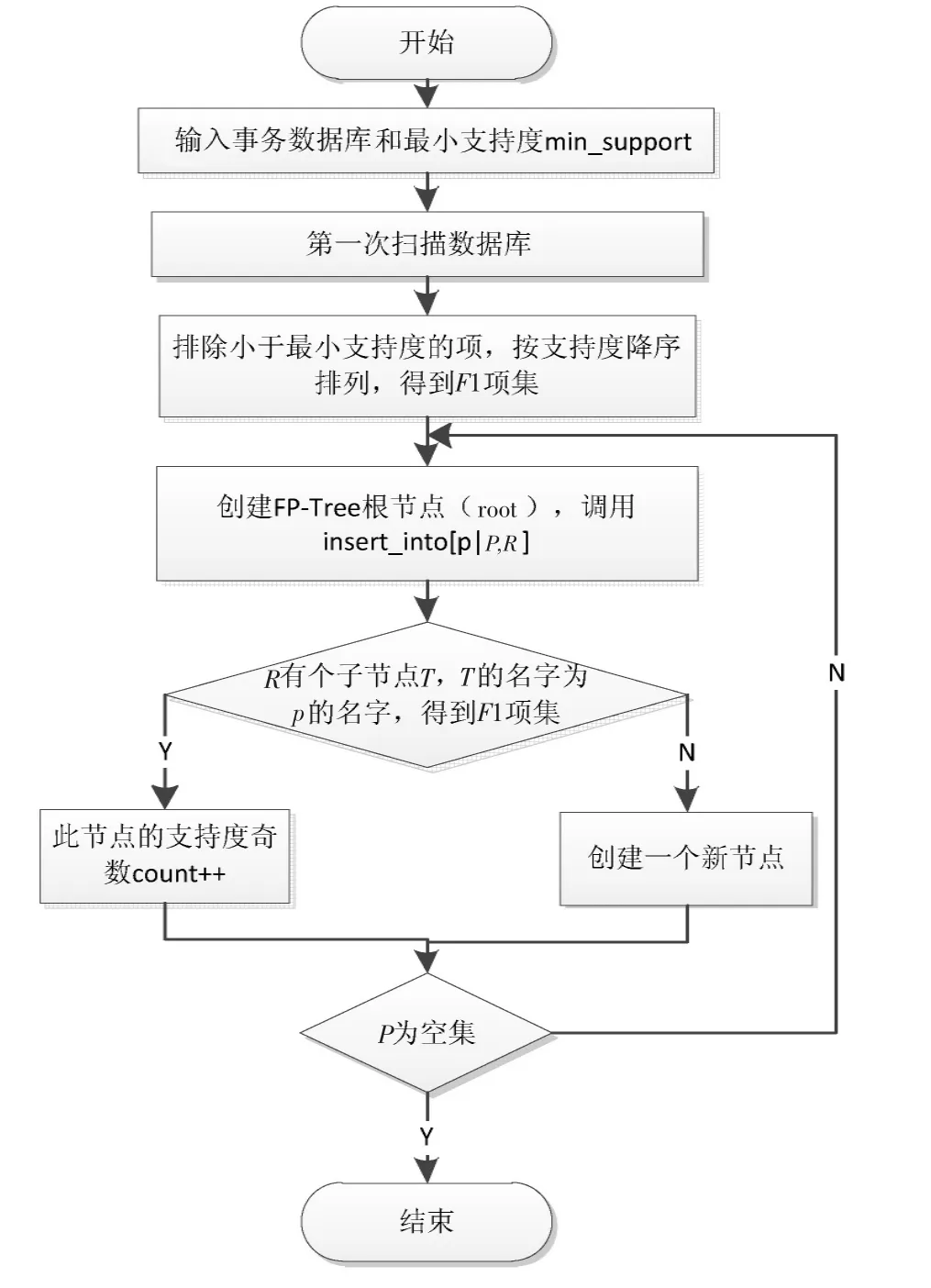
图4　创建FP－Tree的流程图Fig．4 Flow chart of FP－Tree establishment

2）开始挖掘上一步建立的FP－Tree，提出了项合并的策略来减少挖掘FP－Tree时产生的条件模式基，从而达到剪枝的效果。整个挖掘FP－Tree的流程如图5所示。

挖掘FP－Tree的步骤如下。

1）自底向上的方式遍历生成的FP－Tree的项头表，从而得到此节点的所有前缀路径，以此节点为后缀模式，得到FP－Tree中所有包含此节点的路径。

2）如果上一步得到单条路径，前缀路径的每个元素和后缀模式合并生成频繁项集。否则，需找前缀路径中是否存在项合并策略中的情况，若存在，剪枝后合并。

图5　改进的挖掘FP－Tree的流程图Fig．5 Flow chart of improved mining FP－Tree

3）以上述得到的路径作为新的数据库，重新按照创建FP－Tree的流程创建一棵新的FP－Tree，但是此时树的根节点为后缀模式，即挖掘的项。

4）把生成的树作为第1步输入数据源，反复迭代，直到最后只生成1条路径。

通过上述过程，整个FP－Tree挖掘的过程结束，挖掘出来的频繁项集都是闭频繁项集。整个过程对搜索闭项集的空间做了相应的优化，减少了树的路径，从而提高了算法的计算速度。

3 基于Hadoop的并行FP－Growth实现

面对大规模数据集，传统的FP－Growth计算的速度有所降低，虽然有研究人员提出多线程的方式来缓解计算数据的压力，但是当数据量达到一定程度时，单台计算机的内存限制成为FP－Growth算法的瓶颈。为了更好地解决单机版FP－Growth算法存在的各种问题，利用Hadoop自身处理大数据的各种优势，本研究提出基于分布式计算框架Hadoop并行计算的FP－Growth算法，很好地解决了传统FP－Growth算法的问题。图6为分布式FPGrowth算法的流程图。

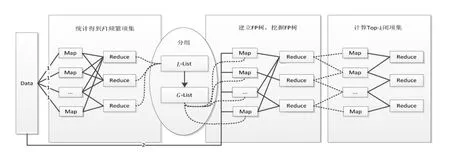
图6　分布式FP－Growth算法的流程图Fig．6 Flow chart of distributed FP－Growth algorithm

通过图6可知：分布式FP－Growth算法完美结合了MapReduce的编程思想，利用三步串行的MapReduce任务来完成，其中，结合分布式缓存机制来存储L－List表能够提高访问效率，降低相应的I／O操作。分布式FP－Growth算法的主要步骤详细描述如下。

1）统计L频繁项集

统计L频繁项集是并行算法的第1步。该步骤的主要任务是统计每个项在数据库中出现的次数，并且过滤出现次数小于设置的最小支持度的项，再把剩余的项通过出现的次数进行降序排序，最终得到L－List集合。其中L－List集合中不仅存储了项的唯一标志，而且也存储了项出现的频率，即项的计数。

统计L项集的具体处理步骤。

①Map过程：第1次全量扫描事务数据库，输入的key为每行的偏移量，value为每条事务数据。针对value的值进行分割后，输出的key为每个项，value为每个项首次出现的计数为1。

②Combiner过程：在集群的每个节点上本地化的对每个项进行1次相加统计，输出的key依旧是项，value变为本节点上项出现的次数，即计数。此过程提高了计算性能。

③Reduce过程：收集Map阶段输出的中间结果，统计每个项在整个事务数据库中出现的频率。输出的key为项的标志符，value为数据中出现的频率。图7是统计L项集的数据样式图。

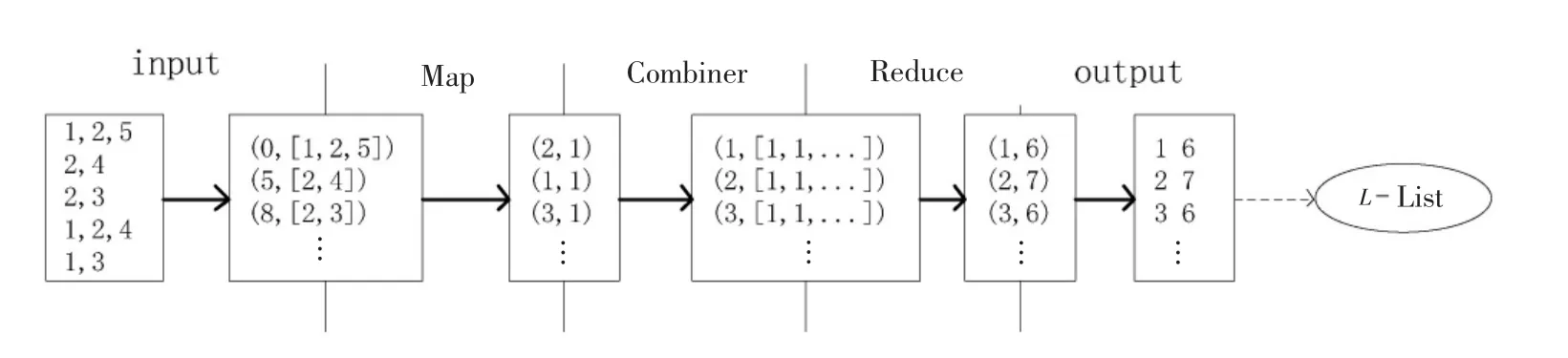
图7　L项集的数据样式图Fig．7 Data style figure of Litemsets

统计L频繁项集阶段得出的结果就是整个数据库的1频繁项集。通过每个项的计数由高到低排序后，就形成了L－List集合，并且把L－List集合存入Hadoop的分布式缓存，如此在整个集群中可以共享该文件，从而方便事务数据库分发数据，减少相应的I／O操作。为了达到每组数据的平衡和独立，利用L－List集合中的L项进行分组。

2）并行FP－Growth

图8为并行FP－Growth算法的实现步骤。通过图8可知，并行FP－Growth算法的具体过程如下。

分组和Map过程：将分布式缓存中的L－List集合存入Map中，并且对项对应的一个编号进行映射，记为i。第2次全量访问事务数据库，遍历每条事务数据中的项，通过L－List表中的L频繁项集得到一个组标志符（记为变量g），从而得到了G－List集合。

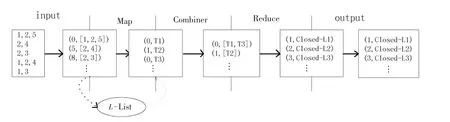
图8　并行FP－Growth算法的过程图Fig．8 Process chart of the parallel FP－Growth algorithm

其中，分组策略首先要得到每组中项的个数，记为m。

式中：m为每组中项的个数；｜F｜为L－List集合的模，即集合中项的个数；n为设定的组数。

如果式（1）不能整除，m就加上1取整数。

遍历每条事务数据中的项，依照L－List集合，先做1次排序，然后在映射表中找到项的映射数字，即i。这样，此项每组标志符计算公式如式（2）所示：

式中：g为此项将分入的组号；i为项在L－List集合中的排序号；m为每组中项的个数。

通过上述策略找到每个项对应的组，聚合每个组，从而得到G－List集合。

Map过程：在此Map阶段输出的key值为g，value为整条数据的子项集（事务序列P的子序列）。这样分组不仅均衡了整个数据库的投影数据，同时保证了挖掘过程中数据的完备性。

Combiner过程：本地聚合每组中的事务数据，形成压缩的事务数据。

Reduce过程：此阶段是整个算法中关键的一步，也是并行FP－Growth算法中具体对数据挖掘的一步，是在集群节点上运行本地化的本文改进的FP－Growth算法，但数据已不是整个事务数据库，而是子数据库。先建立FP－Tree，然后通过本文改进的挖掘算法得到频繁项集。输出的key为组号，value为挖掘出来的频繁项集。

3）聚合

图9为分布式FP－Growth算法的最后一步。

图9　挖掘K项最大的闭频繁项集的过程图Fig．9 Process diagram of mining the biggest closed frequent itemsets of Kitems

挖掘K项最大的闭频繁项集的具体步骤如下。

Map过程：本过程输入的value为挖掘出来的频繁项集。遍历频繁项集中的元素，输出的key为此元素的项，value为此频繁项集。

Combiner过程：本地化对每个项的相应频繁项集做1次排序并且选取频繁项集共同出现的频率最大的K项频繁项集。

Reduce过程：收集Combiner过程产生的局部最大的K项频繁项集，再次做排序，选取整个数据库中计数最大的K项闭频繁项集。

至此，整个分布式的FP－Growth算法完成。纵观整个分布式算法实现过程，其实是MapReduce编程模式的完美体现。这个过程清晰，但是在每一步的关键部分是被封装的，如果对一些策略要进行性能上的提升，可通过Hadoop中MapReduce计算框架的参数设定来实现性能的调优。

为了性能的提升和计算速率的提高，在整个过程中运用了分布式缓存和本地化聚合等策略。分布式的改进FP－Growth算法在处理大量的数据时速度有明显提升，这也是整个分布式计算框架最大的特性。但在处理小数据方面花费的时间要长些，所以在实现分布式的同时也为本地算法提供了具体的API，这样不仅能通过内存算法来计算小量数据，同时也可以利用并行算法来计算大规模的数据。

4 实验过程与结果

为了验证提出改进的FP－Growth算法性能，利用mushroom．dat数据来进行验证实验。mushroom．dat数据来自于Frequent Itemset Mining Data Repository［22］。实验通过FP－Growth算法和改进的FP－Growth算法在相同的最小支持度下挖掘同一份数据的速率来做比较，其中结果的横坐标数值为支持度阈值，那么最小支持度为整个mushroom．dat数据中包含的事务数据条数乘于支持度阈值，即min＿support＝transactions．number＊threshold。图10为该实验的比较图。

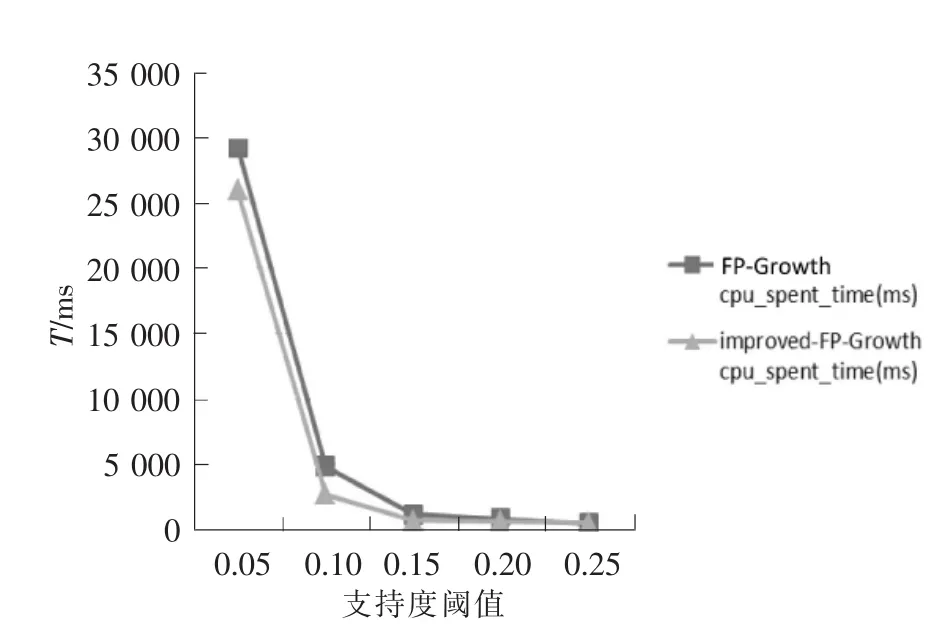
图10　挖掘速率比较图Fig．10 Mining rate comparison chart

从图10中可以看出，改进的FP－Growth算法在计算速度上有明显提高，性能较好。说明通过项合并的策略减少了搜索FP－Tree的迭代次数，实现了对搜索空间的剪枝。随着阈值的变大，相应的最小支持度计数也变大，从而得到的频繁项集的总量在减少，搜索代价也随之降低，所以改进的FPGrowth算法和FP－Growth算法在挖掘速度上很接近。因此，改进的FP－Growth算法挖掘出来的闭频繁项集数量远远少于总量的频繁项集。

验证实验的挖掘速度随着数据量的增加，挖掘速度急剧下降，到一定程度就会内存溢出。为了测试分布式改进的FP－Growth算法对大规模数据量处理能力是否提升，改进实验的数据为订单数据，此数据量最大为10 000万条。其中本实验所采用的分布式计算环境包含master，slave1，slave2，slave3 共4个节点的Hadoop集群，其中每个节点为Inter XEON Pcs（E3－1220LCPU，32GB RAM），Hadoop版本为Hadoop1．2。该实验分别从2方面来做测试。

为了反映各个数据量下分布式算法的计算速度，分别选取了10万数量级中10万和50万，100万数量级中100万和500万，1 000万数量级的1 000万，3 000万，5 000万，7 000万和10 000万。实验结果如图11所示。

图11　数据量与计算速率的折线图Fig．11 Line chart of data volume and computing rate

为了展示在同样数量级的数据中挖掘最大的K项频繁项集花费的时间情况，选取了K＝3，5，8，10和12项频繁项集。实验显示每一步的CPU计算时间的情况，使得结果更加清晰，实验结果如图12所示。

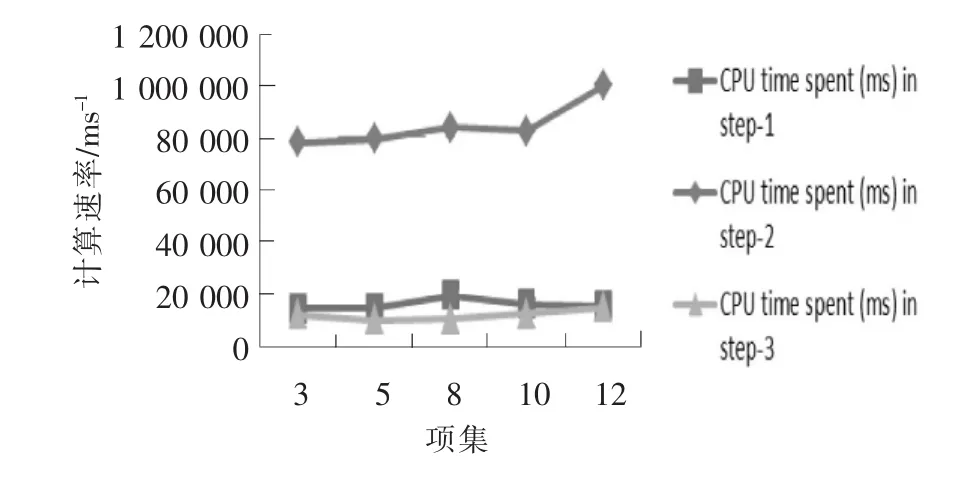
图12　K项与计算速率的折线图Fig．12 Line chart of Kand computing rate

通过实验可知：在不同数量级下基于分布式的改进FP－Growth算法的计算时间是不同的，首先是第1步在数据集的规模剧增时花费的时间相对缓慢，其次是第3步，最后是第2步，其是整个分布式算法当中最为关键的一步，也是最消耗时间的一步，这步的计算任务是非常繁重的，但在大规模数据下消耗的时间是可以接受的。至少不会出现单机运行大规模数据时出现内存溢出的情况。

实验说明了在挖掘不同最大K项频繁项集时花费的时间差距是不大的，每一步花费的时间都比较缓慢。说明分布式算法充分利用了集群的性能和内存空间，能够很好地完成大规模数据的频繁项集挖掘。

5 结 语

改进的FP－Growth算法在性能上有着明显提升，主要原因是在挖掘FP－Tree的时候通过项合并的策略来剪枝，大大减少了挖掘树迭代的次数。同时，生成的闭频繁项集相对于频繁项集的总量小了很多，减少了需在内存中占用的空间。此外，分布式改进的FP－Growth算法在处理大规模的数据量时有相当大的优势，分而治之的策略充分利用了集群的资源来实现单机无法达到的结果。

参考文献／References：

［1］ 付冬梅，王志强．基于FP－tree和约束概念格的关联规则挖掘算法及应用研究［J］．计算机应用研究，2014，31（4）：1013－1015．FU Dongmei，WANG Zhiqiang．Mining algorithm of association rule based on FP－tree and constrained concept lattice and application research［J］．Application Research of Computers，2014，31（4）：1013－1015．

［2］ 何月顺．关联规则挖掘技术的研究及应用［D］．南京：南京航空航天大学，2010．HE Yueshun．Research and Application on the Technologies in Mining Association Rules［D］．Nanjing：Nanjing University of Aeronautics and Astronautics，2010．

［3］ 施亮，钱雪忠．基于Hadoop的并行FP－Growth算法的研究与实现［J］．微电子学与计算机，2015，32（4）：150－154．SHI Liang，QIAN Xuezhong．Research and implementation of parallel FP－Growth algorithm based on Hadoop［J］．Microelectronics ＆Computer，2015，32（4）：150－154．

［4］ LAN V，ALAGHBAND G．Novel parallel method for association rule mining on multi－core shared memory systems［J］．Parallel Computing，2014，40（10）：768－785．

［5］ 杨勇，王伟．一种基于MapReduce的并行FP－growth算法［J］．重庆邮电大学学报（自然科学版），2013，25（5）：651－657．YANG Yong，WANG Wei．A parallel FP－growth algorithm based on MapReduce［J］．Journal of Chongqing University of Posts and Telecommunications（Natural Science Edition），2013，25（5）：651－657．

［6］ LIU Li，LI Eric，ZHANG Yiming，et al．Optimization of frequent itemset mining on multiple－core processor［C］／／Proceedings of the 33rdInternational Conference on Very Large Data Bases．Vienna：［s．n．］，2007：1275－1285．

［7］ AOUAD L M，LE－KHAC N A，KECHADI T M．Distributed frequent itemsets mining in heterogeneous platforms［J］．Journal of Engineering，2007（2）：1－12．

［8］ MOHAMMAD E，OSMAR R．Parallel leap：Large－scale maximal pattern mining in a distributed environment［C］／／Proceedings of the 12th International Conference on Parallel and Distributed Systems．Minneapolis：Conference Publications，2006：135－142．

［9］ 邹翔，张巍，刘洋，等．分布式序列模式发现算法的研究［J］．软件学报，2005，16（7）：1262－1269．ZOU Xiang，ZHANG Wei，LIU Yang，et al．Study on distributed sequential pattern discovery algorithm［J］．Journal of Software，2005，16（7）：1262－1269．

［10］冯汉超，周凯东．分布式系统下大数据存储结构优化研究［J］．河北工程大学学报（自然科学版），2014，31（4）：69－73．FENG Hanchao，ZHOU Kaidong．Research on optimizing big data storage structure in distributed system［J］．Journal of Hebei University of Engineering（Natural Science Edition），2014，31（4）：69－73．

［11］任家东，王倩，王蒙．一种基于频繁模式有向无环图的数据流频繁模式挖掘算法［J］．燕山大学学报，2011，35（2）：115－120．REN Jiadong，WANG Qian，WANG Meng．An algorithm based on frequent patterns directed acyclic graph for mining frequent patterns form data stream［J］．Journal of Yanshan University，2011，35（2）：115－120．

［12］刘步中．基于频繁项集挖掘算法的改进与研究［J］．计算机应用研究，2012，29（2）：475－477．LIU Buzhong．Improved apriori mining frequent items algorithm［J］．Application Research of Computers，2012，29（2）：475－477．

［13］HAN Jiawei，PEI Jian，YIN Yinwen，et al．Mining frequent patterns without candidate generation：A frequent－pattern tree approach［J］．Data Mining and Knowledge Discovery，2004，8（1）：53－87．

［14］LEE D，PARK S H，MOON S，et al．Utility－based association rule mining：A marketing solution for cross－selling［J］．Expert Systems with Applications，2013，40（7）：2715－2725．

［15］何中胜，庄燕滨．基于Apriori ＆FP－growth的频繁项集发现算法［J］．计算机技术与发展，2008，18（7）：45－47．HE Zhongsheng，ZHUANG Yanbin．Algorithm of mining frequent itemset based on Apriori and FP－growth［J］．Computer Technology and Development，2008，18（7）：45－47．

［16］NAHAR J，IMAM T，TICKLE K S，et al．Association rule mining to detect factors which contribute to heart disease in males and females［J］．Expert Systems with Applications，2013，40（4）：1086－1093．

［17］杨云，罗艳霞．FP－Growth算法的改进［J］．计算机工程与设计，2010，31（7）：1506－1509．YANG Yun，LUO Yanxia．Improved algorithm based on FPGrowth［J］．Computer Engineering and Design，2010，31（7）：1506－1509．

［18］王新宇，杜孝平，谢坤青．FP－Growth算法的实现方法研究［J］．计算机工程与应用，2004，40（9）：174－176．WANG Xinyu，DU Xiaoping，XIE Kunqing．Research on implementation of the FP－Growth algorithm［J］．Computer Engineering and Applications，2004，40（9）：174－176．

［19］陈兴蜀，张帅，童浩，等．基于布尔矩阵和MapReduce的FPGrowth算法［J］．华南理工大学学报（自然科学版），2014，42（1）：135－141．CHEN Xingshu，ZHANG Shuai，TONG Hao，et al．FPGrowth algorithm based on Boolean matrix and MapReduce ［J］．Journal of South China University of Technology（Natural Science Edition），2014，42（1）：135－141．

［20］晏杰，亓文娟．基于Apriori ＆FP－growth算法的研究［J］．计算机系统应用，2013，22（5）：122－125．YAN Jie，QI Wenjuan．Research based on Aprior ＆FP－growth algorithm［J］．Computer Systems ＆Applications，2013，22（5）：122－125．

［21］HAN Jiawei，KAMBER M．数据挖掘：概念与技术［M］．第3版．范明，孟小峰译．北京：机械工业出版社，2013．

［22］ANONYMOUS．Frequent Itemset Mining Dataset Repository ［EB／OL］．http：／／fimi．ua．ac．be／data，2012－10－21．

A novel distributed parallel FP－Growth algorithm based on Hadoop framework

ZHANG Zhenyou，SUN Yan，DING Tiefan，LIU Pengfei
（School of Information Engineering，North China University of Science and Technology，Tangshan，Hebei 063009，China）

Abstract：Aiming at the low mining efficiency and memory overflow problems of the traditional FP－Growth algorithm，on the basis of the traditional FP－Growth algorithm，a novel parallel FP－Growth algorithm is proposed，which can realize parallel processing in MapReduce programming mode of Hadoop distributed computing framework．The tested data shows that compared to the traditional algorithm，the parallel FP－Growth algorithm has great advantages：the calculation time is greatly reduced when processing the same amount of data；processed data volume is greatly increased under the same time；and memory overflow problem in large scale data mining is solved under certain conditions．

Keywords：parallel processing；distributed；data mining；closed frequent itemsets；Hadoop；FP－Growth

作者简介：张振友（1964—），男，河北唐山人，副教授，硕士，主要从事数据库及其应用方面的研究。

收稿日期：2015－11－11；修回日期：2015－12－30；责任编辑：陈书欣

文章编号：1008－1534（2016）02－0169－09

中图分类号：TP311．1

文献标志码：A

doi：10．7535／hbgykj．2016yx02013