对拟力法理论中塑性弯矩和动力方程的分析与讨论

束忠文, 曲激婷

(大连理工大学 土木水利学院, 辽宁 大连　116024)



对拟力法理论中塑性弯矩和动力方程的分析与讨论

束忠文, 曲激婷

(大连理工大学 土木水利学院, 辽宁 大连116024)

摘要:探讨了拟力法理论中塑性弯矩表达式的理论意义,引入塑性刚度对公式进行修正,得到修正后的拟力法基本公式.最后,以数值分析算例比较了改进前后两种方法的计算结果.结果表明,修正的拟力法计算结果偏于安全,不仅保留了拟力法计算效率高的优点,公式物理意义更易被理解.

关键词:动力分析; 拟力法; 塑性弯矩; 有限元法; 等效塑性刚度

拟力法最早由Lin等人[1]于1968年提出,是一种变位移的非线性分析方法.其核心思想是利用初始刚度代替变刚度,与传统变刚度法相比,具有运算速度快、收敛性好、计算稳定性高且材料适用性广等优点.Wong和Yang[2]于1999年将拟力法应用于钢框架结构的动力弹塑性分析,假定结构进入塑性状态时,塑性变形只发生在结构构件端部,其他部位保持弹性;塑性变形区利用塑性铰概念描述,结构塑性位移由塑性铰转动引起,通过塑性铰与结构水平位移及恢复力之间的关系来实现非线性求解.随后,Wong[3]等人在已成熟的拟力法理论基础上,将其应用到框架结构的能量分析中,推导出塑性耗能公式,可获得任意时刻滞回耗能在结构各构件上的分布情况,为能量分析方法开辟了新途径.2005年,Wong等人[4-5]又将拟力法应用到结构的线性预测优化控制中,解决了主动控制的时滞问题,可以得到良好的控制效果,且该方法计算高效的优点体现得更加充分.2007年,Chao[6]等人在拟力法基本理论基础上提出了改进的计算模型,采用三个塑性机制模拟钢筋混凝土梁柱单元,考虑框架柱的P-delta效应,同时考虑了构件在反复载荷下的刚度退化问题.李钢等[7]将拟力法运用到消能减震结构的地震反应分析,为消能减震结构的地震分析提供了一种新的途径.目前,拟力法的非线性计算理论得到国内外很多学者的关注,已经逐渐发展起来,研究队伍也越来越壮大.本文主要针对拟力法基本理论进行讨论分析,引入塑性刚度对塑性弯矩计算公式进行修正,并推导了修正后的拟力法基本公式,最后,通过数值算例分析对修正前后的拟力法计算结果进行对比分析.

1拟力法基本理论及改进

1.1拟力法基本理论

Wong等人[2]最先将拟力法应用于钢框架结构体系的分析,并对拟力法基本原理进行了详尽的阐述,构件采用双线形的力-变形关系,位移x(t)分为弹性位移x′(t)和塑性位移x″(t).单自由度体系在外力F(t)作用下,结构变形可分解为弹性变形、虚拟外力Fa(t)作用下产生的塑性变形以及塑性铰处转动作用下的变形.虚拟外力Fa(t)与支座反力FRT(t)应满足:

(1)

因此,可得到塑性转角与塑性位移的关系:

(2)

弹性变形阶段弯矩为

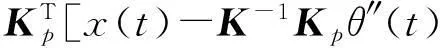
(3)

由塑性转动变形引起的弯矩为

(4)

式(1)～式(4)中,K为构件的初始刚度;θ″(t)为塑性铰处转角;Kp为塑性转角变形与支座反力之间的刚度矩阵;KR为塑性铰转角与塑性铰处弯矩之间的刚度矩阵.

塑性转角自由度处由虚拟外力引起的弯矩为

(5)

塑性变形阶段的弯矩为

(6)

由式(1)～式(6)可得出总弯矩和力的关系式:

(7)

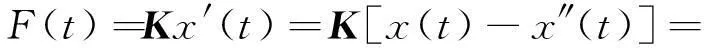
(8)

由于式(7)和式(8)包含三个未知量,两个方程无法求解,因此需要另一个关系式才能得出各个量的唯一解,而此补充方程可通过弯矩与塑性转角θ″(t)的关系建立.常用的刚性铰塑性弯矩与转角关系分为强化刚性铰和一般刚性铰两种,本文采用的是理想铰模型.

对一个具有n个自由度的结构,拟力法基本公式为

(9)

1.2关于拟力法理论的讨论

从上述拟力法的理论推导可看出其核心思想是通过利用初始刚度代替传统的变刚度来求解结构的非线性,从而减少刚度变化需要的存储空间,对求解速度有很大提高,而且可以求解结构各个构件塑性变形的大小.但如文献[2]中所阐述,拟力法在求解塑性弯矩M″(t)时,根据公式(4)和式(5),MRT(t)和Mp(t)求解使用的都是初始刚度Kp和KR,从物理意义上比较难以理解.对于双线性的力-位移关系,结构杆件屈服后的刚度(EI)比初始刚度小,故计算塑性弯矩时使用初始刚度会导致结果的偏差.

假设相应于K和Kp屈服后的刚度分别为K′和Kp′,在同一变形状态下可认为Kp′/K′=C( C为一常量),C与结构构件长度等因素有关.同理,可以推得Kp/K=C.以一个单层单跨结构(参数如图1所示)的刚度矩阵为例,其刚度矩阵可以根据式(10)和式(11)求解.设其塑性状态下平均刚度为EIp1、EIp2,替换公式中的EI1和EI2,得到塑性刚度矩阵,可近似认为EI1/EIp1= EI2/EIp2=a,故有K=aK′,Kp=aKp′.从而,

(10)

(11)

因此,得到拟力法中公式变换的重要等式

(12)

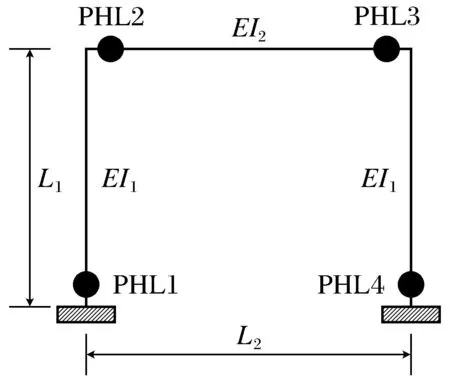
图1　单层单跨结构模型及参数

1.3拟力法基本公式的初步修正

根据对拟力法中塑性弯矩的计算,引入塑性等效刚度[8],对拟力法的基本公式进行修正.以矩形截面的构件为例,一般情况下,当结构受到外力作用,构件某处截面达到屈服应力时,弯矩达到屈服弯矩My,此时曲率的计算公式为

(13)

式(13)中,φy为屈服曲率,εy为屈服应变,d为截面有效高度,c为受压边缘到中性轴的高度,EIe l为构件的弹性刚度.

由式(13)可得,

(14)

(15)

当弯矩达到极限弯矩时总曲率为

(16)

式中,εcu为混凝土极限应变,φp为塑性部分的曲率.得到塑性部分的曲率后,可近似求解塑性等效的刚度

(17)

利用此等效塑性刚度EIp l修正拟力法中的塑性弯矩公式中的弹性刚度EI,可求解各个刚度矩阵,得到修正后的拟力法基本公式如下:

塑性转角弯矩

(18)

塑性位移弯矩

(19)

塑性弯矩

(20)

弹性弯矩

(21)

因此,总弯矩为

(22)

(23)

总弯矩计算公式可以写成

(24)

最后得到修正后的基本公式:

(25)

此动力方程与原拟力法公式形式相同,运用状态空间计算方法可以求解结构的动力时程曲线.

2数值分析

选用文献[9]中的一个单层单跨钢筋混凝土框架,混凝土设计等级强度为C35,梁柱的截面尺寸均为300 mm×400 mm,梁的纵筋为3C18,柱的纵筋为3C25,箍筋均为Φ6@200,柱高为5 m,梁长度为5 m,设置四个塑性铰,位置分别在梁的两端和柱的根部,如图1所示.梁柱端部截面弯矩与曲率参数见表1.

采用MATLAB编程计算,两种方法下框架结构在30 s的El-Centro地震波下顶点位移时程曲线如图2所示,单位力与位移关系及弯矩与塑性转角关系曲线分别如图3和图4所示.

表1　梁柱截面的弯矩曲率参数和塑性铰等效长度

注:对称配筋时,塑性铰的等效长度取截面有效高度

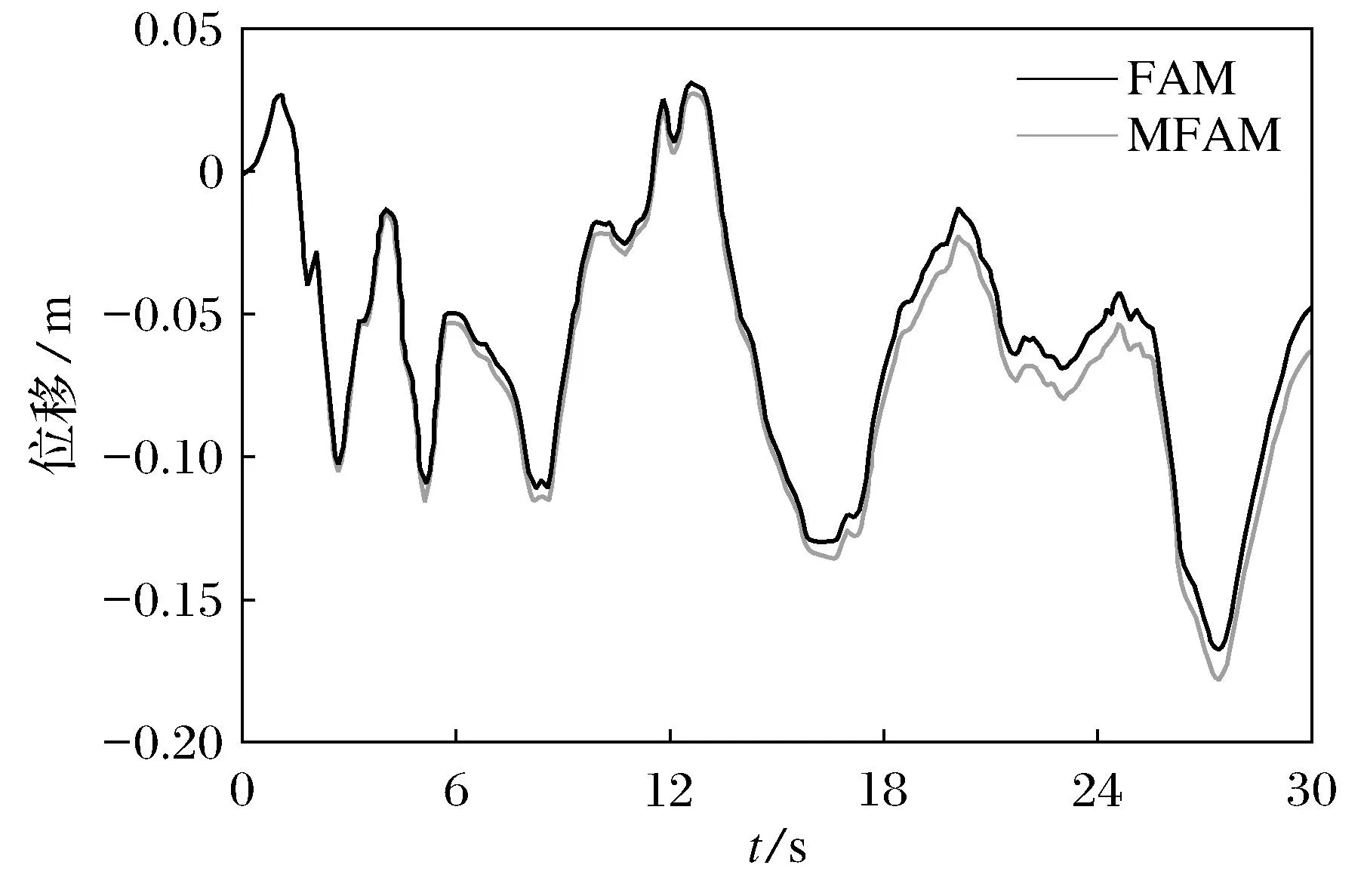
图2　改进的拟力法与原拟力法计算所得结构顶点

从图3中两条曲线对比分析中可知,开始处于弹性阶段,两曲线重合,大约从第6 s开始结构出现塑性铰,修正后的拟力法与原拟力法计算顶点位移有偏差,塑性变形越大偏差越大.由于修正后拟力法使用等效塑性刚度,比初始刚度小,相同的力作用下,位移较大,从图中曲线的后半段可看出这点.采用修正后的拟力法计算本文算例得到的位移与原拟力法偏差不大,两者的位移峰值都出现在第27.3 s,偏差为6.2%.就理论推导而言,采用等效塑性刚度修正的塑性弯矩计算物理意义更容易被理解.就计算效率而言,此算例原拟力法的计算时间大约为0.122 141 s,修正后的拟力法计算时间约为0.132 620 s,可见保留了拟力法计算效率高的优点.

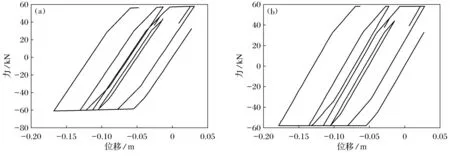
图3　力位移关系曲线

图4　塑性铰3处弯矩与塑性转角关系曲线

3结语

(1) 对拟力法理论中的塑性弯矩计算公式进行探讨,引入等效塑性刚度的概念对塑性弯矩求解公式进行修正,物理意义更易理解,并推导了修正后的拟力法基本公式.

(2) 通过数值算例计算,比较了修正前后拟力法的计算结果,结果表明修正后拟力法的计算位移较大,偏于安全.

(3) 拟力法和有限元法一样都是一种近似求解结构非线性的工具,在工程可接受的误差范围内,拟力法计算时间更短,需要的计算储存更小.

参考文献:

[1] LIN T. Theory of inelastic structure[M]. New York: John Wiley & Sons, 1968.

[2] WONG K K F, YANG R. Inelastic dynamic response of structures using force analogy method[J]. Journal of Engineering Mechanics, 1999,125(10):1190-1199.

[3] WONG K K F, WANG Y. Energy-based design of structures using modified force analogy method[J]. The Structural Design of Tall and Special Buildings, 2003,12(5):393-407.

[4] WONG K K F. Predictive optimal linear control of elastic structures during earthquake. Part I[J]. Journal of Engineering Mechanics, 2005,131(2):131-141.

[5] WONG K K F. Predictive optimal linear control of inelastic structures during earthquake. Part II[J]. Journal of Engineering Mechanics, 2005,131(2):142-152.

[6] CHAO S, LOH C. Inelastic response analysis of reinforced concrete structures using modified force analogy method[J]. Earthquake Engineering & Structural Dynamics, 2007,36(12):1659-1683.

[7] 李钢,李宏男,李瀛. 基于拟力法的消能减震结构地震反应分析[J]. 土木工程学报, 2009(4):55-63.

(LI G, LI H N, LI Y. Analysis of seismic response of structures with dissipation devices by using fictitious force method[J]. China Civil Engineering Journal, 2009,42(4):55-63.)

[8] HUANG C L, LI Y F, LIN C T, et al. Analytical and pushover analysis for predicting nonlinear force-displacement relationships of slender RC walls[J]. Journal of the Chinese Institute of Engineers, 2011,34(3):415-428.

[9] 刘哲锋,沈蒲生,龚胡广. 基于拟力法的框架结构静力弹塑性分析[J]. 建筑科学与工程学报, 2006(3):32-36.

(LIU Z F, SHEN P S, GONG H G. Static elastic-plastic analysis of frame structure based on force analogy method[J]. Journal of Construction Science and Engineering, 2006(3):32-36.)

【责任编辑: 祝颖】

Analysis and Discussion on Plastic Moment and Equations of Force Analogy Method

ShuZhongwen,QuJiting

(School of Civil Engineering, Dalian University of Technology, Dalian 116024, China)

Abstract:The theoretical significance of plastic stiffness of force analogy method (FAM) is presented after anlalyzing the physical significance of plastic moment and the equation of plastic moment is modified. Then, according to the improvement of plastic moment, the basic equations of the FAM are derived. Numerical examples are illustrated to compare the results of the original equations of FAM and modified ones. The analysis results indicate the modified FAM is still effective and easy to be understood theoretically.

Key words:dynamic analysis; force analogy method; plastic moment; finite element method; equivalent plastic stiffness method

中图分类号:TU 318

文献标志码:A

文章编号:2095-5456(2016)02-0155-05

作者简介:束忠文(1991-),男,安徽安庆人,大连理工大学硕士研究生.

基金项目:国家自然科学基金资助项目(51108064).

收稿日期:2015-09-25