基于残差主元分析的多变量系统故障诊断方法及应用

高　会, 李彦平

(沈阳大学 装备制造综合自动化重点实验室, 辽宁 沈阳　110044)



基于残差主元分析的多变量系统故障诊断方法及应用

高会, 李彦平

(沈阳大学 装备制造综合自动化重点实验室, 辽宁 沈阳110044)

摘要:通过建立多变量系统偏差自回归模型,提出一种基于残差加权主元分析的多变量系统故障诊断方法.这种方法既可消除偏差数据的自相关性,又可弥补其他主元分析所带来的缺陷.应用实例仿真结果表明,其具有良好的故障诊断效果.

关键词:多变量系统; 故障诊断; 偏差模型; 残差加权; 主元分析

主元分析(Principal Component Analysis,PCA)是多变量系统统计分析常用的方法之一[1], 该方法也是在数据量大、数据维数高、变量间具有相关性的连续过程中, 用当前过程信息来判断系统状况[2], 实现故障诊断的有效方法. 它被广泛应用于化学、经济学及模式识别图像处理[3]等领域, 在不同的领域也进行了相应拓展[4]. 在工业过程中直接对工业采集到的数据进行操作, 计算量非常大, 降低了故障检测系统的实时性. 而PCA方法能够提取原始数据中的主要信息, 将高维数据降为低维数据, 同时又能够保存原有数据的主要信息, 提高故障检测系统的有效性[5].

工程实践表明,可通过过程变量的偏差值反映多变量系统发生的故障情况.但这种偏差值常常存在自相关性,而这种自相关性会造成对故障的一种误判.为此可建立偏差自回归模型,通过偏差样本获得模型残差信息.模型残差作为模型噪声的一种估计,能够真正反映系统故障的有效信息.

本文提出一种基于残差加权主元分析的多变量系统故障诊断方法.这种方法可消除偏差自相关性,弥补其他主元分析所带来的缺陷.再者,对残差数据进行加权处理,可使其产生的残差主元模型更加符合实际情况.残差加权主元分析方法应用在多变量系统故障诊断上,能准确判断系统出现故障.进而结合此时信号的形态,即可找出故障发生部位与类型.

1多变量系统偏差模型

对一个多变量系统,可以选取一组变量或向量x(t)∈Rm来对系统进行全局或局部的描述.称系统在正常运行情况下的x(t)为标称值[6],记为x*(t).实际上,由于存在扰动或出现故障,系统运行实际x(t)与标称值x*(t)之间产生偏差ξ(t):

(1)

偏差时间序列{ξ(t)}存在自相关性.这种相关性可以用其前p步的值ξ(t-1),ξ(t-2),…,ξ(t-p)线性组合表示.为此,假设偏差值ξ(t)为一个平稳随机过程,且近似满足p阶自回归模型:

(2)

其中,ε(t)～N(0,Σ)

(3)

如果x(t)是多变量系统的一个全局性的描述,则式(2)为一阶自回归模型.可用最小二乘法进行{Ai}的参数估计:

(4)

由此,可得到残差模型:

(5)

这里,模型残差e(t)是对噪声ε(t)的一个估计.本文的残差值带有特定的定义,与其他文中的残差[7]是不同的概念.

2残差PCA基本原理

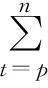
(6)

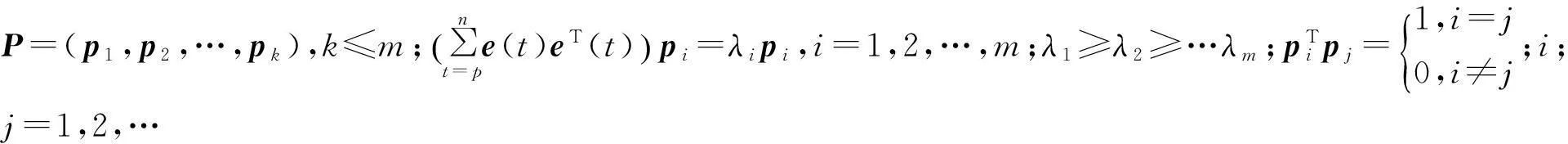
显然,

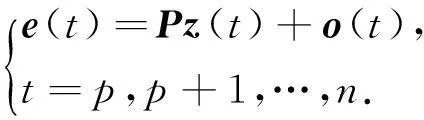
(7)

式中,

(8)

若设

(9)

(10)

(11)

则式(6)～式(8)可分别用矩阵表示为

(12)

(13)

(14)

其中,P满足

(15)

(16)

(17)

(18)

(19)

(20)

由式(12)～式(14)知,

(21)

这里,式(13)或式(21)为En的正交分解.其中,前项PZn是En的k个主成分,也是其在Span{P}空间上的投影.

通常采用主元累计贡献率法来确定主元数目k,即

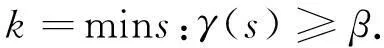
(22)

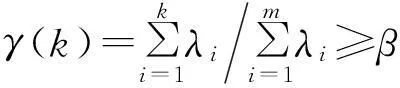
(23)

3残差加权主元分析

在工程实际应用中,残差样本数据的可信度可能存在差异,为此需要进行残差加权处理,然后再对其进行主元提取:

(24)

这里,w(t)∈[0,1]为加权系数.

由此,可建立残差加权主元模型:

(25)

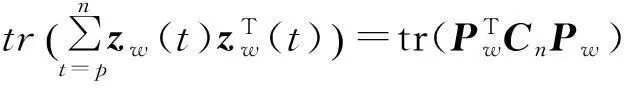
(26)

如果选择w(t)2=ρn-t,ρ∈(0,1],则算法变为指数衰减加权残差主元分析,显然

(27)

4多变量系统的故障诊断

基于多变量系统偏差自回归模型,状态偏差的产生取决于模型噪声或系统受扰情况.当系统出现故障异常时,意味着系统受到很大的扰动,势必会产生较大的偏差.如图1所示,对于前14组系统稳定运行的数据,其偏差较小且在0附近波动;在其时刻之后给一扰动,那么偏差发生较大波动,系统处于故障情形,不再满足稳定运行的分布.

假设系统稳定运行时偏差模型噪声ε(t)～N(0,Σ),则有

(28)

(29)

式中,Ω为对角矩阵;且满足

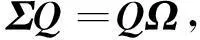
(30)

(31)

(32)

或者

(33)

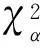
(34)

否则,可判定系统出现故障.

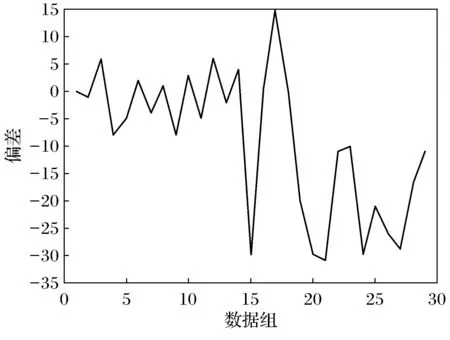
图1　偏差示意图

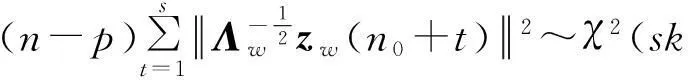
(35)

依据初始假设条件,基于残差加权主元分析的多变量系统在满足下式的情况下出现故障:

(36)

5残差PCA算法的应用

5.1算法诊断步骤及脉络

(1) 首先选择实际测量得到的正常样本数据,对数据进行偏差自回归模型的处理得到残差数据,再求取均值;

(2) 求取残差数据协方差矩阵的特征值和特征向量,按从大到小的顺序排列特征值,并对应地排好特征向量;

(3) 确定主元个数和负荷向量;

(4) 保存过程变量的均值、负荷向量及负荷向量对应的特征值.

在离线状态下处理数据:

(1) 选取一段时间的采样数据初步处理后获得残差,利用保存的均值处理当前残差数据的每个变量;

(2) 对处理后的数据代入进行残差主元分析,也就是乘以负荷向量得到主元;

(3) 按式(32)、式(33)或式(35)计算当前样本的χ2值;

(4) 比较对应自由度χ2分布的临界值,如果出现式(34)的情形,系统运行正常;否则故障.或者出现式(36)的情况,则系统故障;否则正常.

本文多变量系统故障诊断脉络图如图2所示.

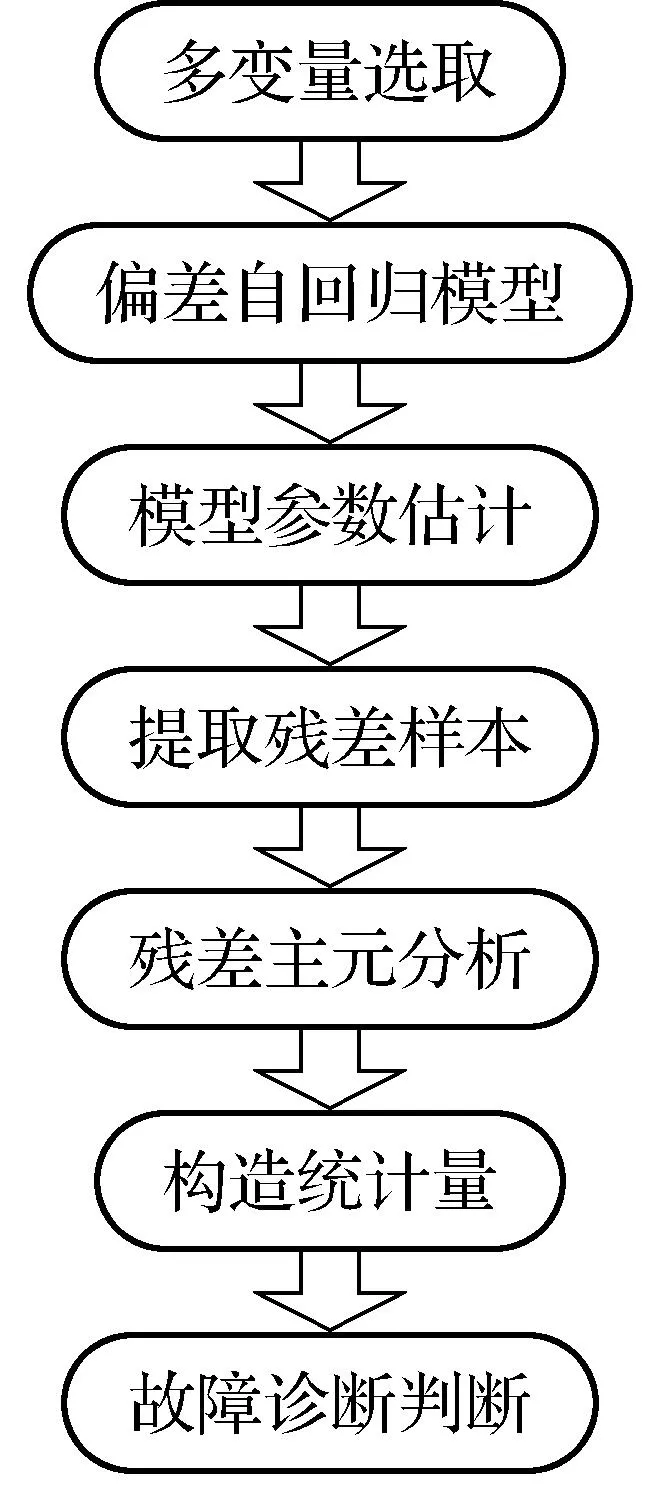
图2　多变量系统故障诊断脉络图

5.2算法仿真

以浆体管道输送系统作为多变量系统的故障诊断对象.浆体管道输送系统中有压力、流量、电流、浮球位移、矿浆高度等多个变量显示浆体管道输送系统的运行状况.此次选择易于检测的3个变量进行试验.表1中列出了11组数据中5组数据的实测值和标称值.

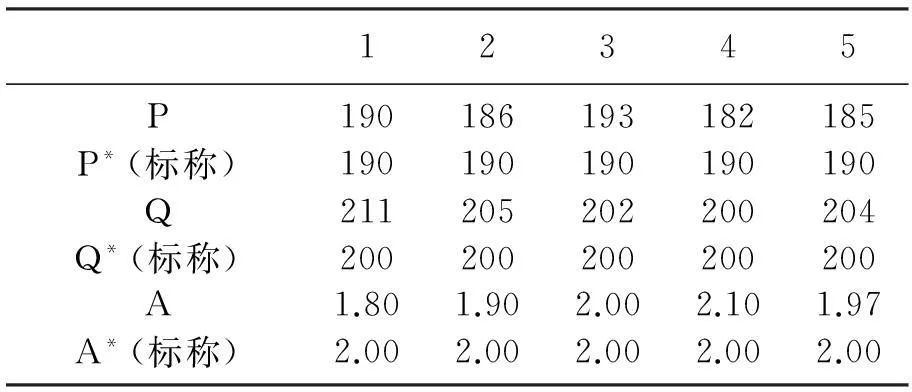
表1　变量数据和标称值

11组样本数据经过偏差处理建立自回归模型,在p=2时得到的9组残差数据见表2.

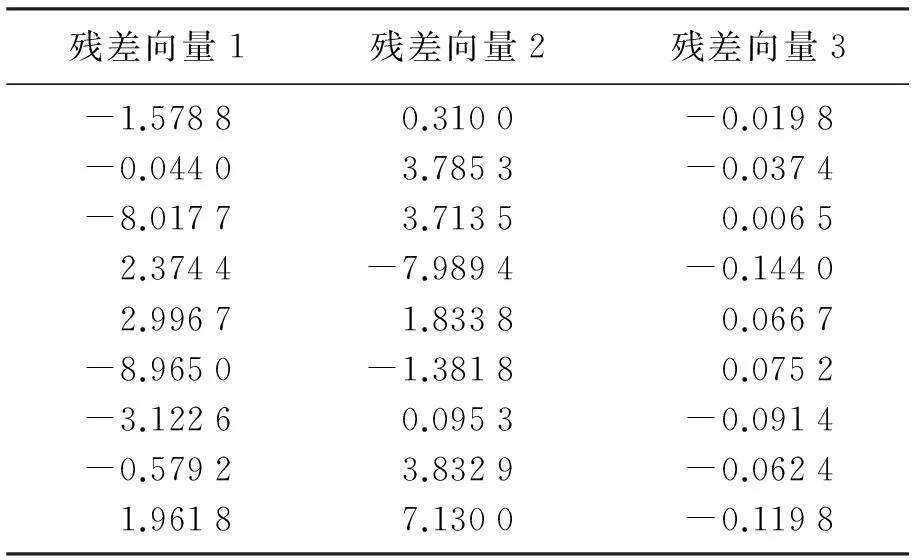
表2　残差数据

采集11组系统正常工作时的数据,选取24组新观测数据作为测试数据,其中前14组正常数据和后10组故障数据.10组故障数据的种类见表3.图3是24组测试数据经PCA用统计量处理的结果,图4是采用偏差数据加权后PCA处理的结果.可以看出前14组正常数据有少数超过阈值,整体检测效果不太理想,可能会产生误报漏报.

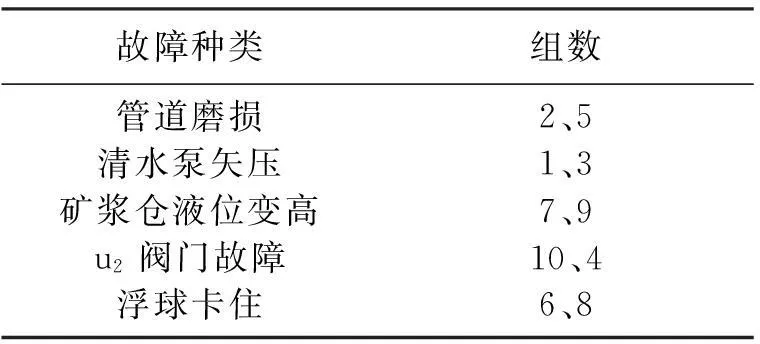
表3　数据的故障分类

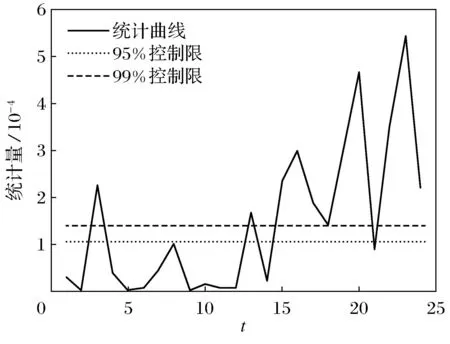
图3　PCA算法故障诊断

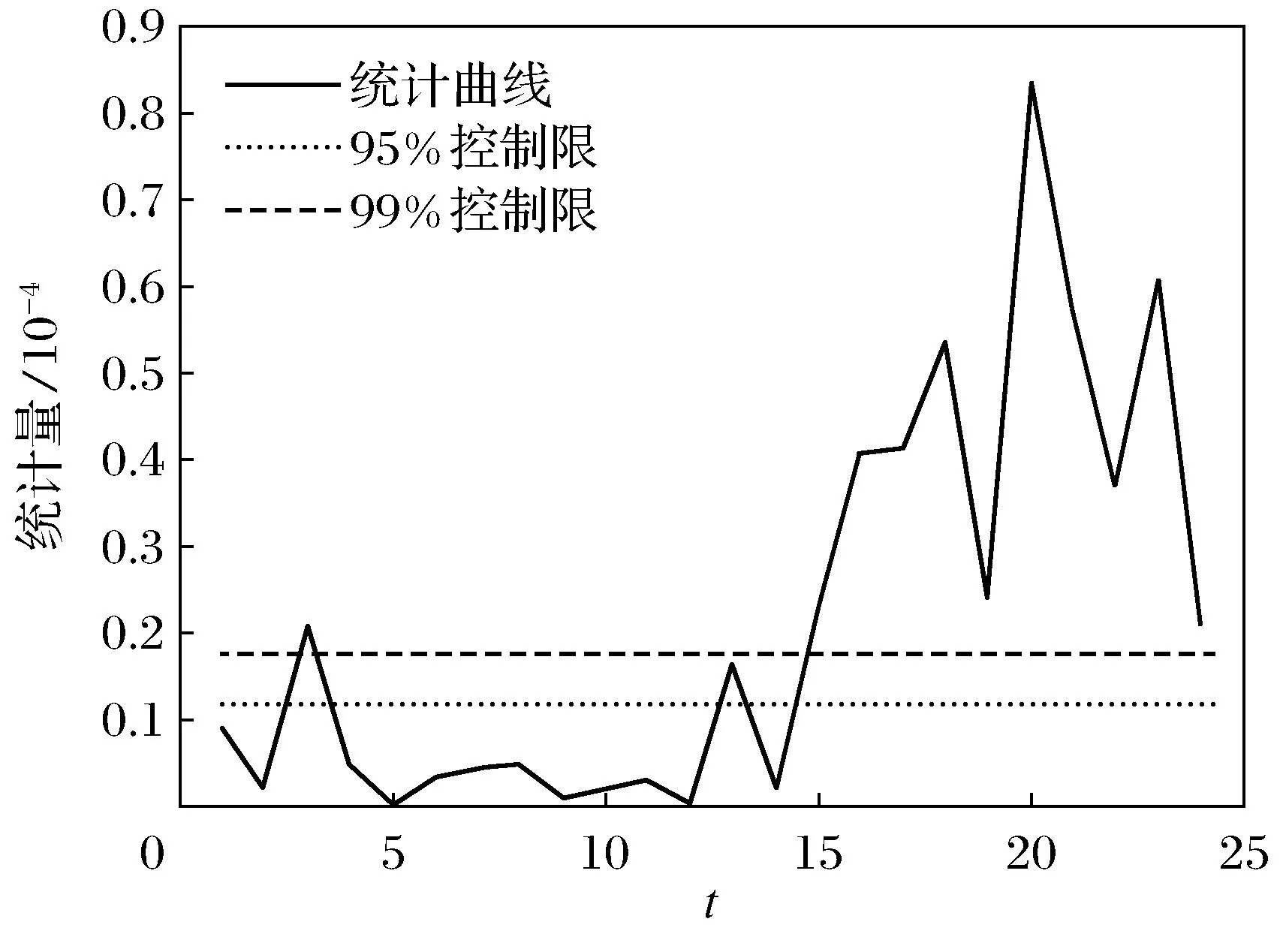
图4　加权PCA算法(ρ=0.2)

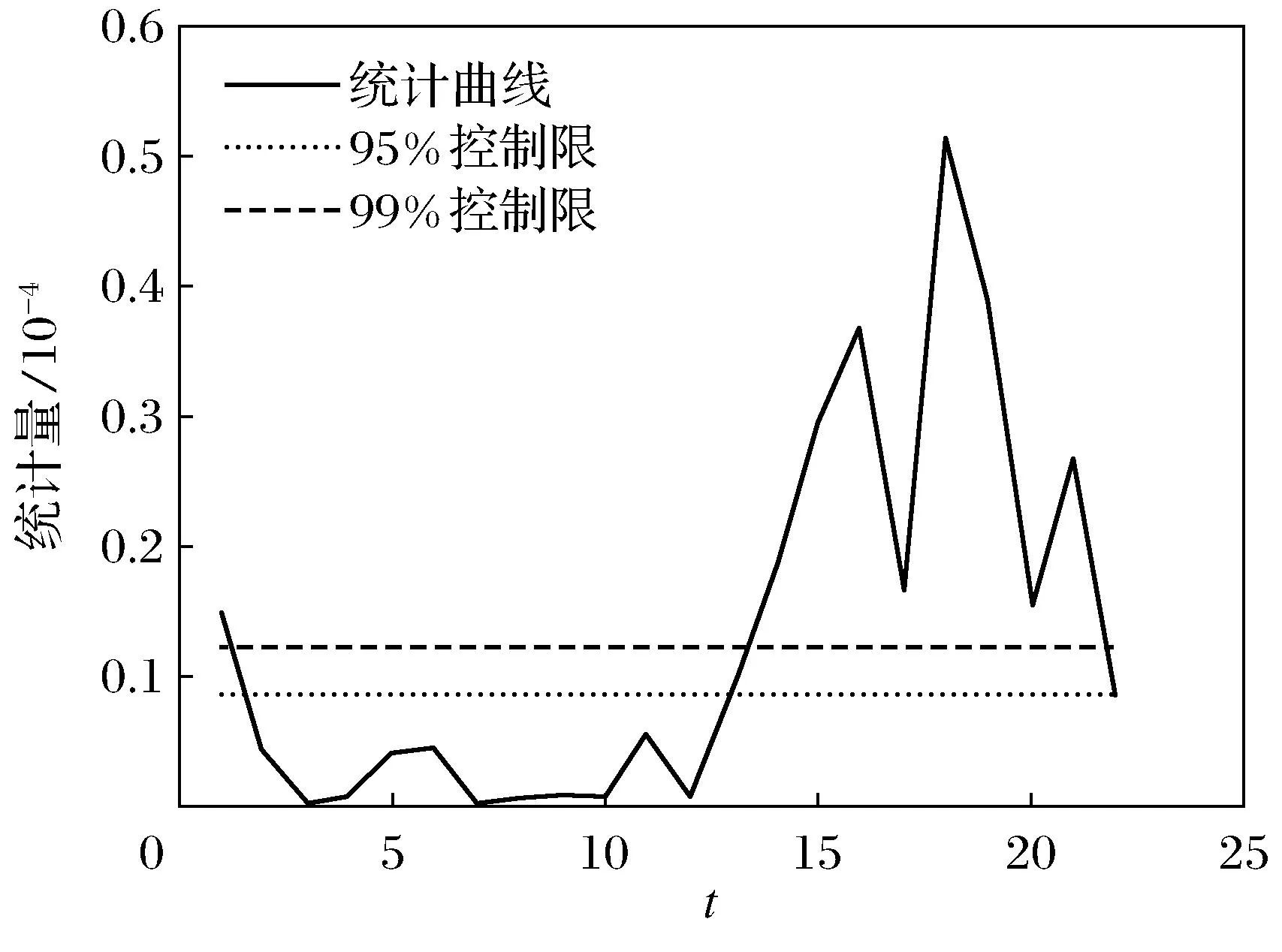
图5　残差PCA算法故障诊断(ρ=1)

采用同样的样本数据,按第一节方法求得残差值,作为训练数据.图5是残差PCA算法的诊断结果,图6是加权系数ρ=0.2时残差PCA算法的诊断结果.图6与图3～图5相比较可以看出前14组正常数据几乎没有超过阈值,并且之后的数据诊断效果非常好.

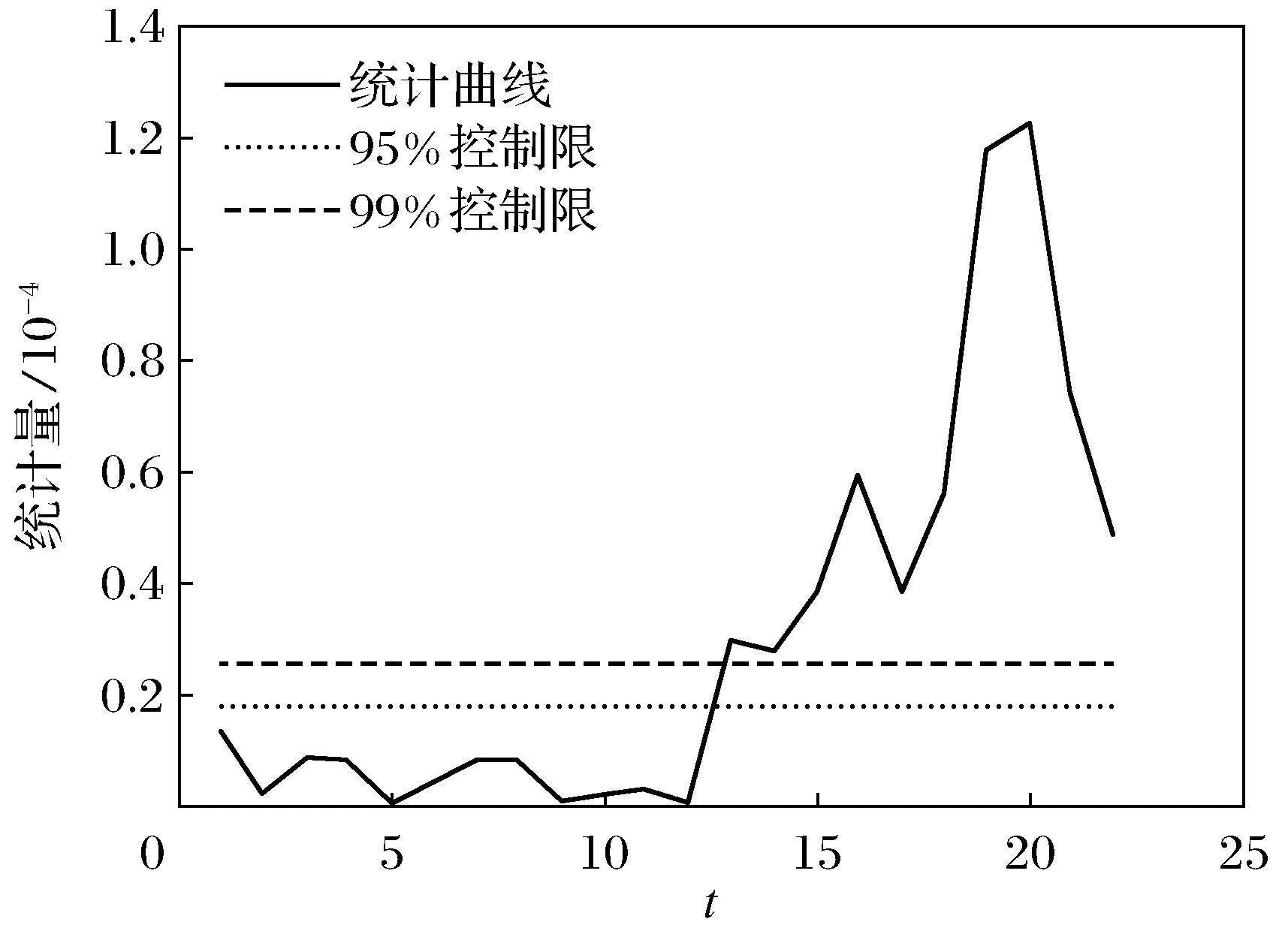
图6　加权残差PCA算法故障诊断(ρ=0.2)

5.2浆体输送系统的故障诊断

残差加权主元模型能够准确迅速地检测出系统故障.在此基础上结合不同时刻信号的形态,可以快速及时地发现故障部位.以浆体管道的故障诊断为例进行说明.当通过残差主元分析发现系统出现故障,从图7a中浮球的运行信号形态,可以推断此时触顶故障,发生原因在隔离罐外部,是外部因素导致的故障.如果出现图7b的信号形态,即系统隔离罐中浮球处于运行卡住的故障,那么判断出此时故障是由于隔离罐设备本身引起的.

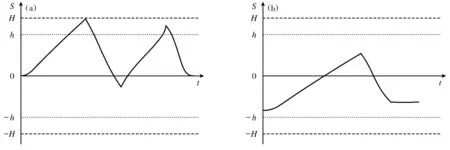
图7　浮球运行信号轨迹

在浆体管道输送系统中,发生故障后出现图8中的矿浆仓液位信号,此时液位急剧变高,推断矿浆输入控制出现故障,应立即对其相应部位检查.

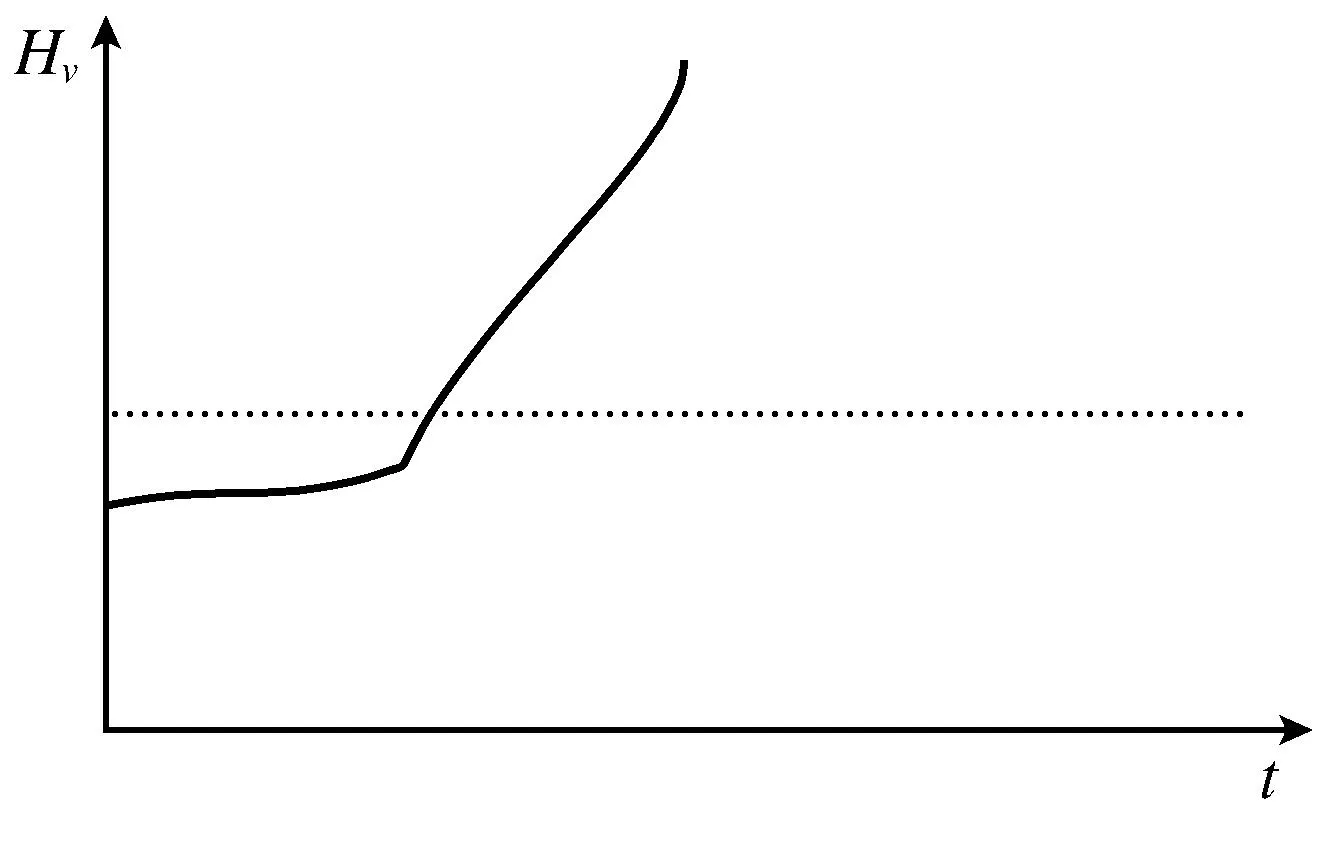
图8　矿浆仓液位信号轨迹

对浆体管道输送系统的管道压力和流量信号形态分析.因为系统存在吸浆和排浆两个过程,两个过程对应变量不同,下面只分析排浆过程的故障.在图9a中,推断电磁阀或者单向截止阀存在故障;图9b中排浆管道有流量无压力,系统的清水泵矢压或排浆管道漏浆;图9c中排浆管道有压力无流量,阀门u2控制出现故障或者管道堵塞.

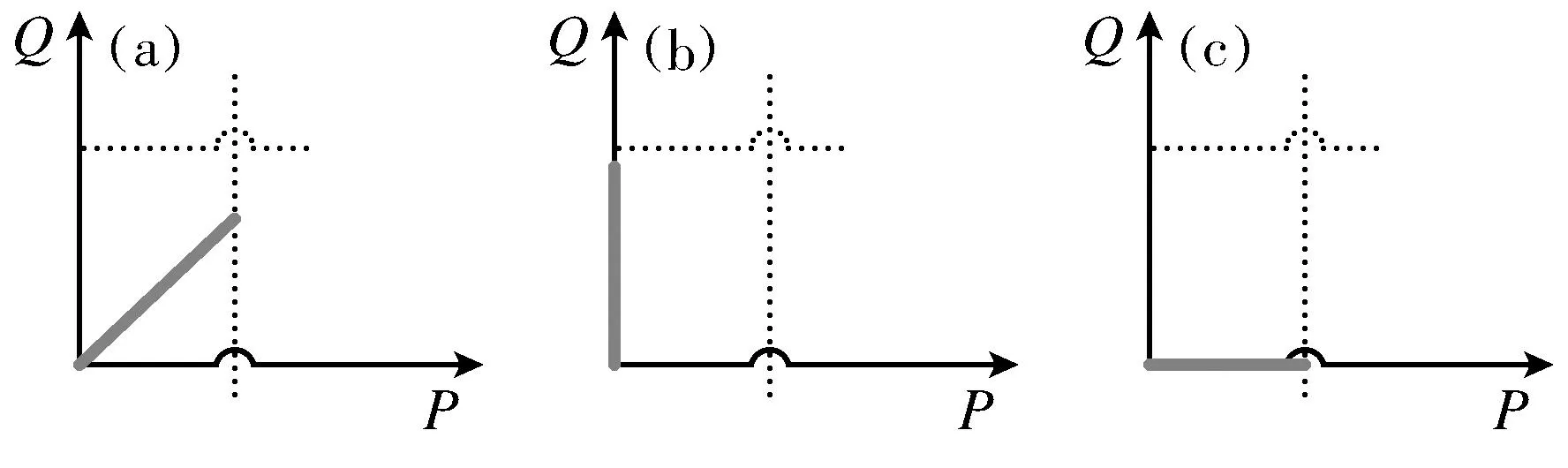
图9　P-Q信号轨迹分析

对浆体管道输送系统进行全面准确的故障诊断还要结合其他信号的形态.下面对10组故障数据结合相应时刻的信号形态进行诊断.

在第1、3组故障数据出现时系统出现了图9b的信号形态,经检查确认是清水泵矢压引起的故障.第2、5组故障数据出现了图9b的信号形态,对清水泵和管道检查后发现是管道出现磨损故障.第4、10组故障数据出现了图9c的信号形态,经排查后确实阀门u2出现故障.第7、9组故障数据出现了图6的信号形态,确认是矿浆仓液位变高.第6、8组故障数据出现了图7b的信号形态,经检查是浮球在隔离罐中被卡住.

6结论

本文通过建立多变量系统偏差模型,获取模型残差样本信息,并基于残差主元分析对多变量系统故障诊断问题进行深入研究.根据实际问题需要,可对不同残差数据进行加权处理,以提取更有效的故障信息,为此提出残差加权主元分析算法.采用残差加权主元分析算法和信号形态分析相结合方法,可以有效实现多变量系统的故障诊断.

参考文献:

[1] 周游,李元,杜志强. 一种指数加权主元分析算法的研究[J]. 沈阳化工学院学报, 2007,21(2):137-139.

(ZHOU Y, LI Y, DU Z Q. A research about index weighted principal component analysis algorithm[J]. Journal of Shenyang Institute of Chemical Industry, 2007,21(2):137-139.)

[2] 邱天,白晓静,郑茜予. 多元指数加权移动平均主元分析的微小故障检测[J]. 控制理论与应用, 2014,409(2):19-26.

(QIU T, BAI X J, ZHENG Q Y, The small fault detection by multiple index weighted moving average principal component analysis[J]. Control Theory and Application, 2014,409(2):19-26.)

[3] 刘美玲. 基于多元统计分析的过程故障诊方法研究[D]. 南京:南京理工大学, 2013:20-48.

(LIU M L. Process of fault diagnosis method based on multivariate statistical analysis research[D]. Nanjing: Nanjing University of Science and Technology, 2013:20-48.)

[4] 唐勇波,桂卫华,彭涛. PCA和KICA的特征提取变压器故障诊断模型[J]. 高压电技术, 2014,40(2):57-56.

(TANG Y B, GUI WH, PENG T. Feature extraction of PCA and KICA for transformer fault diagnosis model[J]. High Voltage Technology, 2014,40(2):57-56.)

[5] HE Q, WANG J. Statistics pattern analysis: a new process monitoring framework and its application to semiconductor batch process[J]. Biogeosciences, 2011,57(57):107-121.

[6] 何时伟, 王瑞宝, 丁翔. 标称值代替示值计算数表最大允许误差的研究[J]. 计量与测试技术, 2014,32(1):46-48.

(HE S W, WANG R B, DING X. Study of the allowable error for nominal value instead of the calculated value[J]. Measurement and Testing Technology, 2014,32(1):46-48.)

[7] 孟兆佳, 岳晓宁, 原忠虎. 基于多层回归分析城市雾霾成因模型[J]. 沈阳大学学报(自然科学版), 2015,27(2):139-142.

(MENG Z J, YUE X N, YUAN Z H. Model of causes for urban fog-haze based on multiple regression analysis[J]. Journal of Shenyang University(Natural Science), 2015,27(2):139-142.)

【责任编辑: 李艳】

Multivariate System Fault Diagnosis Methods and its Applications Based on Residual Principal Component Analysis

GaoHui,LiYanping

(Key Laboratory of Manufacturing Industrial Integrated Automation, Shenyang University, Shenyang 110044, China)

Abstract:By establishing a self-regression model of error, a kind of fault diagnosis method is presented for multivariate system by residual weighted principal component analysis. This method can eliminate the self-correlation of error data, and makes up the defects of other principal component analysis. Simulation results of an application example show that the proposed method is effective in fault diagnosis of multivariate system.

Key words:multivariate system; fault diagnosis; error model; residual weighted; principal component analysis

中图分类号:

文献标志码:A

文章编号:2095-5456(2016)02-0141-06

作者简介:高会(1989-),女,河北石家庄人,沈阳大学硕士研究生; 李彦平(1957-),男,辽宁锦州人,沈阳大学教授,博士.

收稿日期:2015-11-03