一种基于安全换道距离规则的对称同向双车道交通流模型

徐洪学, 楚淑芳

(1. 沈阳大学 信息工程学院, 辽宁 沈阳　110044; 2. 营口市卫生学校 数理教研室, 辽宁 营口　115000)



一种基于安全换道距离规则的对称同向双车道交通流模型

徐洪学1, 楚淑芳2

(1. 沈阳大学 信息工程学院, 辽宁 沈阳110044; 2. 营口市卫生学校 数理教研室, 辽宁 营口115000)

摘要:基于对元胞自动机交通流模型STCA与F-STCA的深入研究,结合对称同向双车道车辆驾驶安全换道的实际状况,完善了车辆驾驶过程中的换道风险描述,提出更符合实际情况的对称同向双车道车辆安全换道距离规则及基于该规则的对称同向双车道元胞自动机交通流模型X-STCA.利用MATLAB模拟环境进行仿真实验,结果表明该模型在保证对称同向双车道车辆换道安全的前提下,大大增加了车辆加速换道次数,从而有益于提高车流速度、降低车流密度和减少道路拥堵.从换道安全和改善交通环境角度考虑,该模型更符合对称同向双车道交通流实际情况.

关键词:元胞自动机; 安全换道距离; 对称同向双车道; 交通流

将元胞自动机(Cellular Automata,CA)理论应用到交通流管理系统的先驱是Wolfram.Wolfram于1983年提出了著名的184号规则[1],该规则指出:如果在t时刻,一个元胞及其右侧邻居是黑色的,或者该元胞是白色的,并且其左侧邻居是 黑色的,那么该元胞就会在t+l 时刻变成黑色.作为对Wolfram-l84号规则的应用,Negel和Schreckenberg于1992年提出了NS(Nagel-Schreckenberg)元胞自动机交通流模型[2],NS模型能够清楚表达同向单车道交通流从自由运动到拥挤堵塞的相变情况,具有里程碑意义,但NS模型具有不可超车的局限性.Chowdhury基于NS 模型对NS模型进行扩展,提出了对称同向双车道元胞自动机(Symmetric Two-lane Cellular Automata, STCA)模型[3],该模型的最大特点是引入了比较符合实际 交通流状态的双车道换道规则.

STCA模型依据的换道规则是所有换道车辆应该满足的安全换道距离都是固定不变的,然而在实际车辆驾驶过程中,不 同车辆的行驶状态随时都在发生变化,对所有换道车辆均设定一个固定的安全换道距离并不合适.在分析研究STCA模型 的基础上,王永明提出了弹性安全换道距离的概念和对应的安全换道距离规则,并提出了一种基于该安全换道距离规则的元胞自动机交通流模型(F-STCA)[4-6].该模型考虑了行驶在相邻车道的后车对换道车辆安全方面的影响,能够更好地模拟实 际交通流情况.

但在实际车辆驾驶过程中,驾驶员在决定是否更换车道时,不仅要考虑行驶在相邻车道的后车对换道车辆的影响,也要 考虑行驶在相邻车道的前车对换道车辆的影响.文献[7]关注到了这一问题,并经过分析研究后提出了一种基于改进了的安全换道距离规则的元胞自动机交通流模型,但在该模型中有关换道风险度值的设定仅仅针对了具体的特殊情况,不具有普遍性.

本文基于STCA模型和F-STCA 模型的研究成果,综合考虑了同向双车道系统中换道车辆与相邻同向车道前后车辆之间可能存在的冲突,提出一种更加完善的安全换道距离规则,并提出一种基于该安全换道距离规则的同向双车道元胞自动机交 通流模型.

1STCA模型与F-STCA 模型分析

1.1STCA模型

Chowdhury提出的STCA模型是对NS模型的扩展,其最大特点是引入了符合交通流状态的同向双车道换道距离规则:

(1)

规则中的参数定义为:dn(t)表示时刻t、第n辆车与前方车辆的距离;dn,other(t) 表示时刻t、第n辆车与相邻车道前方车辆的距离;dn,back(t)表示时刻t、第n辆车与相邻车道后方车辆的距离;Cn(t)表示时刻t、第n辆车所在车道,且Cn(t)=1或0;vmax为车道最大限制速度;dsafe表示模型中限定的安全换道距离,为保证安全,设定dsafe=vmax为固定值.

另外,规则中的dn(t)dn(t)表示时刻t受阻挡车辆有可能在相邻车道上达到更快的速度(具有空间可能性);dn,back(t)>dsafe表示换道车辆与相邻车道上后方车辆必须 保持的安全距离,此为换道车辆换道时所需满足的安全换道距离条件.

1.2F-STCA模型

文献[4-6]通过分析STCA模型换道距离规则存在的不足,分别提出符合实际交通流状态的元胞自动机模型:F-STCA-Ⅰ模型和F-STCA-Ⅱ模型.其中,F-STCA-Ⅰ模型对应的换道距离规则描述为

(2)

通常,驾驶人员往往难以准确地判断相邻车道后方车辆的速度(可以通过技术手段实现),只能凭借驾驶经验采用F-STCA-Ⅰ模型.为了进一步提高换道的安全性,文献[6]假设相临车道后方的车辆以最大限制速度vmax前进,则在此假设条件下,换道距离规则进一步改进为

(3)

else

Cn(t+1)=Cn(t).

1.3F-STCA 模型换道距离规则问题分析

文献[7]引用的问题实例,考虑如图1所示元胞自动机换道模型,图中有数字的元胞表示被车辆占据,且数字为车辆速度.

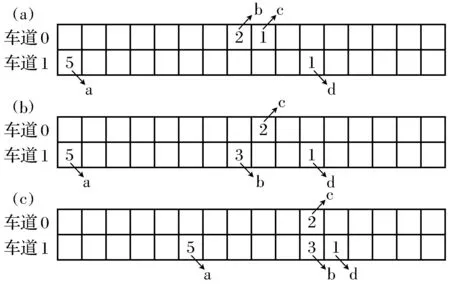
图1　F-STCA模型换道距离规则分析

假设vmax=5,则在t时刻:db(t)=0db(t),db,back(t)=6>dsafe=5,即车辆b遵循STCA模型换道规则;同时db,back(t)=6>1+5-min(vb(t+1),vmax),即该换道情景中车辆b也遵循F-STCA模型弹性换道距离规则,如图1a所示.此时若车辆b和c都在加速,且车辆b实施换道,如图1b所示.则下一步即呈现出如图1c所示的t+1时刻的状态,此刻车辆b将面临着与车辆c或车辆d造成冲突的两难境地:继续加速行驶,可能追尾车辆d;换道行驶,可能与车辆c相撞,除非车辆b放弃加速.

2X-STCA模型

基于上述分析,本文同时考虑同向相邻车道前车及后车对换道车辆可能存在的潜在冲突问题,提出一种符合实际交通流情况的安全换道距离规则.结合道路交通实际情况及讨论问题需要,本文引入vmin作为车道最小限制速度,因而车辆运行速 度满足:vn∈[vmin,vmax].

首先完善文献[6]中提出的换道风险的描述.车辆在换道时具有一定风险,风险主要来自于同向双车道中车辆换道并行驶一个时间步以后,同向相邻车道后方车辆与前方车辆对换道车辆造成的冲突,冲突大小取决于两个要素:①换道车辆与相邻车道后方车辆的距离dδ,back(t+1);②换道车辆与相邻车道前方车辆的距离dδ,other(t+1).

为保证交通安全,令dδ,back(t+1)≥1及dδ,other(t+1)≥1作为换道车辆与相邻车道后方车辆及换道车辆与相邻车道前方车辆之间的缓冲距离约束,并以此推导换道距离规则.

基于dδ,back(t+1)≥1约束得到的换道距离规则及对应的元胞自动机模型如式(2)和式(3)所示,变道微观场景图如图2所示.其推导过程参见文献[6].

本文基于dδ,other(t+1)≥1约束推导F-STCA模型没有涉及到的换道距离规则,并提出一种安全换道距离规则及基于该规则的元胞自动机模型----X-STCA模型.基于dδ,other(t+1)≥1约束的变道微观场景图如图3所示.

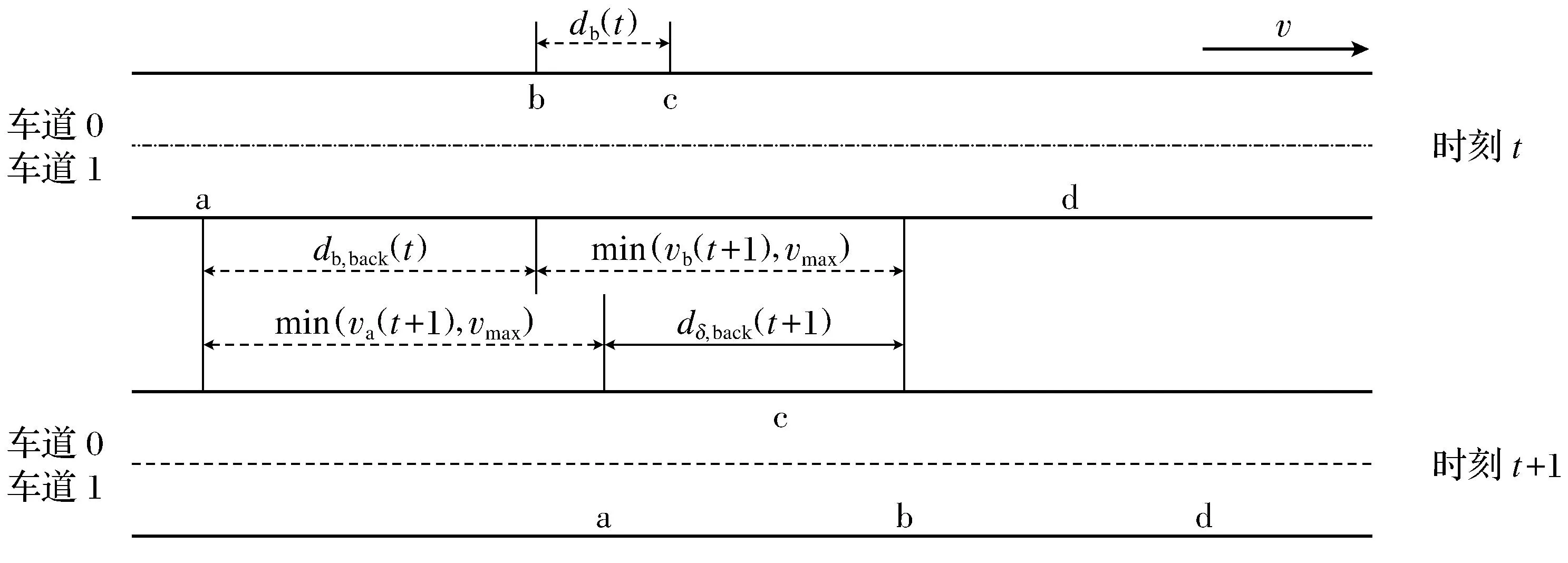
图2　换道情景(dδ,back(t+1)≥1 约束)

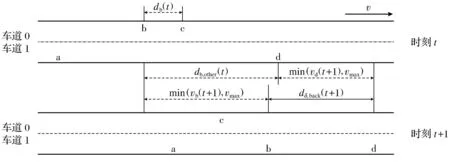
图3　换道情景(dδ,other(t+1)≥1约束)

如图3所示,车辆b在t时刻换道,并且行驶一个时间单位.由图3可知:

(4)

令dδ,other(t+1)≥1,则由式(4)即可得出下面结论:

(5)

由此,可以得到基于dδ,other(t+1)≥1约束的换道距离规则:

(6)

else

Cn(t+1)=Cn(t).

通常,在车辆行驶过程中,驾驶人员往往难以准确判断相邻车道前方和后方车辆的准确速度,只能凭借驾驶经验采用X-TCA模型.为了进一步提高换道安全,假设相临车道后方车辆和前方车辆分别以最大限制速度vmax和最小限制速度vmin前进,则在这个假设条件下,换道距离规则可进一步改进为

if(min(vn(t+1),vmax)>dn(t)and

(7)

else

Cn(t+1)=Cn(t).

3数值模拟及分析

基于MATLAB环境对X-STCA模型进行数值模拟,重点考察车流密度变化与车辆换道次数之间的变化关系,用以比较 式(1)、式(3)及式(7)换道距离规则对应的元胞自动机交通流模型的区别.

设定初始时刻车辆随机分布在同向双车道上,车辆连续运行多个时间步,并有不同速度车辆混合其中,形成多车速混合 车流.定义两条长度L=1 000km的一维离散元胞链表示同向双车道,每个元胞表征实际长度为7.5km,车辆分布在该元 胞链上,即模拟实际长度为7.5km,并采用周期性边界条件,最大限制速度vmax为5个元胞单位/h,最小限制速度vmin为0.

图4为车辆加速换道次数比例与车流密度比例之间的关系图.其中在低密度区[0.05-0.70],X-STCA模型明显高于其他2个模型;而在高密度区[0.7-1.0),三个模型基本重合,表示车流密度过大时,车辆很少换道,形成堵塞区.

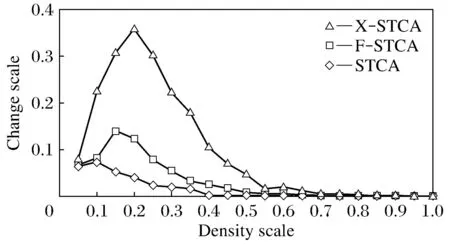
图4　车辆加速换道频度与交通流密度的关系比较

4结论

本文结合车辆安全换道的实际需要,在分析研究STCA与F-STCA模型的基础上,重新定义了换道风险度的概念,提出了基于安全换道距离规则的对称双车道元胞自动机模型X-STCA,并将该模型应用于混合交通流环境中进行了数值模拟与分析.模拟实验结果表明该模型在保证车辆换道安全的前提下,大大增加了同向双车道车辆安全换道的次数,从而有益于提高车流速度、降低车流密度和减少道路拥堵.从换道安全和改善交通环境角度考虑,该模型更符合同向双车道交通实际情况.

参考文献:

[1] WOLFRAM S. Statistical mechanics of cellular automata[J]. Reviews of Modern Physics. 1983,55(3):601-644.

[2] NAGEL K, SCHRECKENBERG M. A cellular automaton model for freeway traffic[J]. Journal of Physics I France, 1992,2(12):2221-2229.

[3] CHOWDHURY D, WOLF D E, SCHRECHENBERG M. Particle hopping models for two-lane traffic with two kinds of vehicles: effects of lane-changing rules[J]. Physica A: Statistical Mechanics and its Applications, 1997,235(3/4):417-439.

[4] 王永明,周磊山,吕永波. 基于元胞自动机交通流模型的车辆换道规则[J]. 中国公路学报, 2008,21(1):89-93.

(WANG Y M, ZHOU L S, LYU Y B. Lane changing rules based on cellular automaton traffic flow model[J]. China Journal of Highway and Transport, 2008,21(1):89-93.)

[5] 王永明,周磊山,吕永波. 基于弹性安全换道间距的元胞自动机交通流模型[J]. 系统仿真学报, 2008,20(5):1159-1162.

(WANG Y M, ZHOU L S, LYU Y B. Cellular automaton traffic flow model considering flexible safe space for lane-changing[J]. Journal of System Simulation, 2008,20(5):1159-1162.)

[6] 王永明. 非常态事件影响下的交通组织规划及交通流模拟研究[D]. 北京:北京交通大学, 2009.

( WANG Y M. Studies on traffic organization planning and traffic flow simulation under the influence of major public emergencies[D]. Beijing: Beijing Jiaotong University, 2009.)

[7] 徐洪学,张冬梅. 一种基于改进的弹性安全换道间距规则的元胞自动机模型[J]. 沈阳大学学报(自然科学版), 2014,26(5):369-371.

(XU H X, ZHANG D M. A cellular automaton model based on improved rules of flexible safe lane changing distance[J]. Journal of Shenyang University (Natural Science), 2014,26(5):369-371.)

【责任编辑: 肖景魁】

A Symmetric Same Direction Two-Lane Traffic Flow Model Based on Safe Lane Changing Distance Rule

XuHongxue1,ChuShufang2

(1. School of Information Engineering, Shenyang University, Shenyang 110044, China; 2. Teaching and Research Office of Mathematics and Physics, Yingkou Hygiene School, Yingkou 115000, China)

Abstract:Based on the further research of STCA and F-STCA cellular automata traffic flow model, combined with the actual situation of the symmetric same direction two-lane safe lane changing, improve the description of symmetric same direction two-lane safe lane changing risk, the symmetric same direction two-lane safe lane changing distance rule and cellular automata traffic flow model are proposed, which are more in line with the actual situation. The simulation experiment has been done based on the MATLAB simulation environment, the experimental results show that the model can greatly increasing the frequency of vehicle acceleration and lane changing, which is beneficial to the improvement of traffic speed, reduce the density of traffic flow and reduce road congestion, under the premise of ensuring the symmetric same direction two-lane safe lane changing. Considered from the safe lane changing and improve traffic environment point of view, the model is more conform to the actual situation of the symmetric same direction two-lane traffic.

Key words:cellular automata; safe lane changing distance; symmetric same direction two-lane; traffic flow

中图分类号:U 491; TP 391

文献标志码:A

文章编号:2095-5456(2016)02-0118-04

作者简介:徐洪学(1962-),男,辽宁大连人,沈阳大学教授,博士.

基金项目:国家“十二五”支撑计划资助项目(2011BAJ06B04).

收稿日期:2015-09-30