基于HHT的人员及车辆震动信号联合去噪方法

赵春晖, 王　杨, 唐胜武,2

(1. 哈尔滨工程大学 信息与通信工程学院, 黑龙江 哈尔滨　150001;

2. 中国电子科技集团公司 第四十九研究所, 黑龙江 哈尔滨　150001)



基于HHT的人员及车辆震动信号联合去噪方法

赵春晖1, 王杨1, 唐胜武1,2

(1. 哈尔滨工程大学 信息与通信工程学院, 黑龙江 哈尔滨150001;

2. 中国电子科技集团公司 第四十九研究所, 黑龙江 哈尔滨150001)

摘要:提出了一种基于HHT的FCL(分型守恒定律,Fractal Conservation Law)与小波动态阈值联合去噪的方法.该方法将原始的人、车震动信号经过HHT分解后得到该震动信号的不同频率分量.对低频信号部分,采用FCL算法进行去噪,对去噪后的各个低频信号进行重组;对高频信号部分,采用小波动态阈值滤波去噪并重组高频信号.将重组后的高、低频信号进行求和得到降噪后信号.

关键词:固有模态函数; 黄-希尔伯特变换; 分型守恒定律; 小波动态阈值

战场环境中,由于背景噪声等外界条件的影响,人员、车辆等产生的地震动信息往往会受到干扰,难以分辨识别,这类地震动信号属于典型的非平稳信号[1].目前对人员、车辆产生的地震动信号处理的主要方法有傅里叶变换[2-3]、Gabor变换[4]、小波变换[5-7]等.其中,傅里叶变换由于缺乏时间的局部信息,既无法告知某些频率成分发生在哪些时间内,也无法表示某个时刻信号频谱的分布情况,所以它只适用于确定性信号及平稳信号分析.而对时变信号、非平稳信号该方法则无法处理.Gabor变换本质属于加窗傅里叶变换,对于Gabor变换,其时频窗口大小、形状不变,只有位置变化。而实际应用中常常希望时频窗口的大小、形状能够随频率的变化而变化,这就使Gabor变换存在一定的缺陷.而且其计算量较大,有时还可能产生吉普斯现象.

HHT是一种处理非线性信号的方法[8-10].HHT算法的核心是对信号进行EMD(经验模态分解,Empirical Mode Decomposition)分解,通过EMD分解可得到各个不同频率的IMF分量.其中得到的不同IMF分量都是稳定的非线性信号.该方法在分解过程,依据数据本身的时间尺度特征,能够保留数据本身的特性,进而实现信号特征的量化提取[11].同傅里叶变换、Gabor变换相比,HHT具有较好的客观性和自适应性,并能够更好地反应一个信号的非线性特性.因此,HHT适用于非线性和非平稳动态变化的地震动信号的处理.

1998年,N.E. Huang等学者提出了HHT理论,该理论是非线性、非稳定信号分析处理领域的全新方法[12].该方法从根本上克服了傅里叶变换的局限性,是一种更具适应性的时频局部化分析方法[13].由于HHT存在有效信息丢失等问题,后人对其不断地改进.吴甄非等人于2011年提出基于HHT的人员脚步信号识别算法[14];林振华等人于2014年提出基于HHT的车辆震动信号分类方法[15];2015年,杨大为提出了基于HHT方法的小波阈值降噪滤波方法,对HHT方法处理过程中由EMD分解出的半数的IMF分量单独进行小波阈值滤波处理[16].该方法有效地改进了HHT在信号降噪处理中丢失有效信号的问题,但存在噪声处理不彻底等问题.

本文针对HHT方法的信息丢失、去噪不彻底等问题,提出了一种基于HHT的FCL与小波联合去噪方法.该方法针对HHT分解后的人、车震动信号的高、低频率分别进行小波动态阈值去噪及FCL去噪,并对去噪后的震动信号进行重组,较大程度地保留了人、车信号信息,同时达到了噪声滤除的效果.

1希尔伯特-黄变换(HHT)理论

HHT理论主要包括EMD及希尔伯特变换两个部分.

1.1经验模态分解

HHT又叫做EMD.利用EMD分解把时间序列函数分解成若干个具有实际物理意义的固有模态函数序列,而后对分解得到的各个不同频率分量进行希尔伯特变换获取这些序列的时频谱,即Hilbert谱.

HHT的核心是EMD.EMD将原始信号分解成有限个IMF分量,其中IMF需满足以下两个约束条件:

(1) 在整个信号长度内,极值点数目和过零点的个数必须相等或最多只差一个;

(2) 在任意时刻内,由极大值点和极小值点组成的上、下包络线的平均值为0,即上、下包络线关于时间轴是对称的.

EMD方法分解信号过程如下:

步骤1设原始时间序列的信号函数为x(t),求出原信号x(t)的极大值和极小值.采用三次样条函数插值法,获取信号的上包络序列值和下包络序列值,分别记作xmax(t)和xmin(t).对每一个序列的xmax(t)和xmin(t)求取平均值m1(t);

步骤2求出信号x(t)上、下包络线的均值记作m1(t),计算原信号x(t)与均值m1(t)的差值:

(1)

依据IMF分量的两个约束条件来判断h1是否是一个IMF分量.若满足条件,则h1为原始信号的第一个IMF分量.

步骤3如果h1不满足IMF条件,则把h1作为原始信号,重复步骤1和步骤2.得到新的上下包络平均值m11,同时求出h11=h1-m11,再继续判断h11是否满足IMF的约束条件.若仍不满足,继续循环计算k次,直到h1k满足条件停止,计算差值h1k=h1(k-1)-m1k.同时令C1(t)=h1k(t).

步骤4把c1(t)从用原始信号x(t)中去除得剩余信号:

(2)

步骤5把剩余信号r1(t)重新进行以上步骤的筛选,可得到信号x(t)的若干个固有模态函数,记ci(t),i=1,2,…,n和一个剩余量rn(t),当rn(t)为一个单调函数时,循环停止,即有:

(3)

式(3)中ci(t)是各个IMF分量,rn(t)为残余函数.所分解出的IMF突出了原信号的局部特征信息.

1.2希尔伯特变换

经过经验模态分解后得到若干个固有模态函数IMF后,分别对IMF进行希尔伯特变换,即得到每个分量的瞬时频率谱,把所有的IMF的瞬时频谱求和就可以得到原信号的Hilbert谱.

Hilbert变换过程如下:分别对每一个经EMD分解后得到的各阶IMF分量作Hilbert变换得:

(4)

构造解析信号:

(5)

其中,信号幅值为

(6)

相位为

(7)

IMF的瞬时频率定义:

(8)

则原信号x(t)可表示为

(9)

2基于HHT的FCL与小波联合去噪方法

文献[16]提出的基于HHT的小波动态阈值去噪方法仅仅是对前N/2个IMF分量单独进行小波阈值滤波降噪处理,而对于后N/2个低频分量未做任何去噪的处理.在实际人、车震动信号中,低频分量内仍含有许多干扰噪声,会对结果造成一定的影响.为了更准确有效的去除噪声,获得更纯净的原始信号,本文提出一种基于HHT的FCL与小波动态阈值联合去噪方法.

2.1分型守恒定律FCL

FCL算法源于Fowler AC等人所研究的方程模型[17]:

(10)

其中I是一个非局部算子,定义为

(11)

2012年,Azerad将式(11)修改成如下方程:

(12)

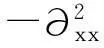
将式(12)应用于震动信号处理时,x和t将不再具有空间和时间的数学意义.这里的x表示数据的采样点数,而t则仅是一个参数.u=u(t,x)是滤波后的信号,u0表示所获得的初始含噪信号,T代表任意正时间量,a和b是正常数,Iλ是分数阶算子,当λ∈(1,2)时,Iλ定义为:

(13)

因为ε只是一个被积符号,所以式(12)中用“·”来代替.αλ是一个适当的常量.

综上所述，饮食护理应用于精神分裂症并2型糖尿病患者中，可更好对患者的血糖水平控制，且可提高其对护理服务的满意程度，以此提高精神分裂症并2型糖尿病患者的生活质量，改善其预后。

由以上分析可以看出,经过修改后的方程(12)的建立是该算法的核心.

2.2小波动态阈值算法

设含噪的地震动信号为

(14)

式中xk(t)是有效信号,nk(t)为随机噪声.在本文中xk(t)是EMD分解后的第k个IMF分量,即xk(t)=ci(t).对信号做离散小波变换,得到小波系数Wf(j,t),这里记作wj,t=Wf(j,t).对xk(t)=sk(t)+nk(t)做离散小波变换后,得到的小波系数由两部分组成:一部分是信号sk(t)对应的小波系数Ws(j,t),一部分是噪声信号nk(t)对应的小波系数Wn(j,t).最后选取适当的阈值函数对小波变换系数进行处理.

具体方法如下:

① 将提取到的含噪原始信号经EMD分解获取若干个IMF分量x1(t),x2(t),…,xn(t);

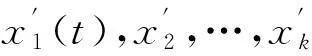
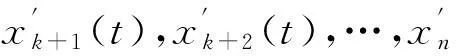
④ 重构高频分量f1(t)和低频分量f2(t)得到去噪后的纯净信号:f(t)=f1(t)+f2(t).

算法流程图如图1所示.

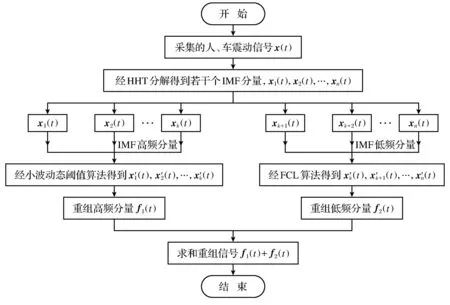
图1　算法流程图

3MATLAB实验仿真与结果分析

本文针对人、车产生的震动信号进行去噪研究,提出了一种基于HHT的FCL和小波动态阈值联合去噪的方法.试验中采用两组数据进行验证,分别对车辆震动信号和人员脚步信号采用HHT滤波法、基于HHT的小波动态阈值去噪法以及本文的基于HHT的FCL与小波动态阈值联合去噪法进行对比验证.

3.1车辆震动信号数据仿真与分析

本实验的信号来自某广阔操场上的车辆,含有非目标车辆、人员等外界干扰,测试环境较为复杂.信号是由埋设在地表下的磁电式震动传感器探测得到,采样频率为1 kHz,并将传感器探测得到的信号经过调理转换电路处理得到原始信号,如图2所示.

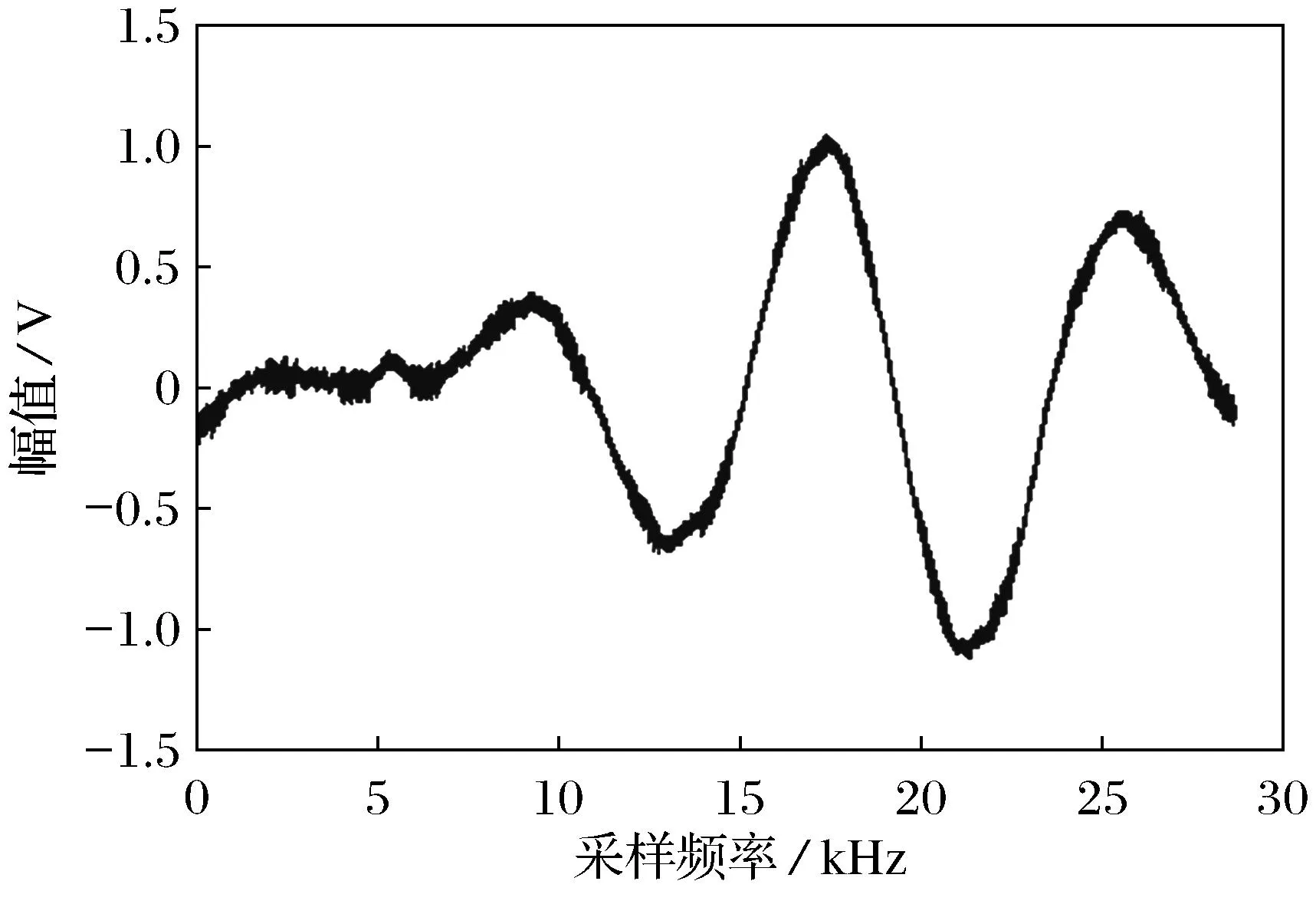
图2　原始信号

由HHT可知,任何信号可以由EMD分解得到若干个不同频率的分量.把各个频率的IMF分量进行分析、筛选、滤波、重组得到的新的信号即去噪后的信号.

从图3～图5中可以看出,对于车辆产生的地震动信号,其噪声主要出现在高频分量部分,采用HHT方法对原始信号进行分解得到12个不同频率的的IMF分量.将IMF1、 IMF2、 IMF3、IMF4滤除掉,同时将剩余的8个IMF分量进行重组达到对原始信号降噪的目的.

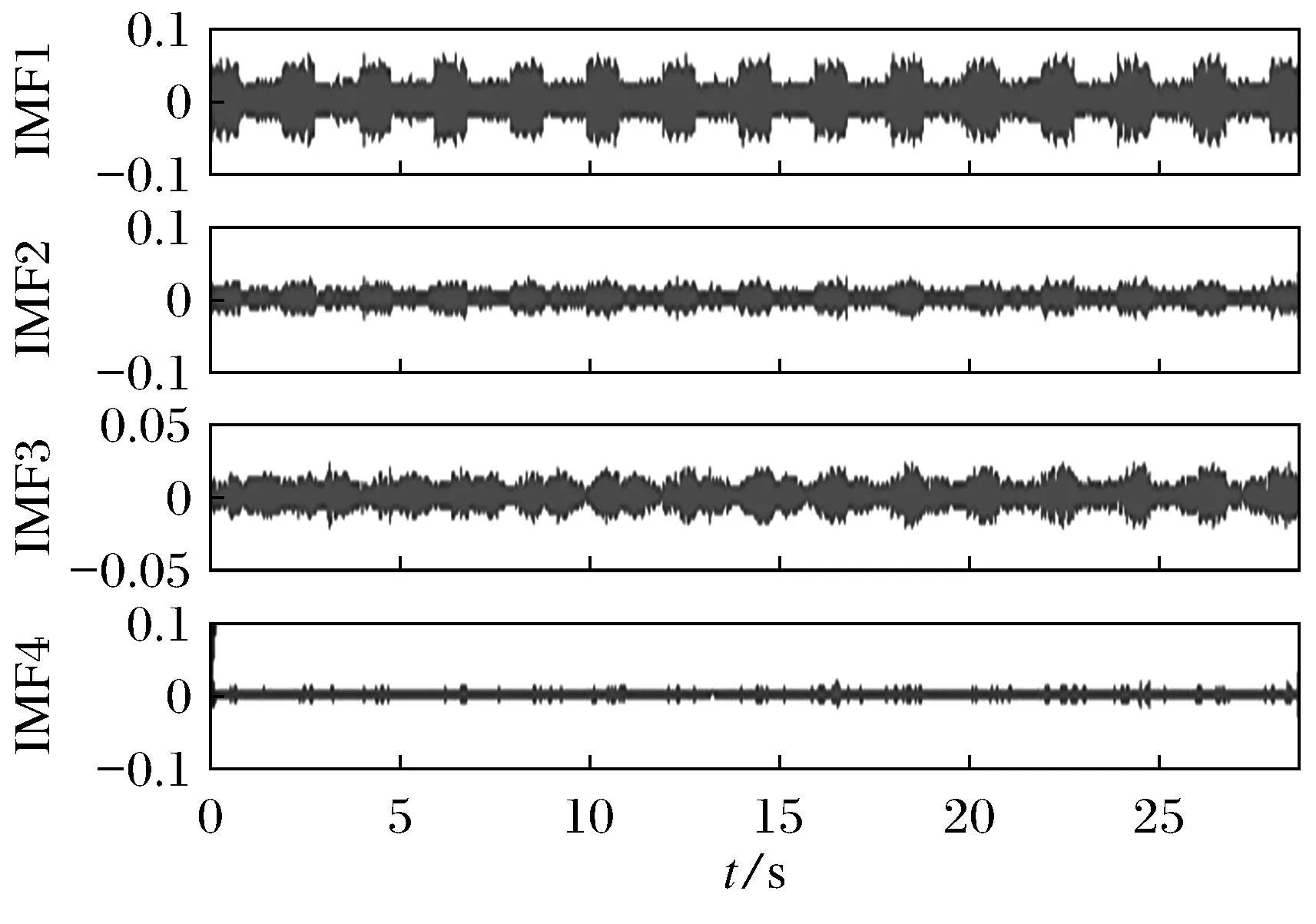
图3　经EMD分解后的IMF1～IMF4分量

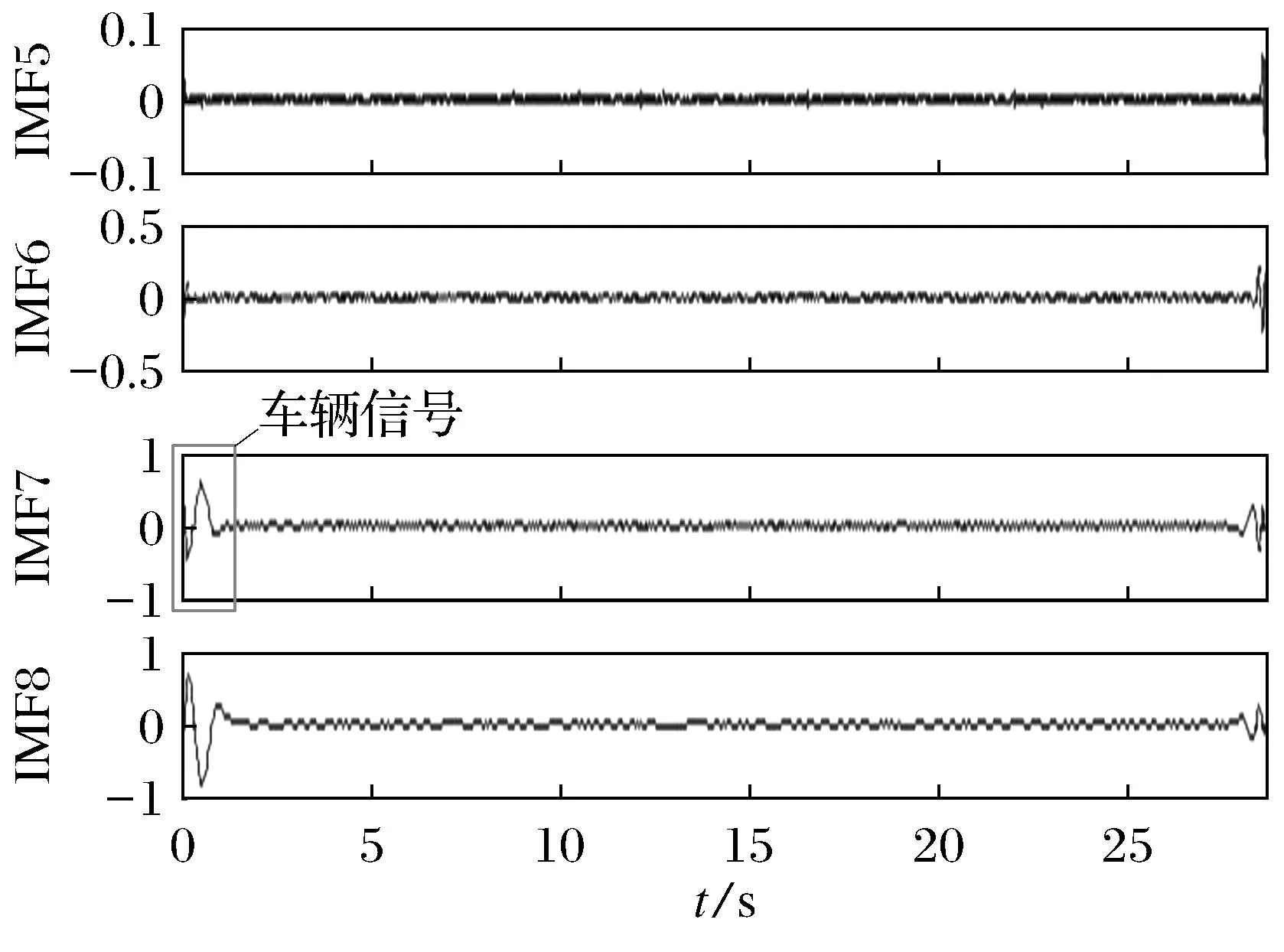
图4　经EMD分解后的IMF5～IMF8分量

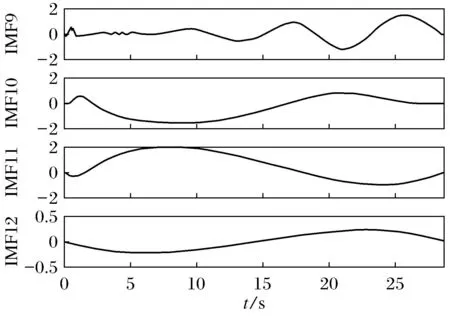
图5　经EMD分解后的IMF9～IMF12分量

从图6b可以看出,含有噪声的原始信号经过HHT滤波后达到了去噪的目的,但是去噪效果十分不明显.在对信号进行HHT滤波降噪的整个过程中,将前4个高频分量直接滤除,对剩余8个分量进行求和重组.尽管这个方法可以达到降噪的目的,但是在前4个分量中会包含原始信号的部分信息,这样就会出现有效信息丢失的严重问题.2015年杨大为等人又提出了一种基于HHT的小波动态阈值滤波法对信号进行去噪.

图6c分别对前N/2个IMF分量采用小波动态阈值滤波处理,之后与剩余后N/2个分量重组,即得到基于HHT的动态阈值去噪结果.与HHT滤波方法相比,这种对信号去噪的方法不仅有效地改善了HHT滤波过程中信号有效信息丢失的问题,同时还使去噪后信号更加平滑,去噪效果也更加明显.

为了得到更纯净的信号,图6d将采集到的原始信号通过HHT算法分解得到了12个IMF分量,将高频分量通过小波动态阈值去噪后重构出新的高频信号分量.对其余低频分量采用FCL算法滤波去噪后重构得到了新的低频分量.将新的高频分量与低频分量加权求和重构得到去噪后信号.通过实验可以看出,基于HHT的FCL与小波动态阈值联合去噪法对噪声的滤除效果更佳,可以得到更纯净的信号,同时也避免了有效信息丢失的问题,为后续目标检测、识别等工作降低了难度,具有重要的意义.

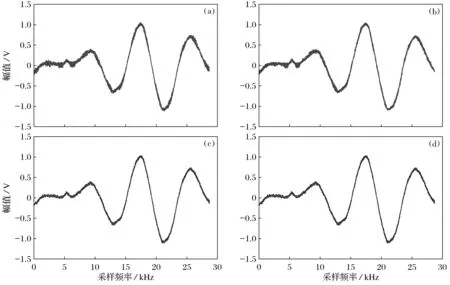
图6　车辆信号去噪图

3.2人员震动信号数据仿真与分析

实验3.2中的原始信号为在广阔的操场上采集到的人走路产生的地震动信号,采样频率为2 kHz.由于在一般情况下人员脚步频率约为2 Hz,因此在实际应用中每0.5 s处理一次信号.

图7a为原始信号,图7b为经HHT滤波后信号,图7c为HHT分解后的小波动态阈值去噪后的信号,图7d为基于HHT的FCL与小波联合去噪后的信号.从实验的结果对比图清楚的看出,图7d这种联合去噪的效果明显优于前三种方法,可以得到更纯净的人员脚步信号,噪声去除的更加彻底,同时也验证了本文提出方法的可行性.

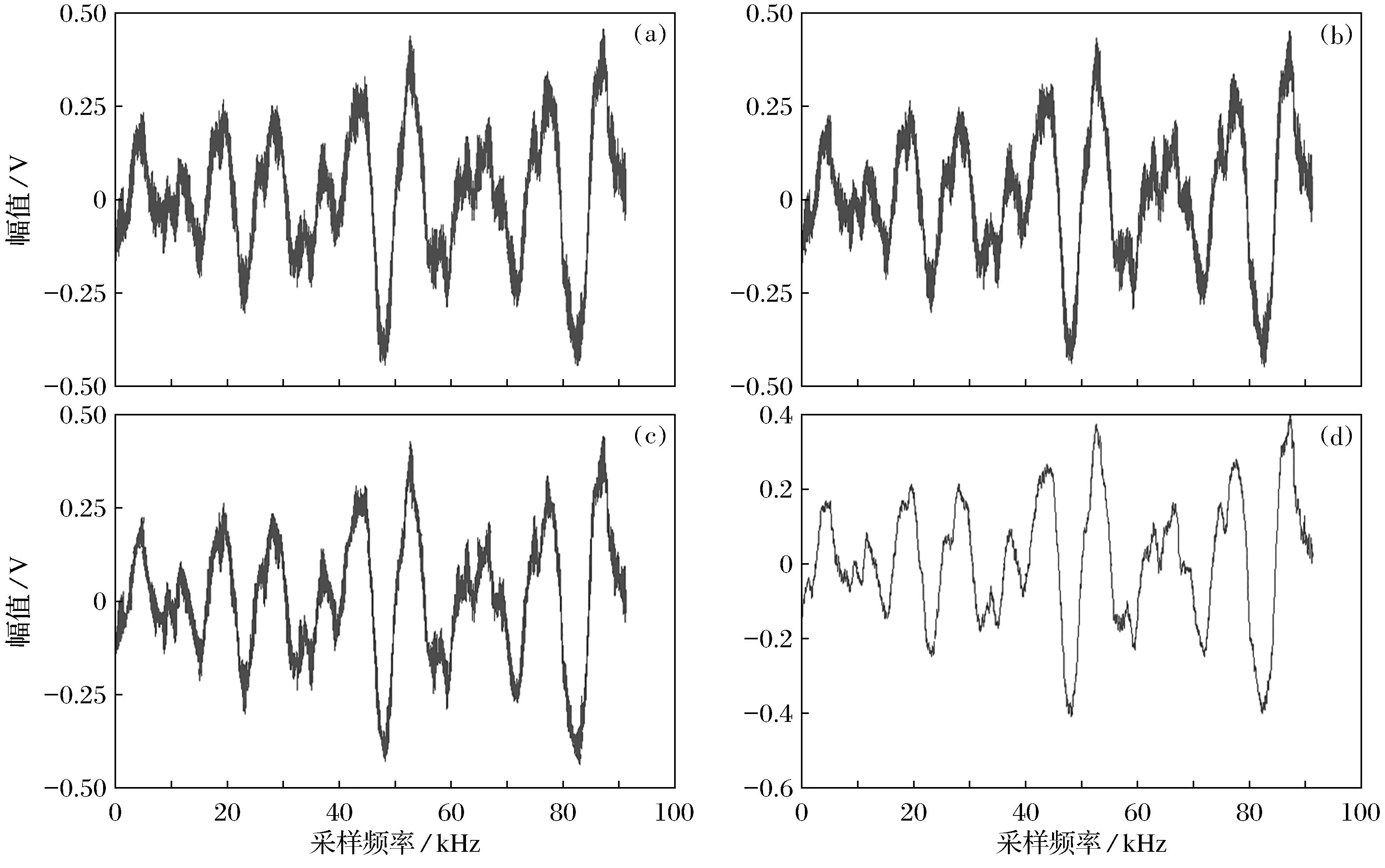
图7　人员信号去噪图

为了有一个更好的量化结果,同时为了验证本文算法的可行性与实际应用性能,针对实验3.2我们采集了不同噪声下的人员脚步震动信号.估算HHT滤波去噪后信号、基于HHT的小波动态阈值去噪后信号以及基于HHT的FCL与小波联合去噪后信号的信噪比,如表1所示.信噪比估算公式为[18]:

(16)

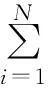
从表1可以看出,本文提出方法的信噪比与前两种方法相比有大幅度的提高.

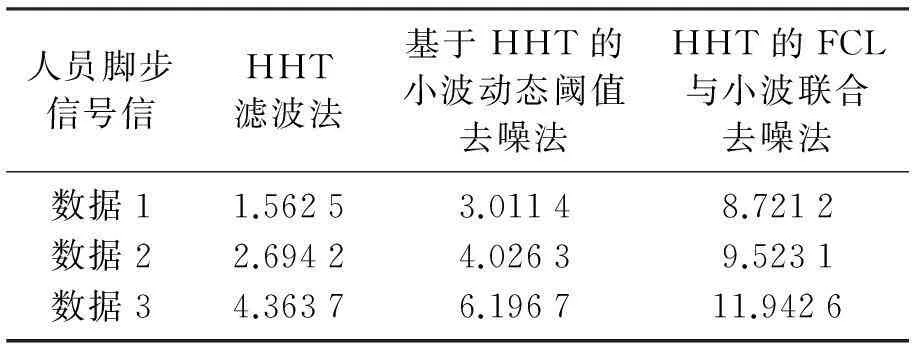
表1　性能评估比较

4结论

本文提出一种基于HHT基于的FCL与小波联合去噪法.在HHT分解信号之后,对高频、低频分量分别进行小波动态阈值去噪和FCL去噪,而后对信号进行求和重组.这个新方法不仅解决了HHT滤波对信号有效信息丢失的问题,同时还改善了基于HHT的小波动态阈值法去噪不彻底的问题.通过对地面的人、车产生的震动信号进行实验,验证了该方法的可行性.但由于该方法是将三种算法联合进行去噪,所以在对信号处理的效率和时间上有一定的影响,有待进一步研究改善.

参考文献:

[1] 朱维,靳平,陶良小,等. 车辆目标地面振动信号的识别技术研究[G]∥国家安全地球物理丛书(七)----地球物理与核探测, 2011:7.

(ZHU W, JIN P, TAO L X, et al. The seismic signal based target recognition of moving vehicles[G]∥National security geophysical series(Seven)—Geophysical and nuclear detection, 2011:7.)

[2] HU G S. Digital signal processing theory, algorithm and implementation[M]. Beijing: Tsinghua University Press, 1997.

[3] ZHENG Z Z. Digital signal processing basis[M]. Beijing: Seismological Press, 1998.

[4] WEXLER R. Discrete Gabor expansions[J]. Signal Processing, 1990,21(3):207-221.

[5] YIN J Y, ZHU Y Q, SONG Z P, et a1, Hundred-year-scale cycle of seismic activities in western China and its negative correlativity with sunspot activity[J]. Chinese Journal of Geophysics, 201l,54(9):2263-2271.

[6] DAUBECHIES I. Orthogonal bases of compactly supported wavelets[J]. Communication Pure and Application Mathematics, 1988,41:909-996.

[7] MALLAT S G. Multifrequency channel decompositions of images and wavelet models[J]. IEEE Trans ASSP, 1989,37(12):2091-2110.

[8] HUANG N E, WU Z. A review on Hilbert Huang Transform: method and its applications to geophysical studies[J]. Reviews of Geophysics, 2008,47(2):1-23.

[9] WU A X, WU P Z, XU P. Empirical mode decomposition, data emulation and test of deformation signal filtering[J]. Earthquake, 2007,27(3):20-25.

[10] ZHOU Z, SHAN X M, ZHANG L, et a1. The gravity tide of Kunming & Xiaguan based on the HHT[J]. Chinese Journal of Geophysics, 2008,51(3):836-844.

[11] WU A. HHT time-frequency analysis of digital seismic waveform signals[C]∥2012 9th International Conference on Fuzzy Systems and Knowledge Discovery, May 29-31, 2012:1802-1806.

[12] 吴俊,张榆锋. 经验模态分解和小波分解滤波特性的比较研究[J].云南大学学报(自然科学版), 2012(3):285-290.

(WU J, ZHANG Y F. The differences analysis on filtering properties of empirical mode decomposition and wavelet decomposition[J]. Journal of Yunnan University(Natural Sciences Edition), 2012(3):285-290.)

[13] 李夕兵,张义平,左宇军,等. 岩石爆破振动信号的EMD滤波与消噪[J]. 中南大学学报(自然科学版), 2006(1):150-154.

(LI X B, ZHANG Y P, ZUO Y J, et al. Filtering and denoising of rock blasting vibration signal with EMD[J]. Journal of Central South University (Science and Technology), 2006(1):150-154.)

[14] 吴甄非,余志军,刘海涛. 基于HHT的人员脚步信号识别算法[J]. 计算机工程, 2011,19:168-170,173.

(WU Z F, YU Z J, LIU H T. Human footstep signal identification algorithm based on Hilbert-Huang Transform[J]. Computer Engineer, 2011,19:168-170,173.)

[15] 林振华,李宝清,魏建明,等. 基于震动信号HHT的车辆分类[J]. 计算机仿真, 2010,3:281-285.

(LIN Z H, LI B Q, WEI J M, et al. Hilbert-Huang Transform based on vibrating signal for vehicle classification[J]. Computer Simulation, 2010(3):281-285.)

[16] 杨大为. 基于加速度传感器的HHT信号降噪方法[J]. 仪表技术与传感器, 2015(5):84-85.

(YANG D W. Method of HHT signal noise reduction based on acceleration sensor[J]. Instrument Technique and Sensor, 2015(5):84-85.)

[17] 孟繁磊,李月,杨宝俊. 分形守恒定律在地震数据去噪与增强上的应用[J]. 地球物理学进展, 2015(2):559-564.

(MENG F L, LI Y, YANG B J. Application of fractal conservation law in the simultaneous denoising and enhancement of seismic data[J]. Progress in Geophysics, 2015(2):559-564.)

[18] 王红玲,詹毅,张朝霞. 地震资料信噪比估算法改进[J]. 物探化探计算技术, 2007(3):189-192.

(WANG H L, ZHAN Y, ZHANG Z X. Improvement of signal to noise ratio estimation of seismic data[J]. Computing Techniques for Geophysical and Geochemical Exploration, 2007(3):189-192.)

【责任编辑: 曹一萍】

Combined Method of People and Vehicles Vibration Signal Denoising Based on Hilbert-Huang Transform

ZhaoChunhui1,WangYang1,TangShengwu1,2

(1. College of Information and Communication Engineering, Harbin Engineering University, Harbin 150001, China;2. 49thResearch Institute, China Electronic Technology Group Corporation, Harbin 150001, China)

Abstract:A combined method of signal denoising based on HHT is presented. In this method, the different frequency components of the vibration signal are obtained by the HHT. The low frequency signals are used FCL (Fractal Conservation Law) algorithm for denoising before recombining signals. At the same time, high frequency IMF components are carried on the wavelet dynamic threshold for denoising, and then recombine the IMF components to complete the original signal filter processing.

Key words:IMF; HHT; FCL; wavelet dynamic threshold

中图分类号:TP 216

文献标志码:A

文章编号:2095-5456(2016)02-0111-07

作者简介:赵春晖(1965-),男,黑龙江汤原人,哈尔滨工程大学教授,博士生导师.

基金项目:国家自然科学基金资助项目(61571145, 61405041); 黑龙江省自然科学基金资助项目(ZD201216); 哈尔滨市优秀学科带头人基金资助项目(RC2013XK009003).

收稿日期:2015-11-09