等腰直角三角形螺旋流道内湍流流体流动性能模拟

刘胜举，　王翠华，　吴剑华,　王润康

(沈阳化工大学 能源与动力工程学院， 辽宁 沈阳 110142)



等腰直角三角形螺旋流道内湍流流体流动性能模拟

刘胜举，王翠华，吴剑华,王润康

(沈阳化工大学 能源与动力工程学院， 辽宁 沈阳 110142)

摘要:应用CFD软件研究等腰直角三角形螺旋流道内湍流流体流动特性，计算并对比不同结构参数的数值模型充分发展的湍流流场结构，得出流道内、外壁面的局部阻力系数分布，并分析雷诺数(Re)、曲率及挠率对流体流动阻力的影响.结果表明：等腰直角三角形螺旋流道内湍流流体的二次流为稳定的两涡结构，离心力的作用使外壁面处流体轴向速度梯度远大于内壁面处，因此外壁面的平均阻力系数较大，外壁面的平均阻力系数约为内壁面的1.5～1.7倍.壁面流体平均阻力系数随Re和无量纲曲率的增大而增大，但受挠率影响不大.

关键词：螺旋流道；三角形截面；二次流；湍流流动

作为非圆形截面流道中的一种，三角形截面流道包括三角形直管流道和三角形曲线流道.对三角形直管流道内流体流动的研究文献较丰富，比如Cope[1]和沃林[2]分别对等腰直角三角形截面直管流道中的过渡流动及入口段流动特性进行了实验研究.Abdel[3]用数值模拟分析了充分发展的层流流动下的任意三角形截面管道的流动与换热.祝世兴[4-5]对等腰三角形截面管道入口段及任意三角形管道层流入口段的流动阻力进行了理论分析，并与实验进行了对比，提出了任意顶角三角形长直均匀管道层流进口段速度模型和进口段长度计算公式.Ray[6]运用数值方法研究了恒壁温和恒定热流密度两种边界条件下等边三角形截面直管流道内充分发展层流流体的流动与换热性能.

三角形曲线流道内流体流动性能研究主要涉及三角形弯管流道和三角形螺旋流道两种流道形式.Collins[7-8]用数值方法研究了等腰直角三角形截面弯管流道内稳态流动的性能及截面直角和45°角处的黏性涡的特点.Nandakumar[9]分析了内壁直边和外壁直边两种结构下等边三角形弯管流道内层流流体的流动性能，发现当外壁为直边时，Dean数增大到一定值时层流流体的二次流会出现四涡结构.王翠华等[10-11]对等腰直角三角形螺旋流道层流流体的流动及换热性能进行了数值模拟，但文章中并没有涉及流体的湍流状态，对内、外壁面处流体阻力系数的分布也并未给出细致的分析.由于流体在实际流道内流动时多以湍流形态存在，因此，本文基于三角形螺旋流道的数学模型，采用CFD模拟得到了充分发展条件下不同曲率时的速度场和湍动能分布，比较了外壁面和内壁面处局部阻力系数的大小，分析了Re、曲率和挠率对流道内湍流流体流动阻力的影响.

1数值模拟

1.1物理模型及坐标系统

等腰直角三角形螺旋流道的物理模型及坐标系统如图1所示.其中，Rc为螺旋管道的曲率半径，H为螺距，a为直角三角形斜边的边长.(r,θ,z)为螺旋流道所在的柱坐标系，其时均速度分量分别用vr,vθ,vz来表示.(x,y,s)为正交螺旋坐标系，其时均速度分量分别为u,v,w.

图1　三角形螺旋流道物理模型和坐标系统

1.2数值模拟方法及结果验证

以Fuent 6.3为计算平台，选用RNG κ-ε湍流模型，工作介质采用水(物性参数取300 K时水的参数)，采用无滑移边界，均匀质量流量入口，出口设为充分发展出口，初始湍流强度按Iinlet=0.16Re-1/8估算.计算网格采用非结构六面体网格，各模型网格数量均大于150万，网格划分如图2所示.压力和速度的耦合采用SIMPLEC算法，二阶压力离散，动量、湍动能及湍流耗散率方程均采用二阶迎风离散，收敛残差均取小于1.0×10-6.

图2　流道的网格划分

1.3速度转换及无量纲参数定义

根据柱坐标系和正交螺旋坐标系的关系[13]，u,v,w可用vr,vθ,vz表示为：

w=-sinφcosαvr+cosφcosαvθ+sinαvz;

u=-cosφvr-sinφvθ;

v=sinφsinαvr-cosφsinαvθ+cosαvz.

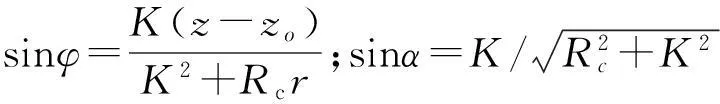
式中：K=H/2π,为绕螺旋线单位弧度时z方向上升高度;α为螺旋线升角;φ为沿螺旋通道中心线极角;zo为横截面斜边中点的z坐标值.

定义以下无量纲参数：

(x′,y′)=(x,y)/dh;w′=w/wm;

(u′,v′)=ρ(u,v)dh/μ.

定义无量纲曲率、无量纲挠率、雷诺数及无量纲涡量ω分别为：

Re=dhwmρ/μ；ω=∂v′/∂x′-∂u′/∂y′.

局部阻力系数为：

fRelocal=2δw,local/(μwm/dh).

平均阻力系数为：

其中:δw,local为壁面的局部切应力;Aw为壁面面积[12].

2模拟结果及分析

模拟计算Re=10 000～20 000，κ=0.1～0.2，τ=0.006～0.02范围内的不同模型，图3给出了κ=0.1,Re分别为12 000，16 000和20 000 时流道横截面上的无量纲轴向速度等值线图、二次流矢量图及无量纲涡量的等值线图(从左至右).由图3可见:湍流流体在三角形螺旋流道内流动时，由于离心力的作用，轴向速度的最大值向外壁面偏移，致使两外直角壁侧的w′等值线密集，其速度梯度远大于内壁侧，横截面上的二次流为旋转方向相反且稳定的两涡结构.随着Re的增大，w′等值线形状基本不变，其最大值的数值逐渐减小.二次涡的结构形态变化不明显，但两涡中心处最大二次流涡量数值明显增大，说明随着Re增大致使二次流动增强.

湍动能是用来表示湍流流动中脉动速度强弱的物理量.图4给出了不同Re值时，湍动能在横截面上的分布云图.从图4中可见:湍动能的最大值集中在靠近壁面附近的区域，并且截面两外壁侧靠近壁面处的湍动能要明显大于截面内壁面侧的湍动能.随着Re的增大，截面上湍动能数值逐渐增大，说明流体脉动速度增强.

图3　κ=0.1、τ=0.006时充分发展湍流流场

图5和图6分别给出了Re和κ变化时外壁面和内壁面上局部阻力系数fRelocal沿y′的分布曲线.从图5和图6可以看出:当κ和Re取定值时，内壁面上的局部阻力系数关于y′=0点基本对称.受上、下二次涡的影响，在接近上、下二次涡中心位置的内壁面处，轴向速度梯度最大，出现内侧壁面fRelocal的峰值.虽然上、下两外壁面的局部阻力系数也关于y′=0点基本对称，但外壁面fRelocal随y′变化的曲线形状与内壁面的大不相同.由于90°顶角处流体的轴向主流速度梯度、二次流速度很小，在所研究的Re范围内，90°顶角的fRelocal还不到外壁面fRelocal峰值的50 %.受离心力及外壁面结构的影响，外侧壁面靠近90°顶角两侧，出现最大轴向速度梯度，因此该两点出现外侧壁面fRelocal的最大值.靠近上、下两45°角顶点附近，其轴向主流速度梯度、二次流速度及湍流脉动速度均很小，所以在上、下两45°角顶点处出现了fRelocal的最小值.

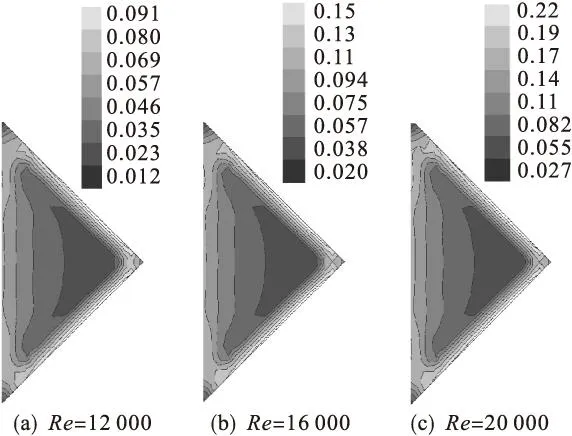
图4　κ=0.1、τ=0.006时湍动能的等值线

具有相同y′值时的内壁面和外壁面相比，除去邻近y′=0和y′=±1.207的边界外，其他外壁面的fRelocal远大于内壁面的fRelocal.经计算得出：在所研究的范围内，外壁面的平均阻力系数约为内壁面的平均阻力系数的1.5～1.7倍.结合图3可知，这是由于离心力的作用使得外壁壁面处的轴向速度梯度远远大于内加热壁面，造成外壁面的剪切力远大于内壁面所引起的.

图5还表明各边界面上Re=20 000时的fRelocal均明显大于Re=12 000时的fRelocal，说明Re的增大会使各边界面的fRelocal值明显增大.但图6给出的κ对fRelocal的影响却与Re对fRelocal的影响不尽相同：随着κ的增大，外壁面和内壁面上近二次涡中心位置处的fRelocal均会增大，但内壁面中心区域的fRelocal却随κ的增加而变小.平均阻力系数fRem随着Re或κ的增加而增大，fRem与Re和κ的关系如图7所示.

表1给出了无量纲挠率对三角形螺旋流道内充分发展段湍流流体流动阻力的影响.由表1可知：当κ=0.1时，挠率τ对流体阻力的影响较小，且随着挠率τ的增大，fRe先减小后增大，这与文献[13]中给出的挠率对矩形螺旋流道内流体阻力影响的结论相似.

图5　不同Re时内、外壁面的局部阻力系数

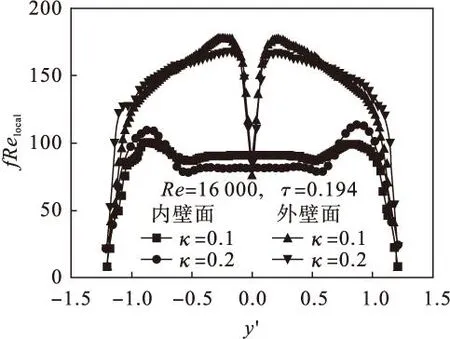
图6　κ不同时内壁面和外壁面上

图7　κ和Re 对fRem的影响

RefReτ=0.006τ=0.01τ=0.021000076.6876.4877.731200087.8487.6189.081400098.6298.36100.0616000109.07108.78110.6920000129.19128.85131.20

3结论

采用CFD软件对等腰直角三角形螺旋流道内湍流流体的流动进行了数值模拟，得到充分发展条件下流体的速度场和湍动能分布，分析了Re、无量纲曲率及挠率对充分发展段流体流动阻力的影响.

(1) 等腰直角三角形螺旋流道内湍流流体的二次流为稳定的两涡结构，湍动能的最大值集中在靠近壁面附近的区域，且外壁侧的湍动能要明显大于内壁侧.随着Re的增大，二次流强度和湍动能均增强.

(2) 同一Re时，上、下两45°角顶点处边界fRelocal接近于0，内壁面的局部阻力系数关于y′=0点基本对称，其fRelocal的峰值出现在靠近上、下二次涡的壁面处.外壁面fRelocal随y′变化的曲线形状与内加热壁面的大不相同.外侧壁面具有最大轴向速度梯度处出现其fRelocal的最大值.在所研究的Re范围内，外侧壁面的平均阻力系数约为内侧壁面平均阻力系数的1.5～1.7倍.

(3) 增大Re，会使各边界的fRelocal值明显增大，但增大曲率，内壁面中心区域的fRelocal却随κ的增加而变小，总平均阻力系数fRem随着Re或κ的增大而增大.

(4) 在所研究的范围内，无量纲挠率对流体阻力的影响较小，曲率κ不变时，挠率τ增大，fRe先减小再增大.

参考文献：

[1]Cope R C,Hanks R W.Transitional Flow in Isosceles Triangular Ducts[J].Industrial & Engineering Chemistry Fundamentals,1972,11(1):106-117.

[2]沃林，葛景信，蔡祖恢.三角形通道入口段流动与换热性能的研究[J].上海机械学院学报,1989,11(4):1-12.

[3]Abdel-wahed R M,Attia A E.Fully Developed Laminar Flow and Heat Transfer in an Arbitrarily Shaped Triangular Duct[J].Wärme-und Stoffübertragung,1984,18(2):83-88.

[4]祝世兴，王致清.等腰三角形管道进口段流动阻力研究[J].应用数学和力学,1993,14(9):793-807.

[5]祝世兴，高德，王致清.任意三角形管道层流进口段流动阻力研究[J].水动力学研究与进展,1993,8(增刊):508-517.

[6]Ray S,Misra D.Laminar Fully Developed Flow Through Square and Equilateral Triangular Ducts with Rounded Corners Subjected to H1 and H2 Boundary Conditions[J].International Journal of Thermal Sciences,2010,49(9):1763-1775.

[7]Collins W M,Dennis S C R.Steady Flow in a Curved Tube of Triangular Cross Section[J].Proceedings of the Royal Society of London Series A,Mathematical and Physical Sciences,1976,352(1669):189-211.

[8]Collins W M,Dennis S C R.Viscous Eddies Near a 90° and a 45° Corner in Flow Through a Curved Tube of Triangular Cross-section[J].Journal of Fluid Mechanics,1976,76(3):417-432.

[9]Nandakumar K,Mees P A J,Masliyah J H.Multiple,Two-dimensional Solutions to the Dean Problem in Curved Triangular Ducts[J].Physics of Fluids A:Fluid Dynamics,1993,5(5):1182-1187.

[10]王翠华,唐密,吴剑华,等.等腰直角三角形截面螺旋流道内层流流体的流动特性[J].过程工程学报,2012,12(5):754-759.

[11]王翠华，刘胜举，吴剑华.三角形螺旋流道层流流动及换热特性模拟[J].化学工程,2013,41(6):30-34.

[12]Kumar V,Gupta P,Nigam K D P.Fluid Flow and Heat Transfer in Curved Tubes with Temperature-dependent Properties[J].Industrial & Engineering Chemistry Research,2007,46(10):3226-3236.

[13]张丽.螺旋片强化的套管换热器壳侧流体流动及复合强化传热[D].天津:天津大学出版社,2011:41-45.

Simulation on Turbulent Flow Characteristics in Helical Ducts with Right-angled Isosceles Triangle Cross Section

LIU Sheng-ju,WANG Cui-hua,WU Jian-hua,WANG Run-kang

(Shenyang University of Chemical Technology, Shenyang 110142, China)

Abstract:With CFD software,the turbulent flow characteristics in helical ducts with right-angled isosceles triangle cross section were simulated.The velocity fields of fully developed turbulent flow of numerical models with different structure parameters were calculated.The distribution of the local coefficient of resistance(fRe(local)) on outer walls and inner wall was obtained and the effect of curvature ratio,torsion and Reynolds number on the characteristics of the flow resistance was analyzed.The results indicate that the secondary flow structure at turbulent flow in the helical ducts is with two steady vortexes.The velocity gradient near the outer walls is more larger than that near the inner wall due to the effect of centrifugal force，and the mean flow resistance coefficient(fRem) of the outer walls is about 1.5～1.7 times that of the inner wall in the simulate range.The mean flow resistance coefficient on the walls increase with greater value of dimensionless curvature ratio and Reynolds number,whereas the dimensionless torsion has weaker effect on fRem.

Key words:helical duct;triangle cross section;secondary flow;turbulent flow

中图分类号：TQ021.1

文献标识码：A

doi:10.3969/j.issn.2095-2198.2016.01.013

文章编号：2095-2198(2016)01-0065-05

作者简介：刘胜举(1989-)，男，河南郑州人，硕士研究生在读，国家奖学金获得者，主要从事流体机械及工程方面的研究.通讯联系人：王翠华(1978-)，女，山东济宁人，博士，讲师，主要从事化工过程流体流动及换热强化的研究.

基金项目：中央支持地方高校发展专项资金项目(辽财指教[2010]865号)

收稿日期：2013-12-20