Left-Right Non-Linear Dynamical Higgs∗
2016-05-09JingShuandJuanYepes
Jing Shu and Juan Yepes
State Key Laboratory of Theoretical Physics and Kavli Institute for Theoretical Physics China,Institute of Theoretical Physics,Chinese Academy of Sciences,Beijing 100190,China
1 Introduction
The LHC has experimentally confirmed the existence of a new scalar resonance[1−2]in our nature,that resembles the long ago proposed Higgs boson.[3−5]Such discovery establishes thus the Standard Model(SM)as a successful and consistent framework of electroweak symmetry breaking(EWSB),with the Higgs particle signalling different BSM scenarios.In one class of models,the Higgs is just an elementary scalar doublet linearly transforming under the SM gauge group SU(2)L×U(1)Y.Alternatively,the Higgs particle could emerge from a given strong dynamics at the TeV or slightly higher scale,and arising either as an EW doublet or as a member of other representations.In any case,a new physics(NP)at the TeV scale is demanded and lighter exotic resonances will in general play a role at such scale,as it is commonly proposed in many theoretical models.
In this work an EW strongly interacting sector coupled to the light Higgs particle will be assumed.Furthermore,motivated by the high energy regimes reachable at the LHC and future colliders,this work faces the hypothetical situation of non-zero signals arising out from some emerging new physics field content in the nature,more specifically,from spin–1 resonances driven by extending the SM local gauge symmetry GSM=SU(2)L×U(1)Yto the larger local group G=SU(2)L×SU(2)R×U(1)B−L(see[6–7]for left-right symmetric models literature).The underlying framework employs a non-linear σ-model for the strong dynamics giving rise to the Goldstone bosons(GB),i.e.the W±Land ZLlongitudinal components that lead to introduce the Goldstone scale fL,together with the corresponding GB from the extended local group,the additional W±Rand ZRlongitudinal degrees of freedom and the associated Goldstone scale fR.Their transformation are customarily parametrized via the dimensionless unitary matrix U(x),more specifically through UL(x)and UR(x)for the symmetry group SU(2)L×SU(2)R,and defined as the exponential of the GB fieldsvia
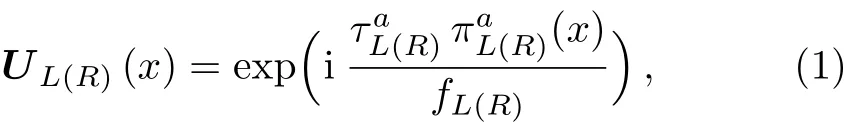

The whole tower of linearly independent left,right and the interplaying left–right handed operators(LH,RH and LRH respectively)for the CP-conserving bosonic sector has been established1through[10]and it is summarized again for the purposes of our left-right model analysed here. Such scenario may be considered as a generic UV completion of the low energy non-linear treatment of Refs.[11–15]and[9,16].Its physical impact has been studied by integrating out the right handed gauge sector from the physical spectrum,leading the RH and the mixing LRH operators to collapse directly onto the LH sector,and inducing therefore corrections weighted by powers of the parameterϵ≡ϵcC,LR,with the scale ratio ϵ≡fL/fRand the coefficient cC,LRencoding the strength of the mixing among the LH and RH gauge masses.This feature leads to modify,consequently,the electroweak precision data(EWPD)parameters,the triple gauge couplings(TGC),hV V-couplings and the anomalous quartic gauge couplings(QGC).Corresponding allowed ranges for the involved coefficients will be also reported.
The recently observed diboson excess at the ATLAS and CMS Collaborations around the invariant mass of 1.8 TeV–2 TeV will entail a scale fR∼ (6–8)TeV,leading to a negligible parameter∼ 10−4and suppressing therefore all the linear and higher ¯ϵ-effects induced by the RH and LRH operators.These effects could be enhanced either via larger strength of the coefficient cC,LR,or via NP effects from the right handed gauge sector around the EW scale fLtogether with a strength contribution of cC,LRaround its maximal bound.It will be seen that the former scenario spoils the EW gauge masses,whereas the latter one points towards∼ 10−2.The set of relevant non-linear LH,RH,and LRH operators will be completely identified for the latterand by disregarding:(i)irrelevant LH operators with negligible physical impact on the observables considered for the hV V-bounds;(ii)irrelevant operators for the non-linear realization of the dynamics and redundant for the massless fermion case;(iii)operators without any direct contribution to the pure gauge and gauge-Higgs couplings.It will be shown also that the diboson excess suggests to parametrize low energy effects via a much smaller effective operator basis as theϵ-suppression entails.
This work is split into:Sec.2 describes the EW effective Lagrangian following the light dynamical Higgs picture in Refs.[9–10,16,20–21],(see also Refs.[22–24]and for a short summary on the subject[25]),focused only in the CP-conserving bosonic operators,2See Refs.[21–22,26–27]for non-linear analysis including fermions.and providing all the LH,RH and LRH operators of the model up to p4-order in the effective expansion.The mixing effects for the gauge masses triggered by the LRH operators and the corresponding gauge physical masses are analysed in Subsec.2.1.The effects by integrating out the RH fields are studied in Subsec.2.2.Section 3 describes the phenomenology implied by the model and the allowed ranges for the involved coefficients weighting the effective operators.Section 4 comments on the recently observed diboson excess and its implications for the operator basis of our model,in particular on the relevant LH,RH and LRH operators for each one of the situations dictated byFinally,Sec.5 summarizes the main results.
2 E ff ective Lagrangian
The underlying strong dynamics assumed for this framework entails effective NP departures with respect to the SM Lagrangian L0and will be encoded through Lchiralas

Focusing only on the bosonic interacting sector,the first three pieces in Lchiralare

where the adjoints SU(2)L(R)-covariant vectorialtogether with the covariant scalar TL(R)objects,are deif ned as

with the corresponding covariant derivative for both of the Goldstone matrices UL(R)(x)introduced as

with the SU(2)L,SU(2)R,and U(1)B−Lgauge fields denoted byand Bµcorrespondingly,and the associated gauge couplings gL,gRand g′respectively.The usual SM strength gauge kinetic terms canonically normalized,the h-kinetic terms and the effective scalar potential V(h)are present at L0in(4).Theand ZLmasses(before considering the corresponding RH and mixed LRH handed terms introduced a posteriori)and their couplings to the Higgs field h can be read from the last term in the second line of L0.The custodial breaking p2-operator turns out to be strongly bounded phenomenologically,being thus left for the NP departures analysed later.[16]The scale factor of Tr()entails GB-kinetic terms canonically normalized,in agreement with the UL-definition in(1).The corresponding SU(2)R-counterparts for the strength gauge kinetic term and the custodial conserving operator are parametrized by L0,Rin(5),implying thus an additional scale fRthat encodes the new high energy scale effects introduced in the scenario once the SM local symmetry group GSMis extended to G.
Operators mixing the LH and RH-covariant are also constructable in this approach via the proper insertions of the Goldstone matrices ULand UR,more specifically,through the following definitions[10]


where the suffix L(R)labels all those operators set constructed out by means of the SU(2)L(R)building blocks in(8).The contribution∆LCP,Lhas already been provided in Refs.[9,16]in the context of purely EW chiral effective theories coupled to a light Higgs,whereas part of∆LCP,Land∆LCP,Rwere partially analysed for the leftright symmetric frameworks in Refs.[17–18],and finally completed in the recent work[10](for the corresponding CP-violating part see Ref.[19]).Both of the contributions∆LCP,Land∆LCP,Rcan be further written down as

where cB,cGand ci,χare model-dependent constant coefficients,whilst the first three terms of∆LCP,Lin(10)and the first term in(11)can be jointly written as


with suffix χ labelling again as χ =L,R,and the generic Fi(h)-function of the scalar singlet h is defined for all the operators following definition(2).Finally,the last two terms in the second line of∆LCP,Lin(10)account for all the possible pure Higgs interactions,with the p2and p4-operators PHand P?Hrespectively as
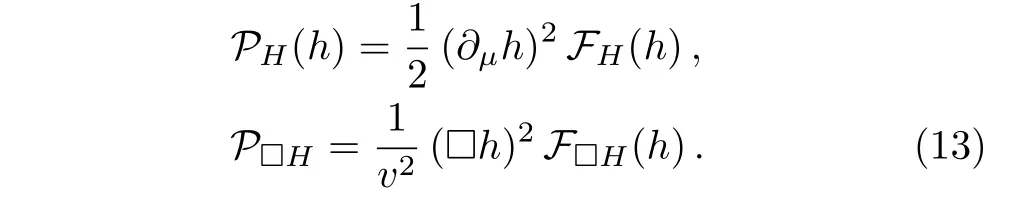
The set of 26 CP-conserving pure gauge and gauge-h non-linear operators encoded by Pi,L(h)(fourth term in∆LCP,L,Eq.(10))have completely been listed in Refs.[9,16].On the other hand,the symmetric counterpart made out of the 26 CP-conserving operators Pi,R(h)(second term in∆LCP,R,Eq.(11))were recently reported in Ref.[10].In total there are 52 non-linear operators,38 of them(19 Pi,L+19 Pi,R)had already been listed in Refs.[17–18],whilst 14 additional operators were found(7 Pi,L+7 Pi,R)in[10]with respect to[17–18](seven of them,corresponding to χ=L,were already reported in[9,16]).See[10]for the complete list of operators∆LCP,Land related discussion.
Finally,∆LCP,LRparametrizes any possible mixing interacting term between the SU(2)Land SU(2)R-covariant objects up to the p4-order in the Lagrangian expansion,permitted by the underlying left-right symmetry,and encoded through[10]

where the index j spans over all the possible operators that can be built up from the set of 26 non-linear operators Pi,χin(10)–(11)(fourth and second terms respectively),and here labelled as Pi(j),LR(as well as their corresponding coefficients ci(j),LR).The first term in∆LCP,LRencodes the non-linear mixing operators

corresponding to the “mixed” versions of{PW,χ,PC,χ,PT,χ}in(12),with PW,LRmissing in Refs.[17–18].The complete set of operators Pi(j),LRin the second term of∆LCP,LRhave been fully and recently listed in Refs.[10].Both of the previously described CP-conserving contributions∆LCPand∆LCP,LRhave been completely listed and studied in[10],whereas their corresponding CP-violating counterparts analysed in Ref.[19].Notice that in the unitary gauge,non-zero mass mixing terms among the LH and RH gauge fields are triggered by the operator PC,LR,leading to diagonalize the gauge sector in order to obtain the required physical gauge masses.
Non-linear approaches have already been linked to the linear effective scenarios explicitly implementing the SM Higgs doublet through,[9,16]where all the operators in(10)were respectively weighted by powers of ξ≡ v2/f2L,in order to keep track of their corresponding operator siblings in the linear regime.In fact,operators in(4),and those in the first line of(10),as well as P1−5,L,had been already pointed out in the analysis of the linear-non linear connection of the SILH framework.[28−29]Indeed,for the ξ-small limit,all the operators weighted by ξn>2are negligible and the resulting Lagrangian is directly linked to the SILH treatment.Similar analysis has been recently done for the Higgs portal to scalar dark matter in the context of non-linearly realised electroweak symmetry breaking.[30]For the assumed non-linear scenario in this work,such linking between both of the EFT sides implies the corresponding left-right symmetric extension of the effective linear approaches and it is beyond the scope of this work.
An interesting feature of this scenario arises once the gauge field content WRis integrated out from the physical spectrum at low energies.In fact,the RH terms encoded through the Lagrangian L0,Rin(5),will impact directly onto the left handed ones of L0in(4).Similarly,the RH and LRH terms parametrized by∆LCP,Rand∆LCP,LRin Eqs.(11)and(14)will a ff ect those ones from∆LCP,Lin(10).These modifications will alter therefore the effective couplings sourced by the whole Lagrangian L0+∆LCP,L,specifically,the triple and quartic gauge boson couplings,as well as the gauge bosons-Higgs couplings.Non-zero contributions on the EWPD parameters S and T will also be induced as it will be seen later.At higher energies,when the right handed gauge fieldsare still playing a role,mixing effects among them and the left handed gauge field sector will be triggered by the PC,LRin(15).Those effects are treated in the following section.
2.1 Rotating to the Physical Sector
At the unitary gauge,the non-linear chiral effective Lagrangian Lchiralin(3)sources the following mass terms for both of the charged and neutral gauge sectors
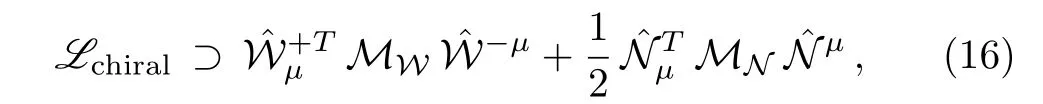
with the gauge basis defined by

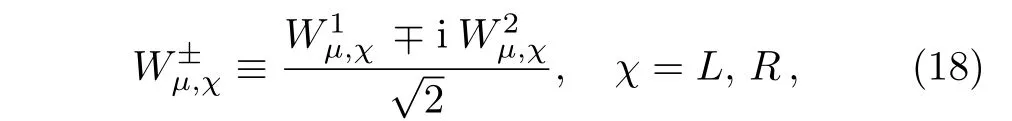
and the mass matrix for the charged sector written as

with the parameter λ defined as

The corresponding mass matrix for the neutral sector reads as

where it has been introduced the definitions
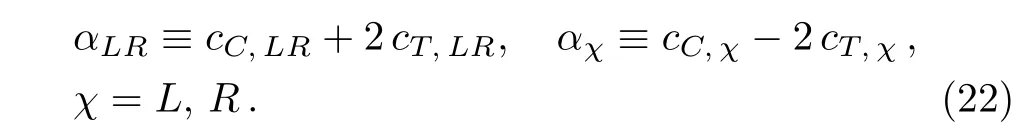
The latter matrices can be diagonalized via the following field transformations
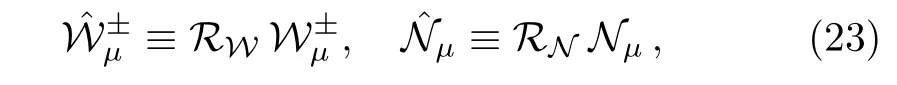
with the mass eigenstate basis defined by

The rotation matrix for the charged sector in Eq.(23)is given by

with the mixing angle ζ for the charged sector directly depending on the parameter λ and the mixing coefficient cC,LR.Expanding up to the order O(λ2)in the limit fL≪fR,the charged gauge masses are

For the the neutral sector we have the real symmetric 3×3 matrix in Eq.(21),then an orthogonal rotation via the Euler-type angles parametrization is in order to diagonalize it.Such angles turn out to be the Weinberg mixing angle θWand the analogous mixing angle θRfor the SU(2)R×U(1)B−Lsector defined correspondingly as

where it has been employed in(28)the link among the SU(2)L,U(1)B−Land the SM hypercharge gauge couplings as

The third angle ϕ can be linked to the latter two through

The rotation matrix for the neutral sector becomes parametrized then as

Expanding up to the order O(λ2)(in the limit fL≪ fR)the neutral gauge masses are

with tanθR≡ tR.The well measured MZ-mass strongly constrains the coefficient αLin(32),and therefore the contribution from the operators PC,L(h)and PT,L(h).Likewise,the MW-mass bounds tightly constrains the contribution from PC,R(h)in(26).A mass prediction for the extra neutral gauge field Z′can be inferred from(32)in terms of the W′-mass and the RH gauge coupling gRvia the mixing angle θRin(28).In fact,interpreting the observed excess at the ATLAS and CMS Collaborations around invariant mass of 1.8 TeV–2 TeV to be induced by a W′-contribution,and assuming the coupling gRin the range gR≈ 0.45–0.6 as determined in Ref.[31]by comparing the W′production cross section to the CMS dijet excess,[32]it is possible to predict the mass range 2.4 TeV A higher energy scale fRpoints in general towards higher masses MW′and MZ′,additionally entailing a vanishing mixing angle ζ among the charged gauge fieldsandas λ → 0(see Eqs.(17),(24),and(25)),neither a mixing among the set of neutral fieldswith the field(see Eqs.(17),(24),and(31))and therefore right handed gauge fields directly linked to the eigenstate basis asandHeavy right handed gauge fields can thus be integrated out from the physical spectrum of the model,triggering therefore physical effects that will be manifested at lower energies in the effective Lagrangian.Such procedure together with the induced effects it leads to,will be analysed via equations of motion for the right handed fields in the following section. From the equations of motion for the gauge and Higgs fields(Eqs.(75)–(77),Appendix B)it is possible to integrate out the RH gauge fields from the physical spectrum.In fact,at low energies one obtains from the EOM that can be translated into the unitary gauge as After such field redefinition,all the couplings and operator coefficients will be shifted,a ff ecting thus the final form for the TGV couplings,anomalous quartic gauge and gauge-Higgs couplings,and modifying as well the final expressions for the EWPD parameters as it will be seen in the next sections.The final Lagrangian at low energies,here denoted bywith respect to Lchiralin(3),will be given by where the first component reads as and the scale f is given by the redefinition Table 1 The initial coefficient ci,Lfrom the LH operator Pi,L(1st column)receives a contribution from the RH Pi,R(2nd column),plus a combination from the mixing LRH Pi(j),LR(3rd column),and for each one of the Pi,L(4th column).The sum of the values at the first,second and third column defines the redefined coefficientsafter integrating outfrom the physical spectrum.The parameter¯ϵ stands for¯ϵ≡ϵcC,LRwith ϵ≡fL/fR. Table 1 The initial coefficient ci,Lfrom the LH operator Pi,L(1st column)receives a contribution from the RH Pi,R(2nd column),plus a combination from the mixing LRH Pi(j),LR(3rd column),and for each one of the Pi,L(4th column).The sum of the values at the first,second and third column defines the redefined coefficientsafter integrating outfrom the physical spectrum.The parameter¯ϵ stands for¯ϵ≡ϵcC,LRwith ϵ≡fL/fR. Pi,L Pi,R Pi(j),LR i cW,R−4c1,R−4c12,R+¯ϵ2(cW,R−4c12,R)–B+¯ϵ(2cW,R − 4c1,R − 8c12,R)ci,L ¯ϵ2ci,R ci−¯ϵci,LRW ci,L ci,R {−2cC,LR,−2cT,LR} {C,T}ci,L 2(−2ci,R+cW,R − 4c12,R)+ ¯ϵ2¯ϵ 2(cW,R−4c12,R) ¯ϵ 4(4c12(1)−cW,LR)+1 4(4c12(1)−cW,LR) 1¯ϵ2 2(2ci,R+c3,R+2c13,R)+¯ϵ3 2(c3,R+2c13,R) 1 ci,L 2(2c13(2)+c3(2))−¯ϵ2 2(2c13(4)+c3(4))2 2(2(−c13(2)+c13(4)+c2(1))−c3(2)+c3(4))ci,L−¯ϵ3ci,R¯ϵ2(ci(1)+ci(4))−¯ϵ(ci(2)+ci(3))3,13 ci,L−¯ϵ−¯ϵ c17(2) 4 ci,L ¯ϵ2ai,R ai,L(ai,Rci,R+a17,Rc17,R) − ¯ϵ2a17,R ai,L c17,R ¯ϵa17(2)ai,L c17(2)+a17(2)ai,L ci(2) 5,10,17,19 ci,L¯ϵ4ci,R¯ϵ2(ci(1)+ci(2))−¯ϵci(3)−¯ϵ3ci(4)6,26 ci,L ¯ϵ2ai,R ai,L ci,R −¯ϵai(1)ai,L ci(1) − ¯ϵai(2)ai,L ci(1) 7,25 ci,L ¯ϵ2a2 i,R ai,L ci,R−¯ϵai(1)ai,L i(1)a2i,L ci,R−¯ϵa2 a2i,L ci(1) 8,20,21,22 ci,L ¯ϵ2ci,R −¯ϵci(1) 9,12,15 ci,L¯ϵ4ci,R¯ϵ2(ci(1)+ci(2)+ci(5))−¯ϵci(3)−¯ϵ3ci(4)11 ci,L−¯ϵ3ci,R−¯ϵ(ci(1)+ci(3)+ci(5))+¯ϵ2(ci(2)+ci(4)+ci(6))14 ci,L−¯ϵ3ci,R−¯ϵ(ci(1)+ci(4)+ci(6))+¯ϵ2(ci(2)+ci(3)+ci(5))16 ci,L−¯ϵ3ai,R ai,L ci,R ci,L ¯ϵ4ci,R−¯ϵ 18+ ¯ϵ2 ai,L(ci(1)ai(1)+ci(3)ai(3)+ci(6)ai(6))ai,L(ci(2)ai(2)+ci(4)ai(4)+ci(5)ai(5))−¯ϵ(ci(3)+ci(6))−¯ϵ3(ci(4)+ci(5))23+¯ϵ2(ci(1)+ci(2)+ci(7))ci,L ¯ϵ4ci,R−¯ϵ(ci(3)+ci(6))−¯ϵ3(ci(4)+ci(5))24+¯ϵ2(ci(1)+ci(2)+ci(7)+ci(8)) TheEW gaugemassMWstronglyconstrainsthe quadratic contribution of the LRH operator PC,LR(h)in(38)as Notice that a mixing term in the kinetic gauge sector is induced at low energies,driving thus additional effects when diagonalizing such sector,as well as a nonzero contribution to the S-parameter as it will be seen as a posteriori.The second component in(35)is basically the Lagrangian in(10)but the gluonic operator PG(h),and with the coefficients{cB,ci,χ}properly redefined as{cB,ci,χ}→{}in order to account for the induced effects after removing away the RH gauge fields from the physical spectrum.Table 1 displays all the initial contribution ci,Lfrom the LH operators Pi,L(1st column)receiving a contribution from the RH Pi,R(2nd column),plus a combination from the mixing LRH Pi(j)(3rd column),and for each one of the LH non-linear operators Pi,L(indicated at the 4th column).The sum of the values at the first,second and third columns determines the coefficients.It is possible to infer that for the limiting hierarchical case fL≪fRat low energies,the set of non-linear operators is sensitive to the contributions from both of the RH operators and the mixing LRH set This will be of relevance for the EWPT parameters S and T,as they are sensitive to the effects from P1,Land PT,Lrespectively,being thus a testers of the emerging NP effects after removing the RH gauge field content. Furthermore,the triple gauge–boson couplings γ W+W−and W+W−Z(TGC)will be also sensitive to the induced effects. In particular,the vertexes,with V≡{γ,Z},will receive nonzero contributions from both of{P1,L,P2,L}as it will be shown later. Likewise,pair gauge bosons-Higgs couplings will be a ff ected too. In fact,the vertexes{FµνFµνh,ZµνZµνh,FµνZµνh,ZµZµν∂νh,ZµFµν∂νh},and{}will depend of linear combinations of the operators in(40).Additional contributions from the mixing LRH operator PC,LRare also found for the interacting terms{},as it will be described in the next sections. The contributions to the LH operators in Table 1 are weighted by powers of the parameter¯ϵ introduced in(33).Two quantities control thus the low energy effects induced by the RH and LRH operators:(i)the mixing coefficient cC,LRthrough the custodial mixing operator PC,LR(h);(ii)and the scale ratio ϵ≡ fL/fR.In general fL≪ fR,therefore the small range of cC,LRadditionally suppresses the ϵ-effect.Nonetheless,sizeable linear ¯ϵ-effects will arise contributing to the LH operators for a cC,LRaround its maximal bound together with NP effects not far above the scale fLas it will be analysed later. To analyse the physical impact and the low energy effects sourced by removing the heavy right handed gauge fields,it is necessary to establish the observables that will be set as the parameters input of the model.The renormalization procedure accounting for this is described in the following section. Before integrating out the gauge fieldsand with fermion masses neglected from the beginning,the SM-like Lagrangianin(35)(SM-like for the case of αB=αWB= αW=0)contains five electroweak parameters{gs,g,g′,v,λ},with the last one as the h self-coupling.The following set of well-measured observables serve to constrain such set of EW parameters and defines the socalled Z-scheme • Strong coupling constant αs,world average,[34] •Fermi constant GF,extracted from the muon decay rate,[34] • Fine structure constant αem,extracted from Thomson scattering,[34] •Gauge boson mass mZ,extracted from the Z lineshape at LEP I,[34] • Higg mass mhnow measured at LHC.[35−36] Expressions depending on the parameters g,g′,v(and e)or the weak mixing angle θWwill be arranged as combinations of the experimental inputs above.In fact,the electric charge e,the weak mixing angle θW,and the vev scale v can be defined as and therefore the couplings g and g′as Workingin theunitarygaugetoanalysetheimpactthatthecouplingsof∆¯LCPin(35)have on L0,it is straightforward to show that the set{PB,PW,L,PG,PH,P1,L,P12,L}introduce corrections to the SM kinetic terms,and in consequence field redefinitions are necessary to obtain canonical kinetic terms.Among the latter operators,{PB,PW,L,PG}can be considered innocuous operators with respect to L0,as the impact on the latter of cB,cW,L,and cGcan be totally eliminated from the Lagrangian via field and coupling constant redefinitions that will impact on certain BSM couplings in∆L involving external scalar fields.Implementing canonical kinetic terms,it is then easy to identify the contribution ofto the input parameters:3Following the convention in Refs.[9,16],BSM corrections for the input parameters will be generically denoted by “δ”,whereas the predicted measurable departures from SM expectations will be indicated by “∆”. where the Fermi constant and the Higgs mass are not corrected by the operators contribution at tree level,and linear terms in the coefficients αWBandhave been kept.All other SM parameter incan be expressed in terms of the input parameters described above as described in the next. W mass Including the effects from the operators in∆in(35),the predicted mass departures with respected to the mass value in(26)as if cients cW,sW,c2W,and s2Wwill stand for cW≡ cosθW,sW≡ sinθW,c2W≡ cos(2θW),and s2W≡ sin(2θW)respectively.Notice two different terms contributing in Hereafter the compact notation encoded through the coef-(46):one accounting for the effects of integrating out the RH fields via αWBin(37),and one more accounting for the combined effects from the non-linear operators themselves plus the integration-out of the RH fields,via the redefined operator coefficients{}.From Table 1,the coefficientreceives direct contributions from the set{cT,L,cT,R,cT,LR},whereas for the hierarchical case fL≪fR(with g′≪gR)receives relevant contributions from the LH operator P1,Lplus a combination from the LRH set{PW,LR,P12(1)}.The coefficient ˜c12,Lonly gains contributions from P12,L.So,all in all the W-mass prediction turns out to be sensitive to the operators set At the hierarchical limiting case the mass variation in(46)becomes where{cT,LR,cW,LR}are correspondingly the operator coefficient of{PT,LR,PW,LR}in(15),whilst c12(1)is the corresponding one in(14)for P12(1),LR(see Appendix A2). S and T Parameters Integrating out the right handed gauge fields together with the non-linear operators lead to the tree-level contributions to the oblique parameters S and T,[37]as Notice from(49)that only the S-parameter is sensitive to the effects of the RH fields integration via αWB.Furthermore,combined effects from the non-linear operators plus the removal ofcontribute to S via the redefined coefficient.For the hierarchical case fL≪fR(with g′≪gR),receives relevant contributions only from the set{P1,L,PW,LR,P12(1),LR}.In this case the S-parameter reduces to The set of custodial breaking operators{PT,L,PT,R,PT,LR}contribute to T via the coefficient.From Table 1 the T-parameter turns to be then The experimental values S =0.00±0.10 and T =0.02±0.11[34]allow to infer the rough order of magnitude estimates {c1,L,cW,LR,c12(1)} ∼ 10−3and{cT,L,cT,R,cT,LR} ∼ 10−3respectively. More precise ranges for all these coefficients can be derived from a global fit to the EWPD parameters as it will be seen in the next sections. The final effective operators contained inweighted by the redefined operators coefficients{},give rise to triple gauge-boson couplings γ W+W−and W+W−Z(TGC).These couplings can be generically described through the customary parametrization[38] where V ≡ {γ,Z}and gWWγ≡ e,gWWZ≡ ecW/sW,withand Vµνstanding for the kinetic part of the implied gauge field strengths.Electromagnetic gauge invariance requires=1 and=0,in consequence the CP-even TGC encoded in(52)depends in all generality on six dimensionless couplings,and κγ,Z.Their SM values are=κγ=κZ=1 and=0.Couplings λγ,Zturn out to be vanishing up to the p4For a general discussion on possible “o ff-shell” vertices associated to d=4 and d=6 operators see Ref.[39].-order for the non-linear treatment assumed in here.As long as CP-even bosonic p6-operators are considered,a nonvanishing contribution for such couplings is turned on.Additionally,the couplingshave been introduced to account for the contributions associated to the operators containing the contraction,with its correspondingvanishing only for on-shell gauge bosons.When fermion masses are neglected,such contraction can be disregarded4in the present context(see Appendix B). Table 2 TGV couplings from the Lagrangian LTGVin(52)following standard convention in Ref.[38].The total TGV coupling(1st column)is made out of:the usual SM contribution(2nd column)+additional effects after integrating out the fields (3rd column)+the combined terms yielded by the RH fields removal and the non-linear operators all together(4th column). Table 2 TGV couplings from the Lagrangian LTGVin(52)following standard convention in Ref.[38].The total TGV coupling(1st column)is made out of:the usual SM contribution(2nd column)+additional effects after integrating out the fields (3rd column)+the combined terms yielded by the RH fields removal and the non-linear operators all together(4th column). TGC SM Integrating Integrating+Operators 1 − 2s4(())gZ1 W 1−4e2˜c3,L αWB ˜cT,L−4e2˜c12,L−s2W˜c1,L c2Ws2W 2c2W κγ 1 cW c2W s22W(2˜c1,L+2˜c2,L+˜c3,L+4˜c12,L+2˜c13,L)κZ 1 −s2W sW αWB −e2(−(1/c2W+3)˜c12,L+˜c3,L+2˜c13,L s2W)2c2W αWB e2 s2W+2˜c1,L c2W+2˜c2,L c2W+˜cT,L 2c2W gZ5−−−4e2 s22W ˜c14,L gγ 6−−e2(4˜c16,L s2W ˜c9,L)gZ6−−e2 s22W−˜c9,L c2W Table 3 QGC values from LQGVin(53).All the couplings are split as in Table 2. The set of TGC parametrized through LTGVin(52)are listed in Table 2(1st column),being split all of them into their corresponding SM contribution(2nd column),the additional effect after integrating out the gauge fields(3rd column),plus the combined terms accounting for the combined effect by removing the RH fields and the non-linear operators via redefined coefficients(4th column).From Tables 1–2 and the operators set in(40)–(42),it is inferred that •No effects are induced onto the TGC set{}after integrating out the RH fields,only the combined effects from the removal plus the non-linear operators through the redefined coefficients.No RH operators neither LRH mixing ones contribute to them. The quartic gauge-boson couplings(QGC)can be parametrized in the following Lagrangian where again V ≡ {γ,Z}.All these couplings are gathered up in Table 3,where a similar splitting for each one of them is done alike to the previous TGC case.Likewise it is inferred: Table 4Triple gauge-Higgs couplings from LhV Vin(54).The notationstands for,withthe redefined operator coefficients and aifrom the F(h)-definition in(2). Table 4Triple gauge-Higgs couplings from LhV Vin(54).The notationstands for,withthe redefined operator coefficients and aifrom the F(h)-definition in(2). hV V SM Integrating Integrating+Operators g(1)γγh − − −1)2e2(˜aW,L−4(˜a1,L+˜a12,L)+˜aB)g(1)hZZ − − −1(c2W(˜aW,L − 4˜a12,L)2e2+4˜a1,L+˜aBs2W(cW(4˜a12,L−˜aW,L)s2W c2W )g(1)γhZ − − e2+4c2W˜a1,L +˜aBsW s2W sW cW g(1)hWW − − −e2 ˜aW,L)(2˜a4,L g(2)hZZ − − e2 s2W s2W c2W−˜a5,L+2˜a17,L g(2)(2˜a4,L+˜a5,L+2˜a17,L)g(2)γhZ − − −2e2 hWW − − −e2 s2W s2W ˜a5,L g(3)hZZ − − −4e2 s22W(˜a10,L+2˜a19,L)g(4)hZZ − − −4e2 hWW − − −e2 s22W(˜a9,L+2˜a15,L)g(3)s2W ˜a10,L g(4)hWW − − −2e2 ˜a9,L((˜aC,L−˜cC,L)−4e2cWs2W˜c12,L s2W )g(5)hWW 2c2W −2c2Ws2WαWB c2W+8e2˜c1,L+2˜cT,L−cH g(6)hWW − − −2e2 s3W s2W ˜a7,L ))g(5)hZZ 1 s2WαWB 1((c2W˜c12,L 2−2¯cC,LR+˜aC,L−2˜aT,L+8e2 s2W−˜c1,L −cH g(6)hZZ − − −4e2 s22W(˜a7,L+2˜a25,L) Table 4 collects all the couplings. All them have no contributions after integrating out the RH fields,butwhereasthesetis sensitive to the operatorsandPW,LR,P12(1)}for the hierarchical case,according to the involved coefficient dependence in Table 1. (i)S and T parameters bounds The parameters S,T,U are precisely obtained through a global fit to electroweak precision data,resulting in the current values and correlation matrix[34] Table 5 Bounds at 95%CL for each one of the operator coefficients in(50)–(51)obtained from(57)(via Table 1).The bound for αWBand for each one of the coefficients involved in the de finition of˜c1,L,i.e.{c1,L,cW,LR,c12(1)},are obtained by setting to zero the rest of them in(57)(1st inequality).The same comment applies for{cT,L,cT,R,cT,LR}(2nd inequality). Through the redefined coefficients in Table 1,allowed ranges for each one of the involved coefficients in(50)–(51)are obtained from(57)and are shown in Table 5. The constrains in Table 5 signal small contributions of the operators{P1,L,PW,LR,P12(1),LR}and{PT,L,PT,R,PT,LR}to the gauge-boson self-couplings and to the present Higgs data.Consequently they will not be included in the following discussion. (ii)TGC BoundsBounds for the TGC can be determined from the two–dimensional analysis in Ref.[40],which was performed in terms of the induced variations of the couplings κγ,and κZ.Such variations are corresponding in this scenario to the sum of the values at the 3rd and 4th columns in Table 2,here denoted as∆κγ,and ∆κZrespectively,and satisfying the relations in Appendix C.From the two-dimensional analysis in Ref.[40]it was obtained Tree-level contributions from the sets{P1,L,PW,LR,P12(1),LR}and{PT,L,PT,R,PT,LR}are generated for the S and T parameters correspondingly(see Eqs.(50)–(51)).The 95%CL allowed ranges for their corresponding coefficients were found in Ref.[16],and can be translated in here,according to(49),as with a correlation factor of ρ=0.11.The corresponding 90%CL ranges for the coefficients c2,Land c3,Lfrom the TGC data were also found,traded here by˜c2,Land,and finally translated to the coefficients shown in Table 6(via Table 1).Finally,notice from Table 2 thatis generated by the operator P14,Lonly.The best current bounds on this anomalous TGC come from W+W−pairs studies and W production at LEP II energies.[41−43]Furthermore,the strongest limits onoriginate from its impact on radiative corrections to Z physics.[44−46]In Ref.[16]were reported the available direct and indirect limits onThe 90%CL region from indirect bounds[44−46]turns out to be∈ [−0.08,0.04],and translated into the corresponding bound for P14,Las5These limits were obtained assuming only a non-vanishing while the rest of anomalous TGV were set to their corresponding SM value.[16] No extra terms contribute in the hierarchical limiting case to the coefficient c14,L.However,linear ¯ϵ–effects would arise from NP not far above the EW scale(ϵ∼ 1)and for an LRH mixing strength from PC,LRclose to its maximal bound in(39).These contributions and their constrains will be analysed later. Table 6 Bounds at 90%CL for each one of the operator coefficients{˜c2,L,˜c3,L},being translated into bounds for{c2,L,c3,L}and{c3(2),c13(2)}according to Table 1. (iii)Bounds on hV V Couplings In Ref.[16],the operators set{PG,PB,PW,L,PC,L,PH,P4,L,P5,L}were bounded from the constraints of the Higgs data on hV V-couplings.Notice from Table 4 that all them contribute to some of the listed hV V-couplings.The set{P7,L,P9,L,P10,L}was not included in the parameter fit as they do not entail a physical impact on the observables considered,whereas the operators set{P12,L,P17,L,P19,L,P25,L}does not contribute relevantly for a non-linear realization of the underlying dynamics(see Ref.[16]for further details). The analysis relies in two operator subsets:in the first one,PC,Lis neglected,whilst for the second one its contribution is connected to that of PH.Furthermore,the sensitivity of the results to the sign of the h-fermion couplings,e.g.sYh(UYQQR+h.c.),is also considered by performing the analysis with both values of the discrete parameter sY=±.The detailed discussion on the performed six-parameter fit,and the implied chi–square analysis using the available data on the signal strengthsµ,by accounting for the data from Tevatron D0 and CDF Collaborations,as well as from the LHC,CMS,and ATLAS Collaborations at 7 TeV and 8 TeV for final states γγ,W+W−,ZZ,Zγ,b¯b,and τ¯τ[47−60]is referred to the reader in[16]and[61–62]for details on the Higgs data analysis. The 90% CL allowed ranges for the coefficients{}6The corresponding bound for the gluonic operator coefficient αG,not listed here neither written down in the gauge-higgs Lagrangian of(54),can be read o fffrom Ref.[16].In addition it has been assumed ai ≈ O(1)in the definitioncan be straightforwardly obtained from the corresponding ones in Ref.[16].The latter ranges can be translated(via Table 1)into ranges for the coefficients{cH,cB,cW,L,c4,L,c5,L},{cW,R,c1,R,c12,R}and c17(2),shown in Table 7.The recent SFitter analysis for a non-linear framework in Ref.[63]allows us also to obtain the corresponding 95%CL allowed ranges collected in Table 7.As suggested in[16],the sensitivity to the coefficients{}can improve by a factor O(3-5)with a similar analysis,according to the expected uncertainties accesible in the Higgs signal strengths from ATLAS and CMS at 14 TeV,and for an integrated luminosity of 300 fb−1.[64−65]Consequently,a similar sensitivity improvement is expected for all the coefficients in Table 1,as they are linked to the redefined coefficients through the relations in Table 7.Finally,the 95%CL ranges from the SFitter analysis are a bit constraining with respect to the 90%CL ranges in Table 7. Table 7 90%and 95%CL allowed ranges(2nd and 3rd columns)for the coefficients{cH,cB,cW,L,c4,L,c5,L},{cW,R,c1,R,c12,R}and c17(2)contributing to Higgs data. The 90%CL ranges for cH correspond to the two analysis in Ref.[16]and for both signs of sY,whereas the reported ranges for{cW,L,c4,L,c5,L}are basically the same for both of the operators subset and for both values of sY.The 95%CL ranges correspond to the recent SFitter analysis in Ref.[63]. In summary,the current bounds from the EWPD analysis for the S and T parameters,as well as the TGC and hV V-couplings bounds,have allowed us to constraint at the thousandth level the coefficients in Table 5(few percent level for cW,LR),at the 10%level those in Table 6(percent level for c3,L),and at 10%(percent level for{c1,R,c12,R})the coefficients in Table 7.Finally,through the aforementioned experimental current bounds we have obtained bounds for the coefficients weighting correspondingly some of the RH and LRH non-linear operators,more precisely,those ones contributing to the LH operators after removing the right handed resonances from the physical spectrum and for the hierarchical case fL≪fR.From the Tables 5–7 and the bound in(39),we have constrained the following RH and LRH operators so all in all are the same operators as in(41)–(42),but PC,R.The latter turns out to be tightly constrained(up tocorrections),together with PC,L,by their corresponding contributions to the charged and neutral resonances masses MW′and MZ′respectively in(26)–(32)as (iv)Anomalous Quartic Couplings Among the operators contributing to the quartic gauge couplings in(53)shown in Table 3,some of them were previously bounded either from EWPD constrains,TGC bounds,or limits on hV V couplings. The remaining five operators giving rise to the purely QGC vertices{P6,L,P11,L,P23,L,P24,L,P26,L}(through their redefined coefficients),are indirectly constraining from their one-loop contribution to the EWPD derived in Ref.[66],where it was shown that the five operators correct α∆T while render α∆S= α∆U=0.In Table 8 are reported the indirect bounds from Ref.[16]in terms of the implied redefined coefficients,that were determined via the oblique parameters in(57). On the other hand,anomalous QGC are directly testable at the LHC via three vector bosons production(V V V)or in vector boson fusion(VBF)production of two gauge bosons.[67]The best limits come out from the V V V-processes at lower center-of-mass energies,whilst the VBF channel dominates for the 14 TeV run.[67−71]For a 14 TeV at the LHC,the coefficientsandcan be constrained by their combined impact on the VBF channels pp→ jjW+W−and pp→ jj(W+W++W−W−),where j stands for a tagging jet and the final state W’s decay into electron or muon plus neutrino.In Ref.[69]were reported the 99%CL bounds on these coefficients as c6,L∈ [−0.012,0.01]and c11,L∈ [−0.0077,0.014],for an integrated luminosity of 100 fb−1.These limits are not significantly improved after including the pp→jjZZ channel.[70] It is worthwhile to comment that for the hypothetical scenario of no LH operators,but only RH and the mixing LRH ones,there will be still contributions to the aforementioned couplings.This is due to the fact that low energy LH operators are effectively turned on once the RH gauge fields are integrated out,feature that is directly reflected in Table 1. Notice that no extra operators contribute in the hierarchical case to the coefficients in Table 8.Additional terms contribute to them for a non-small parameter ϵ and a mixing coefficient cC,LR∼O(1)though.NP effects not far above from the EW scale would point towards a nonsmall ratio ϵ≡ fL/fR,feature that seems to be favoured by the diboson excess observed at LHC.Such excesses and the impact they entail in our scenario will be analysed in the next. Table 8 90%CL bounds on the anomalous QGC from their1-loop contribution tothe EWPD.[16]assuming only one non-zero operator at a time and for a cuto ffΛs=2 TeV. Tantalizing deviations from the SM predictions have been recently reported by the ATLAS and CMS Collaborations around invariant mass of(1.8–2)TeV.They can be interpreted via a W′contribution,and are summarized as: (a)3.4σ local(2.5σ global)excess in the ATLAS search[72](CMS reports a slight excess at the same mass[73])for a heavy resonance W′decaying as W′→WZ→JJ,where J stands for two colinear jets from a W or Z-boosted decay; (b)2.8σ excess in the CMS search[74]for a heavy RH boson W′decaying into an electron and RH neutrino N,as W′→N e→eejj; (c)A 2.2σ excess in the CMS search[75]for W′→ Wh,with a highly boosted SM Higgs boson h decaying as h → b¯b and W → ℓν (with ℓ=e,µ); (d)A 2.1σ excess in the CMS dijet search.[76] Many scenarios have been proposed in order to account for such excesses. Among them,the left-right EW symmetric model,based on the gauge group G=SU(2)L×SU(2)R×U(1)B−L,[6−7]seems to address properly the observed excesses in all the mentioned decay channels.Indeed,the WZ excess(item a)and Wh excess(item c)can be tackled[31,77−78]via W′→ WZ,Wh,as the implied couplings arise naturally in these models(see[79]for some alternative explanations of the diboson excess).The eejj excess(item b)can be understood[31,80−82]through the process pp→W′→N e→eejj,[83]and for a charged gauge boson mass MW′∼ 2 TeV,with gR It is straightforward to translate a W′-boson mass nearby(1.8–2)TeV,into our parameter space.Employing again the W′mass formula in(26),we obtain For a coupling gRin the range gR≈ 0.45–0.6[31]we find the SU(2)Rbreaking scale fR≈ (6–8)TeV,entailing thus a ratio ϵ≡ fL/fR≈ 0.03–0.04 for fLaround the EW regime.The small range for cC,LRin(39)leads then to a negligible parameter ¯ϵ∼ 10−4,suppressing as a consequence all the linear and higher¯ϵ-effects induced by the RH and LRH operators onto the LH ones,according with the redefined coefficients in Table 1.Such effects could be enhanced either via larger strength contributions from the custodial mixing LRH operator PC,LR(h),or via NP effects from the right handed gauge sector around the EW scale fL.The former scenario goes against the range in(39),spoiling thus the EW value in(38).The second possibility points towards ϵ∼ 1,then ¯ϵ∼ 0.02 for a strength contribution of PC,LR(h)around its maximal bound in(39),and triggering therefore linear¯ϵ-effects.In particular,all the LH operators sector in(12)and the LH basis in Appendix A1,will be sensitive to ¯ϵ-contributions from the LRH operators,whereas the operators P1,Land P4,Lwill have,in addition,extra¯ϵ-terms from some RH operators.This is schematically shown in Table 9,where the set of operators sensitive to the mentioned effects are collected for both of the¯ϵ-cases. As it was mentioned before for the bounds on the hV V couplings,the operators set{P7,L,P9,L,P10,L}wasnotincluded since theirphysicalimpact on the observables considered is negligible, while the set {P12,L,P17,L,P19,L,P25,L} entails no relevant contribution for the non-linear realization of the dynamics.[16]In addition, the operators set{P9,L,P10,L,P15,L,P16,L,P19−21,L}becomes redundant for the massless fermion case via EOM,[16]while the set{P8,L,P18,L,P20−22,L}does not contribute directly to any of the couplings listed previously. Consequently,when ¯ϵ is not negligible,the additional terms contributing to each one of these operators(LRH according to Table 1)can also be disregarded.From all these considerations it is concluded that the set of 20 LRH operators can be disregarded7Nonetheless the contributions from the P12(1),P13(2,4)and P17(2)enter also through P1,L,P2,Land P4,Lrespectively,being constrained then by the corresponding bounds on the latter LH operators.for a non-small parameter¯ϵ.By implementing the currents ranges that were obtained from EWPD bounds,TGC limits,hV V-couplings constrains and QGC bounds in Tables 5–8 respectively,it is possible to limit as well the additional emerging operators for a non-neglible¯ϵ via the redefined coefficients in Table 1.This is shown in Appendix D Table 10,where all the corresponding coefficients range for both of the RH or LRH operators are collected and compared with respect to those previously reported for the hierarchical case¯ϵ∼10−4.It is possible to conclude from Table 9 and the set in(63),that 7 RH operators and 23 LRH ones can be bounded through the obtained allowed ranges for the case of¯ϵ∼10−2. Table 9 LH operators(2nd row)sensitive to the RH and LRH operators(3rd and 4th rows)after removing the RH gauge field,and for both of the hierarchical case ¯ϵ∼ 10−4and ¯ϵ∼ 10−2(1st and 2nd big columns).The operators collected here follow the redefined coefficients in Table 1.A TeV-charged resonances accounting for the observed diboson excess points towards ¯ϵ∼ 10−4,and then 5 RH operators and 7 LRH ones contribute to 6 LH operators(1st big column&2nd row).NP effects from the right handed gauge sector around the EW scale fLfavours ϵ∼ 1,then ¯ϵ∼ 0.02,and consequently 7 RH operators and 43 LRH ones contribute now to 30 LH operators(2nd big column&2nd row). Table 10 The number of the most relevant set of non-linear LH,RH,and LRH operators for the three different ¯ϵ-scenarios. The hypothetical scenario of larger strength contributions from the operator PC,LR(h)(¯ϵ∼ 1),will drive all the RH and LRH operators in Appendixes A1 and A2 respectively,to contribute onto all the LH operators sector in(12)and the LH basis in Appendix A1.The following set of 12 RH8P12,R,P13,Rand P17,Renter through P1,L,P2,Land P4,Lrespectively,being then constrained by the corresponding bounds on the latter LH operators.and 27 LRH operators can be disregarded and being possible to constrain therefore 17 RH and 48 LRH operators.The corresponding coefficients range for the remaining operators are also gathered in Appendix D.Some remarks are in order: •The ranges for cT,Rand cT,LRare unmodified as they are insensitive to additional ¯ϵ-corrections(see Table 1). •The corresponding percent and 10%level ranges for{c1,R,c12,R,cW,LR}and{c3(2),c13(2)}respectively,become slightly modified for¯ϵ∼10−2with respect to the hierarchical case,reaching correspondingly a precision of the thousandth and percent level for the hypothetical case ¯ϵ∼ 1. •The ranges of order O(1−10)for{c4,R,c17,R}and{c5(1−2),c6(3),c11(3),c23(3,6)}when ¯ϵ∼ 10−2,become smaller and around the 10%level for¯ϵ∼1.Similarly,the ranges for{c2(1),c3(3−4)}turn out to be more precise and constrained at the percent level. •The ranges for c12(1)are all at the thousandth level,slightly modified for ¯ϵ∼ 10−2with respect to the hierarchical case,and becoming half of the range for¯ϵ∼1 compared with the one for¯ϵ∼10−4. All these remarks lead us therefore to establish the number of the most relevant set of non-linear LH,RH,and LRH operators for the three different scenarios in Table 10.In parentheses it has been pointed out the number of remaining operators after neglecting those ones with a corresponding coefficient bounded at the thousandth level.All the remaining operators can be easily identified by keeping track of their corresponding coefficients in Appendix D Table 11. An NP scenario is pictured in this work through,the existence of spin-1 resonances sourced by the extension of the SM local gauge symmetry GSM=SU(2)L×U(1)Yup to the larger local group G=SU(2)L×SU(2)R×U(1)B−L.Such scenario is described here via a non-linear EW dynamical Higgs scenario,and up to the p4-order in the Lagrangian expansion. A generic UV completion of the low energy non–linear treatment of Refs.[11–15]and Refs.[9,16]has been considered here via a non-linear left-right framework. Its physical impact has been analysed by integrating out the right handed gauge sector from the physical spectrum,leading the RH and the mixing LRH operators to collapse directly onto the LH sector,and inducing therefore corrections in all the effective pure gauge and gauge-Higgs couplings.These corrections are entirely parametrized in Table 1 via the weighting powers of¯ϵ≡ ϵcC,LR,with the scale ratio ϵ≡ fL/fRand the coefficient cC,LRencoding the strength of the contribution from the mixing operator PC,LR(h).This feature leads to modify,consequently,the EWPD parameters(Eqs.(50)–(51)),the TGC(Table 2),hV V-couplings(Table 4)and the anomalous QGC as well(Table 3).Corresponding allowed ranges for the involved coefficients have also been reported through Tables 5–8 respectively.In the hypothetical scenario of no LH operators,but only RH and the mixing LRH operators,there will be still contributions to the aforementioned couplings.This is due to the fact that low energy LH operators are effectively turned on once the RH gauge field sector is integrated out,feature that is directly re flected in Table 1. Table 11 Allowed ranges for both of the RH(upper row)and LRH operators(lower row),for ¯ϵ∼ 10−2(3rd and 7th columns),¯ϵ∼ 1(4th and 8th columns),compared with respect to those for the hierarchical case ¯ϵ∼ 10−4suggested by the diboson excess(2nd and 6th columns).The ranges were obtained via the redefined coefficients in Table 1,and implementing the 95%CL ranges from EWPD bounds,and the 90%CL limits from TGC,hV V-couplings and QGC constrains from Tables 5,6,7,and 8 respectively.One non-zero operator was assumed at a time. The recently observed diboson excess at the ATLAS and CMS Collaborations around the invariant mass of(1.8–2)TeV entails a scale fR∼ (6–8)TeV,leading to a negligible parameter¯ϵ∼10−4and suppressing therefore all the linear and higher ¯ϵ-effects induced by the RH and LRH operators.These effects could be enhanced either via larger strength contributions from the custodial mixing operator PC,LR(h),or via NP effects from the right handed gauge sector around the EW scale fLtogether with a strength contribution of PC,LR(h)around its maximal bound in(39).The former scenario spoils the EW value in(38),whereas the latter one points towards¯ϵ∼ 10−2.The set of relevant non-linear LH,RH,and LRH effective operators have been completely identified for the latter regimes and by disregarding:(i)irrelevant LH operators with negligible physical impact on the observables considered for the hV V–bounds,(ii)irrelevant operators for the non-linear realization of the dynamics and redundant for the massless fermion case;(iii)operators without any direct contribution to the pure gauge and gauge-Higgs couplings listed above. The hypothetical case of larger strength contributions from PC,LR(h)would point towards¯ϵ∼1,enhancing therefore additional contributions from the RH and LRH operators,and required thus an effective basis of 77 operators in total=12 LH+17 RH+48 LRH(or 62 neglecting irrelevant ones=9 LH+12 RH+41 LRH).The small range for cC,LRleads to¯ϵ∼10−2,requiring thus a smaller number of effective operators of 42 operators=12+7+23(or 36 without irrelevant ones=9+6+21).The diboson excess around the invariant mass(1.8–2)TeV entails a suppression of¯ϵ∼10−4,and therefore the low energy effects will be encoded via a much smaller effective basis with 29 operators in total=17+5+7(or 18 relevant=9+4,+5).The set of remaining operators are identified by their corresponding coefficients in Table 10.A more detailed interpretation of the diboson excess it is also possible via the left-right non-linear Higgs approach studied here and it can be found in Ref.[33]. Acknowledgements The authors of this work acknowledge valuable and enlightening comments from J.Gonzalez–Fraile. Appendix A:Operators List A1G-extension ofL0+L0,R:∆LCP The complete linearly independent set of 26 CP–conserving pure gauge and gauge-h non-linear G-invariant operators up to the p4-order in the effective Lagrangian expansion,and encoded by Pi,L(h)( first term in the second line of∆LCP,L,Eq.(10))have completely been listed in Refs.[9,16].The symmetric counterpart Pi,R(h)(second term in∆LCP,Rof Eq.(11)),are 52 non-linear operators in total,among them,38(19 Pi,L(h)+19 Pi,R(h))had already been listed in Refs.[17–18].The whole tower of operators making up the basis{Pi,L(h),Pi,R(h)}is: A2 SU(2)L-SU(2)RInterplay:∆LCP,LR The local rotations induced by the group G are The adjoint vectorial and scalar quantitiesand TL(R)behave covariantly under the transformations in(69)as Therefore,the introduced objects in(8)will correspondingly behave as allowing thus to construct out explicit operators mixing the left-right handed covariant structuresand TL(R). Similar reasoning applies for the strength gauge fieldsIn here are listed the operators Pi(j),LR(h)(second term Eq.(14))where the index j spans over all the possible operators that can be built up from each Pi,χ(h)in Eqs.(66)–(67)(with associated coefficients ci(j),LR).The complete set of operators Pi(j),LR(h)listed as: Appendix B:Equations of Motion Considering the LO Lagrangian L0+L0,Rdescribed along Eqs.(4)–(5),and accounting for the mixing effects from the LRH operators PC,LR(h)and PW,LR(h)in(15)(the effect of PT,LR(h)can be neglected),the EOM for the strength gauge fieldsand Bµ,and for the light Higgs h,are correspondingly where the fermion dependent part of the EOMs has been generically encoded in the third,second,and third terms at the first lines of Eqs.(75)–(77)respectively,as no explicit kinetic fermion terms nor Yukawa interactions were accounted by Lchiralin(3).From Eqs.(75)–(76)it is derived where the last terms in Eqs.(78)–(79)can be translated into Yukawa terms via implementation of the corresponding Dirac equations.As it can be seen from the relations above,operators containing the contractioncan be translated into fermionic-bosonic operators plus pure bosonic ones,with some of them containing the contraction(from the second terms in the left hand side of Eqs.(78)–(79).Furthermore,by using the light Higgs-EOM in Eq.(77),those operators with two derivative couplings of F(h)can be also rewritten in terms of pure bosonic ones plus fermionic-bosonic ones. Appendix C:(De)correlation Formulae Some of the non–linear operators in(10),(11)and(14)contribute to more than one of the couplings in Tables 2–4.Therefore,a set of relations relating different couplings are possible.For the TGV sector one has while other examples of relations involving hV V-couplings are where the variations in the left hand side of(80)and(83)–(85)are corresponding in this scenario to the sum of the values at the 3rd and 4th columns in Tables 2–4.The induced effects encoded through αWBcancels out in(80).By linking non-linear approaches to the linear effective scenarios explicitly implementing the SM Higgs doublet,[9,16]and via powers of the weighting parameter,it is realized that the right-hand side of Eqs.(80)–(85)correspond to v-weighted terms in the non-linear Lagrangian.They would vanish if:(i)the d=6 linear limit9Eq.(80)with vanishing right-hand side was already known to hold in the linear regime at d=6.[85−88];(ii)in the v-truncated non-linear Lagrangian;(iii)in the custodial preserving limit.The first two relations with a vanishing right-hand side where already found in Ref.[84].Non-zero deviations from zero in the data combinations indicated by the left-hand side of those equations would point towards either d=8 corrections of the linear expansion or a non-linear realisation of the underlying dynamics. Appendix D:Operator Coefficients Bounds By implementing the currents ranges that were obtained from EWPD bounds,TGC limits,hV V-couplings constrains and QGC bounds in Tables 5–8 respectively,it is possible to limit as well the additional emerging operators for a non-neglible¯ϵ via the redefined coefficients in Table 1.Table 10 collects all the corresponding coefficients ranges for both of the RH and LRH operators. [1]ATLAS Collaboration Collaboration,G.Aad,et al.,Phys.Lett.B 716(2012)1. [2]CMS Collaboration Collaboration,S.Chatrchyan,et al.,Phys.Lett.B 716(2012)30. [3]F.Englert and R.Brout,Phys.Rev.Lett.13(1964)321. [4]P.W.Higgs,Phys.Lett.12(1964)132. [5]P.W.Higgs,Phys.Rev.Lett.13(1964)508. [6]J.C.Pati and A.Salam,Phys.Rev.D 10(1974)275. [7]R.N.Mohapatra and J.C.Pati,Phys.Rev.D 11(1975)566;R.N.Mohapatra and J.C.Pati,Phys.Rev.D 11(1975)2558;G.Senjanovic and R.N.Mohapatra,Phys.Rev.D 12(1975)1502. [8]H.Georgi and D.B.Kaplan,Phys.Lett.B 145(1984)216. [9]R.Alonso,M.B.Gavela,L.Merlo,S.Rigolin,and J.Yepes,Phys.Lett.B 722(2013)330. [10]J.Yepes,arXiv:1507.03974[hep-ph]. [11]T.Appelquist and C.W.Bernard,Phys.Rev.D 22(1980)200. [12]A.C.Longhitano,Phys.Rev.D 22(1980)1166. [13]A.C.Longhitano,Nucl.Phys.B 188(1981)118. [14]F.Feruglio,Int.J.Mod.Phys.A 8(1993)4937. [15]T.Appelquist and G.H.Wu,Phys.Rev.D 48(1993)3235. [16]I.Brivio,T.Corbett,O.J.P.boli,et al.,J.High Energy Phys.1403(2014)024. [17]Y.Zhang,S.Z.Wang,F.J.Ge,and Q.Wang,Phys.Lett.B 653(2007)259. [18]S.Z.Wang,S.Z.Jiang,F.J.Ge,and Q.Wang,J.High Energy Phys.0806(2008)107. [19]K.M.Ruan,J.Shu,and J.Yepes,Commun.Theor.Phys.66(2016)93. [20]M.B.Gavela,J.Gonzalez–Fraile,M.C.Gonzalez–Garcia,et al.,J.High Energy Phys.1410(2014)44. [21]R.Alonso,M.B.Gavela,L.Merlo,S.Rigolin,and J.Yepes,Phys.Rev.D 87(2013)055019. [22]G.Buchalla,O.Cata,and C.Krause,Nucl.Phys.B 880(2014)552. [23]G.Buchalla and O.Cat`a,J.High Energy Phys.1207(2012)101. [24]G.Buchalla,O.Cata,and C.Krause,Phys.Lett.B 731(2014)80. [25]I.Brivio,arXiv:1505.00637[hep-ph]. [26]G.Cvetic and R.Kogerler,Nucl.Phys.B 328(1989)342. [27]R.Alonso,M.Gavela,L.Merlo,S.Rigolin,and J.Yepes,J.High Energy Phys.1206(2012)076. [28]G.F.Giudice,C.Grojean,A.Pomarol,and R.Rattazzi,J.High Energy Phys.06(2007)045. [29]G.Buchalla,O.Cata,and C.Krause,Nucl.Phys.B 894(2015)602. [30]I.Brivio,M.B.Gavela,L.Merlo,K.Mimasu,J.M.No,R.del Rey,and V.Sanz,J.High Energy Phys.1604(2016)141. [31]B.A.Dobrescu and Z.Liu,Phys.Rev.Lett.115(2015)211802;J.High Energy Phys.1510(2015)118. [32]V.Khachatryan,et al.,[CMS Collaboration],Phys.Rev.D 91(2015)052009. [33]J.Shu and J.Yepes,arXiv:1601.06891[hep-ph]. [34]Particle Data Group Collaboration,J.Beringer,et al.,Phys.Rev.D 86(2012)010001. [35]ATLAS Collaboration,G.Aad,et al.,Phys.Lett.B 716(2012)1. [36]CMS Collaboration,S.Chatrchyan,et al.,Phys.Lett.B 716(2012)30. [37]M.E.Peskin and T.Takeuchi,Phys.Rev.Lett.65(1990)964. [38]K.Hagiwara,R.Peccei,D.Zeppenfeld,and K.Hikasa,Nucl.Phys.B 282(1987)253. [39]F.Feruglio and S.Rigolin,Phys.Lett.B 397(1997)245. [40]The LEP Collaborations and the LEP TGC Working group,Tech.Rep.LEPEWWG/TGC/2003-01. [41]OPAL Collaboration,G.Abbiendi,et al.,Eur.Phys.J.C 33(2004)463. [42]L3 Collaboration,P.Achard,et al.,Phys.Lett.B 586(2004)151. [43]ALEPH Collaboration,S.Schael,et al.,Phys.Lett.B 614(2005)7. [44]O.J.Eboli,S.Lietti,M.Gonzalez-Garcia,and S.Novaes,Phys.Lett.B 339(1994)119. [45]S.Dawson and G.Valencia,Phys.Lett.B 333(1994)207. [46]O.J.Eboli,M.Gonzalez-Garcia,and S.Novaes,Mod.Phys.Lett.A 15(2000)1. [47]B.Tuchming,et al.,[D0 and CDF Collaborations],EPJ Web Conf.60(2013)02003. [48]ATLAS Collaboration,Tech.Rep.ATLAS-CONF-2012-160,CERN,Geneva,Nov.(2012). [49]ATLAS Collaboration,Tech.Rep.ATLAS-CONF-2013-079,CERN,Geneva,Jul.(2013). [50]ATLAS Collaboration,Tech.Rep.ATLAS-CONF-2013-013,CERN,Geneva,Mar.(2013). [51]ATLAS Collaboration,Tech.Rep.ATLAS-CONF-2012-030,CERN,Geneva,Mar.(2012). [52]ATLAS Collaboration,Tech.Rep.ATLAS-CONF-2012-091,CERN,Geneva,Mar.(2013). [53]ATLAS Collaboration,Tech.Rep.ATLAS-CONF-2013-012,CERN,Geneva,Mar.(2013). [54]CMS Collaboration,Tech.Rep.CMS-PAS-HIG-13-004,CERN,Geneva(2013). [55]CMS Collaboration,Tech.Rep.CMS-PAS-HIG-13-012,CERN,Geneva(2013). [56]CMS Collaboration,Tech.Rep.CMS-PAS-HIG-13-011,CERN,Geneva(2013). [57]CMS Collaboration,Tech.Rep.CMS-PAS-HIG-13-002,CERN,Geneva(2013). [58]CMS Collaboration,Tech.Rep.CMS-PAS-HIG-13-003,CERN,Geneva(2013). [59]CMS Collaboration,Tech.Rep.CMS-PAS-HIG-13-001,CERN,Geneva(2013). [60]S.Chatrchyan,et al.,[CMS Collaboration],Phys.Lett.B 726(2013)587. [61]T.Corbett,O.Eboli,J.Gonzalez-Fraile,and M.Gonzalez-Garcia,Phys.Rev.D 86(2012)075013. [62]T.Corbett,O.Eboli,J.Gonzalez-Fraile,and M.Gonzalez-Garcia,Phys.Rev.Lett.111(2013)011801. [63]T.Corbett,O.J.P.Eboli,D.Goncalves,J.Gonzalez-Fraile,T.Plehn,and M.Rauch,arXiv:1511.08188[hepph]. [64]CMS Collaboration,arXiv:1307.7135[hex-ex]. [65]ATLAS Collaboration,arXiv:1307.7292[hex-ex]. [66]A.Brunstein,O.J.Eboli,and M.Gonzalez-Garcia,Phys.Lett.B 375(1996)233. [67]O.J.Eboli,M.Gonzalez-Garcia,S.Lietti,and S.Novaes,Phys.Rev.D 63(2001)075008. [68]O.Eboli,M.Gonzalez-Garcia,and S.Lietti,Phys.Rev.D 69(2004)095005. [69]O.Eboli,M.Gonzalez-Garcia,and J.Mizukoshi,Phys.Rev.D 74(2006)073005. [70]A.S.Belyaev,O.J.P.Eboli,M.C.Gonzalez-Garcia,et al.,Phys.Rev.D 59(1999)015022. [71]C. Degrande, J. Holzbauer, S.C. Hsu, et al.,arXiv:1309.7452[physics.comp-ph]. [72]G.Aad,et al.,[ATLAS Collaboration],J.High Eenergy Phys.1512(2015)055;Eur.Phys.J.C 75(2015)69;Eur.Phys.J.C 75(2015)209. [73]V.Khachatryan,et al.,[CMS Collaboration],J.High Eenergy Phys.1408(2014)173;J.High Eenergy Phys.1408(2014)174. [74]V.Khachatryan,et al.,[CMS Collaboration],Eur.Phys.J.C 74(2014)3149. [75]CMS Collaboration,CMS-PAS-EXO-14-010(2015). [76]V.Khachatryan,et al.,[CMS Collaboration],Phys.Rev.D 91(2015)052009;G.Aad,et al.,[ATLAS Collaboration],Phys.Rev.D 91(2015)052007. [77]J.Hisano,N.Nagata,and Y.Omura,Phys.Rev.D 92(2015)055001;K.Cheung,W.Y.Keung,P.Y.Tseng,and T.C.Yuan,Phys.Lett.B 751(2015)188;Y.Gao,T.Ghosh,K.Sinha,and J.H.Yu,Phys.Rev.D 92(2015)055030;Q.H.Cao,B.Yan,and D.M.Zhang,Phys.Rev.D 92(2015)095025;T.Abe,T.Kitahara,and M.M.Nojiri,J.High Energy Phys.1602(2016)084;A.E.Faraggi and M.Guzzi,Eur.Phys.J.C 75(2015)537. [78]J.Brehmer,J.Hewett,J.Kopp,T.Rizzo,and J.Tattersall,J.High Eenergy Phys.1510(2015)182. [79]J.A.Aguilar-Saavedra,J.High Eenergy Phys.1510(2015)099;A.Thamm,R.Torre,and A.Wulzer,Phys.Rev.Lett.115(2015)221802;A.Carmona,A.Delgado,M.Quirs,and J.Santiago,J.High Energy Phys.1509(2015)186;Y.Omura,K.Tobe,and K.Tsumura,Phys.Rev.D 92(2015)055015;L.Bian,D.Liu,and J.Shu,arXiv:1507.06018[hep-ph];P.Arnan,D.Espriu,and F.Mescia,Phys.Rev.D 93(2016)015020;H.M.Lee,D.Kim,K.Kong,and S.C.Park,J.High Eenergy Phys.1511(2015)150;B.C.llanach,P.S.B.Dev and K.Sakurai,Phys.Rev.D 93(2016)035010;D.Aristizabal Sierra,J.Herrero-Garcia,D.Restrepo,and A.Vicente,Phys.Rev.D 93(2016)015012;J.A.Aguilar-Saavedra and F.R.Joaquim,J.High Eenergy Phys.1601(2016)183;J.de Blas,J.Santiago and R.Vega-Morales,Phys.Lett.B 759(2016)247;A.Sajjad,Phys.Rev.D 93(2016)055028;P.S.Bhupal Dev and R.N.Mohapatra,Phys.Rev.Lett.115(2015)181803;F.F.Deppisch,L.Graf,S.Kulkarni,et al.,Phys.Rev.D 93(2016)013011;A.Berlin,Phys.Rev.D 93(2016)055015;A.Das,N.Nagata,and N.Okada,J.High Eenergy Phys.1603(2016)049. [80]F.F.Deppisch,T.E.Gonzalo,S.Patra,N.Sahu,and U.Sarkar,Phys.Rev.D 90(2014)053014;Phys.Rev.D 91(2015)015018. [81]M.Heikinheimo,M.Raidal,and C.Spethmann,Eur.Phys.J.C 74(2014)3107;J.A.Aguilar-Saavedra,and F.R.Joaquim,Phys.Rev.D 90(2014)115010;A.Fowlie and L.Marzola,Nucl.Phys.B 889(2014)36;M.E.Krauss and W.Porod,Phys.Rev.D 92(2015)055019. [82]J.Gluza and T.Jeliński,Phys.Lett.B 748(2015)125. [83]W.Y.Keung and G.Senjanović,Phys.Rev.Lett.50(1983)1427. [84]R.Contino,M.Ghezzi,C.Grojean,M.Muhlleitner,and M.Spira,J.High Energy Phys.1307(2013)035. [85]K.Hagiwara,S.Ishihara,R.Szalapski,and D.Zeppenfeld,Phys.Rev.D 48(1993)2182. [86]K.Hagiwara,S.Matsumoto,and R.Szalapski,Phys.Lett.B 357(1995)411.2.2 Integrating-out Heavy Right Handed Fields
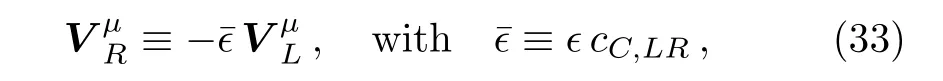



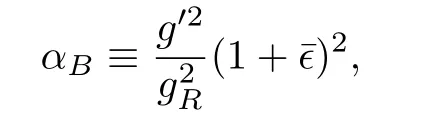
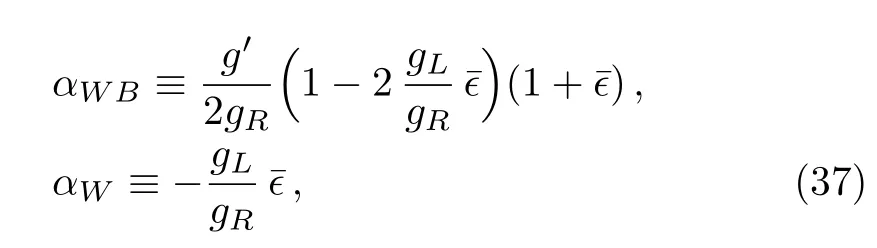






3 Low Energy Phenomenology
3.1 Renormalization Scheme






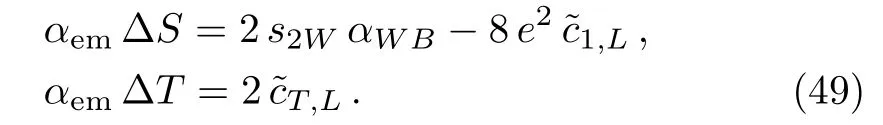


3.2 Triple Gauge-Boson Couplings



3.3 Quartic Gauge-Boson Couplings
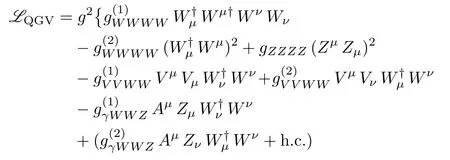


3.4 Triple Gauge-h Couplings
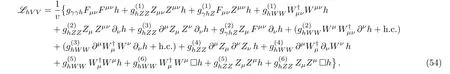
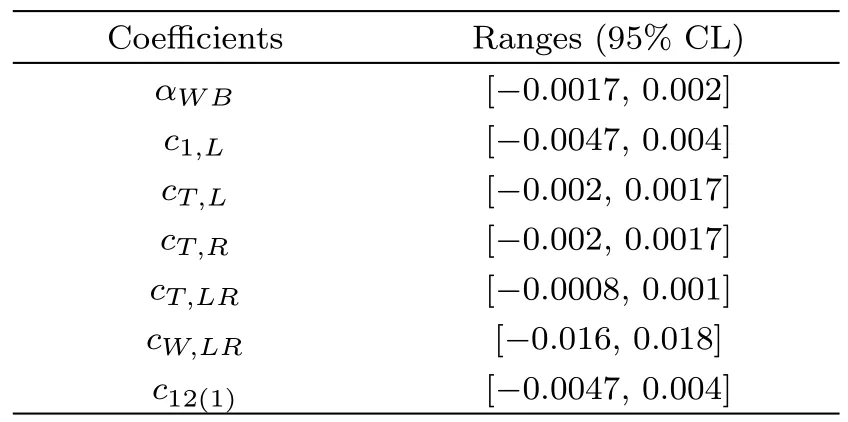
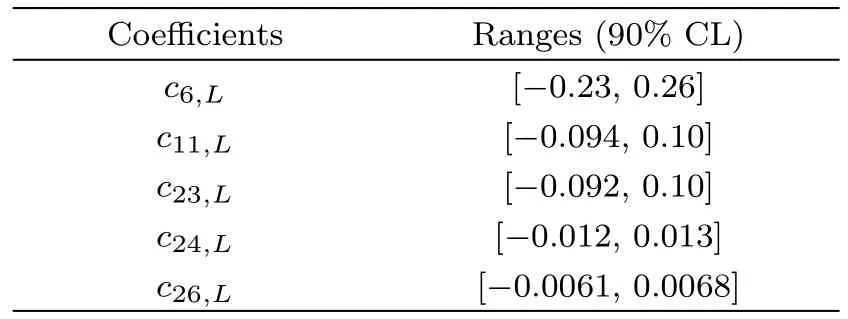
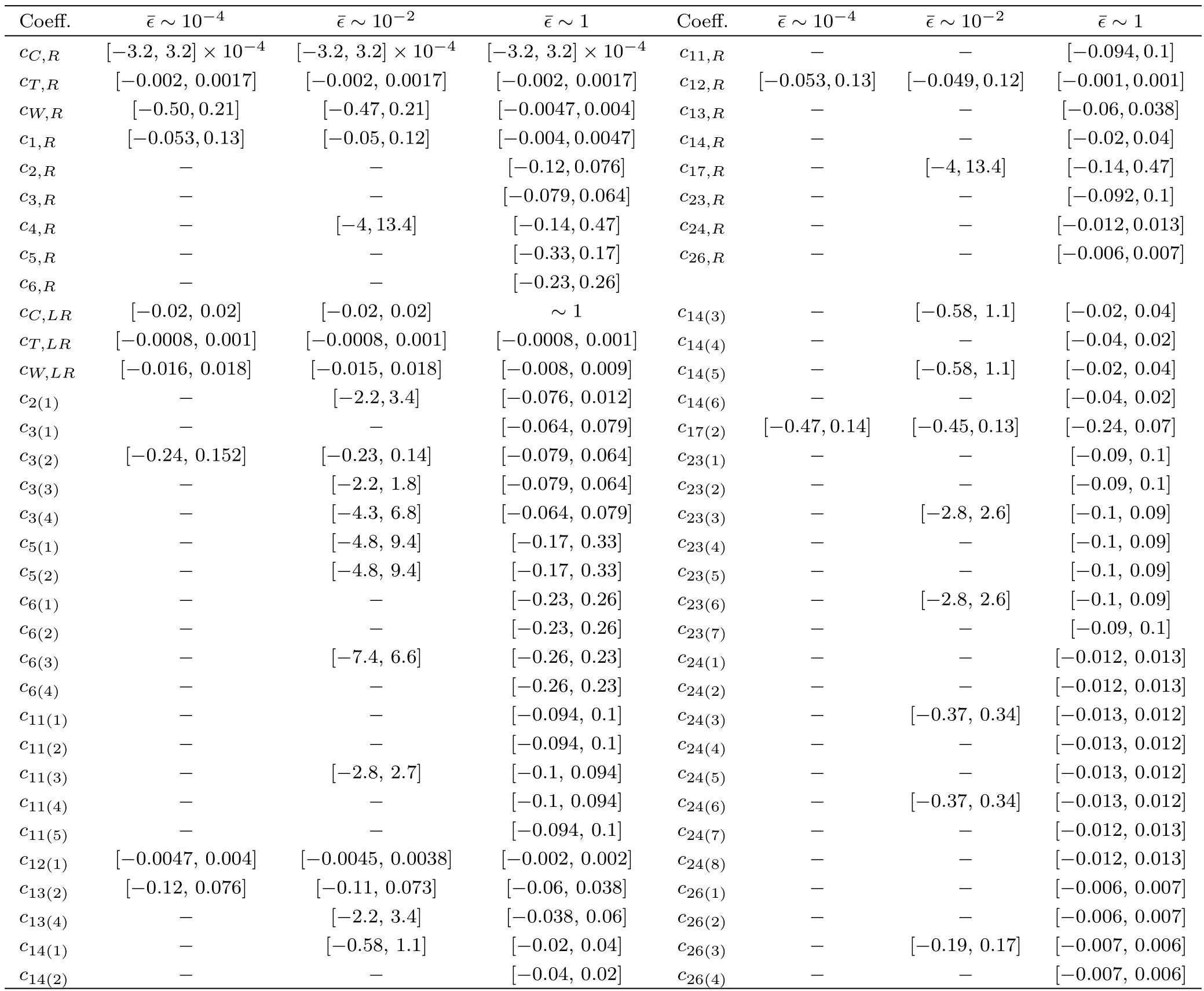
3.5 Current Operators Bounds

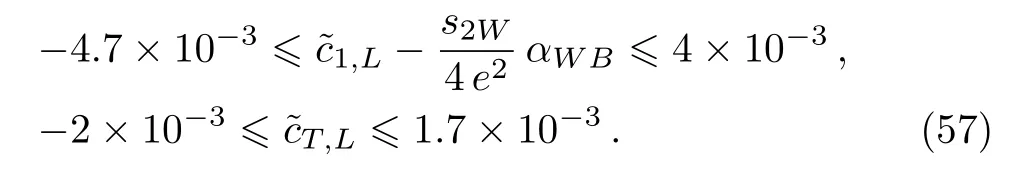
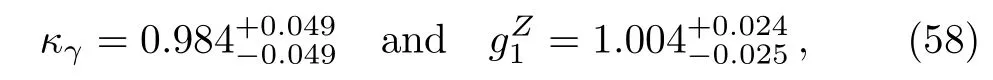





4 Comments on the Diboson Excess at LHC





5 Conclusions




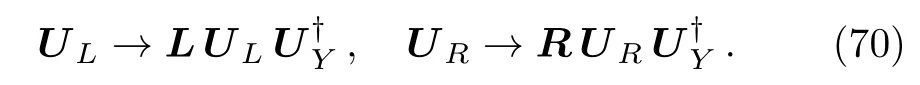

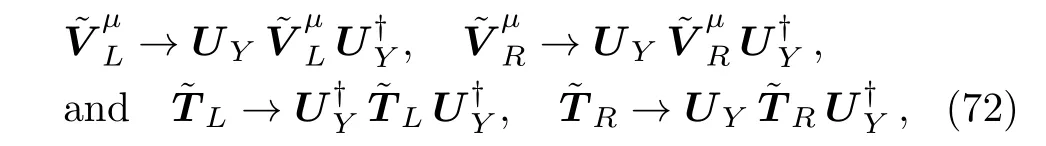





杂志排行
Communications in Theoretical Physics的其它文章
- Pressure Oscillating Flow in Corrugated Parallel Channel∗
- The Role of a1(1260)in π−p →(1260)p and π−p → π−ρ0p Reactions Near Threshold∗
- Dilepton from Passage of Jets Through Spherical Expanding QGP∗
- Free Convective Nonaligned Non-Newtonian Flow with Non-linear Thermal Radiation
- Weibel Instability Growth Rate in Magnetized Plasmas with Quasi-Relativistic Distribution Function
- Quantum Private Comparison of Equality Based on Five-Particle Cluster State∗
