Free Convective Nonaligned Non-Newtonian Flow with Non-linear Thermal Radiation
2016-05-09RanaMehmoodPVNarayanaandAkbar
S.Rana,R.Mehmood,PV S.Narayana,and N.S.Akbar
1Department of Mathematics,Faculty of Natural Sciences,HITEC University,Taxila Cantt,Pakistan
2Department of Mathematics,VIT University,Vellore,India
3National University of Sciences and Technology(NUST),Islamabad,44000,Pakistan
1 Introduction
In recent years rapid development has been made in the study of mixed convective non-orthogonal flows of some non-Newtonian fluids due to their abundant applications in engineering and industrial technologies.[1−9]Stagnation-point flow is of worth importance because these points seem in all types of flows in industrial and science technology,sometimes they are stagnated by some solid surface and sometimes by an unrestricted line exist inside the domain of fluid.Such type of flows might be categorized as time dependent or independent,viscid or in viscid,symmetric or asymmetric,they can be two or three-dimensional,orthogonal and non-orthogonal.Twodimensional stagnation point flow acts through an inclined angle on some fixed surface.These types of flows attracted the attention of numerous researchers in past few decades.Lok et al.[10]investigated tilted stagnation point flow over a stretched surface.Nadeem et al.[11]examined stagnation point boundary layer flow analytically by HAM.Robert et al.[12]studied hydro magnetic viscid stagnation point flows towards a stretching or shrinking slip.Nadeem et al.[13]discussed axisymmetric stagnation point flow of a micro polar nano fluid in a moving cylinder and oblique stagnation point flows with heat transmission of a nano non-Newtonian fluid towards a stretched wall.[14]Some recent studies related to such type of flows may be found in Refs.[15–22].Casson fluid model is one of the most enticed models which is discussed with several physical effects such as magnetic field and slip conditions.[23−27]Mixed convective stagnation point streams are of vital importance.When temperature variance among two surfaces and free stream develops then buoyancy forces arises.They amend thermal fields and flows expressively.In these flows,local heat transmission and skin friction can be expressively boosted or reduced in contrast to pure forced convection case.This consequently increases or decreases heat transfer rate.Vajravellu[28]discussed heat transmission over a convective stretched sheet in an electrically conducting fluid.Bhattacharyya et al.[29]inspected convective heat transfer over a stretched sheet in an electrically conducting fluid.Some more useful studies related to current topic can be found in Refs.[30–33].
Thermal radiation plays a vital role in engineering and space technology where the operations are performed at very high temperatures.Heat transfer phenomena are controlled by thermal radiation in polymer manufacturing.Thus with the effect of thermal radiation the required quality of final product can be achieved.Nadeem et al.[34]discovered the effects of thermal radiation in an exponentially stretching sheet of a Jeffery fluid.Mukhopadhyay et al.[35]conferred forced convective flow in the presence of thermal radiation.Hashim et al.[36]analysed heat and mass transfer over an inclined radioactive porous surface with internal heating.Chamkha et al.[37]deliberated radiation effects on mixed convective flow over a wedge embedded in a permeable surface with a nano fluid.Pop et al.[38]discussed the properties of heat and mass transfer flow of nano fluids over a vertical in finite flat plate with thermal radiation.Sheikholeslami et al.[39]heat transfer flow of nano fluid on a porous extended surface and thermal radiation effects and later on examined the heat transfer by means of two phase model on magneto hydrodynamic nano fluid.[40]Some valuable discussions helpful to present theme may be debated in Refs.[[41–44].
The aim of present study is to discuss Natural convection on oblique Casson fluid over a stretching sheet with non-linear thermal radiation effects.To the best of our knowledge this kind of study has not been reported before.
2 Problem Formulation
Consider a steady,2D incompressible stagnation point flow of a Casson fluid on a stretched wall.To keep the wall stretched and origin fixed,a balance force is applied in the x-direction as shown in Fig.1.The basic steady conservation of mass,momentum and energy equation with nonlinear thermal radiation by neglecting viscous dissipation can be written as[6]
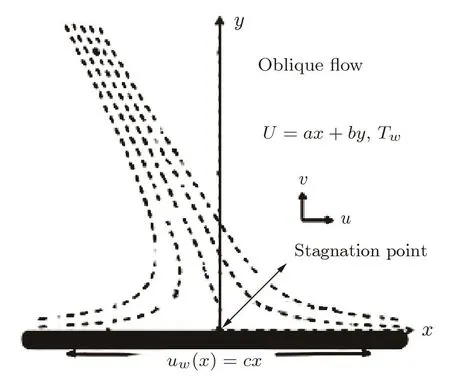
Fig.1 Physical description of the problem.
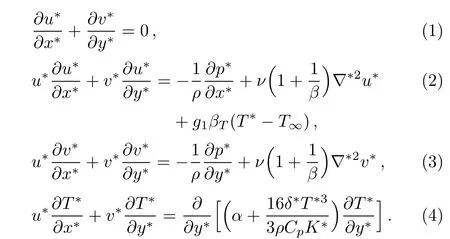
The corresponding boundary conditions for the problem are
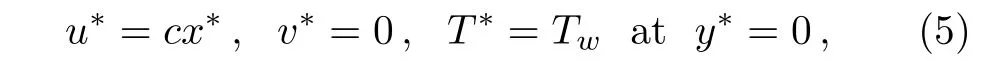

where u∗and v∗are the x-and y-components of velocity respectively,ν is the effective kinematic viscosity,p∗is the pressure,ρ is the density,T∗is the temperature,β is the Casson fluid parameter,βTis the thermal expansion coefficient,g1is the acceleration due to gravity,α =k/ρCpis thermal diffusivity,δ∗is the Stefan–Boltzmann constant and K∗is the mean absorption coefficient,Cpis specific heat at constant temperature,Twis the constant temperature of the wall,T∞is the ambient fluid temperature and a,b,c are the constants having dimension of inverse time.
Introducing similarity transformation[6]

Using Eq.(7),the set of Eqs.(1)–(6)in nondimensional form are

where
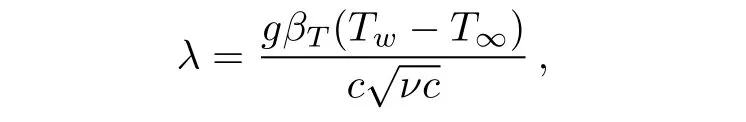
is the forced convection parameter,R=Tw/T∞is temperature ratio parameter and γ=b/c,represent obliqueness of the flow.
Introducing the stream function relations as[6]
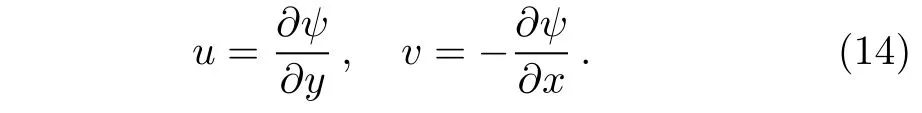
Using Eq.(14)the set of Eqs.(8)–(13)takes the form

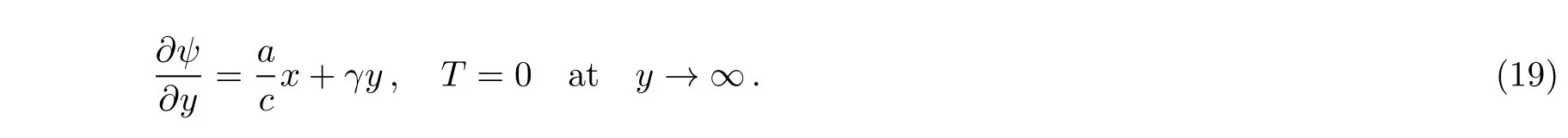
Eliminating pressure p using the fact that pxy=pyx,from Eqs.(15)and(16),we get

Redefining the stream function as[6]
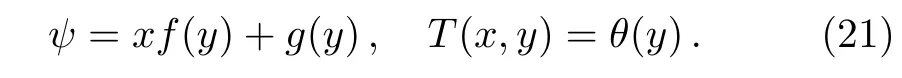
Using Eq.(21)in Eqs.(17)–(20)we get the following system of non-linear ordinary differential equations after integrating once
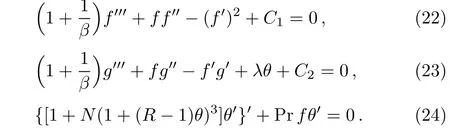
The corresponding boundary conditions take the form
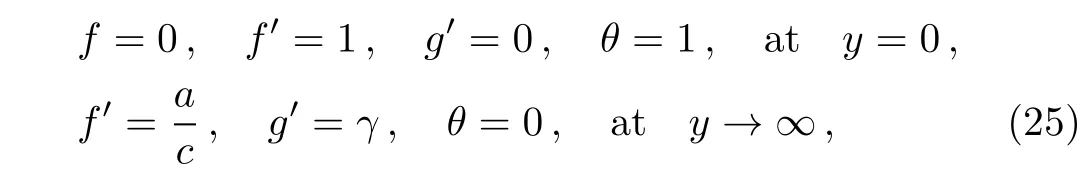
where C1and C2are constants of integration,N =is radiation parameter,Pr= ν/α is Prandtl number.
Making use of Eq.(25)in Eqs.(22)–(23),we get

Thus Eqs.(22)–(23)take the form
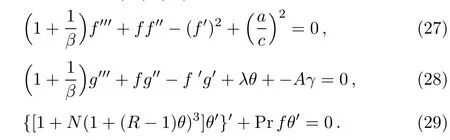
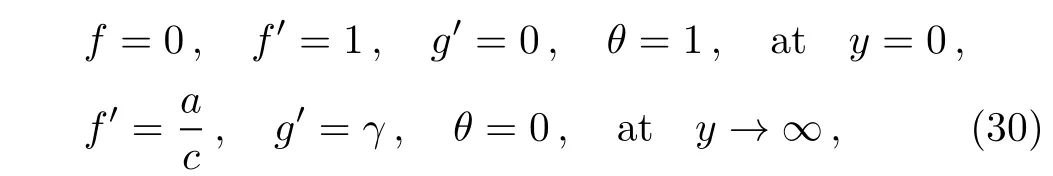
where prime denotes differentiation with respect to y.
3 Physical Quantities of Interest
Physical magnitudes of concern are tangential stress at surface and the local heat flux that can be defined as
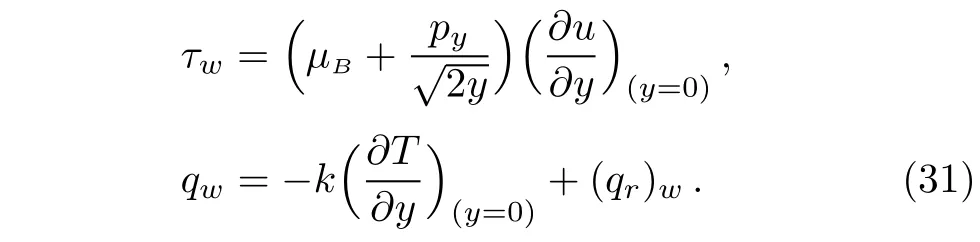
Along with boundary conditions
It can be written as in non-dimensional form

The stagnation point xscan be obtained by zero wall shear stress,i.e.
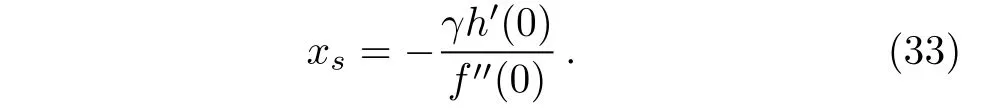
4 Numerical Solution
The governing system of Eqs.(27)–(29)along with boundary conditions(30)are coupled and nonlinear in nature,which are solved by using shooting method.The governing non-linear higher order differential equations are first transformed into system of first order non-linear ordinary differential equations,which are then solved by Runge-kutta Fehlberg method along with shooting technique.
Introducing the following substitutions in system of Eqs.(27)–(29),
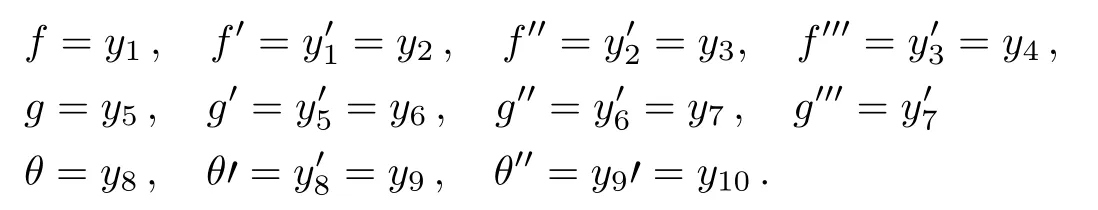
We have the following system of first order ordinary differential equations along with Initial conditions
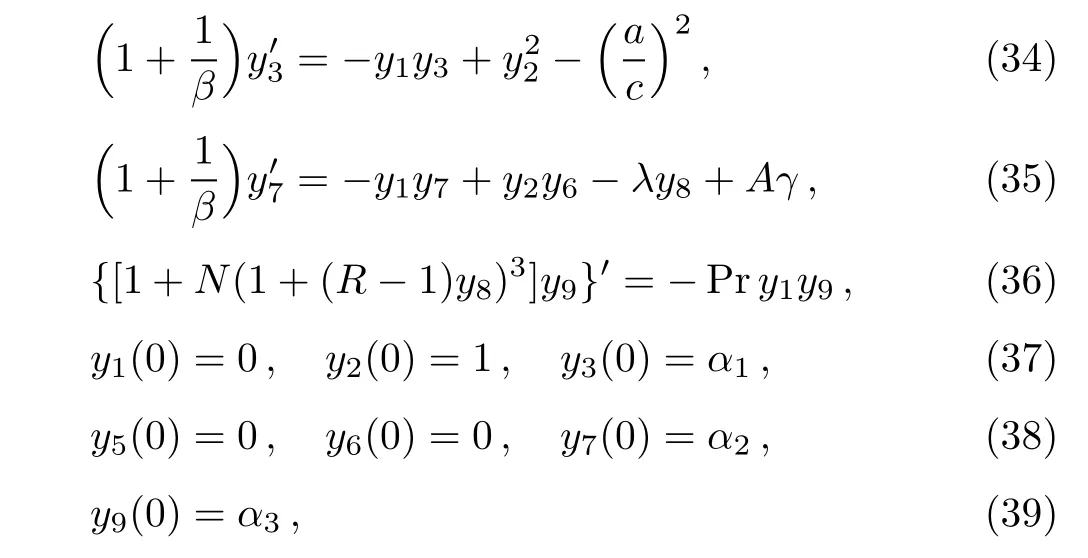
where α1, α2,and α3are shooting parameters.
A mesh size of 0.000 01 was supposed suitable for a convergence criterion of 10−6in all computations.
5 Results and Discussion
In this section the flow behaviour against some concerned physical constraints has been discussed.Figures 2–17 are plotted to meet the purpose.These graphs are plotted to find out the effects of stretching ratio a/c,Casson fluid parameter β,forced convection parameter λ,Prandtl number Pr,temperature ratio parameter R and Radiation parameter N on normal and tangential velocity components f′(y),g′(y)and temperature θ(y).Figure 2 depicts velocity pro file f′(y)against Casson fluid parameter β.We can see that with an increase in Casson fluid parameter β,normal component of velocity f′(y)and momentum boundary layer thickness decreases.In Figs.3–6 tangential component of velocity g′(y)grows with the rise in convection parameter λ,temperature ratio parameter R and Radiation parameter N,but decreases with increase in Prandtl number Pr.The behaviour of temperature θ(y)against relevant flow parameters is expressed through Figs.7–10.It can be observed that temperature θ(y)and thermal boundary layer thickness rises with an increase in Casson fluid parameter β,temperature ratio R,and Radiation parameter N but decreases with an increase in Prandtl number Pr.Figures 11–17 reveal the nature of skin friction coefficient g′′(0)and heat transfer coefficient θ′(0).Figure 11 is plotted against Casson fluid parameter β for different values of forced convection parameter λ tangential skin friction coefficient g′′(0).It is observed that for large values of mixed convection the tangential skin friction coefficient g′′(0)decreased.In Figs.12 and 13 tangential skin friction coefficient g′′(0)increase and decrease for growth of Casson fluid parameter β against radiation parameter N and Prandtl number Pr respectively.Wall temperature gradient θ′(0)is expressed through graphs against Casson fluid parameter β,mixed convection parameter λ,Prandtl number Pr,and temperature ratio parameter R in Figs.14–17.We see that wall temperature gradient θ′(0)increases for stretching ratio near the wall but away from the wall its behaviour is reversed.It is also observed that temperature gradient grows for the rise in Prandtl number Pr,radiation parameter N and temperature ratio parameter R respectively.

Fig.2 Behaviour of f ′(y)for β.
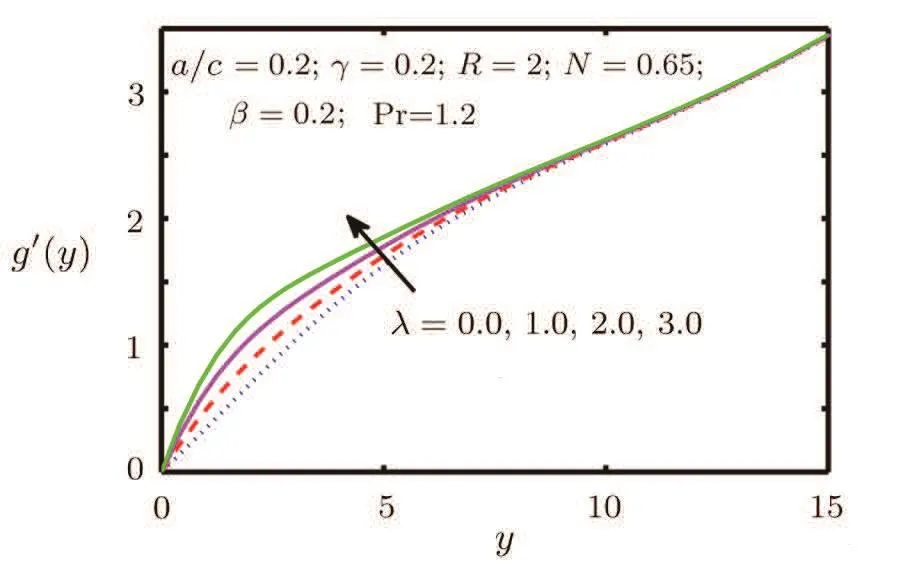
Fig.3 Behaviour of g′(y)for λ.
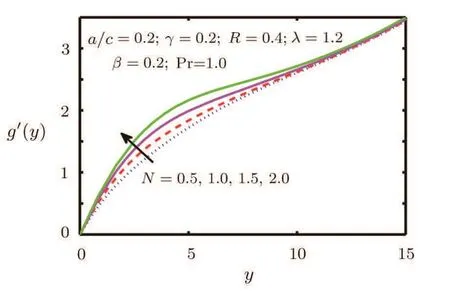
Fig.4 Behaviour of g′(y)for N.
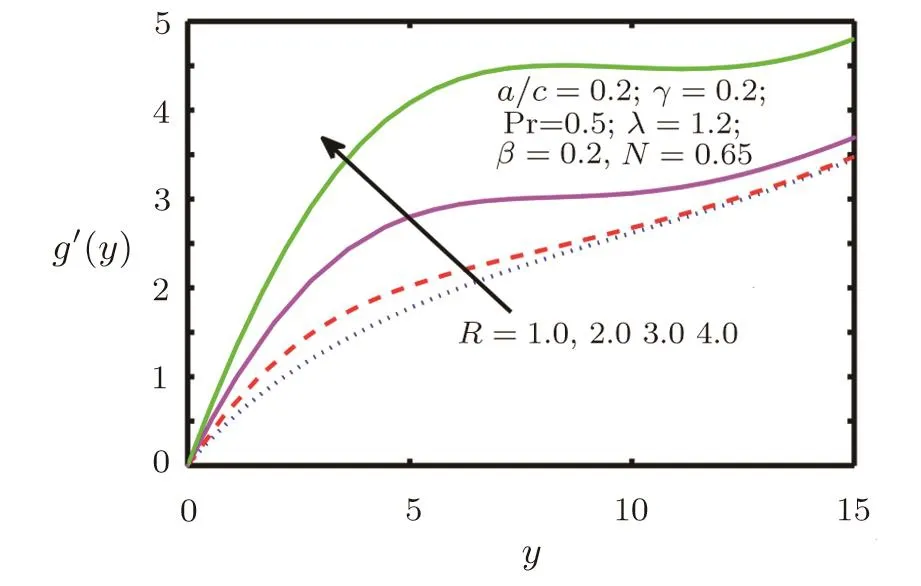
Fig.5 Velocity Pro file g′(y)for R.

Fig.6 Velocity Pro file g′(y)for Pr.
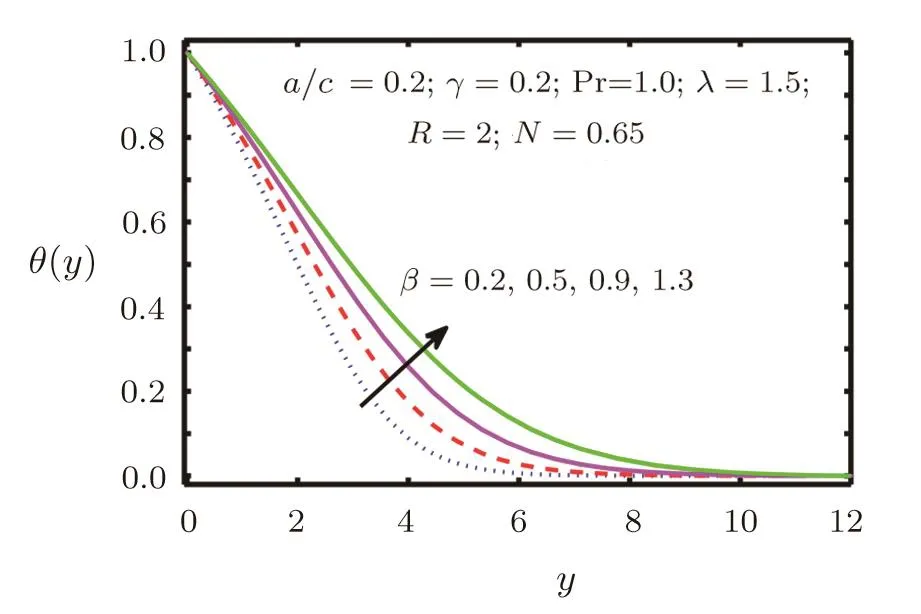
Fig.7 Temperature Pro file θ(y)for β.

Fig.8 Temperature Pro file θ(y)for R.

Fig.9 Temperature Pro file θ(y)for N.

Fig.10 Temperature Pro file θ(y)for Pr.
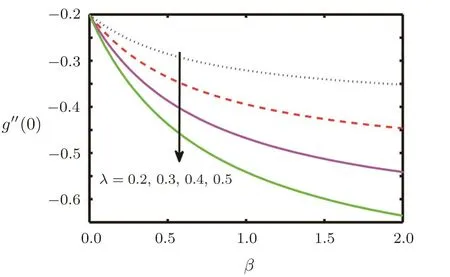
Fig.11 Behaviour of g′′(0)against β for λ.
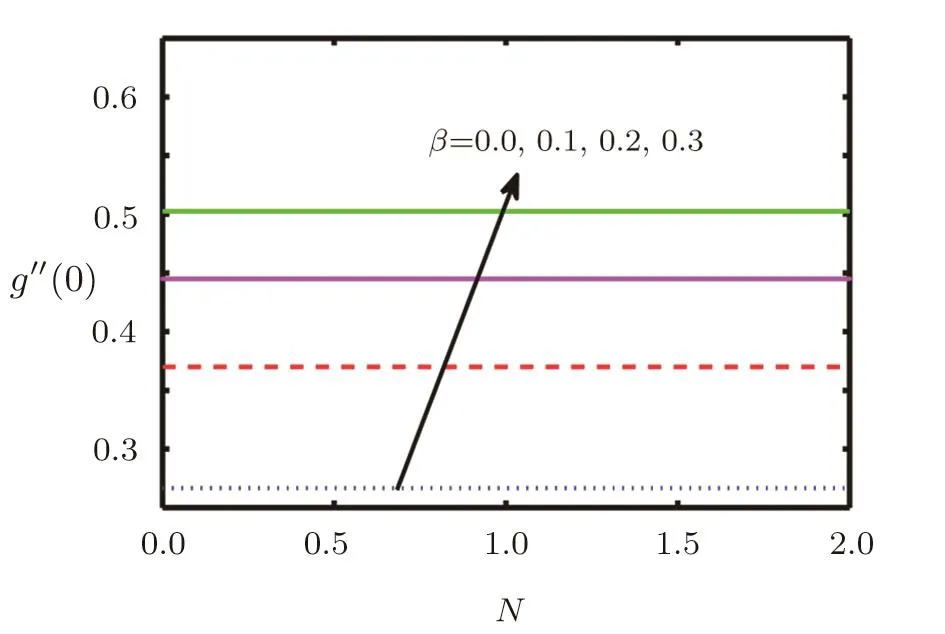
Fig.12 Behaviour of g′′(0)against N for β.
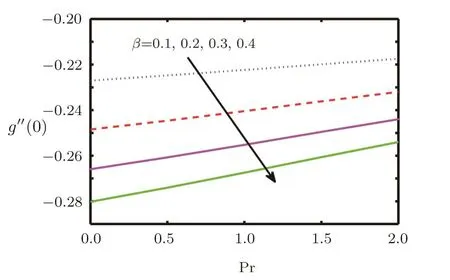
Fig.13 Behaviour of g′′(0)against Pr for β.
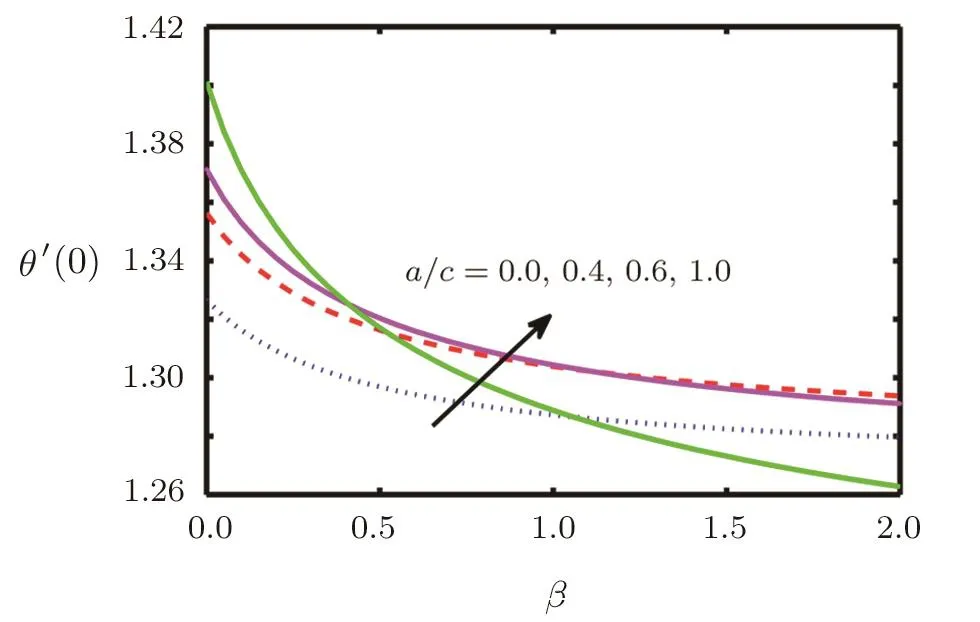
Fig.14 Behaviour of θ′(0)against β for a/c.
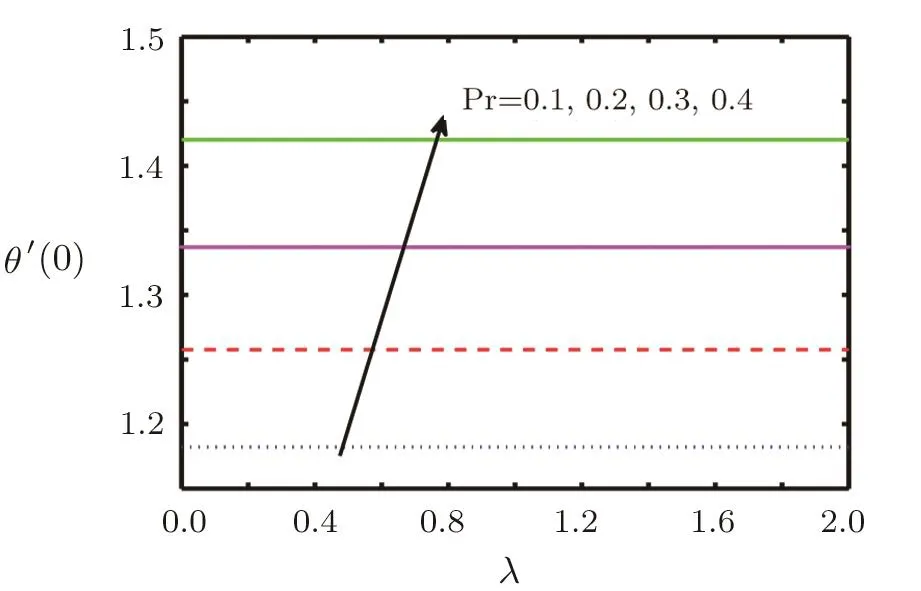
Fig.15 Behaviour of θ′(0)against λ for Pr.
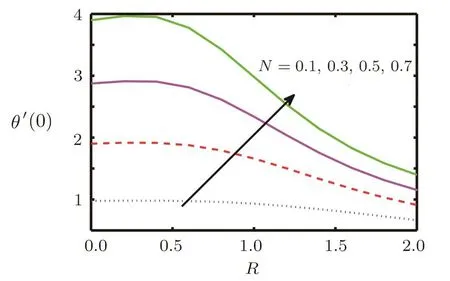
Fig.16 Behaviour of θ′(0)against R for N.

Fig.17 Behaviour of θ′(0)against Pr for R.
6 Conclusion
Natural convection on flow of a non-aligned Casson fluid has been investigated in the presence of non-linear thermal radiation.The core outcomes of this study are summarized as follows
• Normal velocity pro file f′(y)decreases for increase in Casson fluid parameter β.
• Tangential velocity pro file g′(y)enhances with mixed convection parameter λ,temperature ratio R and radiation parameter N,while it decreases with an increase in Prandtl number Pr.
•Momentum boundarylayerthicknessdecreases while thermal boundary layer thickness increases for Casson fluid parameter β,Also it rises for temperature ratio R and radiation parameter N.
• Tangential skin friction coefficient g′′(0)increases for Casson fluid parameter β against radiation parameter N and Prandtl number Pr.
[1]A.J.Chamkha,Int.Commun.Heat Mass Transf.25(1998)417.
[2]A.J.Chamkha and C.Issa,Int.Commun.Heat Mass Transf.26(1999)717.
[3]M.Kumari,Mech.Res.Commun.28(2001)339.
[4]A.Ishak,R.Nazar,and I.Pop,Meccanica 41(2006)509.
[5]O.Aydın and A.Kaya,Appl.Math.Modelling 31(2007)843.
[6]L.Y.Yian,N.Amin,and I.Pop,Int.J.Heat Mass Transf.50(2007)4855.
[7]S.Isa,N.Arifin,and R.Nazar,Malaysian Journal of Fundamental and Applied Sciences 10(2014)22.
[8]S.Nadeem,R.Mehmood,and N.S.Akbar,International Journal of Thermal Sciences 78(2014)90.
[9]S.Nadeem,R.Mehmood,and S.Motsa,International Journal of Thermal Sciences 92(2015)162.
[10]Y.Lok,N.Amin,and I.Pop,Int.J.Non-Linear Mech.41(2006)622.
[11]S.Nadeem,A.Hussain,and M.Khan,Communications in Nonlinear Science and Numerical Simulation 15(2010)475.
[12]R.A.Van Gorder,K.Vajravelu,and I.Pop,Meccanica 47(2012)31.
[13]S.Nadeem,et al.,Mathematical Problems in Engineering 2012(2012)1.
[14]S.Nadeem,R.Mehmood,and N.S.Akbar,Int.J.Heat Mass Transf.57(2013)679.
[15]M.Alam,M.A.Khatun,M.Asiya,M.Rahman,and K.Vajravelu,International Journal of Mechanical Sciences 105(2016)191.
[16]W.Khan,O.Makinde,and Z.Khan,International Journal of Heat and Mass Transfer 96(2016)525.
[17]R.Kumar and S.Sood,Int.J.Appl.Comput.Math.DOIq0.1007/540819-016-0150-2.
[18]M.Medikare,S.Joga,and K.K.Chidem,American Journal of Computational Mathematics 6(2016)37.
[19]S.Saleem,S.Nadeem,and M.Awais,Journal of Aerospace Engineering 29(2016)04016009.
[20]M.Samad and C.Podder,Bangladesh Journal of Scientific Research 27(2016)187.
[21]R.Seshadri and J.Sabaskar,International Journal for Computational Methods in Engineering Science and Mechanics 17(2016)127.
[22]P.D.Weidman and E.L.Perocco,Phys.Fluids(1994-present)28(2016)023603.
[23]S.Mukhopadhyay and K.Vajravelu,J.Hydro.Ser.B 25(2013)591.
[24]S.Nadeem,et al.,Alex.Eng.J.52(2013)577.
[25]S.Pramanik,Ain Shams Eng.J.5(2014)205.
[26]N.S.Akbar,Journal of Magnetism and Magnetic Materials 378(2015)463.
[27]K.Ramesh and M.Devakar,Ain Shams Eng.J.6(2015)967.
[28]K.Vajravelu and A.Hadjinicolaou,Int.Commun.Heat Mass Transf.20(1993)417.
[29]K.Bhattacharyya and K.Vajravelu,Communications in Nonlinear Science and Numerical Simulation 17(2012)2728.
[30]B.K.Jha,A.K.Samaila,and A.O.Ajibade,Afrika Matematika 26(2015)99.
[31]K.Vajravelu,K.Prasad,and C.O.Ng,Nonlinear Analysis:Real World Applications 14(2013)455.
[32]A.J.Chamkha,et al.,Meccanica 48(2013)275.
[33]S.Nadeem,R.Mehmood,and N.S.Akbar,Journal of Computational and Theoretical Nanoscience 12(2015)605.
[34]S.Nadeem,S.Zaheer,and T.Fang,Numerical Algorithms 57(2011)187.
[35]S.Mukhopadhyay,et al.,Meccanica 47(2012)153.
[36]N.Noor,S.Abbasbandy,and I.Hashim,International Journal of Heat and Mass Transfer 55(2012)2122.
[37]A.J.Chamkha,et al.,Transport in Porous Media 91(2012)261.
[38]M.Turkyilmazoglu and I.Pop,International Journal of Heat and Mass Transfer 59(2013)167.
[39]M.Sheikholeslami,et al.,Journal of Computational and Theoretical Nanoscience 11(2014)486.
[40]M.Sheikholeslami,et al.,Journal of Magnetism and Magnetic Materials 374(2015)36.
[41]T.V.Laxmi and B.Shankar,Journal of Applied Mathematics and Physics 4(2016)307.
[42]R.Ellahi,Commun.Theor.Phys.63(2015)353.
[43]R.Ellahi,et al.,Journal of Nanoengineering and Nanosystems 225(2011)123.
[44]R.Ellahi,M.Mubeshir Bhatti,C.Fetecau,and K.Vafai,Commun.Theor.Phys.65(2016)66.
杂志排行
Communications in Theoretical Physics的其它文章
- Pressure Oscillating Flow in Corrugated Parallel Channel∗
- Strong Decays of Charm Mesons (2680),(2760),(3000)∗
- The Role of a1(1260)in π−p →(1260)p and π−p → π−ρ0p Reactions Near Threshold∗
- Dilepton from Passage of Jets Through Spherical Expanding QGP∗
- Weibel Instability Growth Rate in Magnetized Plasmas with Quasi-Relativistic Distribution Function
- Quantum Private Comparison of Equality Based on Five-Particle Cluster State∗
