Multiply Kink and Anti-Kink Solutions for a Coupled Camassa–Holm Type Equation∗

Yuan-Li Li(李园丽)and Qi-Lao Zha(扎其劳)

College of Mathematics Science,Inner Mongolia Normal University,Huhhot 010022,China

1 Introduction

The Camassa–Holm(CH)equation

was rediscovered by Camassa and Holm in 1993,[1]by means of the asymptotic approximation of the Hamiltonian for the incompressible Euler equation,modeling the unidirectional propagation of shallow water waves over a flat bottom. Its various properties are established in a large number of literatures,such as the Lax pair representation,[1]bi-Hamiltonian structure,[1−2]infinitely conservation laws[2]and so on. Subsequently,using the inverse scattering transformation,[3]Darboux transformation[4]and so on,its peakon solutions can be constructed and they are orbitally stable.[5]It became remarkable because it possesses peakon wave solutions,[1,6]which have been of great research interest.The traveling wave solutions of the CH equation was analyzed in detail[7]and its dynamics of the interaction of peakons were studied.[8]Futhermore,the generalizations of CH equations and multi-component systems have been studied extensively.A two-component and a three-component CH systems introduced by Qu and Fu admits peakons and H1-norm conservation law.[9−10]We have studied the multi-peakon solutions for the two coupled CH equations explicitly.[11]The peakons are weak solutions,replicating a feature that waves jump finitely at its crest with discontinuous first order derivative and have the largest amplitude with corner at its crest.However,the kinks describe rising or descending from one asymptotic state to another.An integrable system with both quadratic and cubic nonlinearity has been studied as a generalization of the CH equation[12]

It possesses the weak kink and kink-peakon interacted solutions for the case of b 6=0.[12]The investigation of exact kink and multi-kink solutions for nonlinear equations play a vital role in nonlinear phenomena studying.Multi-kink solutions of mKdV(modified Korteweg-de Vries equation)are given,which is H1-stable and asymptotically stable,and the inelastic character of the kink-kink collision is shown in Ref.[13].Another prominent example is b-family equation,[14]

which is reduced to the celebrated CH equation with b=2.In the case of b=3,Eq.(3)is reduced to the Degasperis–Procesi equation.In Ref.[14],Xia and Qiao have studied its solutions and got its N-kink,bell-shape and hat-shape solitary solutions in the case of b=0 in an explicit formula.As one of the most prominent multi-component systems,the two-component Degasperis–Procesi(DP)equation,

where m=u − uxx,(k1,k2,k3)=(1,1,λ)or(λ,1,0)are studied by Yu and Tian.[15]Its breaking kink(or antikink)and solitary wave solutions have been investigated under different parameter conditions.[15]The peakons and weak kink solutions for another new integrable twocomponent CH system[16]are considered by Yan and his coworkers.Recently,Geng and Wang introduced a 4×4 matrix spectral problem and derived a coupled CH type equation with cubic nonlinearity[17−18]

Equation(5)has bi-Hamiltonian structures and is shown to be completely integrable with following Lax pairs[17−18]

where

and k1=(1/2λ2)+qxrx+qr,k2=(1/2)(qrx− qxr).Its in finite sequences of conservation laws and dynamical system of N-peakon solutions are also constructed by Geng and Wang.[17]In this paper,we can obtain the multi-kink solutions explicitly under the assumption that

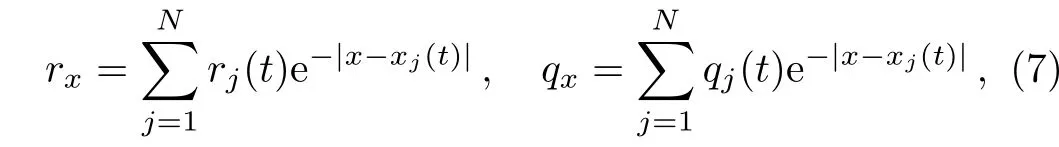
which have peakons form.Integrating in the weak sense,the multi-kinks have the following form

The main structure of this paper is as follows.In Secs.2 and 3,kink solutions,containing exponential function,are established in an explicit formula and plotted.And then,its various type kinks are also studied under different integrable constants conditions by figures.Some conclusions are drawn in Sec.4.Within our knowledge,the method in this paper may be a useful way to get multikinks for CH type equations,whose multi-kink solutions were rarely shown explicitly but single-kinks.

2 Multi-Kink Solutions of the Coupled CH Type System Eq.(5)

2.1 Single-Kink Solutions to Eq.(5)

For N=1,let us make the following ansatz of the single-kink solutions

where r1,q1,and x1are functions of t to be determined.

which implies solutions Eq.(9)are single-kink solutions with certain t.The second order and higher order partial derivatives of v,w do not exist at x=x1.Howerer,in the weak sense,their derivatives and v,w can be read as

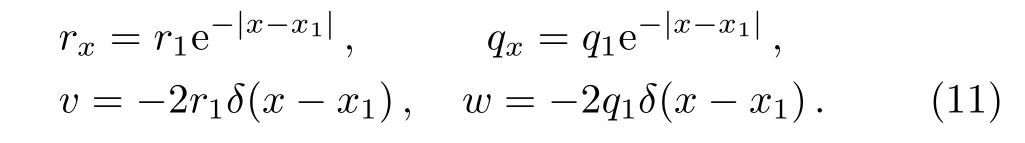
Substituting Eq.(11)into Eq.(5),a direct calculation gives that

where C is an integration constant.Thus the single-kink solutions(9)become

Because of the kink position x=C,the single-kink solution is stationary and its amplitude grow or decay exponentially with time t.The 3D graph of the obtained stationary kink solution Eq.(13)are shown in Fig.1 when C1,2>0.By choosing different constants Ci,i=1,2,Eq.(8)leads to different types.

Fig.1 3D graphs of the single-kink solutions for r and q defined by Eq.(13)with C=2,C1=1,C2=2.

2.2 Two-Kink or Antikink Solutions to Eq.(5)

In case of N=2,the equation also admits solutions

Moreover,we can obtain their derivatives in the weak sense as follows

Without loss of generality,we let x1−x2>0.Substituting Eq.(15)into Eq.(5)and integrating against the test functions,we can see the following dynamical equations

The above formula x1t−x2t=0 implies that the kinks will be never collide and the distance of the two positions does not change along with the time t.From the above equations,we arrive at the relations as follows

where C is a positive integrate constant.From the above equations,we may conclude

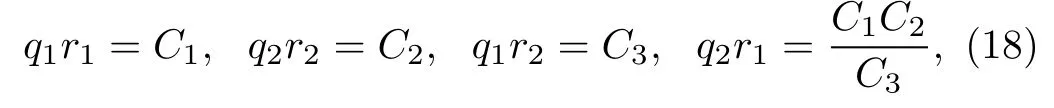
where Ci,i=1,2,3,are arbitrary constants.Thus,according to the dynamical system,the functions ri,xiand qi,(i=1,2)are calculated as

Obviously,the kink soliton solutions can be given explicitly

where

Case 1If Ci>0,i=1,2,3,according to Eq.(20),the solutions r,q are two-kink solutions or two-antikink solutions.When C4>0,with some special constants,we can plot the 2D and 3D graphs of two-kink solutions as shown in Figs.2 and 3.Moreover,two-antikink solutions can be obtained with C4<0 as shown in Figs.4 and 5.

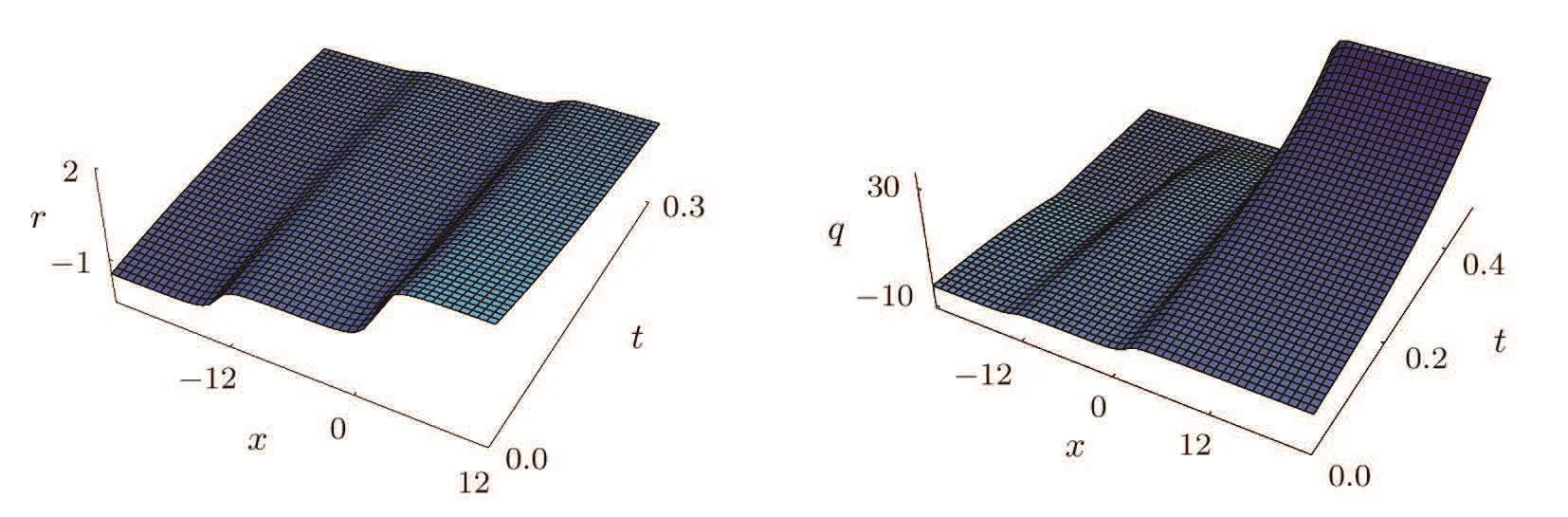
Fig.2 3D graphs of the two-kink solutions for r and q defined by Eq.(20)with C=15,C1=2,C2=1/2,C3=1,C4=1,C5=2.

Fig.3 2D graphs of the two-kink solutions defined by Eq.(20)with the above constants at time t=1/2 and 2/3.

Fig.4 3D graphs of the two anti-kink solutions for r and q defined by Eq.(20)with C=15,C1=1,C2=1/2,C3=2,C4=−1,C5=2.

Fig.5 2D graphs of the two anti-kink solutions for r and q defined by Eq.(20)with C=15,C1=2,C2=1/2,C3=1,C4=−1,C5=2 at time t=1/2 and 1/3.

Case 2When Ci<0,i=1,2,3,two-kink solutions r and two-antikink solutions q are obtained and plotted with C4>0 in Figs.6 and 7.In a similar way,the two-antikinks r and two-kinks q can be got readily with C4<0.

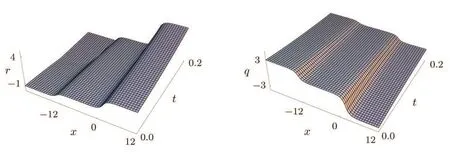
Fig.6 3D graphs of the two-kink and two anti-kink solutions for r and q defined by Eq.(20)with C=15,C1=−2,C2=−1/2,C3=−1,C4=1,C5=2.

Fig.7 3D graphs of the two-kink and two-antikink solutions for r and q defined by Eq.(20)with C=15,C1=−2,C2=−1/2,C3=−1,C4=1,C5=2 at time t=1/2 and 1/3.

Case 3Choosing C1,2>0,C3<0,its graphs of kink-antikink solutions determined by Eq.(20)can be drown out.In particular,if C1=C2=−C3,the solutions are reduced as

When C4<0,the solutions become kink-antikink solitons which are shown in Figs.8 and 9 with C=15,C1=2,C4=−1,C5=2 and their shapes look like hat-shape with a special t.Similarly,antikink-kink solutions also can be got with C4>0.

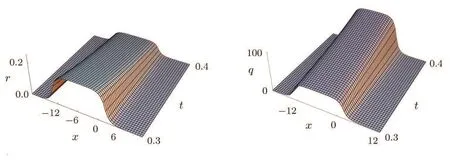
Fig.8 3D for the kink-antikink solutions r and q defined by Eq.(21)with C=15,C1=2,C4=−1,C5=2.

Fig.9 (a)and(b)are the kink-antikink solutions r and q defined by Eq.(21)with C=15,C1=2,C2=2,C3=−2,C4=−1,C5=2 at time t=1/2 and t=1/3.

Case 4If C1>0,C3>0,C2<0,r is a two-kink solution while q is an antikink-kink solution with C4>0 and r is a two-antikink solution while q is a kink-antikink solution with C4<0.Seeing Figs.10 and 11,the solutions are plotted with C4>0.Other type solutions are shown to have different shapes with special constants.

Fig.10 3D graphs for the two-kink solutions r and antikink-kink solutions q defined by Eq.(20)with C=15,C1=2,C2=−0.5,C3=1,C4=1,C4=2,C5=2.

Fig.11 (a)and(b)are 2D graphs for the two-kink solutions r and antikink-kink solutions q defined by Eq.(20)with above constants at time t=1/3 and t=2/3.

3 N-kink Solutions

With the help of the distribution theory,substituting Eq.(8)into Eq.(5),we get the dynamic system as follows

4 Conclusions

In this paper,we study the kink solutions for Eq.(5)explicitly.Moreover,we discuss some special solutions by choosing some different integrate constants by figures,such as two-kinks,two-antikinks,antikink-kink solutions and so on.Other kinds of kink solutions can be analyzed similarly.

[1]R.Camassa and D.D.Holm,Phys.Rev.Lett.71(1993)1661.

[2]B.Fuchssteiner and A.S.Fokas,Phys.D 4(1981/1982)47.

[3]A.Constantin and H.P.McKean,Commun.Pure Appl.Math.52(1999)949.

[4]Y.S.Li and J.Zhang,Proc.R.Soc.Lond.Ser.A 460(2004)2617.

[5]A.Constantin and W.A.Strauss,Commun.Pure Appl.Math.53(2000)603.

[6]J.P.Boyd,Appl.Math.Comput.81(1997)173.

[7]J.Lenells,J.Di ff.Equa.217(2005)393.

[8]A.Chertocka,J.G.Liu,and T.Pendletonc,Appl.Num.Math.93(2015)30.

[9]Y.Fu and C.Z.Qu,J.Math.Phys.50(2009)012906.

[10]C.Z.Qu and Y.Fu,Commun.Theor.Phys.53(2010)223.

[11]Y.L.Li and Q.L.Zha,Commun.Theor.Phys.65(2016)677.

[12]B.Q.Xia,Z.J.Qiao,and J.B.Li,arXiv:1205.2028v3[nlin.SI].

[13]Claudio M¯unoz,Disc.Cont.Dyn.Sys.36(2016)3811.

[14]B.Q.Xia and Z.J.Qiao,Phys.Lett.A 377(2013)2340.

[15]L.Q.Yu and L.X.Tian,Nonl.Anal.15(2014)140.

[16]K.Yan,Z.J.Qiao,and Z.Y.Yin,Commun.Math.Phys.336(2015)581.

[17]X.G.Geng and H.Wang,J.Math.Anal.Appl.403(2013)262.

[18]N.H.Li,J.S.Zhang,and L.H.Wu,Phys.Lett.A 380(2016)1508.