基于理想优基点法的原油储罐区布局多目标决策
2016-05-09张明广钱城江
李 阳,张明广,钱城江,桂 阳,冷 源
基于理想优基点法的原油储罐区布局多目标决策
李 阳1,张明广1,钱城江2,桂 阳1,冷 源1
(1.南京工业大学江苏省城市与工业安全重点实验室 江苏 南京 210009;
2.南京国泰协创安全科技有限公司,江苏 南京 211500)
原油罐区是重大的火灾爆炸危险源,储罐之间易产生多米诺效应加之危险源与居民区的距离较近,使罐区的风险较大。基于多目标决策理论对原油罐区的布局进行研究,首先分别计算出每种布局方案下土地使用面积、罐区内多米诺效应发生的综合失效概率、罐区对周边居民区的个人风险;然后运用多目标决策理论中的理想优基点法对各备选方案进行综合比较,选择最优的布局方案;最后通过对某居民区附近的原油罐区布局计算,从而验证该方法的可行性。
原油罐区布局;理想优基点法;多目标决策;多米诺效应;个人风险
原油罐区是原油储、运的重要场所,储罐数量多、储量大、生产设施多、工艺复杂,是火灾爆炸的危险源。国内消防部门对炼油厂的调查结果表明,在全部油罐火灾中,原油罐占40%,居油罐火灾事故的第一位[1]。台湾高雄大学[2]统计了1960—2003年间242起储罐事故,其中原油储罐事故66起,排名第一。原油储罐发生火灾事故的特点主要表现在火焰温度高、辐射热强,相邻储罐在强辐射热的影响下,液态油品产生相变,油罐内部因压力升高而导致油罐破损[3],很容易引发二次事故,导致事故多米诺效应,从而使得火势扩大,形成罐区火灾。
国内对原油罐区布局的设计主要依据各种指令性的规范,如《石油化工企业设计防火规范》(GB 50160—2008)、《石油化工企业厂区总平面布置》(SH/T 3053—2002)、《石油库设计规范》(GB 50074—2014)等。但随着原油罐区大型化,居民区不断向城市的郊区发展的趋势,标准规范中的安全距离已无法在有限的空间下,能够做到合理布局储存装置又不浪费一寸土地,且能确保装置间具有足够的安全距离、减少和消除多米诺效应、减弱罐区对周边人员密集区域的风险[4]。目前,国内虽然对原油罐区布局的研究较多[4-5],但主要集中于单目标优化方法的研究,如安全距离法、基于后果的方法、基于风险的方法和综合性的方法等,而对罐区布局的多目标优化方法的研究较少[6-8]。国外对原油罐区布局的设计主要依据Seveso Directive III,且主要是从风险、脆弱性的角度分析其合理性,忽略了储罐间的多米诺效应[9]。
罐区装置布局实质上是个多目标决策问题,如何在有限的土地资源下,通过罐区的不同布局方案决策,选择一个能使罐区内储罐间的多米诺效应、对周边设施的风险达到最小的布局方案,则是本文主要的研究内容。本文采用理想优基点法对原油罐区布局方案进行多目标决策研究。首先,根据有限个评价对象与理想化目标的接近程度进行排序,在现有的对象中进行相对优劣的评价;然后将原始数据进行同趋势和归一化处理,可从同一指标与最优指标的距离之比计算中体现出同一指标间的接近度,这在一定程度上反映了离散程度,排序结果充分利用了原始数据信息;最后运用各级标准和待评价对象与规范统一的正、负理想点的均方根距离来计算其对应贴近度,进而得出相应的评价结果[10]。该方法在有限的数据情况下,能够定量反映不同评价单元的优劣程度,且直观、可靠、操作性强。
1 原油罐区布局多目标决策体系构建
本文从土地使用面积、储罐综合失效概率以及对居民区的个人风险三个方面,运用理想优基点法选择原油罐区最优布局方案,图1为建立的原油储罐布局多目标决策体系,整个体系分成计算层、属性层、方案层和决策层。
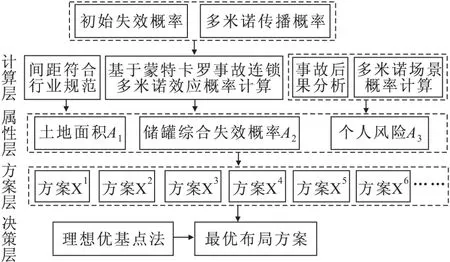
图1 原油罐区布局多目标决策体系Fig.1 System of the layout of a crude oil tank farm based on multi-objective decision making
2 实例应用与分析
本文以某居民区附近的原油罐区的布局设计为例,详细说明建立的原油罐区布局多目标决策体系的整个计算、决策过程。
2.1 原油罐区布局的基本情况
如图2所示,在距离居民区150 m处计划建造一个(座)原油库,常压储罐储存原油12 000 m3。本文的目标是在考虑土地资源、罐区内多米诺效应以及储罐对居民区的风险的情况下,通过多目标决策,得到最优的原油罐区布局。
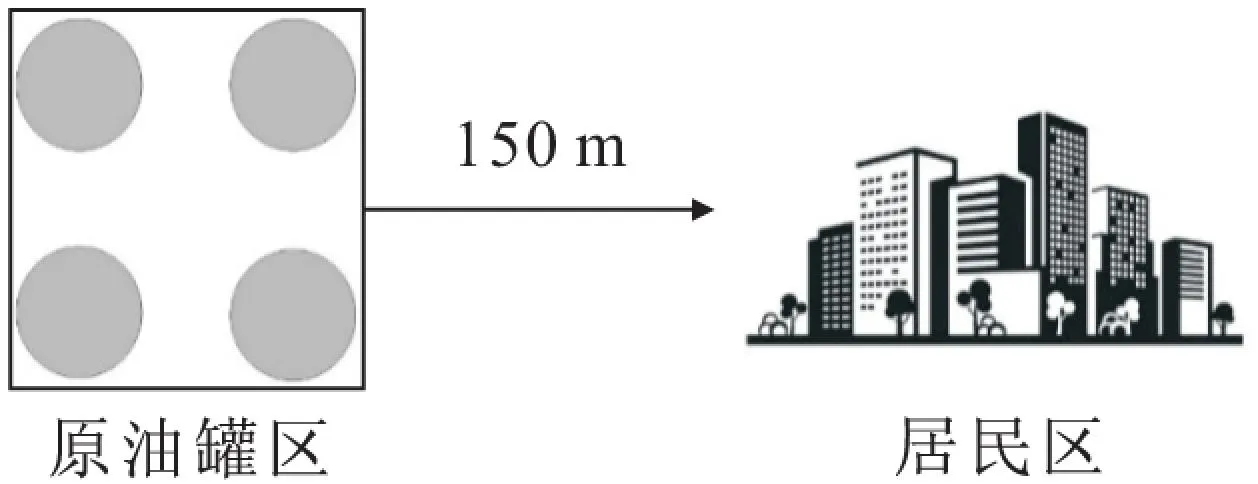
图2 某原油罐区Fig.2 Hypothetical crude oil tank farm
在满足相关规范[11-12]的前提下,本文设计了6种可能的原油储罐区布局方案,详见图3,各布局方案下的储罐参数见表1。
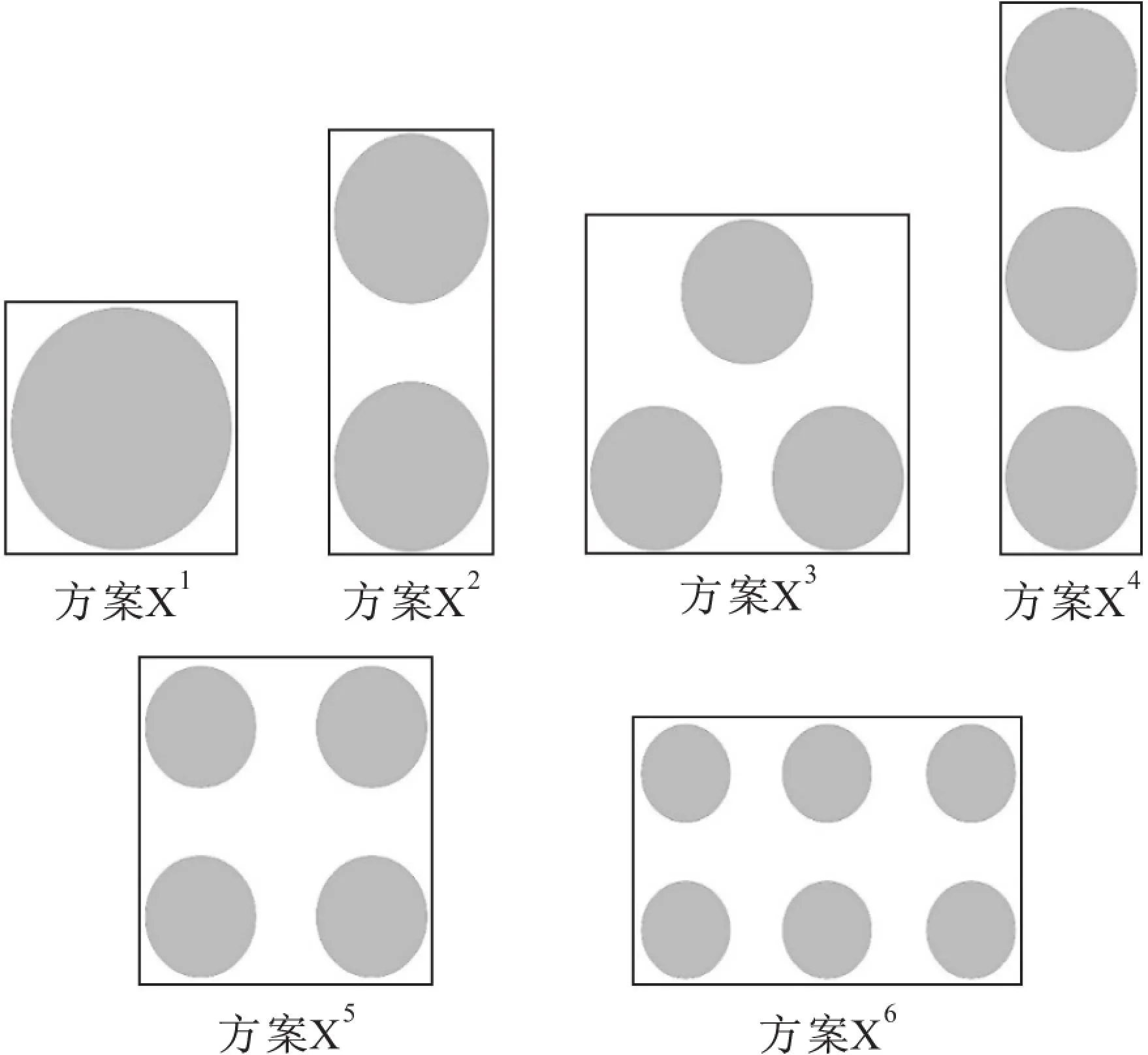
图3 原油储罐区的不同布局方案Fig.3 Alternatives for the layout of a crude oil tank farm
2.2 原油罐区多米诺综合失效概率计算
Abdolhamidzadeh等[13]运用蒙特卡罗法(Monte Carlo Method)开发出一种在理论分析的基础上计算装置多米诺效应概率的计算方法。本课题组在其研究成果的基础上,对其算法做了相应的改进,如在传播概率与随机数比较时增加一个装置间的内循环,以降低运算时间,并根据改进的算法开发出一款计算模拟软件,称之为“事故连锁多米诺效应概率计算方法”。该计算方法基于蒙特卡罗原理,运用多次试验来模拟实际的多装置系统发生事故连锁多米诺效应的情况,其最终的输出结果就是系统中每个装置的多米诺综合失效概率(装置自身失效概率以及在多米诺效应作用下的失效概率)。
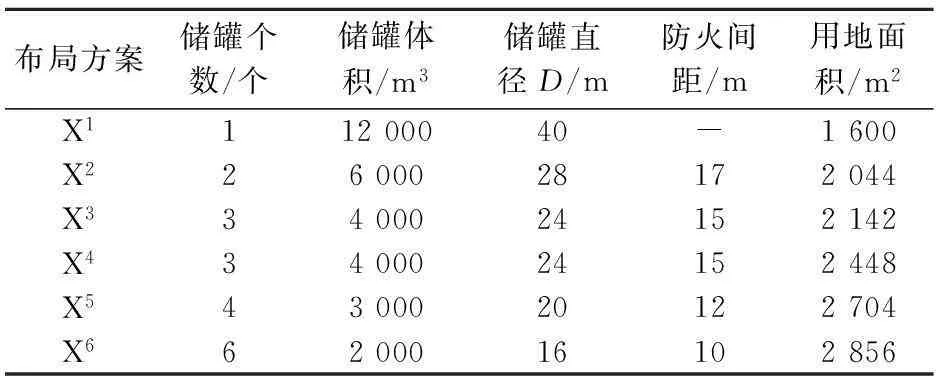
表1 不同原油罐区布局相关参数
原油储罐初始失效概率为5×10-6[14],对于储罐间的传播概率Pij的计算,Bagster等[15]提出储罐间传播概率与它们之间距离的平方呈反比的关系,即距离越远导致发生多米诺效应的概率越小,因此给出如下公式:
(1)
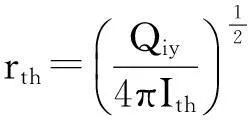
(2)
式中:rth为初级事故能引起破坏的最大距离,即达到多米诺效应破坏阈值的距离(m);rij为储罐之间的距离(m);Qiy为池火灾下储罐之间的热辐射通量(kW/m2);Ith为常压容器池火热辐射强度的破坏阈值(kW/m2),通常取15kW/m2[9]。
根据公式(2),可计算得到各布局方案储罐多米诺效应破坏阀值的距离rth,详见表2。
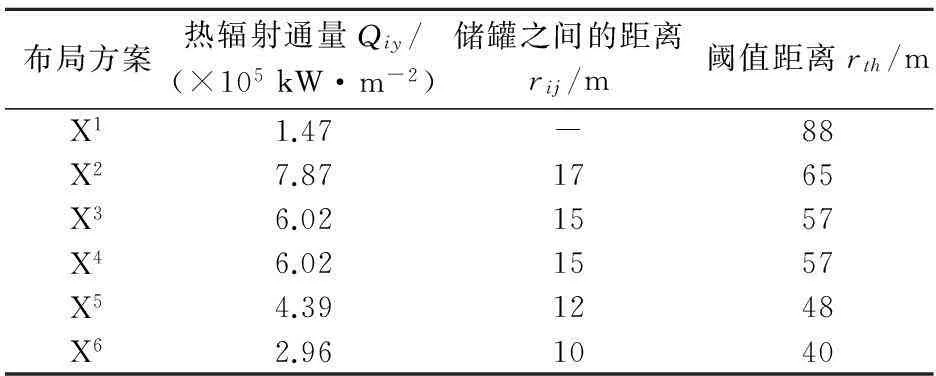
表2 各布局方案下储罐多米诺效应破坏阈值的距离
以布局方案X5为例,根据公式(1)分别计算出不同储罐间的传播概率Pij,并输入软件,最终计算得到布局X5的储罐多米诺综合失效概率,见图4。
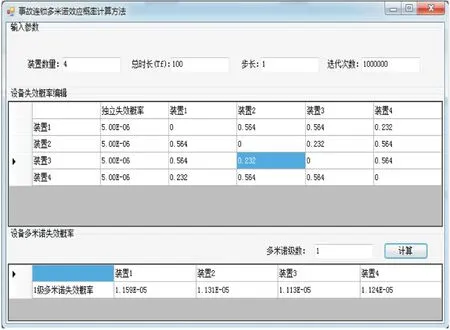
图4 布局方案X5的模拟结果Fig.4 Simulation results of the layout scheme X5
同理,可依次计算出每种布局方案下储罐的多米诺综合失效概率,详见表3。由表3可见,随着罐区内储罐数目的增加,在考虑储罐间的多米诺效应的情况下,储罐的多米诺综合失效概率变大。
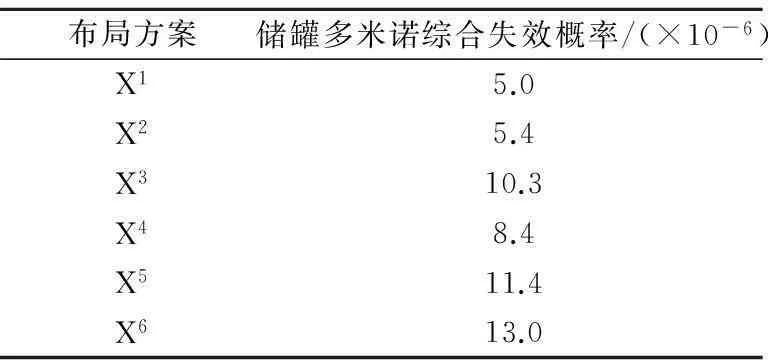
表3 不同布局方案下储罐的多米诺综合失效概率
2.3 原油罐区对居民区的个人风险计算
2.3.1 后果分析
脆弱性模型是一种被广泛认可且用于评价人体对有毒物质、热辐射或超压的剂量-反应关系的方法,该模型由标准正态概率分布函数的累积表达推导而来,其计算公式如下:
(其中,D为剂量,D=6×10-3I1.33t[16];μ和σ为高斯分布的中位数和方差);Y可通过下式计算:
Y=-14.9+2.56lnD
(4)
在考虑多个事故场景的情况下,总体的脆弱性Fd可以通过单个事故场景脆弱性组合进行计算。Cozzani等[17]提出的应用较为广泛的方法是假设整体脆弱性为多米诺事故中所有场景的死亡概率之和(上限为1):
(5)
式中:Fp为初始事故造成的人体脆弱性;Fd,i为多米诺事故场景i造成的人体脆弱性。
2.3.2 多米诺场景的事故概率
多米诺场景的事故概率的计算考虑同一初始事故引发的1个以上的2级事故。若不考虑2级事故的进一步升级,可认为升级事故是独立事件,则含k个发生2级事故的设备同时发生第m种多米诺场景的期望概率为[18]
(6)
(7)
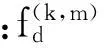
2.3.3 考虑多米诺效应的居民区个人风险
基于以上分析,在考虑多米诺效应的前提下居民区的个人风险R[18]可由下式计算:
(8)
2.3.4 不同布局方案下考虑多米诺效应的居民区个人风险值
通过以上计算方法,最终可计算得出各布局方案下考虑多米诺效应的居民区个人风险值,见表4。

表4 不同布局方案下考虑多米诺效应的居民区
2.4 多属性决策的理想优基点法
在对各布局方案进行决策时,主要考虑了罐区土地面积、罐区储罐综合失效概率以及居民区的个人风险值这三个属性,各属性的优劣状况最终都可以用定量的数值表示,因此在整个多属性决策过程中可以通过数值的计算得出最优解。
2.4.1 求方案的优基点
采用式X={X1,X2,X3,X4,X5,X6}的约束集表示6个可行的布局方案,根据不同布局方案各属性状况信息(见表5),将其转换为对所有属性状况都用定量表达的如下数值矩阵:

表5 不同布局方案各属性状况
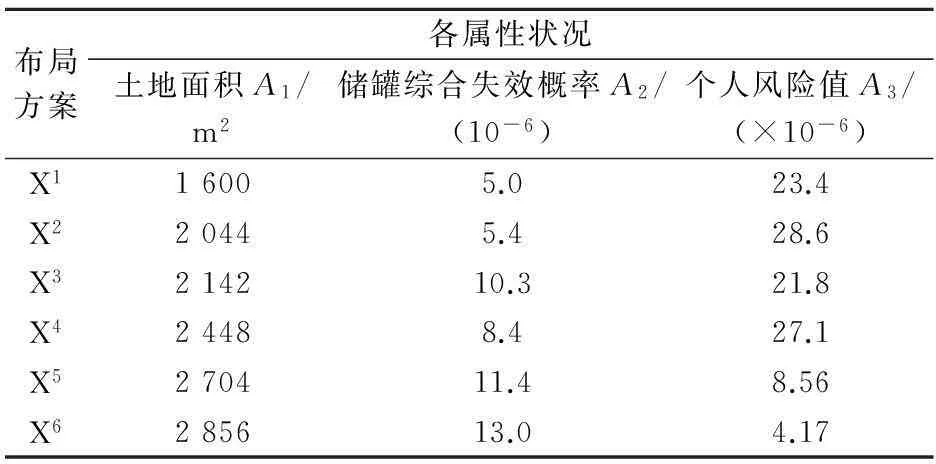
布局方案各属性状况土地面积A1/m2储罐综合失效概率A2/(10-6)个人风险值A3/(×10-6)X116005.023.4X220445.428.6X3214210.321.8X424488.427.1X5270411.48.56X6285613.04.17
因为属性A1、A2、A3这三对属性值都是要求达到最优极小化,而且都有不同的量纲单位,因此需要对矩阵中的值进行无量纲化处理,即
(9)

2.4.2 求理想优基点
由各优基点对应分量中的最大值组成的点,对于方案来说是最“理想”的点;相反地,由最小值组成的点,对于方案来说是最“不理想”的点,分别记[19]:
(10)
作m维属性空间Rm中的点,有
(11)
(12)
式中:zΔ为理想优基点;z为反理想优基点。
2.4.3 计算综合距离
优基点在三维空间上的反映就是一个点,找最优的方案,其实就是在某距离意义下寻找最接近理想优基点而最远离反理想优基点的点。如图5所示,在三维空间画出优基点z1,z2,z3,z4,z5,z6以及理想优基点zΔ和反理想优基点z。
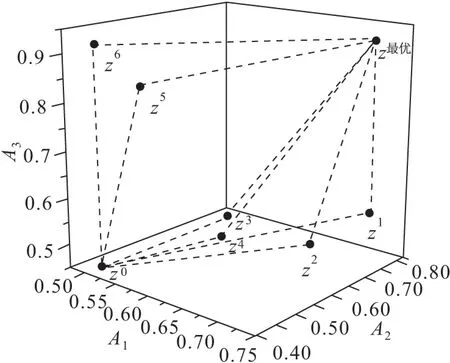
图5 各优基点在三维空间中的分布Fig.5 Distribution of each cardinal point in three- dimension space
各优基点与理想优基点和反理想优基点的距离计算公式如下:
(13)
以di作为衡量zi到zΔ和z的综合距离,其计算公式如下[19]:
(14)
根据公式(13)和(14),可计算得到不同布局方案下各优基点与理想优基点和反理想优基点的距离以及综合距离,见表6。
2.4.4 综合距离优选排序
根据距离最小原则,设xi,xj∈X(i≠j),若di 由表6的计算结果可得:d4>d3>d2>d1>d5>d6,根据距离最小原则,可知方案X6是最优偏好解。 表6 不同布局方案下、di的计算结果 虽然方案X6的储罐数量、储罐间的多米诺效应、土地使用面积是最多的,但罐区对周边的居民区的个人风险是最小的。由于理想优基点法是用空间距离大小来表征方案的优劣,出现最优结果是方案X6的情况,则是因为在计算时个人风险属性的极差相对于其他属性而言较大,所以导致风险所占的比重较大。 (1) 本文建立了原油罐区布局多目标决策体系,从罐区的土地面积、多米诺效应、对周边居民区的个人风险三个方面综合考虑原油罐区的布局,并以理想优基点法作为罐区布局方案选择的多目标决策方法,最终得到最优的布局方案。 (2) 理想优基点法是以靠近正理想解和远离负理想解两个基准作为评价依据来确定方案的排序,具有直观的几何意义。该方法基于数据样本本身,具有一定的客观性,且对原始数据的利用比较充分,信息损失比较少,适用于化工装置的多目标决策。但本文的研究还存在数据量有限、数据波动较大、没有典型的分布规律等缺陷,建议下一步可以通过扩充数据容量、对样本数据进行内在关联分析等方法来解决此问题。 [1] 许学瑞,帅健,吴宗之.大型原油库火灾定量风险评价[J].油气储运,2015(5):482-487. [2] Chang J I,Lin C C.A study of storage tank accidents[J].JournalofLossPreventionintheProcessIndustries,2006(19):51-59. [3] 苑静.石油储罐火灾爆炸危害控制的研究应用[D].天津:天津理工大学,2008. [4] 安君.多米诺效应风险评价在化工装置优化布局中的应用[D].沈阳:沈阳航空航天大学,2013. [5] 叶君乐,蒋军成,张明广,等.基于本质安全目标的化工厂装置平面布局优化[J].安全与环境学报,2011,11(1):167-171. [6] 米红梅,张悦,宋占兵.基于VEGA和DCGA的化工园区布局优化研究[J].中国安全生产科学技术,2013,9(5):45-51. [7] 张悦.基于风险分析的化工园区布局优化方法研究[D].北京:中国矿业大学(北京),2013. [8] 陈国华,施文松,赵远飞.基于风险的化工园区布局优化决策支持系统[J].中国安全科学学报,2012,22(7):141-146. [9] Khakzada N,Reniers G.Risk-based design of process plants with regard to domino effects and land use planning[J].JournalofHazardousMaterials,2015,299:289-297. [10]问国强.基于指标规范变换TOPSIS法的地表水环境质量评价[J].安全与环境工程,2015(3):65-69. [11]GB 50074—2014 石油库设计规范[S]. [12]GB 50160—2008 石油化工企业设计防火规范[S]. [13]Abdolhamidzadeh B,Abbasi T,Rashtchian D,et al.A new method for assessing domino effect in chemical process industry[J].JournalofHazardousMaterials,2010,182(1/2/3):416-426. [14]Cozzani V,Gubinelli G,Salzano E.Escalation thresholds in the assessment of domino accidental events[J].JournalofHazardousMaterials,2006,A129:1-21. [15]Bagster D F,Pitblado R M.The estimation of domino incident frequencies—An approach[J].ProcessSafetyEnvironmentalProtection,1991,69(4):195-199. [16]邢志祥,王云慧,杨扣华,等.化学流程工业多米诺效应风险评估的研究进展[J].中国安全科学学报,2014(10):144-150. [17]Cozzani V,Antonioni G,Spadom G.Quantitative assessment of domino scenarios by a GIS-based software tool[J].JournalofLossPreventionintheProcessIndustries,2006,19(5):463- 477. [18]马科伟.基于多米诺效应的区域定量风险评估方法研究[D].杭州:浙江工业大学,2010. [19]胡毓达.多目标决策:实用模型和选优方法[M].上海:上海科学技术出版社,2010. Multi-objective Decision Making for Layout of Crude Oil Tank Farms Based on the Method of Ideal Outranking Cardinal Point LI Yang1,ZHANG Mingguang1,QIAN Chengjiang2,GUI Yang1,LENG Yuan1 (1.JiangsuKeyLaboratoryofUrbanandIndustrialSafety,NanjingTechUniversity,Nanjing210009,China;2.NanjingGuoTaiXieChuangSafetyTechnologyCo.,Ltd,Nanjing211500,China) A crude oil tank farm is a major hazard source of fires and explosions.As domino effect tends to occur between storage tanks and hazard sources and the residential areas are close,the risk becomes relatively high.This paper conducts a research on the reasonable layout of crude oil tank farms based on the method of multi-objective decision making.First,the paper calculates the land use area,the comprehensive failure probabilities of domino effect in tank farms,and the individual risk of tank farms to the surrounding residential areas under each layout scheme respectively.Then,the paper applies the method of outranking cardinal point from the theory of multi-objective decision making to compare various alternatives,and selects the optimal layout scheme.Last,the paper calculates the layout of a crude oil tank farm near a residential area to testify the feasibility of the method.Key words:crude oil tank farm layout;method of ideal outranking cardinal point;multi-objective decision making;domino effect;individual risk 韦朝阳(1965-),男,研究员,主要从事重金属污染的生态与健康风险及环境修复等方面的研究。E-mail:weicy@igsnrr.ac.cn 1671-1556(2016)02-0066-05 2015-06-10 2016-01-06 江苏省自然科学基金面上项目(BK2012824) 李 阳(1991—),男,硕士研究生,主要研究方向为化工装置安全评价。E-mail:LY_njtech@126.com X928.03;TE88 A 10.13578/j.cnki.issn.1671-1556.2016.02.013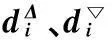
3 结论与建议
