有高温相变的电工钢热轧起浪的有限元分析
2016-05-09曹建国杨光辉周云松赖金权
曹建国,唐 慧,杨光辉,温 盾,周云松,赖金权
(1.北京科技大学机械工程学院,100083北京; 2.国家板带生产先进装备工程技术研究中心(北京科技大学),100083北京; 3.Jacobs School of Engineering,University of California-San Diego,CA 92093 La Jolla,San Diego,USA; 4.武汉钢铁(集团)公司,430083武汉)
有高温相变的电工钢热轧起浪的有限元分析
曹建国1,2,3,唐慧1,杨光辉1,温盾4,周云松4,赖金权4
(1.北京科技大学机械工程学院,100083北京; 2.国家板带生产先进装备工程技术研究中心(北京科技大学),100083北京; 3.Jacobs School of Engineering,University of California-San Diego,CA 92093 La Jolla,San Diego,USA; 4.武汉钢铁(集团)公司,430083武汉)
摘要:针对电工钢自由规程轧制过程起浪问题,开展电工钢不同冷却条件下的连续冷却相变转变温度分析测定和Gleeble热模拟实验,发现电工钢在975~875℃的奥氏体-铁素体两相区,随着轧制温度降低,变形抗力反而减小;电工钢大量同宽自由规程轧制下的工作辊出现严重的不均匀的箱型磨损和明显的热胀,综合辊形变化显著.考虑电工钢两相区变形抗力差异和综合辊形变化,建立电工钢热轧过程轧辊轧件的三维弹塑性耦合有限元模型,仿真分析轧制力、弯辊与窜辊对承载辊缝形状的影响,研究摩擦系数、压下量与轧制速度对带钢宽度方向内应力变化规律的影响,采用Shohet板形判据确定电工钢比例凸度残差变化路径,明确电工钢在“平坦死区”较大的上游机架出现“异常起浪”的生成过程.该方法为电工钢热轧板形的浪形控制提供了依据.
关键词:电工钢;热轧;热塑性变形;有限元建模;板形控制
目前,板形控制是制约电工钢大量同宽自由规程轧制(Schedule free rolling SFR)实现的主要瓶颈问题.电工钢甚至在具有较宽Shohet板形“平坦死区”[1-2]的热连轧精轧机组的上游机架出现严重的“异常”双边浪问题,影响了生产过程的稳定和产品质量.有限元是计算轧制问题最精确的数值计算方法之一[3-5].国内外学者和研究机构一般在构建热变形过程材料本构模型基础上,借助于有限元数值模拟技术实现轧制过程仿真.Calvillo等[6]通过压缩实验研究构建了无取向电工钢铁素体区本构方程;李长生课题组[7]利用热模拟实验研究了Fe-1.6%Si无取向电工钢热连轧粗轧区高温变形行为;董彦等[8]利用热模拟试验机研究了无取向电工钢相变问题,并基于Arrhenius型方程建立了单相区的本构关系模型; JIANG等[9〗[10]开展了板材轧制受力变形过程的有限元建模分析;徐新平等[11]通过刚塑性三维变形数值模拟软件分析得到实验轧机轧制Fe-3.2%Si硅钢不同厚度层应力及应变分布等.此外,国内外学者采用有限元数值模拟技术,对电工钢热轧SFR极端制造过程规模应用的CVC[12-13]、SmartCrown[14]、PC[15]、KWRS[16-17]和ASR[18]等大型主流轧机机型开展了不均匀变形的边降、凸度控制,以及不均匀磨损控制的数学模型与板形控制性能等研究.由于对电工钢高温热轧时相变规律及软化机制认识尚不完善,且不同研究者在制定电工钢热轧工艺上存在不同看法,目前,只得到电工钢薄板坯连铸连轧机组或宽带钢热连轧机粗轧的部分非优化本构关系模型,很少考虑电工钢高温热轧奥氏体-铁素体两相区变形抗力差异对板形建模、仿真和控制的影响,对电工钢热轧板形的浪形控制尤其是上游机架出现“异常起浪”不能合理解释且难以控制.
本文依托工业流程系统的热模拟获得电工钢高温相变规律和变形抗力特性,结合大型工业轧机显著磨损和热行为特性,建立弹塑性耦合有限元模型,开展电工钢SFR极端制造过程起浪的三维弹塑性有限元建模与仿真.
1 无取向电工钢热轧特性分析
1.1高温奥氏体-铁素体两相区轧制特性
进行热膨胀实验,采集热膨胀实验温度和膨胀量等数据,利用切线法获取电工钢在1、3、5、10、15 和20℃/s等不同冷却速度条件下奥氏体与铁素体相变的转变起始和终止温度,具体见表1.由表1可知,电工钢相变温度比其他一般钢种高,冷却速度的提升将使奥氏体转变为铁素体的温度降低,并且其相变区间为60~100℃.采用Gleeble热模拟试验在750~1 120℃,应变速率0.05~10.00 s-1条件下对电工钢进行了热模拟实验,分析得到不同变形速率下的温度-应力曲线(见图1).
由图1可知:电工钢存在明显的高温相变,其应力随温度的降低,经历了增大—减小—增大的变化趋势.热轧时在1 120~975℃为奥氏体单相区,在875~750℃为铁素体单相区,温度对变形抗力的影响符合一般金属变化规律,即温度降低应力随之增加;在975~875℃为奥氏体-铁素体两相区,由于奥氏体相强度较高,铁素体相强度较低,温度越低,奥氏体相向铁素体相转变越多,铁素体所占比例增大,应力随之降低,变形抗力反而减小.

图1 不同变形速率下的电工钢温度-应力关系曲线
采用THV红外热像仪现场实测得到了电工钢热连轧机各机架带钢表面温度分布,并采用轧制过程带钢温度场仿真模型的数值模拟方法[19-20],得到具体机架轧制过程带钢横截面温度分布.可知某热连轧机精轧F4机架出口带钢宽度方向中部区域(距离传动侧带钢边部35~1 245 mm)处于两相区,而边部区域(0~35 mm,1 245~1 280 mm)处于铁素体区.结合现场提取工程数据可知:某大型热连轧机粗轧R1和R2可逆机架的无取向电工钢轧制在奥氏体区进行;热连轧精轧机组F1~F3上游机架处在奥氏体-铁素体两相区; F4机架甚至出现带钢中部为两相区而边部为单相区; F5~F7下游机架处在铁素体区.

表1 试验用电工钢在不同冷却速度下的相变温度
1.2大量同宽自由规程轧制的辊形测试
由于电工钢热轧极端制造过程完整服役期内大量同宽的自由规程轧制特性,磨损量可达到普钢的2~3倍,严重、不均匀磨损问题非常突出,同时电工钢轧制热行为变化快,对板形影响大.对我国近年新建的世界上电工钢产量最大的某大型热连轧机进行了长期跟踪测试,以处于奥氏体-铁素体两相区轧制的热连轧机精轧F1~F4机架为例,轧辊下机时轧制量为875.74 t,产品轧制宽度为1 050~1 280 mm,其工作辊直径方向上、下机实测辊形如图2.由图2可知,电工钢轧制工作辊呈严重箱型磨损,尤其是F4机架表现得更为明显.电工钢大量同宽自由规程轧制的严重、不均匀磨损和明显的热胀影响承载辊缝形状,从而影响带钢内应力的分布规律.
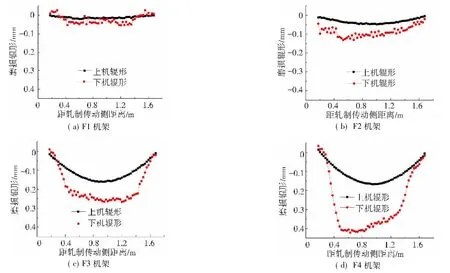
图2 电工钢热连轧精轧F1~F4机架工作辊上、下机实测辊形
2 电工钢轧制的三维弹塑性有限元变形耦合计算模型
为了兼顾模型的计算精度和效率[2],本文采取三维轧辊辊系弹性变形模型和轧件三维弹塑性变形模型耦合计算方式,即在辊系弹性变形模型中假设轧制力的分布,利用弹性变形模型计算出辊系弹性变形,为轧件三维弹塑性变形模型提供承载辊缝形状,在轧件三维弹塑性变形模型中假设轧辊为带承载辊缝形状的刚性体,然后利用两个模型计算结果,提取接触的轧制力和承载辊缝形状变形特征量作为联系模型间的桥梁,迭代求解达到模型间的平衡.
2.1三维弹塑性变形有限元耦合模型建立
辊系三维弹性变形模型可计算不同工作辊和支持辊辊形、弯辊力和窜辊策略下承载辊缝形状,建模具体假设如下: 1)忽略扭矩、润滑以及张力的影响; 2)轧辊均为匀质、各向同性材料,具有相同材质特性; 3)工作辊与支持辊之间无滑动.
现场跟踪观测可知,电工钢热连轧精轧机组F3~F5机架出现异常浪形,F4机架尤为严重,因此本文以F4机架为例建立模型.为了提高对现场工况模拟的精确性,将现场跟踪测试的电工钢精轧F4机架下机综合辊形添加到辊系弹性变形模型.考虑轧辊辊系的对称性,可建立1/4辊系模型(如图3),在剖面上施加对称约束,建模参数见表2.为提高辊缝的计算精度,选取等参单元Solid45(八节点六面体)作为主要单元,在与带钢的接触区域内采用高阶等参单元Solid95(二十节点六面体).辊系接触设置为柔-柔面接触问题,在可能发生接触的轧辊表面附加接触单元,支持辊表面定为目标面(TARGET170 ),工作辊表面定为接触面(CONTACT173).本模型考虑轧辊弹性变形,弹性模量取210 GPa,泊松比为0.3.结合轧件变形模型的辊系弹性变形模型可求得对应的承载辊缝形状.
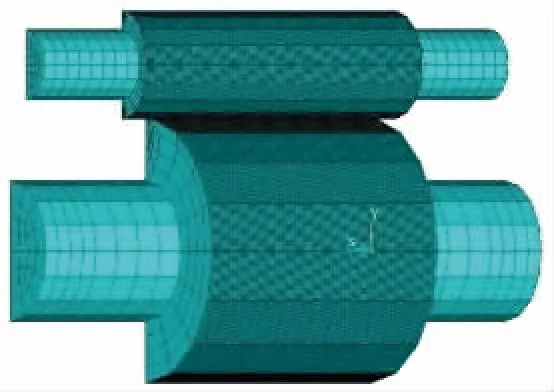
图3 辊系弹性变形有限元模型

表2 电工钢热轧精轧F4轧机辊系建模参数表mm
为了考虑电工钢奥氏体-铁素体两相区带来的变形抗力差异特性,轧件弹塑性变形有限元模型中将带钢分为一个中部区和两个边部区,边部区网格细化,并分别设置不同变形抗力值;且带钢与上、下工作辊的接触均为弹塑性.为了防止轧辊在轧制过程中上下波动,在带钢厚度方向中性层的4个轮廓节点上施加UX=0的约束.根据精轧F4机架实际轧制工况,高温带钢弹性模量和泊松比根据实际轧制温度灵活确定[20-21].取带钢入、出口厚度分别为7.5 mm和4.7 mm,宽度为1 280 mm,压下率为37.33%.仿真时初始速度设为1 m/s,接触后撤销带钢速度,改设轧辊转速10 rad/s,由张力和摩擦力来保持轧制进行,摩擦系数选0.3,张力设置为100 N/mm2.
本文通过轧制力的反算来验证所建耦合模型的假设与简化是否合理和准确.在辊系弹性变形模型中假设单位带宽轧制力为q=10 kN/mm,所得的承载辊缝形状经过叠加后加入轧件塑性变形模型进行计算,计算得到电工钢轧制变形阶段的轧制力平均值与施加值的误差为8.38%,具有较高计算精度,因此本文建立的三维辊件间接耦合模型可用于仿真计算.2.2仿真计算结果与影响因素分析
工业轧机F4机架轧制力为12.31~15.17 MN,弯辊力为300~1 200 kN,实际窜辊量为±100 mm,因此本文用单位轧制力10、12、14 kN/mm,弯辊力0、500、1 000 kN,窜辊行程-100、0、+100 mm进行模拟.辊系有限元模型确定的沿带钢宽度方向的承载辊缝形状随轧制力、弯辊力、窜辊行程的变化如图4所示,由图4可看出,考虑支持辊与工作辊之间的弹性压扁、支持辊挠曲、工作辊挠曲、工作辊实际辊形之后,所得的辊缝形状分布呈现倒“U”形,在辊缝中部区域变化平缓,在带钢边部容易因为压下量不均匀而导致可见浪形,非轧件宽度范围内影响不大.
由图4可知:单位轧制力分别为10、12、14 kN/mm时,辊缝凸度分别为47、52、61 μm,随着单位轧制力增加,承载辊缝凸度逐渐变大,说明轧制力在影响承载辊缝形状法向位移的同时还影响辊缝凸度的变化.弯辊力分别为0、500、1 000 kN时,辊缝凸度分别为47、17、2 μm,可见,随着弯辊力增加,承载辊缝凸度显著变小,说明弯辊力可显著减小辊缝凸度.弯辊力对辊缝的调节作用显著,且弯辊力连续可调使得弯辊力具有强大的板形控制性能,但弯辊力过大使承载辊缝形状向反向变化,易使宽带钢边部两侧形成局部突起.
考虑到电工钢热轧润滑轧制应用日益广泛,分别研究了不同摩擦系数、压下量和轧制速度对带内应力分布的影响规律,具体计算结果见表3.由表3可知,随着摩擦系数增加,带钢内应力分布大致呈线性增加:摩擦系数每增加0.1,带钢中部内应力增加10.41 MPa,带钢边部最大应力值增加21.07 MPa,相邻两节点间内应力差最大值增加3.85 MPa.随着压下量增大,带钢内应力分布大致呈线性增加,压下量每增加0.5 mm,带钢中部内应力平均值增加6.48 MPa,带钢边部应力最大值增加7.25 MPa,相邻两节点间内应力差最大值增加0.81 MPa.随着轧制速度增大,带钢内应力分布大致呈非线性增加,但数值上变化很小,主要是由于轧制速度越大,则带钢变形速率越大,导致轧件的变形抗力增大,需要更大的应力来使轧件发生变形;中部内应力从3.5 m/s到4.5 m/s增加了1.71 MPa,从4.5 m/s到5.5 m/s增加了9.93 MPa;其带钢边部最大应力值随着轧制速度的提高大致呈线性增加趋势,但变化很小,仅增加了1.33%,其带钢相邻节点内应力差最大值几乎不随轧制速度的变化而变化.
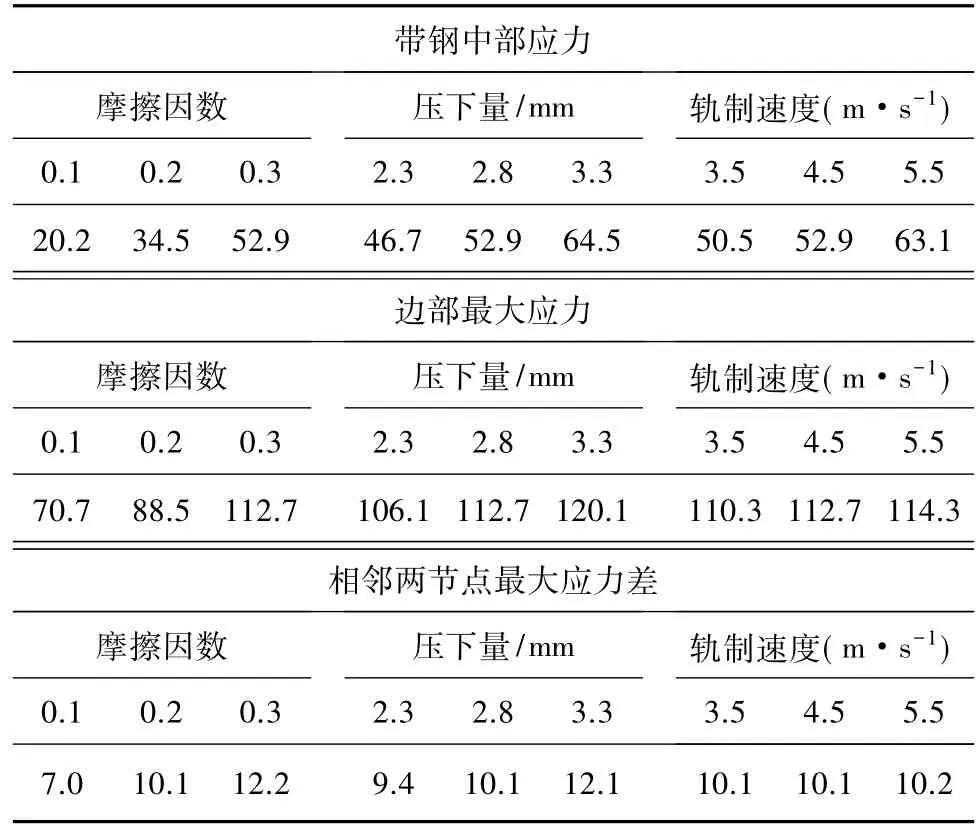
表3 不同摩擦系数、压下量和轧制速度变化对带钢内应力分布的影响 MPa
3 电工钢热轧过程起浪问题分析
采用建立的三维弹塑性变形有限元耦合模型,分别计算无取向电工钢F1~F3机架具有两相区轧制特性和F4机架带钢中部处于两相区边部单相区轧制特性的带钢宽度方向轧制力分布情况,结果见图10.由图10可知,无取向电工钢在F1~F3机架时带钢边部轧制力相对中部较小,而在F4机架处的带钢边部轧制力比带钢中部轧制力显著变大.
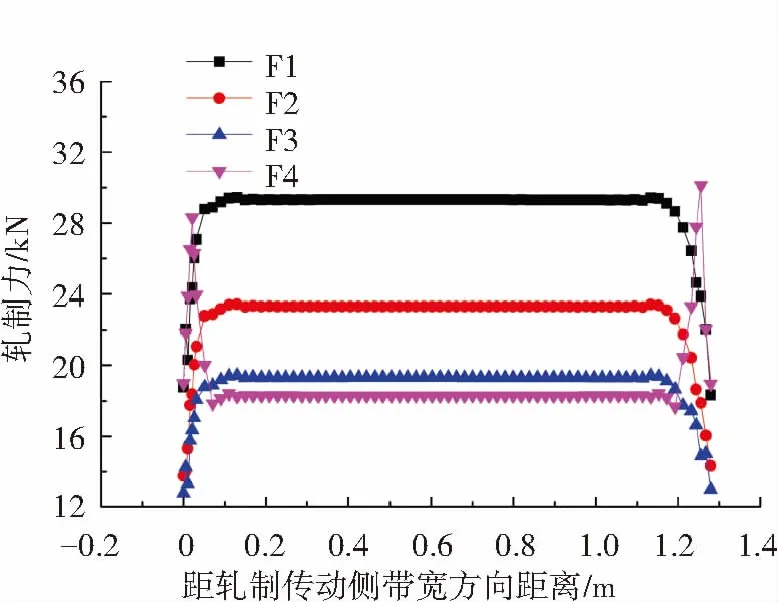
图5 热连轧机精轧F1-F4机架轧制力横向分布对比
电工钢热轧生产具有完整服役期内多机架连续轧制的特点,不仅仅要考虑辊缝对浪形的决定性,还要考虑机架之间的轧件变形,这种变形分为一次变形和二次变形两个阶段.轧件的一次变形是指带钢在机架中发生的变形,在此变形过程中,带钢的厚度由机架入口厚度H变为出口厚度h,可将不考虑来料凸度影响时计算出的负荷辊缝凸度定义为标准凸度N,以便于实际应用;其板凸度由入口凸度C变为出口凸度c,会产生比例凸度残差δ,若上一机架产生的纤维不均匀延伸没有完全消除掉,表现出来的平坦度为Ε,叠加后该机架出口时带钢板形平坦度的纤维相对延伸差为ε.轧件一次变形后的横截面形状与当时的工作辊负荷辊缝形状密切相关,在变形瞬间可以认为是一致的.一次变形后由于机架之间存在一定的距离,带钢游动于此段距离时,先前一次变形后由于各条纤维的延伸不均(纤维的相对延伸差为ε)便会导致内应力的产生.轧件的二次变形是指若一次变形后带钢纤维相对延伸差太大,经过蠕变后仍不能消除所有的纤维相对延伸差,当超过一定的界限后带钢将在外观上表现出浪形,即板形平坦度不为零.由于这种变形,带钢的横截面形状也将发生再次改变.在进入下一机架前,带钢的平坦度变为e,该机架带钢出口凸度c变为下一机架的入口凸度R.具体计算方法如下:


式中:η为本机架入口凸度系数,ω为辊缝宽展影响系数,α为平坦度系数,ε0为平坦度阈值,β为凸度系数.
根据现场工况实测数据,采用Shohet板形判据计算了2.3 mm×1 280 mm无取向电工钢宽幅薄板热连轧F1~F7机架的“平坦死区”和前述弹塑性有限元耦合模型与二次变形计算模型确定的比例凸度残差δ的变化路径,如图6所示.

图6 宽带钢热连轧机Shohet板形判据确定的比例凸度残差变化路径
由图6可知,随着电工钢在热连轧机上游机架F1~F3奥氏体-铁素体两相区轧制时带钢温度降低,轧制力随之减小,承载辊缝凸度变小,随后进入F4机架,带钢边部铁素体区和中部奥氏体-铁素体相区变形抗力出现的明显差异使带钢边部轧制压力大而中部轧制压力相对较小,且电工钢大量同宽的自由规程轧制使F4机架工作辊出现显著的磨损辊形和热辊形变化,均易导致带钢凸度明显变大,入口与出口比例凸度的残差显著变小,在F4机架时为-12.22,超过该机架“平坦死区”临界值.和常规薄板轧制相比,电工钢由于以上特性更易出现双边浪问题.一般认为各纤维条延伸不均匀导致的延伸差超过一定界限将出现可见浪形,而相邻两节点间内应力差则是导致各纤维条延伸差的主要因素.带钢边部和中部变形抗力出现明显差异,使带钢边部和中部之间内应力差相对较大,且进入F4机架以后,带钢凸度变大使边部相对压下变大也将导致相邻两节点间内应力差产生;而这两个内应力差都将直接导致纤维延伸差的产生,从而引发无取向电工钢热轧带钢产生边浪缺陷,甚至在带钢厚度较大的上游机架出现严重的双边浪,影响带钢成材率和生产效率.
强力液压弯辊系统和变凸度板形控制技术对辊缝凸度有很强连续可调的控制效果,可望控制上游机架两相区轧制进入F4机架后导致的带钢边部浪形过大问题.且随着摩擦系数和压下量的增加,相邻两节点间内应力差大致呈线性增加趋势;因此可通过改善轧制摩擦润滑条件、压下量设定,尤其是需要采用新的电工钢板形控制策略,应用强力液压弯辊系统和变凸度板形控制技术控制带钢比例凸度和带钢整体内应力的分布,从而控制浪形产生.
4 结 论
1)进行电工钢连续冷却相变转变温度分析测定和热模拟实验,发现电工钢存在明显的高温相变,且电工钢的应力随温度的降低,经历了增大—减小—增大的变化趋势.在奥氏体和铁素体单相区,温度降低,应力随之增加,符合一般金属变化规律;而在奥氏体-铁素体两相区,由于奥氏体相强度较高,铁素体相强度较低,温度越低,奥氏体相向铁素体相转变越多,铁素体相所占比例增大,变形抗力反而减小.
2)建立了电工钢热轧轧辊轧件的三维弹塑性变形的有限元数值模拟耦合模型,采用Shohet板形判据确定了电工钢热连轧自由规程轧制过程比例凸度残差变化路径,发现F4机架比例凸度残差变化大,显著超出“平坦死区”临界值,易出现明显的双边浪问题.
3)仿真发现,轧制过程中采用润滑轧制改善轧制摩擦状态和调整压下量设定,可改善和控制带钢整体内应力的分布.
4)电工钢上游机架“异常起浪”的主要原因是有高温相变的电工钢奥氏体-铁素体两相区变形抗力明显差异,以及大量同宽自由规程轧制的实际辊形出现严重箱型的显著综合辊形变化.可以通过采用新的电工钢板形控制策略、强力液压弯辊系统以及变凸度板形控制技术来增强轧机综合控制能力.
参考文献
[1]GINZBURG V B,AZZAM M.Selection of optimum strip profile and flatness technology for rolling mills[J].Iron and Steel Engineer,1997,74(7) : 30-38.
[2]曹建国,张杰,张少军.轧钢设备及自动控制[M].北京:化学工业出版社,2010: 161-173.
[3]MONTMITONNET P.Hot and cold strip rolling processes [J].Comput Meth Appl Mech Engrg,2006,195(48/ 49) : 6604-6625.
[4]李长生,熊尚武,RODRIGUES J,et al.金属塑性加工过程无网格数值模拟方法[M].沈阳:东北大学出版社,2004: 1-5.
[5]CHEN D C.An investigation into the shape rolling of sectioned sheets with internal voids using the finite element method[J].Procedia Engineering,2014,79(11) : 173-178.
[6]CALVILLO P R,BOULAAJAJ A,SINE M P,et al.On the hot working of FeSi ferritic steels[J].Materials Science and Engineering A,2014,606(11) : 127–138.
[7]李长生,韩斌,曹丽梅,等.Fe-1.6%Si无取向硅钢的热变形与相变规律[J].机械工程材料,2010,34(11) :95-98.
[8]董彦,龚志翔,肖国华.无取向电工钢的高温塑性变形流动应力[J].钢铁研究学报,2012,10: 53-58.
[9]JIANG Z Y,TIEU A K,LU C.EA FEM modelling of the elastic deformation zones in flat rolling[J].Journal of Materials Processing Technology,2004,146(2) : 167-174.
[10]胡长斌,童朝南,彭开香.热轧机有限元与神经网络集成建模[J].北京科技大学学报,2011,33(2) :221-226.
[11]徐新平,王均安.硅钢片轧制过程的有限元数值模拟[J].上海金属,2005,27(4) : 30-33.
[12]BERGER S,HOEN K,HOF H,et al.Evolution of CVC plus technology in hot rolling mills[J].Revue de Metallurgie,2008,105(1) : 44-49.
[13]XU G,LIU X J,ZHAO J R,et al.Analysis of CVC roll contour and determination of roll crown[J].Journal of University of Science and Technology Beijing,2007,14 (4) : 378-380.
[14]SEILINGER A,MAYRHOFER A,KAINZ A.SmartCrown—a new system for improved profile&flatness control in strip mills[J].Steel Times International,2002(11) : 11-13.
[15]徐利璞,周骏,彭艳.PC轧机轧制过程轧制力三维有限元模拟[J].燕山大学学报,2010,34(1) : 13-17.
[16]IKUO Y,MASANORI K,TOSHIKI H,et al.Transverse thickness profile control in hot and cold strip rolling by tapered-crown work roll shifting(K-WRS) mill[J].SEAISI Quarterly,1998,27(3) : 26-34.
[17]LI W G,LIU X H,GUO Z H,et al.Roll shifting strategy with varying stroke and step in hot strip mill[J].Journal of Central South University: Science&Technology(English Edition),2012,19(2) : 1226-1233.
[18]CAO J G,LIU S J,ZHANG J,et al.ASR work roll shifting strategy for schedule-free rolling in hot wide strip mills[J].Journal of Materials Processing Technology,2011,211 (11) : 1768-1775.
[19]TIAN L L,PAOLO P,ZHANG J,et al.Theoretical explanation of uneven transverse temperature distribution in wide thin strip rolling process[J].Journal of Iron and Steel Research International,2010,17(4) : 18-23.
[20]WANG X D,YANG Q,HE A R.Calculation of thermal stress affecting strip flatness change during run-out table cooling in hot steel strip rolling[J].Journal of Materials Processing Technology,2008,207(1/2/3) : 130-146.
[21]ZHOU Z Q,THOMSON P F,LAM Y C,et al.Numerical analysis of residual stress in hot-rolled steel strip on the run-out table[J].Journal of Materials Processing Technology,2003,132(1/2/3) : 184-197.
(编辑杨波)
Finite element analysis of edge wave for non-oriented electrical strip with high temperature phase transition
CAO Jianguo1,2,3,TANG Hui1,YANG Guanghui1,WEN Dun4,ZHOU Yunsong4,LAI Jinquan4
(1.School of Mechanical Engineering,University of Science and Technology Beijing,100083 Beijing,China; 2.National Engineering Research Center of Flat Rolling Equipment(University of Science and Technology Beijing),100083 Beijing,China; 3.Jacobs School of Engineering,University of California-San Diego,CA 92093 La Jolla,San Diego,USA; 4.Wuhan Iron&Steel (Group) Company,430083 Wuhan,China)
Abstract:For an edge wave problem of electrical steel in SFR (schedule-free rolling) process,the CCT curves and the Gleeble thermal stress-stain simulator are analyzed for electrical steel.The deformation resistance decreases as temperature is lowered in the austenite-ferrite region (975-875℃).The significant roll wear contours and thermal behaviors characteristics of SFR are obtained by the measured data of industrial mills.Considering the difference of deformation resistance with double phases and the actual roll contours,a 3D elastic-plastic finite element coupling model of roll stacks and strip is established for the effect of roll force,roll bending and shifting system on the loaded roll gap profile,and the influence of friction coefficient,strip thickness and rolling speed on strip internal stress distribution.The change path of ratio crown difference by Shohet criteria are attained to explain the formation process of irregular edge wave in upstream stands of hot rolling mills with larger flatness dead zones,which provides evidences for flatness control of electrical strip in hot rolling.
Keywords:electrical steel; hot rolling; thermoplastic deformation; finite element modeling; profile and flatness control
通信作者:曹建国,geocao@ ustb.edu.cn.
基金项目:高等学校博士学科专项科研基金(20120006110015).
作者简介:曹建国(1971—),男,教授,博士生导师.
收稿日期:2014-12-18.
doi:10.11918/j.issn.0367-6234.2016.01.022
中图分类号:TG335.11
文献标志码:A
文章编号:0367-6234(2016) 01-0146-06
