学生在“说数学”中感受奇偶“美”——《和与积的奇偶性》教学

张 婷

【教学内容】

苏教版五年级数学下册第50～51页。

【教学目标】

1.使学生经历探索利用规律解决复杂问题的结构化的教学过程，发现并理解和与积的奇偶性的规律。

2.使学生在探索规律的过程中，经历“举出例子——观察比较——寻找特点——归纳规律”的方法结构，积累探索规律的相关经验。

3.在学生经历探索规律的结构过程中，进一步培养学生合作交流的能力和学生的语言表达能力，激发学生探究数学规律的兴趣和信心，提升学生的学习能力，并能感受奇数、偶数的美。

【教学重点】

探究并发现和与积的奇偶性。

【教学难点】

理解和归纳规律。

【教学准备】

ppt、三种表格、计算器、每个学生准备一道已经算出结果的连加或连乘的算式。

【教学过程】

一、课前“叙旧”，符号记忆

师：同学们，知道我们今天学什么吗？奇偶性的奇偶是什么意思？什么是奇数？什么是偶数？

师：明白了课题，我们就开始今天新课的学习。

二、猜想引入，引发好奇

师：今天，我们一起来探索和与积的奇偶性。（揭示课题）

1.游戏——猜想：

学生拿出课前准备的非零自然数的连加或连乘算式，学生报算式，教师迅速判断结果是奇数还是偶数。

【设计意图：让学生在课的一开始迅速感知这节课的教学内容，并通过猜想游戏形式激发起学生的好奇心和好胜心，为接下来知识的学习打下良好的基础。】

2.导语：学了今天的知识后，你也可以做到！

三、借助经验，探索规律

（一）活动一：

1.抛出问题，激发思考。

师：我们先来研究和的奇偶性，有什么规律可寻呢？（板书：和的奇偶性）

思考一下，先从几个数的和开始研究比较好呢？

预设：生回答：2个数、3个数、……

师：就按刚才那位同学说的，我们先来研究两个数的和。（板书：两个数）

从最简单的开始想起，是一种非常重要的数学思想。

2.简单问题，初步感受。

出示表格一：

任意选两个不是0的自然数，求出它们的和，再看看和是奇数还是偶数。

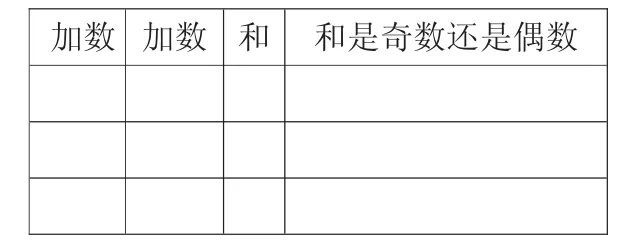
加数 加数 和 和是奇数还是偶数

活动要求：各自填表，再交流讨论，写下自己的发现。

3.深化认识，找出规律。

请学生带着自己的表格，上台说出发现了什么，其余同学给予评价与补充。

进一步验证：那你们写的算式也有这样的规律吗？我们来验证一下好吗？

谁愿意拿来给我们验证一下，放在展台上。

（1）这个算式符合哪个规律？这个算式呢？

（2）和是奇数，是什么样的加数？和是偶数，是什么样的加数？大家看看你们写的算式符合这个规律吗？自己验证一下。

师：符合吗？（符合）看来和是奇数还是偶数，与两个加数本身是奇数还是偶数有关系。

根据学生的发现，小结并板书：

偶数+偶数=偶数

奇数+奇数=偶数

奇数+偶数=奇数

【设计意图：让学生通过对已有经验的积累，自己动手操作，举例验证自己的发现，学生的主体地位更显突出，锻炼了学生的思维能力和合作能力。】

4.互动教学，及时巩固。

互动：我来说算式，你们来判断“和的奇偶性”好吗？

（课件：108+2340,123459+357,1325+2608）

师：打开我们的数学书，左右两边页码的和是奇数还是偶数？你知道这是为什么吗？

【设计意图：使学生明白，建构一种数学规律，必须通过不断探索，反复论证才能形成，这就是科学的态度。】

（二）活动二：

1.再抛问题，深度思考。

师：刚才研究了两个数的和，接下来继续研究多个数的和。（板书：多个数）

看看其中又蕴藏着怎样的规律呢？

2.点拨问题，交流验证。

出示表格二：

任意选几个不是0的自然数，写成连加算式，求出它们的和，再看看和是奇数还是偶数。

连加算式 和 和是奇数还是偶数加数中奇数的个数加数中偶数的个数

点拨：判断和的奇偶性关键要看什么？为什么？

加数中奇数的个数与和的奇偶性有什么样的关系？

活动要求：合作填表，再交流讨论，写下自己的发现。

3.汇报总结，归纳规律。

请学生带着自己的表格，再次说出多个数相加，发现了什么。

其余同学评价补充。

师：看看你们自己的例子，有没有不符合的？

根据学生的发现，总结并板书：

加数中奇数有奇数个，和是奇数；加数中奇数有偶数个，和是偶数。

4.解决问题，回顾反思。

（1）不计算判断下列加法算式的和是奇数还是偶数？

25+137

2+503+17+1235

36+289+5+73+86+6759+90

（2）1+3+5+……+29你是怎么想的？

小结：和的奇偶性和谁有关啊？面对这么复杂的问题，我们从简单的问题入手，找出规律来解决。在找规律时，可以先举出一些例子，再通过观察比较，找找有什么特点，从中发现规律。

（三）活动三：

师：接下来我们研究积的奇偶性。你打算先研究几个数的积？然后呢？

【设计意图：因有“和的奇偶性”的经验积累，“积的奇偶性”学生便会很快发现规律，应该让学生自然感知到思考问题的方法，活学活用。】

1.引发迁移，感受奇偶。

表格三：

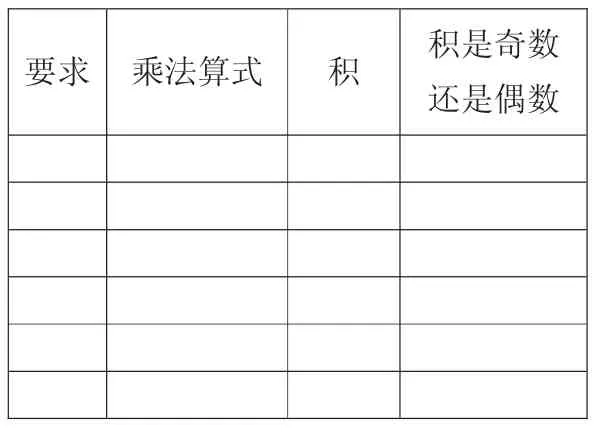
要求 乘法算式 积 积是奇数还是偶数

师：请你们根据刚才的经验，四人小组合作，举出例子，观察比较、寻找特点、找出规律。

2.说出想法，找出规律。

提问：哪个小组先来交流一下你们小组的结论？（学生交流）

小结并板书：

在乘法中，乘数都是奇数，积是奇数；乘数中只要有一个偶数，积就是偶数。

【设计意图：两个数→多个数。从简单的问题入手，层层递进，培养学生逻辑思维及演绎推理能力。这是重要的数学思想，也是学生解决问题的数学方法。】

四、反思质疑，归纳方法

师：本节课，我们一起学习了什么知识？刚才我们探索和发现了和与积的奇偶性的规律，回忆一下我们研究的过程，你学到了哪些解决问题的策略？

（适时板书：举例→验证→规律）

最后送大家一句名人名言：

把最复杂的变成最简单的，才是最高明的。——达·芬奇

【设计意图：这是一节“找规律”的数学活动课。学生在探索中不但要发现“和与积的奇偶性”的规律，更重要的是在发现规律的过程中感悟数学思考方法，而且还能感受到奇数、偶数独特的“美”。】