有效计算教学的策略思考——以《两位数乘两位数》教学为例

王陈亮

计算教学是小学数学教学的重要内容之一，它在教材中占有很大的比重。计算是小学生必须掌握的一项基本功，计算的好坏直接影响到学生对于其他数学知识的学习，如此看来能否扎实地搞好计算教学显得非常重要。但是现实的情况是，很多教师认为计算无非就是多做题。于是题海战术，就成了很多教师进行计算教学的法宝。长此以往，导致学生讨厌计算，甚至还渐渐地不喜欢数学了。

本文试图通过近几年对于计算教学的一些思考，结合“两位数乘两位数”一课的教学研究为例，来谈谈我的一些做法。希望给大家研究计算教学一些启示。

策略一：《导学单》，把准学生的真实起点

我区近几年一直在做课堂教学变革试验，力求通过变革转变我们的课堂教学。《导学单》的运用，就是教学方式变革亮点之一。其实，在以前的教学中，我们也偶尔会运用一下教学前测，了解一下学生的知识基础。但是相比于一般的教学前测，《导学单》更加关注学生的自主学习，能更好地展现学生的思维过程。这样对于我们准确把握学生的真实起点，客观分析学生的学习障碍，很有帮助。

在“两位数乘两位数”一课的教学中，哪些学生能利用已有的知识进行计算？哪些学生能正确笔算？哪些学生存在困难，无从下手。在课前，我针对本课的教学内容设计了《导学单》（如图），并且在课前让学生独立完成，并及时收集分析。

你好！非常感谢你的积级参与！老师相信，通过你的努力，一定会有所收获！导学单班级： 姓名：

喜羊羊玩具每个要14元，买了12个，一共要付多少钱？

1.把你的方法试着在下面的点子图上表示出来，想一想，该如何列式计算？

2.再想一想，还有不同的方法吗？

教材创设的是购书的情境，让学生计算一共有多少本书？考虑到三年级学生的年龄特征，再结合学生喜欢看动画片的特点，于是我创设了购买喜羊羊玩具这一情境，让学生计算“喜羊羊玩具每个要14元，买了12个，一共要付多少钱？”为了帮助学生思考，我提供了点子图，学生可以画一画，圈一圈帮助思考。为了充分展现学生的各种不同方法，我还设计了“再想一想，还有不同的方法吗”的问题。

课前，我对本校三年级3个班88位学生做了前测，给每位学生20分钟左右的时间进行计算，结果统计如下：

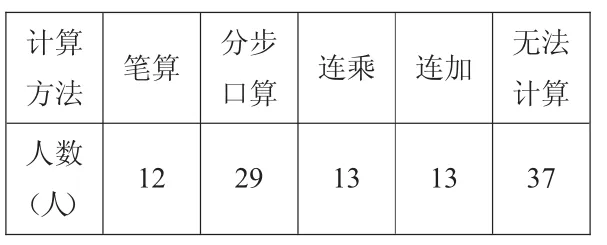
表1

表2

从统计结果可以看出：表1中有接近一半的学生面对“两位数乘两位数”的计算题不会计算。会计算的同学中，大部分的学生是用分步口算的方法，也有近七分之一的同学用笔算，也有几位学生能运用多种方法进行计算。

从表2中可以看出运用笔算的学生中能正确笔算的有8人，占总人数的十分之一，通过访谈情况几乎如出一辙，都是父母亲在课前教的，当追问竖式中每一步分别表示什么时，只有3位学生表达完全正确。

从《导学单》中可以看出，学生对于两位数乘两位数的计算起点是比较低的，大部分学生不能正确笔算，有些能笔算的也只是依样画葫芦，“知其然，不知其所以然”。但是可喜的是有近三分之一的学生会分步口算，其实口算和笔算是相通的，只要抓住之间的内在联系，就可以迁移过来。有了学情的准确把握，对于后续教学的安排就能够做到有的放矢了。

策略二：点子图，突破学生的算理理解

理解算理，掌握算法是计算教学的重中之重，必须让学生切实掌握，其中算理的理解是教学的关键。很多教师在教学中淡化算理的理解，教学的大部分时间都是让学生反复操练，题海战术。我觉得计算的熟练与否，必要的练习必不可少。但是我们不提倡盲目地练，机械的训练，而应该在学生理解的基础上进行适度的练习效果会更好。那么，如何更好地帮助学生理解计算的算理呢？“点子图”正好可以解决这一问题，利用点子图可以将直观与抽象紧密结合起来，借助直观的点子图帮助学生理解抽象的算理。

“两位数乘两位数”一课的笔算，对于初学者而言，是比较难的。因为学生之前学习的是多位数乘一位数，从一位数变成两位数，计算的步骤多了，也变得更加繁杂了，很多学生就不明白竖式为什么要写的这么麻烦，步骤这么多，积怎样定位等。这些都是学生理解的障碍所在，于是在教学中通过点子图帮助学生明白算理。如何利用点子图帮助学生理解算理呢？我做了如下的设计。

1．《导学单》中渗透点子图。

在《导学单》中，我除了提供需要解决的问题之外，还提供了点子图作为脚手架（如下图），当学生面对问题无从下手时，可以通过圈一圈、画一画，为学生的计算提供帮助。这是点子图运用的第一层次，但从实际的反馈来看，有些学生从点子图上得到了计算的方法，也有些学生没有将点子图很好地运用起来。

喜羊羊玩具每个要14元，买了12个，一共要付多少钱？

（1）把你的方法试着在下面的点子图上表示出来。想一想，该如何列式计算？

2．交流展示中运用点子图。

在交流展示计算方法时，如何让学生更清楚地表示自己的算法，同时也能让同伴明白自己的算法，这时候结合点子图的演示来帮助学生理解算理，使算理的理解变得更加直观。

在交流分步口算的方法时（如图），通过课件的同步展示，使每一步口算与点子图进行紧密的结合，帮助学生理解每一道算式的含义。

对于连乘的算法（如图），很多学生是比较难以理解的，此时如果通过点子图的演示，就变得非常简单，特别是个别聪明的学生，还能想到其他的方法：比如 14×3×4，12×2×7等等。因此，教学中通过电子图的适时演示，不仅能帮助学生理解算法，还能拓展学生的数学思维。

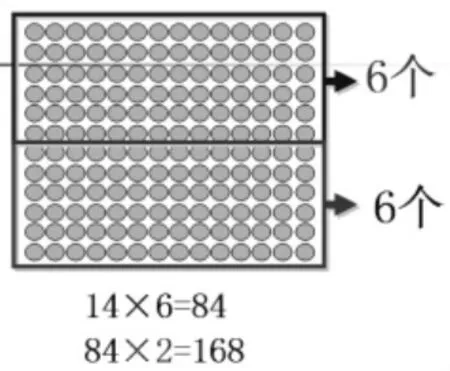
3．笔算中运用点子图。

两位数乘两位数的笔算，如果孤立地去看每一步的计算，那是相当繁琐的，步骤也很多。通过分析发现笔算的算法和分步口算的算法是一脉相承的，笔算无非是把几道口算综合到一道竖式里面。教学中，如果能让学生体会到这一点，那学生对于笔算的计算就不感到麻烦了。因此将笔算的算理与口算的方法进行有效沟通，让学生通过口算去理解笔算，接着再沟通点子图、口算和竖式三者之间的关系，从而帮助学生理解笔算的算理，从而掌握算法（如图）。

算理对于三年级的学生而言是抽象的，难以理解的，同时也是很多教师觉得计算难教的地方，似乎怎么讲都讲不清楚。但是如果在教学中适时地运用点子图来帮助理解算理，将大大降低学生理解的难度。点子图对于学生来说是直观的，借助点子图这一直观的教学材料帮助学生理解抽象的算理，能使学生更好地掌握两位数乘两位数的笔算方法。

策略三：错例分析，解决学生的疑难困惑

计算课的最终目的是使学生扎实掌握计算方法，形成计算技能，并为解决问题打下基础。教学中，学生计算方法掌握得如何？哪些地方容易出错？可以通过练习反馈学生的错误算法，在辨析交流中，弄清错误的根源在哪里？如何使计算能真正解决学生的疑难？错例分析是非常好的反馈交流形式。这里的疑难困惑可以从两个方面去分析：一是计算本身难点，这是学生面对新知时产生的困难；二是学生的现实难点，这是学生的真正困难所在。我们的错例就是及时反馈学生的问题所在，为解决学生的疑难而教。

在“两位数乘两位数”的教学中，我安排两次错例辨析：一次是在《导学单》的前测中，已经有8个学生利用笔算的方法进行计算，但是其中有4个学生的计算是错误的，通过分析发现，这些错误是比较典型的错误。在学生完成巩固练习之后，及时反馈学生在计算过程中出现的错误，引导学生进行交流，及时解决学生的问题。

1．前测中的错例分析。

从错例1中可以看出这种错误是学生在笔算中非常典型的错误，学生不明白4为什么要和十位上的数对齐，结果之所以正确，是因为他用口算的方法求出来的。因此，在交流中，重点就放在第二个积的书写位置上，让学生明白道理。

错例2中也是学生在计算中比较容易出现的错误，因为前面两步的计算都是用乘法，而到了第三步时，却要用加法计算，学生一不小心就错了。通过错例分析让学生明白计算需更细致、用心。

2．练习中错例分析。

在练习巩固环节中，学生独立完成以下3道题：

请列坚式计算：

学生练习时，我巡视了解学生中出现的错误，并进行展示辨析，让学生说说错在哪里？怎么订正？计算时我们要注意什么？

在错例辨析中，这些错误都是来源于学生自己，学生会觉得这样的错误是非常真实的，也非常熟悉，使学生感受到这是在真正解决自己的问题，学生会非常主动地投入到学习中。

策略四：渗透学法，引领学生自主学习

数学的思想方法很多，比如极限的思想、化归思想、符号化思想、转化思想……需要我们结合具体的教学内容进行合理渗透。

“两位数乘两位数”一课的教学中，我们应该渗透转化法。转化是数学教学中非常重要的数学思想方法。在本课的教学中，除了让学生理解笔算的算理，掌握计算的方法之外，学法的指导也是教学的一个隐性目标。我想数学中很多的数学知识，一旦学生掌握了方法，学生完全可以凭借自身已有的知识进行解决，就如本课的分步口算，连加计算，连乘计算等，学生可以将本课的新知转化成前面所学的知识进行计算。通过调查发现差不多有60%的同学能够利用旧知进行计算。同样，当学生今后面对一些新的问题时，也可以利用同样的方法去解决。教学中，对于“转化”思想方法的渗透，我是通过以下几个途径进行渗透的。

1．在新课教学前。

当学生根据情境列出算式14×12后，教师问：这道题与我们以前学过的计算有什么不一样？从而揭示：这是今天我们要研究的新知识“两位数乘两位数”。紧接着追问：你们能利用之前所学的知识去计算吗？让学生想办法利用所学的知识去计算,进行转化思想方法的初步渗透。

2．在整理环节中。

通过提问：请大家静静地回忆一下，本课的数学知识是怎么学会的？接着让学生回顾交流本节课的学习过程和方法，学生也能提到“转化”的方法。此时，再结合以下课件的分步演示，进一步梳理学法，提升学生的数学思想方法。

使学生明白“转化”的数学思想方法是非常重要的一种思想方法，我们今天这节课已用到，今后很多的数学学习中都会用到，当我们面对一个新问题时，我们可以想一想是不是可以利用已有的知识去解决。