基于遗传算法的人工神经网络预测多硝基化合物撞击感度

钱博文， 陈利平， 陈网桦

(南京理工大学化工学院， 江苏 南京 210094)

1 引 言

撞击感度是衡量含能材料安全性能的一个重要参数[1]，多硝基化合物在民用生产和军事上应用广泛，因此获得多硝基化合物的撞击感度数据具有一定实用价值。由于实验测试费时费力，且测试结果易受环境、操作人员、设备等因素的影响，此外，对于正处于探索阶段尚未合成出的物质而言，也无法通过实验获得测试值，因此有必要对理论预测撞击感度的方法进行研究。定量结构-性质相关性研究(Quantitative Structure Property Relationship，QSPR)是一种能根据分子结构实现有机物理化性质预测的有效方法，已广泛应用于有机物的各类理化性质及生物活性的预测中[2]。

近年来，国内外学者已经对撞击感度与其分子结构间的相关关系进行了广泛的探讨。赵俊[3]等人对36种硝基化合物和33种硝胺化合物的撞击感度和其分子特征量之间的关联顺序进行了研究。王睿[4-5]等人应用电性拓扑状态指数对41种多硝基苯类化合物和46种多硝基脂肪族化合物分别进行了撞击感度的定量构效关系研究。葛素红[6]等人计算并分析了18 种三硝基芳香族炸药分子的原子化能以及原子化能与分子的电子结构能的比值与撞击感度的关联关系。Guillaume Fayet[7]等人用最佳多元线性回归(B-MLR)研究60个硝胺类化合物的撞击感度与Codessa计算所得64个分子描述符间的线性关系。N. R. Badders[8]等人研究了22个多硝基化合物的撞击感度与6个量子化学参数间的相关性。这些研究只专注于特定种类的样本集，所用样本较少，所得模型的适用范围有很大的局限性。因此，也有学者针对较大样本集对硝基化合物的撞击感度进行了进一步研究。袁方强[9]等人根据分子内氢键、分子结构、对称性、氧平衡OB100、活性指数F、“拥挤性”等分子结构参数与对156个硝基类炸药的撞击感度进行了研究。房伟[10]等人选取氧系数、对称性、—COOR、氧杂环、苯环、α-H、α-OH、α-CH、硝基(—NO2)、氨基(—NH2)等作分子结构描述符，用多元线性回归计算了123个硝基化合物的撞击感度。而这些研究是凭借分子结构与撞击感度之间的定性关联，人为地发掘数个对撞击感度有影响的结构参数，因此往往构建的模型所用变量较多，或者可能存在选用参数不足以很好得表征研究的性质的问题。因此，有必要在较大样本集条件下，从分子结构角度出发对结构参数进行筛选，从而建立多硝基化合物撞击感度和其分子结构间的定量关系模型。

为了实现上述目标，这里根据QSPR基本原理，采用遗传算法[11](Genetic Algorithm，GA)对计算所得的描述符进行筛选，分别建立多元线性回归(MLR)模型和人工神经网络[12](ANN)模型对149种多硝基化合物的撞击感度定量构效关系进行研究，并进行模型比较。

2 样本与方法

2.1 试验样本

实验样本的数量和准确度直接影响撞击模型的适用性和预测精度。这里选取了149种多硝基化合物的撞击感度[13]作为实验样本，其中包含47个芳香族类化合物、70个脂肪族化合物以及32个硝胺类化合物。按照4∶1的比例随机选择120种作为训练集用于建立QSPR模型，剩余的29种作为测试集用于对所建模型进行外部评估。H50为2.5 kg落锤实验中测得的样品爆炸几率为50%时的落高，所涉及的149种多硝基化合物的撞击感度实验值(lgH50)及QSPR计算得到的预测值见附表(附表可查阅本刊网站)。由于篇幅原因，表1只给出了部分多硝基化合物的撞击感度实验值和预测值。

2.2 研究方法

首先，借助化学软件HyperChem7.5[14]进行分子结构的输入。在采用分子力学MM+初步优化的基础上，采用量子化学半经验方法PM3对分子结构进一步优化以获得能量低的稳定构型。所有计算均限制在Hartree-Fock能级，采用Ploak-Ribiere方法直至均方根误差梯度达到0.001 kJ/mol。然后将优化的分子结构导入Dragon2.1软件[15]，计算获得1481种分子描述符，将近似常数或者相关系数大于0.95的描述符删除，初步筛选获得561个分子描述符。采用Material Studio 7.0软件[16]实现遗传算法对分子描述符进行进一步筛选。继而分别采用MLR和ANN研究所得描述符与撞击感度间的定量关系，多元线性回归由SPSS软件[17]实现，人工神经网络建模由MATLAB R2014a[18]实现。试验步骤流程如图1所示。

最终，将采用相关系数(R2)、均方根误差(RMSE)和平均绝对误差(MAE)等统计参数对所建立的模型性能进行全面的评估，并采用Williams图对模型的应用域进行分析。

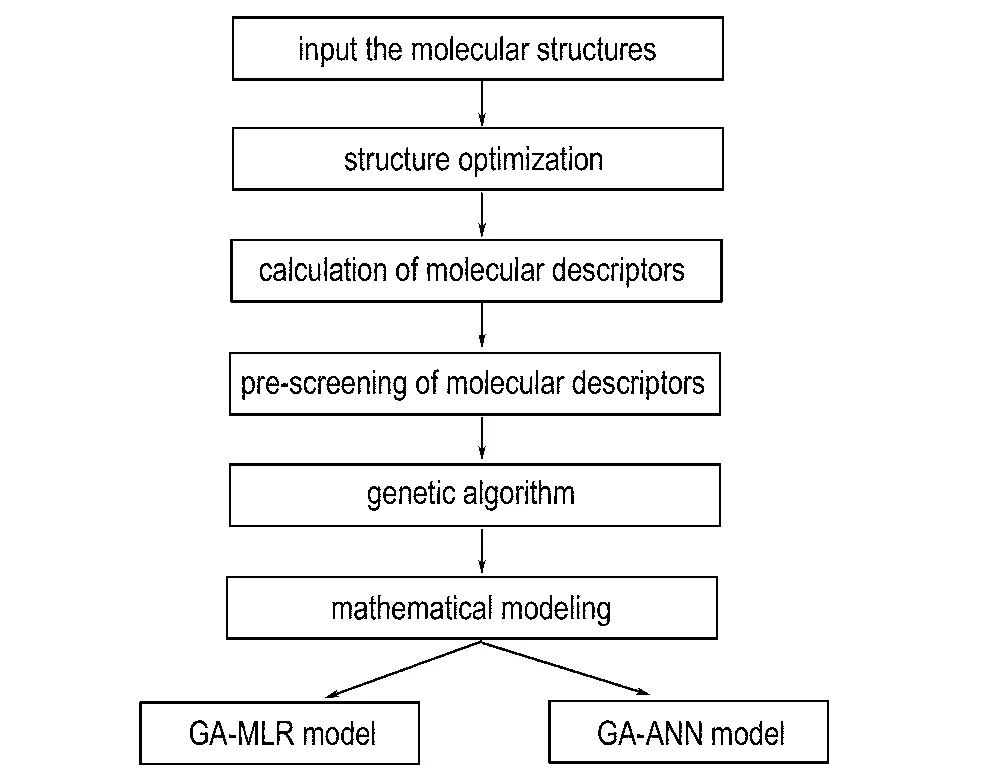
图1 QSPR研究步骤流程图

Fig.1 The flow chart of the QSPR research steps

3 结果与讨论

3.1 GA筛选结果

基于Accelrys公司的Material Studio 7.0软件，采用遗传算法(GA)对561个分子描述符进行筛选。设置方程式的初始长度6，最大方程式长度为10，种群数为50，最大代数为500，变异概率为0.1。选用Friedman提出的拟合缺失分数(Lack-Of-Fit，LOF)作为其适应度函数，比例控制LOF的平滑参数α为0.5。在遗传过程中，选择在整个种群中出现次数最多的变量为适应度函数的最优解。最终确定的6个分子描述符的名称、类型和定义见表2。

表1部分多硝基化合物的撞击感度值(lgH50)

Table 1 Impact sensitivity values of part of polynitro compounds (lgH50)

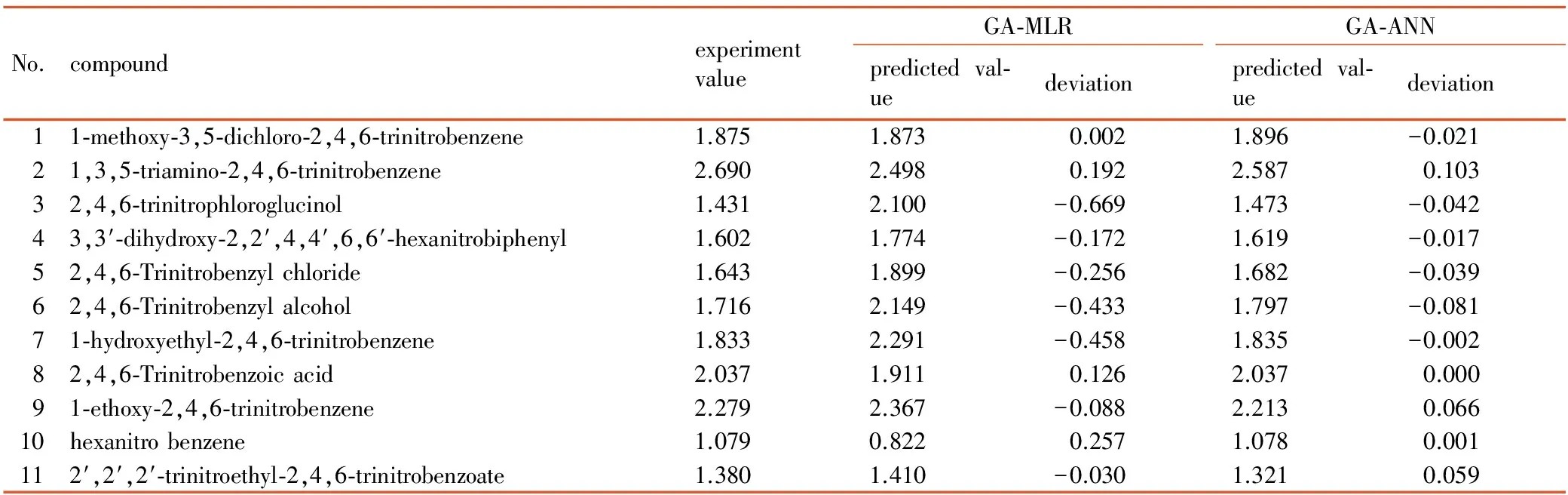
No．compoundexperimentvalueGA⁃MLRpredictedval⁃uedeviationGA⁃ANNpredictedval⁃uedeviation11⁃methoxy⁃3，5⁃dichloro⁃2，4，6⁃trinitrobenzene1．8751．873 0．0021．896-0．02121，3，5⁃triamino⁃2，4，6⁃trinitrobenzene2．6902．498 0．1922．5870．10332，4，6⁃trinitrophloroglucinol1．4312．100 -0．6691．473-0．04243，3′⁃dihydroxy⁃2，2′，4，4′，6，6′⁃hexanitrobiphenyl1．6021．774 -0．1721．619-0．01752，4，6⁃Trinitrobenzylchloride1．6431．899 -0．2561．682-0．03962，4，6⁃Trinitrobenzylalcohol1．7162．149 -0．4331．797-0．08171⁃hydroxyethyl⁃2，4，6⁃trinitrobenzene1．8332．291 -0．4581．835-0．00282，4，6⁃Trinitrobenzoicacid2．0371．911 0．1262．0370．00091⁃ethoxy⁃2，4，6⁃trinitrobenzene2．2792．367 -0．0882．2130．06610hexanitrobenzene1．0790．822 0．2571．0780．001112′，2′，2′⁃trinitroethyl⁃2，4，6⁃trinitrobenzoate1．3801．410 -0．0301．3210．059

表2 GA筛选出的描述符

Table 2 Descriptors obtained by genetic algorithm

descriptortypedefinitionIC1topologicaldescriptorsinformationcontentindex(neighborhoodsymmetryof1order)ATS1e2DautocorrelationsBroto⁃Moreauautocorrelationofatopologicalstructure⁃lag1/weightedbyatomicSandersonelectro⁃negativitiesMATS1e2DautocorrelationsMoreauautocorrelation⁃lag1/weightedbyatomicSandersonelectronegativitiesRDF050vRDFdescriptorsradialdistributionfunction⁃5．0/weightedbyatomicvanderWaalsvolumesRTuGETAWAYdescriptorsRtotalindex/unweightedR6m+GETAWAYdescriptorsRmaximalautocorrelationoflag6/weightedbyatomicmasses

3.2 GA-MLR模型的建立

首先，运用MLR研究GA筛选出的描述符和129种多硝基化合物撞击感度之间可能存在的线性关系。基于训练集所建立的撞击感度多元线性回归模型如下：

lgH50= 16.268-0.285×IC1-10.656×ATS1e-

1.578×MATS1e+0.031×RDF050v-

0.037×RTu+0.326×R6m+

SD=0.200，F=110.514，P<0.001

(1)

该模型有较高的相关系数和交互验证系数，均方根误差和标准偏差均较小，表明该模型是可靠的。模型的F检验值远大于F理论(95%置信度)=2.198，因此可以认为该回归方程及所选变量的影响均是显著的。表3所示是模型的显著性检验结果，标准系数可以确定不同分子描述符对模型的影响程度。从表3可以看出，6个描述符对撞击感度的影响大小排序为ATS1e>MATS1e>RTu>RDF050v>IC1>R6m+，所有描述符与撞击感度lgH50均呈负相关性。

表3 GA-MLR模型系数检验结果

Table 3 Test results of the coefficients of GA-MLR model

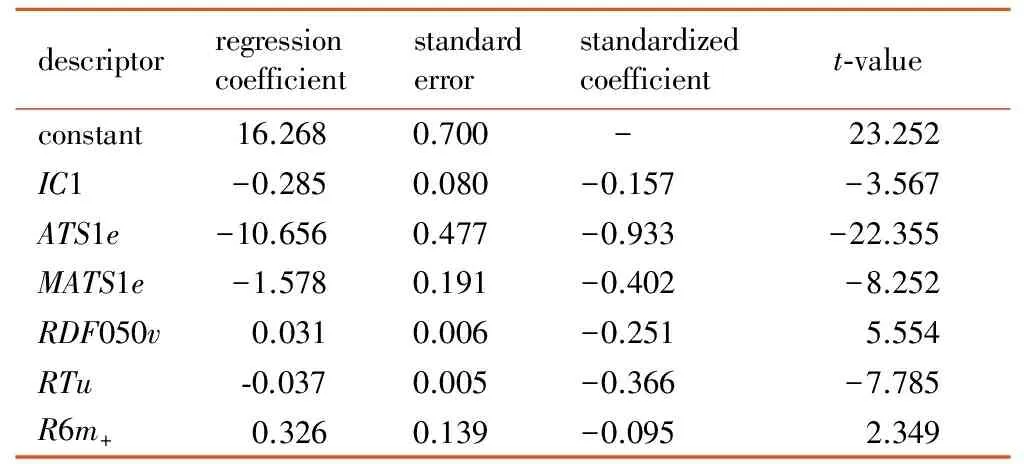
descriptorregressioncoefficientstandarderrorstandardizedcoefficient t⁃valueconstant16．2680．700 -23．252IC1-0．2850．080-0．157-3．567ATS1e-10．6560．477-0．933-22．355MATS1e-1．5780．191-0．402-8．252RDF050v0．0310．006-0．2515．554RTu⁃0．0370．005-0．366-7．785R6m+0．3260．139-0．0952．349

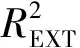
表4 GA-MLR、GA-ANN撞击感度预测模型的主要性能参数

Table 4 Main performance parameters of GA-MLR model and GA-ANN model

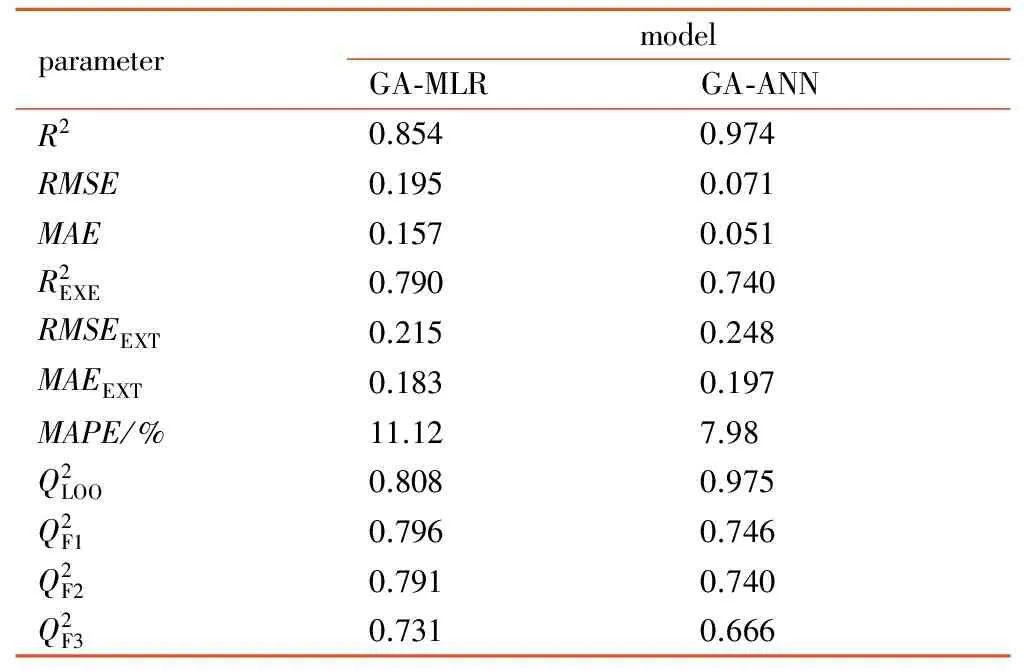
parametermodelGA⁃MLRGA⁃ANNR20．8540．974RMSE0．1950．071MAE0．1570．051R2EXE0．7900．740RMSEEXT0．2150．248MAEEXT0．1830．197MAPE/%11．127．98Q2LOO0．8080．975Q2F10．7960．746Q2F20．7910．740Q2F30．7310．666

训练集和测试集撞击感度预测值与实验值的比较及残差分布分别见图2和图3。如图2所示，所有的数据点均随机分布在对角线附近，表明此线性模型具有一定的预测能力，但是模型的精度不高，预测结果不是很好。由此猜测，多硝基类化合物的撞击感度和分子结构间可能存在非线性关系，因此将尝试建立GA-ANN非线性模型进行研究。而由图3可知，模型的预测残差均匀且随机分布于基准线的两侧。由此可以认为，GA-MLR模型在建立过程中未产生系统误差。

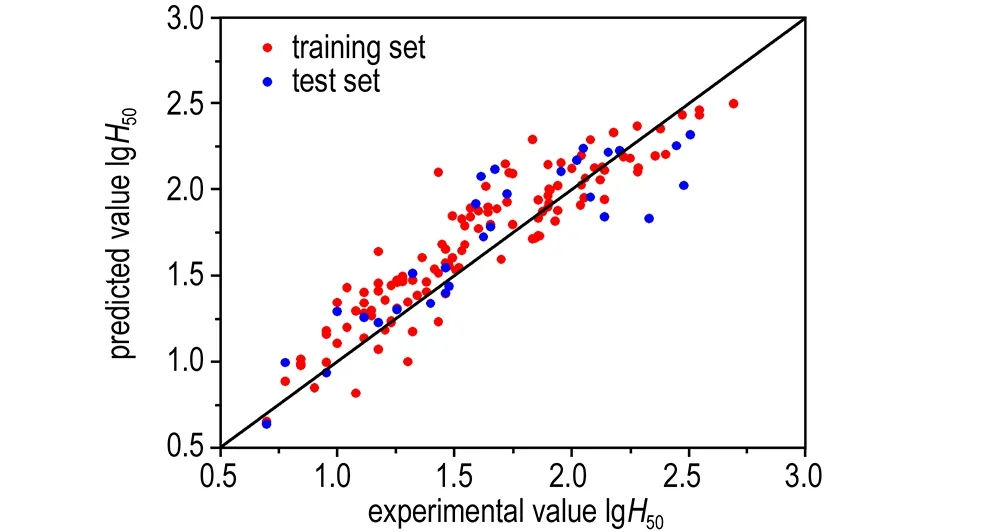
图2 GA-MLR模型所得撞击感度的预测值与实验值的比较

Fig.2 Comparison of the predicted values of impact sensitivity obtained by GA-MLR model and the experimental ones

图3 GA-MLR模型撞击感度预测值和残差的关系图

Fig.3 Relation of the predicted values of impact sensitivity obtained by GA-MLR model and the residual

3.3 GA-ANN模型的建立

在用神经网络研究化学结构性质的领域，三层反向传播的前馈神经网络应用最为广泛。理论上已经证明：具有偏差和至少一个S型隐含层加上一个线性输出层的网络，能够逼近任何有理函数[12]。因此，这里建立包含输入层、输出层和一层输隐含层的三层BP人工神经网络用于非线性模型研究。BP神经网络的构建在MATLAB R2014a环境中实现，经过多次训练试验，最终确定6-8-1的神经网络结构的精度最好。具体参数设定如下：输入层节点数为6，隐含层节点数为8，输出层节点数为1，选择最小训练速率0.1，最大迭代次数为1000，隐含层激活转移函数采用双曲正切S型函数tansig，输出层激活转移函数采用线性函数purelin，训练函数采用trainlm，网络学习函数采用带动量项的BP学习规则learngdm。

模型的预测结果见附表，相关模型性能参数见表4。计算得到，该模型的相关系数为0.974，交叉验证系数为0.975，训练集和测试集的均方根误差分别为0.071和0.248，平均绝对误差分别为0.051和0.197。从相关系数、交互验证系数和均方根误差来看，GA-ANN模型的精度明显高于GA-MLR模型。

如图4所示，所有多硝基化合物撞击感度预测值和实验值的比较均未偏离对角线很远，整体基本紧挨对角线，这说明该模型比MLR建立的模型精度高。图5给出了GA-ANN模型的残差图，预测残差均匀且随机分布于基准线，该模型在建立过程中未产生系统误差。

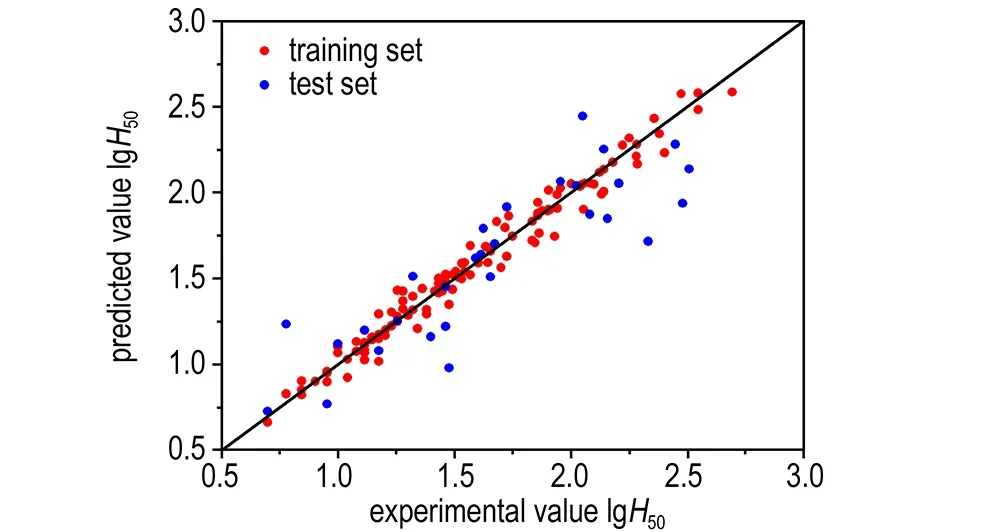
图4 GA-ANN模型所得撞击感度预测值与实验值的比较

Fig.4 Comparison of the predicted values of impact sensitivity obtained by GA-ANN model and the experimental ones

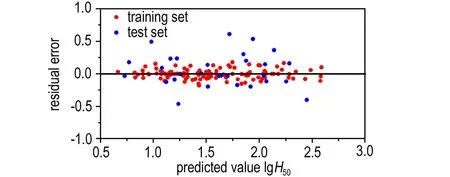
图5 GA-ANN模型撞击感度预测值和残差的关系图

Fig.5 Relation of the predicted values of impact sensitivity obtained by GA-ANN model and the residual

3.4 模型比较

这里采用Williams图[19]进一步分析比较两个模型的应用域。横坐标为臂比值，纵坐标为标准残差。标准残差落在(-3，+3)以外的化合物，认为其实验值是离群点; 当化合物的臂比值hi大于警戒值h*时，认为该物质显著影响模型的回归效果[14]。臂比值的计算式如下：

(2)

警戒值h*的表达式如下：

h*=3×(m+1)/n

(3)

式中，m为建立模型所用变量的个数。

如图6、图7所示的Williams图中，GA-MLR模型和GA-ANN模型分别有2个物质和5个物质的标准残差落在了基准线以外，其相应的化合物和撞击感度值见表5和表6。

观察表5、表6发现，出现异常值的物质其撞击感度的预测残差均较大，这表明，建模所用的参数没能很好的表征其撞击感度。已有研究表明[20]，除了分子结构外，含能材料的感度还与炸药晶体特性密切相关，如颗粒内部空洞的微观结构、颗粒表面缺陷、颗粒大小及分布、颗粒形状和表面光滑度对感度影响非常显著。因此，仅用分子结构参数来表征撞击感度还不够完善。而2′,2′-二硝基丙基-2,4,6-三硝基苯甲酸酯的标准残差在两个模型中同时出现异常，可认为主要原因是其实验值数据本身不够准确。在表7中，六硝基苯的臂比值超出了警戒值，这表明，六硝基苯显著影响了模型的回归效果，可以认为其结构相对于整个样本集而言是比较特殊的。

将所建的两个模型与几种已有的多硝基化合物撞击感度QSPR模型进行比较，相关统计参数见表8。

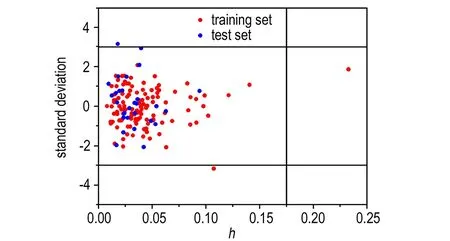
图6 GA-MLR撞击感度模型的Williams图

Fig.6 Williams plot of GA-MLR model for impact sensitivity

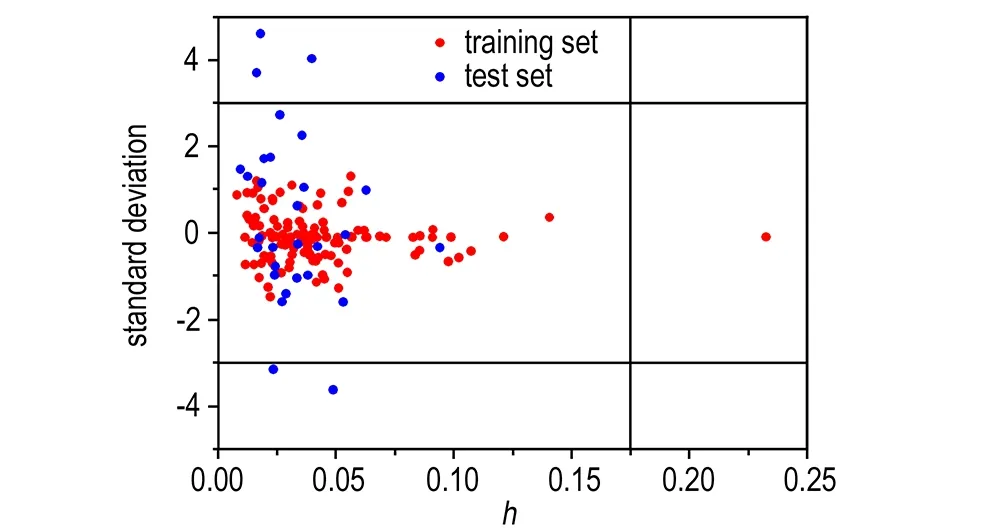
图7 GA-ANN撞击感度模型的Williams图

Fig.7 Williams plot of GA-ANN model for impact sensitivity

表5根据残差判定的GA-MLR模型中的异常值

Table 5 Outliers of GA-MLR model determined according to the residual

compoundstandardizedresidualexperimentalvaluepredictedvalueresidualerror2，4，6⁃trinitrophloroglucinol-3．1681．4312．100-0．6692′，2′⁃dinitropropyl⁃2，4，6⁃trinitrobenzoate3．1662．3301．8330．497

表6根据残差判定的GA-ANN模型中的异常值

Table 6 Outliers of GA-ANN model determined according to the residual

compoundstandardizedresidualexperimentalvaluepredictedvalueresidualerror2′，2′⁃dinitropropyl⁃2，4，6⁃trinitrobenzoate4．6112．3301．7180．612trinitroethyl⁃bis⁃(trinitroethoxy)⁃acetate-3．6190．7781．237-0．459N⁃(2⁃propyl)⁃trinitroacetamide-3．1492．0492．447-0．398bis⁃(2，2，2⁃trinitroethyl)⁃succinate3．7111．4770．9820．495bis⁃(2，2⁃dinitropropyl)⁃carbonate4．0392．4771．9400．537

表7根据臂比值判定的撞击感度预测模型中的异常值

Table 7 Outliers of predicted model of impact sensitivity determined according to the arm ratio

compoundh∗hexperimentalvaluepredictedvalueresidualerrorhexanitrobenzene0．1750．2321．0791．0780．001

表8所建模型与已有模型的比较

Table 8 Comparison between the established models with the existing models

authormodeldatasetR2Q2LOORMSEEXTthispaperGA⁃MLR1490．8540．8080．215GA⁃ANN(6⁃8⁃1)1490．9740．9750．248Nefati[21](1995)ANN(13⁃2⁃1)2040．7940．7950．257WangRui[22](2008)MLR1560．7710．5930．251ANN(16⁃12⁃1)1560．816-0．247GuillaumeFayet[23](2012)MLR1610．8160．7930．230

本文建模采用的是由GA筛选获得分子描述符，因此能更系统全面地表征所研究的性质，且模型中涉及的变量个数远少于已有模型。比较各模型的相关系数、交互验证系数和外部验证的均方根误差，可以认为这里获得的GA-MLR模型和GA-ANN模型明显优于已有模型。

4 结 论

(1)运用遗传算法筛选出6个分子描述符，分别构建了149种多硝基化合物撞击感度的GA-MLR 模型和 GA-ANN 模型，结果表明两个模型均是稳定可靠的;

(2)所得GA-ANN模型明显优于GA-MLR模型，说明多硝基化合物的撞击感度与分子结构间存在较强的非线性关系，且两个模型的预测精度均高于已有的QSPR模型;

(3)由于落锤实验受诸如晶体特性、环境等其他因素的影响，因此所建的两个模型虽然具有一定的预测能力，但是预测效果仍有继续完善的空间。

参考文献:

[1] 金韶华，王伟，松全才，等. 含能材料机械撞击感度判据的认识和发展[J]. 爆破器材, 2006, 35(6): 11-14.

JIN Shao-hua, WANG Wei, SONG Quan-cai, et al. Understanding and development of criteria of impact sensitivity of energetic materials[J].ExplosiveMaterials, 2006, 35(6): 11-14.

[2] Katritzky A R, Lobanov V S, Karelson M. QSPR: The correlation and quantitative prediction of chemical and physical properties from structure[J].ChemicalSocietyReviews, 1995, 24(4): 279-287.

[3] 赵俊，何碧，程新路，等. 多硝基炸药撞击感度与分子特征量关联度的BP神经网络方法研究[J]. 四川大学学报(自然科学版), 2006, 17(5): 501-507.

ZHAO Jun, HE Bi, CHENG Xin-lu, et al. Neural networks study on the correlation between impact sensitivity and molecular structures for nitramines[J].AtmosphericChemistry&Physics, 2006, 17(5): 501-507.

[4] 王睿, 蒋军成, 潘勇, 等. 电性拓扑态指数预测硝基类含能材料撞击感度[J]. 固体火箭技术, 2008, 31(6): 657-662.

WANG Rui, JIANG Jun-cheng, PAN Yong, et al. Prediction on impact sensitivity of nitro energetic materials by means of electrotopological state indices[J].JournalofSolidRocketTechnology, 2008, 31(6): 657-662.

[5] 王睿, 蒋军成, 潘勇. 脂肪族硝基含能化合物撞击感度的QSPR研究[J]. 南京工业大学学报 (自然科学版), 2011, 33(3): 15-21

WANG Rui, JIANG Jun-cheng, PAN Yong. Impact sensitivity analysis on aliphatic nitro energetic compounds by QSPR[J].JournalofNanjingUniversityofTechnology, 2011, 33(3) : 15-21.

[6] 葛素红, 孙桂华, 董光兴. 硝基芳香族炸药的分子结构和撞击感度关系研究[J]. 四川师范大学学报, 2014(5): 684-690.

GE Su-hong, SUN Gui-hua, DONG Guang-xing. Molecular structure, atomization energy and impact sensitivity of eighteen trinitro-aromatic-explosives[J].JournalofSichuanNormalUniversity, 2014(5): 684-690.

[7] Fayet G, Rotureau P, Joubert L, et al. Development of a QSPR model for predicting thermal stabilities of nitroaromatic compounds taking into account their decomposition mechanisms[J].JournalofMolecularModeling, 2011, 17(10): 2443-2453.

[8] Badders N R, Wei C, Aldeeb A A, et al. Predicting the impact sensitivities of polynitro compounds using quantum chemical descriptors[J].JournalofEnergeticMaterials, 2006, 24(1): 17-33.

[9] 袁方强，蔡从中，赵帅. 用结构参数预测硝基类炸药的撞击感度[J]. 爆炸与冲击, 2013, 33(1): 79-84.

YUAN Fang-qiang, CAI Cong-zhong, ZHAO Shuai. Prediction of impact sensitivity of nitro energetic compounds by using structural parameters[J].Explosion&ShockWaves, 2013, 33(1): 79-84.

[10] 房伟，王建华，刘玉存，等.多因素预测硝基化合物的撞击感度[J]. 火炸药学报, 2014, 37(5): 42-46.

FANG Wei, WANG Jian-hua, LIU Yu-cun, et al. Multivariate prediction of impact sensitivity of nitro compounds[J].ChineseJournalofExplosives&Propellants, 2014, 37(5): 42-46.

[11] 陈国良，王煦法，庄镇泉，等. 遗传算法及其应用[M].北京: 人民邮电出版社, 1999: 2-4.

CHEN Guo-liang, WANG Xu-fa, ZHUANG Zhen-quan,et al. Genetic algorithm and its application[M]. Beijing:Posts & Telecom Press, 1999: 2-4.

[12] 丛爽. 面向MATLAB工具箱的神经网络理论与应用第三版[M]. 合肥: 中国科学技术大学出版社, 2009: 72-81.

CONG Shuang. The neural network theory and application facing the toolbox of MATLAB of the third edition [M]. Hefei:Press of University of Science and Technology of China, 2009: 72-81.

[13] Storm C B, Stine J R, Kramer J F. Sensitivity relationships in energetic materials[J].ChemistryandPhysicsofEnergeticMaterials, 1990: 605-639.

[14] SHI Jing-jie, Chen L P, Chen W H. QSPR models of compound viscosity based on iterative self-organizing data analysis technique and ant colony algorithm[J].ActaPhysico-chimicaSinica, 2014, 30(5): 803-810.

[15] Tebby C, Mombelli E, Pandard P. et al. Exploring an eco toxicity database with the OECD (Q)SAR toolbox and DRAGON descriptors in order to prioritize testing on algae, daphnis, and fish[J].ScienceoftheTotalEnvironment, 2011, 409: 3334-3343.

[16] SHI Jing-jie. Prediction of auto-ignition temperatures of organic compounds by SVM based on the genetic algorithm[J].JournalofChinaSafetyScience, 2011, 21(7): 125-129.

[17] 薛薇. 统计分析与SPSS的应用(第三版)[M]. 北京: 中国人民大学出版社, 2011.

XUE Wei. Statistical analysis and the application of SPSS (3rd edition)[M]. Beijing: China Renmin University Press, 2011.

[18] 王小川. MATLAB神经网络43个案例分析[M]. 北京:北京航空航天大学出版社, 2013.

WANG Xiao-chuan. 43 cases analysis of MATLAB neural network[M]. Beijing:University Press, 2013.

[19] Gramatica P. Principles of QSAR models validation: internal and external[J].QSARandCombinatorialScience, 2007, 26(5): 694-701.

[20] 李洪珍，康彬，李金山，等. RDX晶体特性对冲击感度的影响规律[J]. 含能材料, 2010, 18(5): 487-491.

LI Hong-zhen, KANG Bin, LI Jin-shan, et al. Effects of RDX crystal characteristics on shock sensitivities [J].ChineseJournalofEnergeticMaterials(HannengCailiao), 2010, 18(5): 487-491.

[21] Nefati H, Cense J M, Legendre J J. Prediction of the impact sensitivity by neural networks[J].JournalofChemicalInformation&Modeling, 1996, 36(4): 804-810.

[22] Wang Rui, Jiang Jun-cheng, Pan Yong, et al. Prediction of impact sensitivity of nitro energetic compounds by neural network based on electro topological-state indices[J].Hazard.Mater, 2009, 166: 155-186.

[23] Fayet G, Rotureau P, Prana V, et al. Global and local quantitative structure-property relationship models to predict the impact sensitivity of nitro compounds[J].AICHE, 2012, 31(3): 291-303.