基于遗传算法的BP神经网络隧道施工参数正反演分析与应用

王 睿, 漆泰岳, 冯 剑, 雷 波, 李 延

(1. 西南交通大学 交通隧道工程教育部重点实验室,四川 成都 610031; 2. 西南交通大学 土木工程学院, 四川 成都 610031; 3. 中国市政工程西南设计研究总院有限公司, 四川 成都 610031)

随着隧道施工过程中信息化程度和监控手段的不断提高，现已实现监控信息的高效采集。但隧道施工中出现环境变化后的施工参数优化仍停留在被动应对阶段，相应的运算检验过程繁复，而且相对滞后。因此，实现高效的反馈修正是目前隧道施工面临的一个重要问题。

目前，围岩参数反演分析的研究主要集中在岩石物理性质方面，即利用实测数值，反推获得所需参数。文献[1-3]对隧道施工中的弹性模量和数值模拟进行反演分析。易小明等[4]对岩体弹性模量和松动圈弹性模量进行反演分析。李培现[5]基于正交设计建立模型将弹性模量和抗拉强度作为反演参数。宋战平等[6]对弹性模量、泊松比和黏聚力进行反演参数的稳定性分析。这种预测与分析，需通过实测值的反演分析得到参数，再建立模型进行计算分析，耗时较长，对于时效性要求高的隧道开挖较不利。而且在实际工程中，隧道变形是围岩与支护共同作用的结果，设计初期将隧道所在地域划分为几个典型区段且认为每区段岩土参数基本一致，实际的隧道变形值与该区段的支护方式(施工工艺)直接相关。

基于此，本文结合实例工程区段，在施工方法既定的前提下，通过对施工工艺进行分类，利用正交表并结合FLAC3D有限差分模型，计算代表性隧道施工工艺参数下得到的隧道变形值的样本集。BP神经网络作为最广泛使用的人工神经网络之一，结构严谨，可操作性强，可实现高度非线性映射，但易出现局部最小；遗传算法可同时对多个可行解进行检查，不会陷入局部最小。因此通过将BP神经网络与遗传算法相结合的方法，建立基于施工工艺与隧道变形值相互联系的Matlab程序，通过算例验证该方法在施工工艺参数选定方面的可行性。

1 基于遗传算法优化的BP神经网络

1.1 BP神经网络

BP算法的学习过程通过信息的正向传递与误差的反向传播修正两个过程实现。数据从输入层经隐含层逐层向后传播；训练网络权值时，则沿着减少误差的方向，从输出层经过中间各层逐层向前修正网络的连接权值。随着学习的不断进行，使误差达到要求精度或者达到预先设定的学习次数为止。

BP神经网络由输入层、输出层和一个或多个隐含层组成，结构如图1所示。

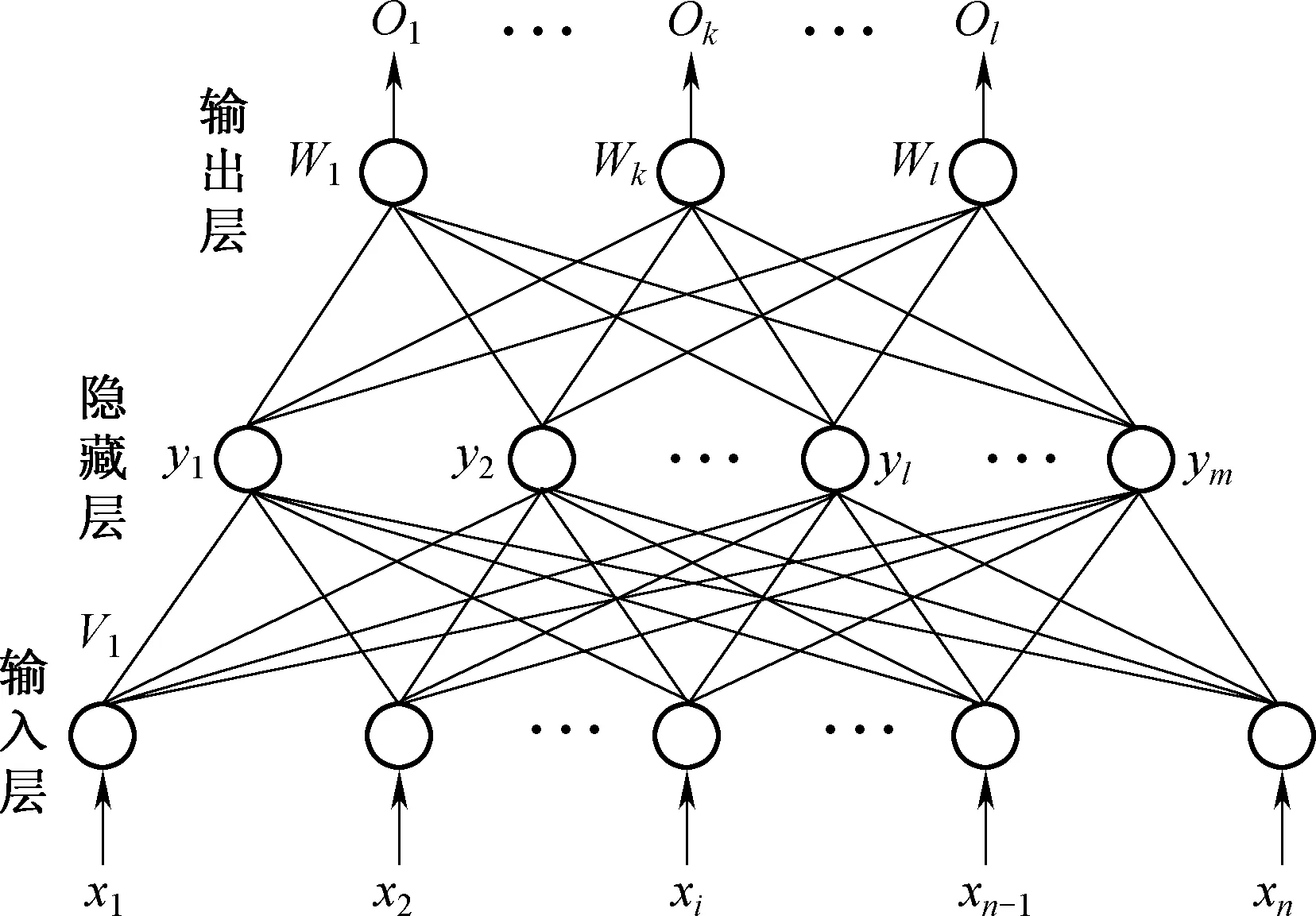
图1 BP神经网络结构简图

用BP神经网络模拟思路步骤如下：

(1)构造输入节点数n、隐含层节点数m、输出节点数为l的网络。

(2)构造网络训练样本。其输入参数使用正交设计方法构造，输出参数为输入参数对应的模拟计算值。

(3)构造测试样本。测试使用训练样本训练形成的网络预测能力。

1.2 遗传算法

遗传算法是一种借鉴生物界自然选择和自然遗传机制的随机搜索算法。与传统的优化算法相比，遗传算法对参数的编码而非参数本身进行操作；从多点开始并行操作，而非局限于一点，因此可以有效防止搜索过程收敛于局部最优解；算法通过目标函数计算适值，不需要其他推导和附加信息，对问题的依赖性较小；寻优规则由概率决定。遗传算法描述如下[7]：

(1)确定编码方案；

(2)初始化群体(确定遗传参数)；

(3)计算个体适应度；

(4)进行遗传算子操作(选择、交叉、变异)，产生新一代个体；

(5)返回(3)，直至达到遗传代数或者适应度要求。

1.3 基于遗传算法优化的BP神经网络

BP神经网络具有较强的分类识别功能，识别速度快而且准确[8,9]，但存在易陷入局部极小的不足，会引起收敛速度慢和振荡效应等。在实际计算过程中可以通过调整初始权值来解决局部极小问题。对于支护参数反演而言，每个待定参数都有一定的变化范围，而BP网络不能将反演参数进行范围界定，从而使一些参数反演值不符合实际。由于遗传算法宏观搜索能力强且具有鲁棒性强、并行运算的特点，因此可以用它完成BP算法初始权值的确定，来克服BP算法的缺点。基于遗传算法的BP神经网络，就是利用Matlab编程将二者的优点结合起来：用神经网络仿真拟合来寻找非线性数据之间的响应关系，再通过遗传算法寻找最优解。具体流程[10]如图2所示。

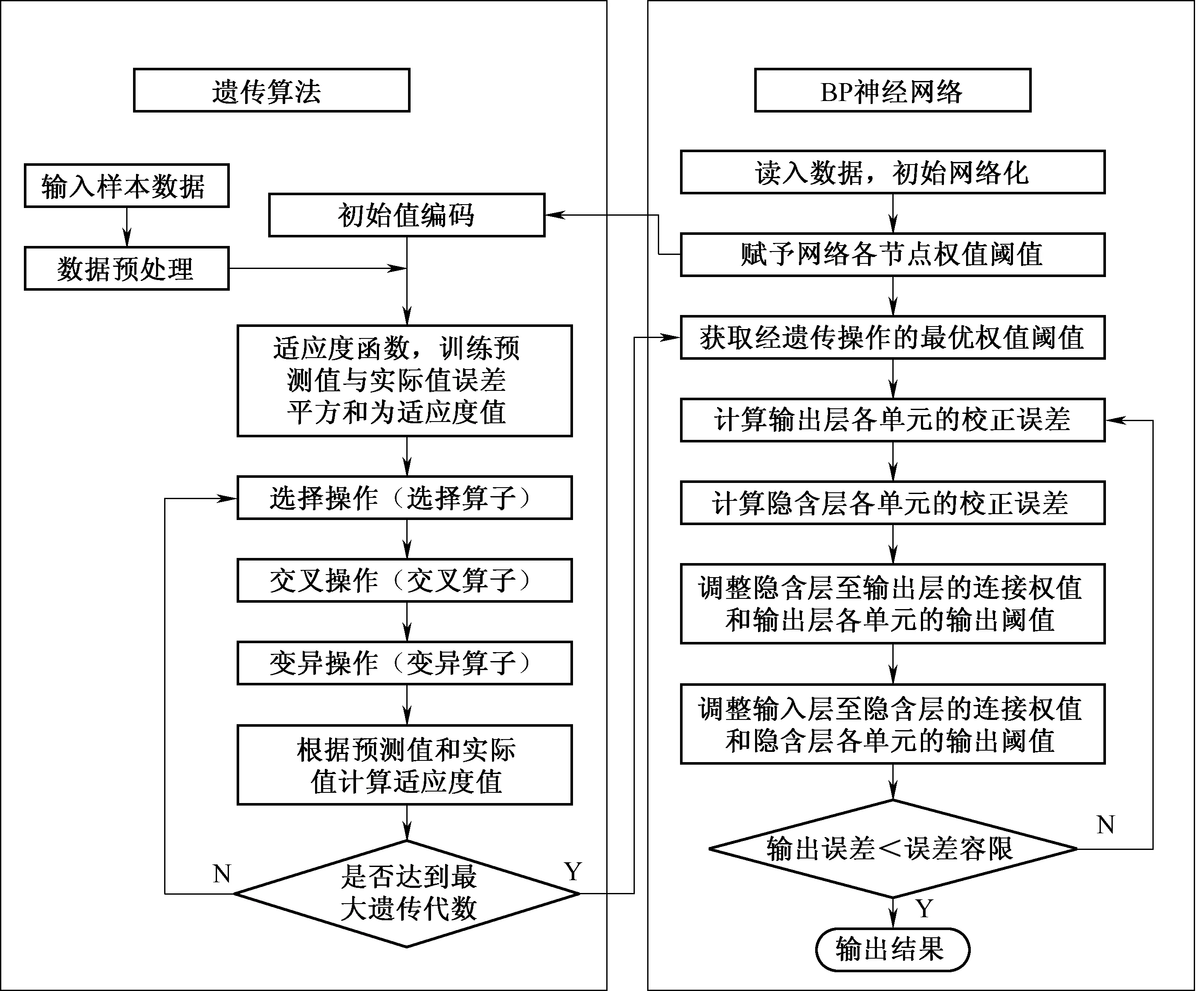
图2 算法流程图

2 工程概况与样本的建立

2.1 工程概况与数值模型的建立

某隧道位于低山丘陵区，地形起伏不大，冲沟较发育，工地内地层从上至下分为三层：第四系上更新统风积砂质黄土，下伏第三系上新统泥岩和二叠系上统砂岩泥岩互层。土层参数见表1。

该隧道总长525 m，Ⅴ级围岩，隧道最大开挖深度

10.39 m，最大开挖宽度11.56 m，采用CRD法开挖。这里选择较为软弱的Ⅴ级围岩某典型断面作为样本试验段，利用有限差分软件FLAC3D建立模型，模型尺寸100 m×50 m×110 m，共有86 400个单元，如图3、图4所示。

表1 围岩土层参数取值

图3 模型正面及土体分部情况

图4 CRD法开挖断面及开挖顺序示意图

开挖顺序及支护方式如图5、图6所示。这里初期支护的喷射混凝土采用实体单元模拟，二次衬砌采用shell单元，横向、纵向临时支撑、仰拱等支护均采用实体单元模拟。

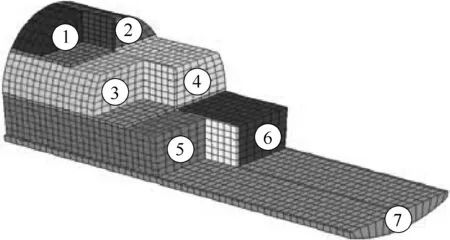
图5 CRD法开挖方式示意图

(a)隧道开挖内部支护示意图

(b)隧道开挖锚杆支护示意图图6 隧道开挖支护示意图

为了建立相对全面的施工参数范围，通过对相同黄土土层下几个隧道的工程类比分析及施工作业空间的要求[11-14]，得出该工艺施工中可能用到的施工参数有开挖台阶高度、锚杆长度、二次衬砌施作间距、初期衬砌混凝土强度等级，其分布情况见表2。

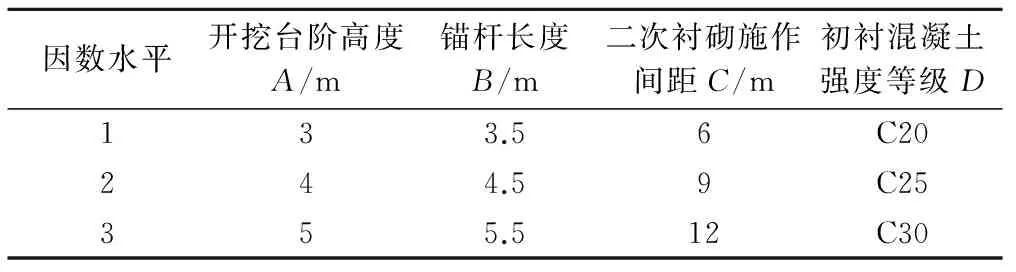
表2 隧道支护参数取值

2.2 基于正交试验样本集的建立

正交试验设计是利用正交表安排与分析多因素试验的一种设计方法[15]。它在试验因素的全部水平组合中，挑选部分有代表性的水平组合进行试验，通过对这部分试验结果的分析了解全面试验情况[16]，找出最优组合。这种试验模式避免了多因素多水平全部试验庞大的试验量，也能较全面反映试验的所有可能情况。由于混凝土结构设计规范上无泊松比的明确规定，不同等级混凝土的泊松比数据多在0.17～0.23之间，通常建议采用0.20[17,18]。本文初期衬砌强度采用弹性模量值表示，见表3中初衬强度一项。

为了使神经网络的拟合分析更准确，这里选取试验数量较多的正交表L27(313)，并结合实际工程建立有限差分模型进行计算，得到具有代表性的四个变形值：拱顶沉降、拱底隆起、上开挖断面收敛(上收敛)、下开挖断面收敛(下收敛)，具体工程中开挖断面的监测点布置如图7所示。

表3 试验样本及计算结果

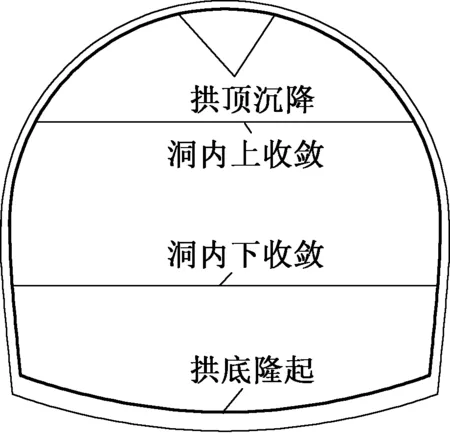
图7 隧道断面监测点示意图

通过正交表得出试验样本，再通过FLAC3D进行模拟计算，结果见表3。

3 正反演分析及应用

3.1 遗传算法与BP神经网络参数选取

利用Matlab按图2进行编程，其中BP神经网络与遗传算法中的参数选择分别见表4、表5。

表4 BP神经网络参数

表5 遗传算法参数

3.2 正反演实现及准确性分析

基于已完成工程进行的非线性拟合演算，工程实测值与Matlab程序演算值的匹配程度是决定正反演分析方法可行性的基础。

正演分析，即利用支护参数来预测沉降值。已知实际工程的施工参数为：开挖台阶3 m，锚杆长度3.5 m，二次衬砌施作距离10 m，喷射混凝土强度C20，通过正演分析Matlab程序演算及FLAC3D模型计算，其结果见表6。

表6 实测值、演算值及模型计算值的比较

注：相差值△1由程序演算值与实测值之差除以实测值得到；相差值△2由模型计算值与演算值之差除以演算值得到。

演算值与实测值的匹配度达到85%就基本能满足工程要求[19]，从表3可以看出，拱顶沉降、上收敛值、下收敛值均满足精度需要；由于受施工工艺的影响，拱底隆起测量的时间相对滞后，隆起量实测值可能偏小。正演分析演算值与实测值较吻合，适合工程应用。

反演分析，即基于施工工艺已定、施工参数值可以调整的情况，利用沉降值对支护形式进行预测。利用反演分析Matlab程序演算和模型进行计算，其结果比较见表7。

表7 实测值与演算值的比较

由于实际参数的取值通常为整数，演算值得出后，出于安全考虑通常按偏安全取整，详见表7中的演算值取整一项。将表7中的“演算值取整”分别带入正演分析Matlab程序和FLAC3D模型中可得演算值与模型计算值的差异，见表8。

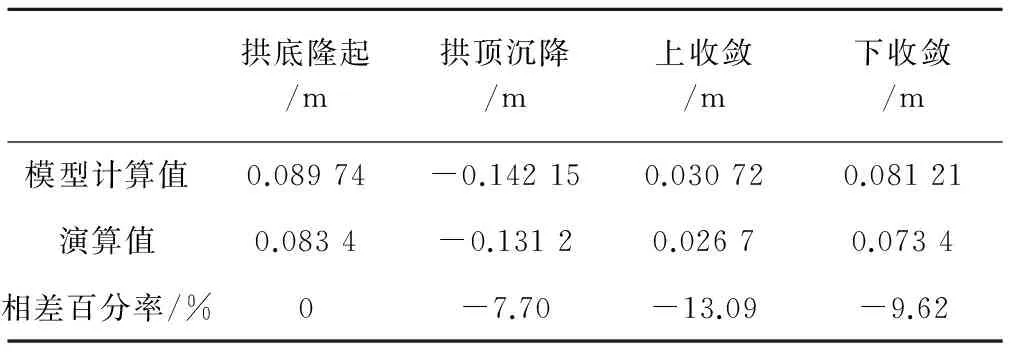
表8 模型计算值与演算值的比较

从表7、表8可知，反演分析Matlab程序的演算值与实测值及正演分析Matlab程序的演算值与模型计算值误差都在15%以内，能够满足工程精度要求。

3.3 施工过程中的正演分析及应用

施工过程中由于各种原因造成的工艺改变很常见，通常对于这些工艺参数改变的分析计算耗时较长，而施工过程中的时间通常比较宝贵，一方面是工程工期的限制，也为了避免围岩过度松弛产生安全隐患，确保施工安全。故避免长时间计算与分析就更重要，基于遗传算法的BP神经网络提供了一种便捷快速、相对准确的方法。具体的工程应用见表9。

表9 正演分析在实际工程施工中的应用

由表9可以看出，实测值与演算值除拱底隆起偏差较大外，其余相差百分率都在10%以内，具有较高的准确度，实际施工中如果采用该正演分析方法将有效提高工程变更的时效性。当然对于变更和质量缺陷，除了变形控制指标外，还有土体和结构强度指标，但是该方式对于施工过程的可能变化情况提供了及时有效的参考，具有较高的工程实际使用价值。

3.4 施工过程中的反演分析及应用

目前隧道设计的主要目标是安全、经济、美观适用[20,21]。强调安全就必须加强结构支护，增大安全系数，若强调经济，就要节省材料，降低安全系数，因此需要一个合理的平衡点，既能保证安全又能满足经济性目标。反演分析从隧道变形的角度提供了一种有效方法。

对于本文的黄土地层隧道，由于其土质较软，根据工程类比及计算，开挖预留量初步设定为30 cm。结构计算中，安全系数K通常取2，为保持整体安全系数的一致性，文中将安全系数K取2进行试验性反演计算，控制沉降值取15 cm。根据实测及FLAC3D模型计算结果选取一组变形值(拱底隆起、拱顶沉降、上收敛、下收敛)分别为0.08、0.15、0.04、0.08 m，根据反演分析Matlab程序计算结果见表10。

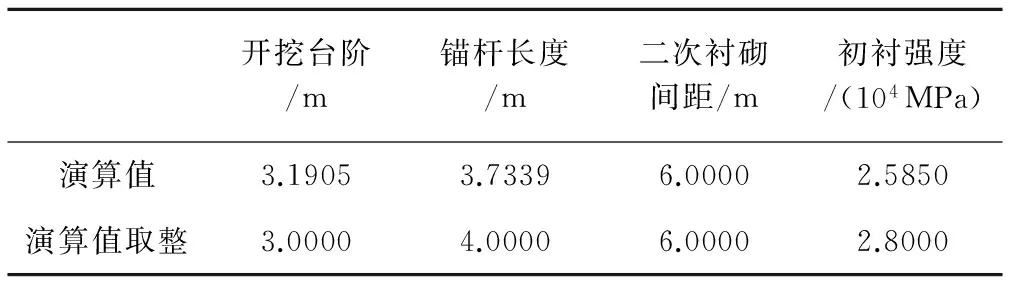
表10 反演程序计算所得支护参数

为验证“演算值取整”的可靠性，将其带入正演分析Matlab程序进行正演计算，同时将参数代入FLAC3D模型中计算，结果见表11。

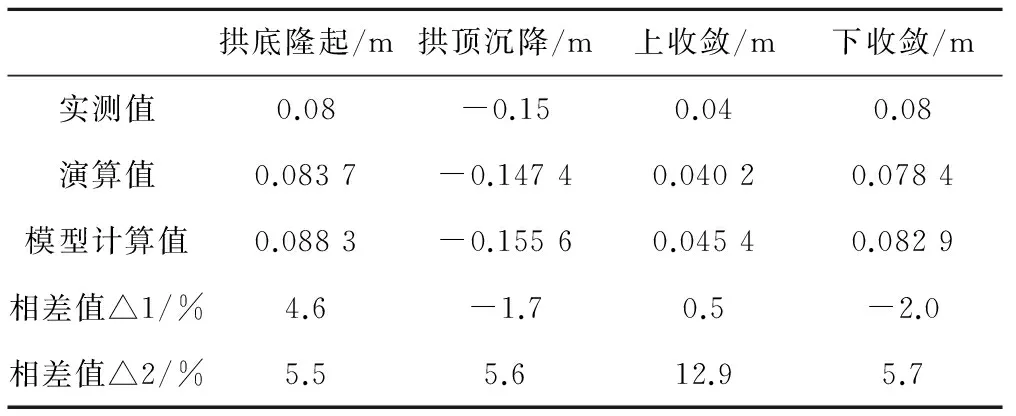
表11 正演程序及数值模型计算所得变形值对比

注：相差值△1由演算值与实测值之差除以实测值得到；相差值△2由模型计算值与演算值之差除以演算值得到。

从表11可以看出，反演分析的施工参数计算是有效的，符合工程精度要求。反演施工参数(演算值取整)与实际施工参数的比较见表12。

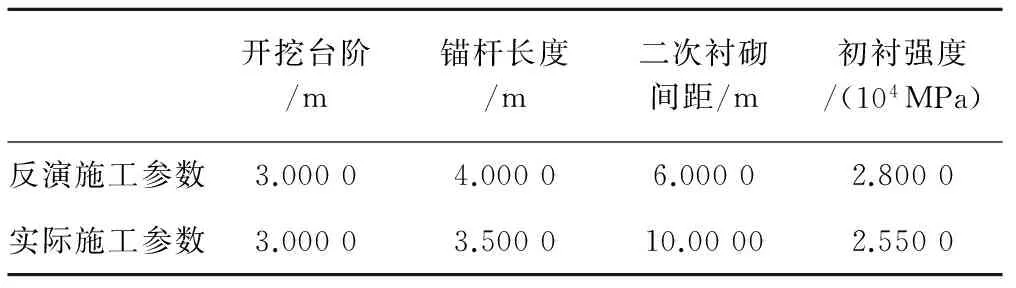
表12 反演优化参数与实际施工参数对比

实际施工最大沉降值为0.178 2 m，采用反演参数得到的沉降演算值为0.147 4 m，相差近20%；施工参数方面，反演施工参数锚杆长度增加了约14%，强度由C20变为C25，但二衬的施作间距由10 m缩短为6 m，缩短了40%，反演分析获得的参数通过提高的初期衬砌强度控制沉降值，同时缩短了隧道完成时间，从对位移的控制来看，反演分析Matlab程序能够较准确地得到控制位移下的施工参数，为实际施工提供有效指导，具有较强实际意义。

4 总结

本文利用正交试验方法，基于实际工程建立三维数值模型进行数值计算得到样本集，采用该样本集结合基于遗传算法的BP学习算法形成训练网络(Matlab程序)，实现针对实际隧道工程施工参数优化的正演分析和反演分析。

正演分析，即利用支护参数来预测沉降值，虽然前期建立程序需要大量的样本计算，但隧道建设前期时间相对充裕，实际施工开始后，通过建立的正演分析Matlab程序能够对施工过程中遇到的突发情况或者质量缺陷，实现高效且相对准确的沉降预测，提高了工程应对变化的能力，有效减少时间引起的安全风险，对于指导实际工程施工具有一定参考意义。

反演分析，即利用沉降值来反向计算支护参数，对于隧道净空控制较高，或者经济性要求高的工程，该方法可以通过多次选择意向变形控制值，实现最优支护参数的寻找，有效减少模型计算量，同时对于隧道设计，能够提供相对优选的参数选项，避免了计算分析的盲目性。

本文依托实际工程案例和工程地质条件提出隧道工程施工参数正反演分析方法，其数据及由此得出的结论对于类似工程具有参考意义，分析计算的过程和方法也可以类比应用到其他工程中，用以改良设计及施工方式、过程；参数的选取及讨论不够充分，对于施工中各种因素的考虑还不够全面，有待进一步研究和学习。

参考文献：

[1]董呈龙. 基于监控量测和数值模拟的隧道围岩参数反演分析[D]. 武汉: 武汉理工大学, 2009.

[2]周学良. 隧道围岩变形监测与围岩参数的反演分析[D]. 合肥:合肥工业大学, 2007.

[3]倪绍虎, 肖明. 基于围岩松动圈的地下工程参数场位移反分析[J]. 岩石力学与工程学报，2009，28(7)：1 439-1 446.

NI Shaohu, XIAO Ming. Displacement Back Analysis of Parameter Field in Underground Engineering Based on Excavation Damaged Zone of Surrounding Rock[J]. Chinese Journal of Rock Mechanics and Engineering, 2009, 28(7): 1 439-1 446.

[4]易小明, 陈卫忠, 李术才, 等. BP神经网络在分岔隧道位移反分析中的应用[J]. 岩石力学与工程学报, 2006, 25(S2):3 927-3 932.

YI Xiaoming, CHEN Weizhong, LI Shucai, et al. Application of BP Neural Network to Back Analysis of Forked Tunnel Displacement[J]. Chinese Journal of Rock Mechanics and Engineering, 2006, 25(S2): 3 927-3 932.

[5]李培现. 开采沉陷岩体力学参数反演的BP神经网络方法[J]. 地下空间与工程学报, 2013, 9(S1): 1 543-1 548,1 579.

LI Peixian. Rock Mass Mechanical Parameters Inversion of Mining Subsidence Using BP Neural Network[J]. Chinese Journal of Underground Space and Engineering, 2013, 9(S1)：1 543-1 548, 1 579.

[6]宋战平, 刘京, 梁莉, 等. 基于差异进化算法反演参数的隧道稳定性分析[J]. 地下空间与工程学报, 2013, 9(3): 558-565.

SONG Zhanping, LIU Jing, LIANG Li, et al. Structure Stability Analysis of Motianling Shaft Tunnel Based on Parameters Back Analysis of Differential Evolution Method[J]. Chinese Journal of Underground Space and Engineering, 2013,9(3):558-565.

[7]周翔, 朱学愚, 文成玉, 等. 基于遗传学习算法和BP算法的神经网络在矿坑涌水量计算中的应用[J].水利学报,2000(12):59-63.

ZHOU Xiang, ZHU Xueyu, WEN Chengyu, et al. Application of ANN to Predict the Drainage in Mine[J]. Journal of Hydraulic Engineering, 2000(12): 59-63.

[8]王志亮, 李筱艳, 殷宗泽. 遗传算法和改进的BP网络杂交法在岩土工程中应用[J].地下空间,2001,21(3):178-182.

WANG Zhiliang, LI Xiaoyan, YIN Zongze. Application of Genetic and Improved BP Algorithms in geotechnical engineering[J]. Underground Space, 2001, 21(3): 178-182.

[9]HSU K L, GUPTA H V, SORROSHIAN S. Artificial Neural Network Modeling of the Rainfall-runoff Process[J]. Water Resources Research, 1995, 31(10): 2 517-2 530.

[10]罗戎蕾，刘绍华，苏晨. 基于遗传算法的BP神经网络服装销售预测方法[J].北京邮电大学学报，2014,37(4): 39-43.

LUO Ronglei, LIU Shaohua, SU Chen. Garment Sales Forecast Method Based on Genetic Algorithm and BP Neural Network[J]. Journal of Beijing University of Posts and Telecommunications，2014,37(4): 39-43.

[11]赵世麒, 席丁民. 黄土砂砾层中大断面隧道成洞技术[J].

施工技术, 2006, 35(2): 57-59.

ZHAO Shiqi, XI Dingmin. Technology of Digging Large Section Tunnel in Loess and Gravel Layers[J]. Construction Technology, 2006, 35(2): 57-59.

[12]孙韶峰. 古迹坪隧道进口浅埋黄土层进洞施工技术[J]. 现代隧道技术, 2012, 49(4): 45.

SUN Shaofeng. Construction Technique for Gujiping Tunnel Portal Section in Shallow-buried Loess[J]. Modern Tunneling Technology, 2012,49(4):45.

[13]李健. 大断面黄土隧道初支作用机理及变形控制技术研究[D]. 北京: 北京交通大学, 2012.

[14]赵占厂. 黄土公路隧道结构工程性状研究[D]. 西安:长安大学, 2004.

[15]付望锋. 多翼离心风机内部流场分析、参数优化及噪声预测[D]. 武汉:华中科技大学, 2012.

[16]刘瑞江, 张业旺, 闻崇炜, 等. 正交试验设计和分析方法研究[J]. 实验技术与管理, 2010, 27(9): 52-55.

LIU Ruijiang, ZHANG Yewang, WEN Chongwei, et al. Study on the Design and Analysis Methods of Orthogonal Experiment[J]. Experimental Technology and Management, 2010, 27(9): 52-55.

[17]徐金俊, 陈宗平, 余兴国, 等. 长龄期再生混凝土弹性模量及泊松比试验研究[J]. 混凝土, 2012(1): 15-17,23.

XU Jinjun, CHEN Zongping, YU Xingguo, et al. Experimental Study of Elastic Molulus and Poisson's Ratios of Long Age Recycled Aggregate Concrete[J]. Concrete, 2012(1): 15-17, 23.

[18]王元丰, 梁亚平. 高性能混凝土的弹性模量与泊松比[J].北方交通大学学报, 2004, 28(1): 5-7, 16.

WANG Yuanfeng, LIANG Yaping. Study on Modulus of Elasticity and Poisson Ratio of High Performance Concrete[J]. Journal of Northern Jiaotong University, 2004, 28(1): 5-7,16.

[19]韩桂武. 隧道施工过程的动态监测及反演分析研究[D].沈阳:东北大学, 2007.

[20]中华人民共和国铁道部. TB 10003—2005 铁路隧道设计规范[S].北京:中国铁道出版社，2005.

[21]中华人民共和国交通部.JTG D70—2004 公路隧道设计规范[S].北京:人民交通出版社，2004.