明挖卸荷对下卧地铁双洞隧道变形影响的计算方法研究

周泽林， 陈寿根， 张海生， 涂 鹏， 张 恒

(1. 西南交通大学 交通隧道工程教育部重点实验室，四川 成都 610031；2. 西南交通大学 土木工程学院，四川 成都 610031)

随着我国城市地下空间的大规模开发，越来越多的新建基坑工程将紧邻或位于既有地铁隧道上方，在这种情况下，上部开挖卸荷必然对地铁结构造成附加应力和变形，而已建地铁隧道对变形要求极为严格。因此，如何准确、有效地预测与评估基坑施工所引起的邻近地铁隧道变形是当前亟待解决的一个工程难题。

目前国内外学者在该问题上已进行了不少相关研究。数值模拟方面:Sharma[1]报道了新加坡某基坑施工对邻近隧道的影响实例，并采用数值模拟评估了邻近开挖对隧道的影响程度；黄宏伟[2]利用有限元软件PLAXIS研究了上海市某基坑开挖对下卧延安东路越江公路隧道引起的变形和内力，并对加固措施效果进行了评价；高广运[3]结合上海市某邻近地铁隧道的基坑工程，利用有限差分软件FLAC3D模拟了不同的基坑施工方案以及二次加固措施对已运营地铁隧道的变形影响；郑刚[4]、王卫东[5]和蒋洪胜[6]等学者亦采用数值模拟方法对类似工例进行了研究，但这些成果都是依托于某个具体工程实例而开展的分析，不能针对该类问题提出一个通用的简化计算方法，且数值模拟往往依赖大型专业软件，建模工作量大，参数确定较复杂。解析理论方面：陈郁[7]采用弹性理论和Winkler地基梁理论推导了基坑开挖引起的邻近隧道隆起变形的定量计算方法；张治国[8]考虑基坑侧壁应力释放的影响，运用弹性地基梁法提出了计算隧道纵向的附加位移与内力的两阶段法；张冬梅[9]、黄栩[10]和张桓[11]等基于两阶段法，采用改进后的地基梁模型分析了邻近开挖对既有隧道的影响，以提高计算精度。

两阶段解析法的有效性已在实践中得到了验证[8-11]，但目前的解析理论都是集中于对土体自由位移场条件下单洞隧道研究。实际上，城市地铁往往是双线并行，当净距较小时存在“双洞效应”，即分析一条隧道的变形时需考虑另外一条隧道的存在对其附加应力和变形的影响。因此，考虑到近接双洞隧道之间的相互影响，本文首先基于弹性力学Mindlin解和Pasternak地基梁理论来分析基坑开挖引起的隧道与土体之间的接触压力和变形，并推导“双洞效应”下隧道纵向附加应力和变形的表达式；然后对弹性空间法获取的计算参数进行修正，以提高计算精度；最后依托实际工程，将隧道变形的解析解分别与数值模拟和实测数据进行对比验证。

1 基坑卸荷对下卧双洞隧道影响的计算模型

1.1 计算模型及假定

图1给出了明挖基坑卸荷对下卧双洞隧道影响的模型示意图：以基坑中心点地面坐标为原点建立三维空间坐标系，基坑横向(x轴向)开挖宽度为B，纵向(y轴向)开挖长度为L，竖向(z轴向)开挖深度为H；下卧地铁双洞隧道中的左线(隧道1)轴线坐标为(x1,y,z1)、右线(隧道2)轴线坐标为(x2,y,z2)。

基坑开挖后会形成5个卸荷面(1个坑底面和4个侧壁面)，见图1，其中，坑底面编号为⓪；侧壁面编号为分别①、②、③、④。分析中假定：

(1) 基坑开挖时，下卧双洞隧道已经存在，且隧道轴线平行于基坑长边；

(2) 隧道与土体不发生分离，满足变形协调条件；

(3) 将土体视为均质线弹性半无限体。

1.2 基坑土体卸荷量计算

从图1可以看出，基坑开挖引起的土体卸荷可以分为两部分：一是坑底面土体竖向卸荷；二是侧壁面土体水平卸荷。

基坑开挖前，坑底土体受到竖直方向大小为γH(γ为开挖土层的容重加权值)矩形分布荷载，侧壁上土体受到水平方向大小为K0γz(K0为静止土压力系数)的三角形分布荷载。因此，开挖后坑底土体竖向卸荷相当于对基坑底面反方向施加大小为γH的荷载。

确定开挖后四周侧壁面土体水平卸荷时，由于围护结构的存在，需考虑 “围护结构-土体”之间的相互作用。根据增量法计算土压力的思想[12]，作用在围护结构上的土压力为开挖前到开挖完成后的土压力增量，该土压力增量正是主动区土体卸荷产生的不平衡力，即水平卸荷量。

开挖前，围护墙体前、后的土压力均为静止土压力，大小为K0γz；开挖后，墙后土体形成主动土压力区，假定桩后填土表面水平，桩背垂直光滑，不考虑桩身变形的影响，且主动区土体达到极限平衡状态，见图2。根据郎肯土压力理论，主动土压力Q1大小为

( 1 )

如图2中阴影部分所示，开挖后墙后土压力减少了一个三角形区域bce(砂性土中)或四边形区域bcde(黏性土中)，该减小值即为水平卸荷量。因此，侧壁上的土体水平卸荷相当于对侧壁面反方向施加大小为K0γz-Q1的水平荷载。

2 开挖对下卧单洞隧道的影响

2.1 单洞隧道附加应力

首先分析基坑下方只有一条隧道的情况，见图3。基坑开挖卸载对下卧地基中的隧道造成竖向附加应力σz(y)，隧道在该竖向附加应力下发生回弹上浮变形。

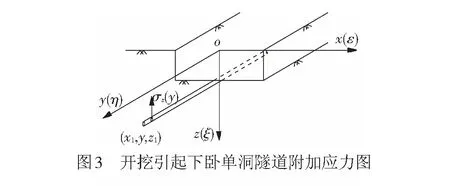
其中， 坑底面土体竖向卸载作用可以划分为无数个微小单元上单位竖向力γHdεdη的作用之和。根据弹性力学Mindlin基本解，采用积分的方法可得出整个坑底面竖向卸载引起的隧道轴线上任意一点(x1,y,z1)处的竖向附加应力σz0(y)为

σz0(y)=

( 2 )

式中：z1=z-H、z2=z+H、z3=5z-H；u为弹性土体泊松比

u1=(1-2u)/(1-u)

u2=(3-4u)/(1-u)

u3=1/(1-u)

Γ0为基坑开挖深度z=H处整个坑底面所对应的积分区域，取值范围为z=-H，-B/2≤ε≤B/2，-L/2≤η≤L/2。

同理，编号为①的侧壁面土体水平卸载作用可以划分成无数个微小单元上的单位水平力(K0γz-Q1)dηdξ的作用之和。根据Mindlin基本解，编号为①侧壁面水平卸载在隧道轴线上任意一点(x1,y,z1)处引起的竖向附加应力σz1(y)为

( 3 )

式中：Γ1是编号为①的基坑侧壁面对应的积分区域，深度z从地表z=0面取至坑底z=H,取值范围x=-B/2，-L/2≤y≤L/2，0≤z≤H。

类似于σz1(y)的推导过程，可分别求出编号为②、③和④的侧壁面土体水平卸载在隧道轴线上引起的竖向附加应力σz2(y)、σz3(y)和σz4(y)。所涉及的积分运算可通过Gauss-legendre数值积分方法进行求解。根据叠加原理，整个基坑开挖卸载引起的作用于隧道轴线上任意一点(x1,y,z1)处的竖向附加应力为

( 4 )

2.2 单洞隧道纵向变形

分析隧道在竖向附加应力作用下的纵向变形时，将隧道视为一根欧拉伯努利长梁，纵向等效刚度为EI(考虑到地铁隧道管片接缝存在对纵向刚度的减弱，计算EI的大小时引入纵向刚度折减率)，并采用Pasternak弹性地基梁模拟隧道变形。

(1) 隧道平衡微分方程

Pasternak地基模型[13]是在传统的Winkler地基模型上加入一个剪切层(剪切刚度为Gp)，使得弹簧单元之间产生联系，能反映地基应力和变形的扩散性，从而使计算结果更加合理，见图4。采用Pasternak地基梁模拟“隧道-土体”接触变形时，竖向接触压力F(y)由两部分构成：一部分是开挖引起的作用于隧道的竖向荷载-p1(y)；另一部分是地基梁的土弹簧单元和剪切单元给与的外荷载p2(y)，即

F(y)=-p1(y)+p2(y)

( 5 )

p1(y)=D·σz(y)

( 6 )

( 7 )

式中：D为管片外径；Kp为地基基床系数；w(y)为隧道竖向附加位移；s(y)为土弹簧单元竖向位移，由于隧道和土体不发生分离，有s(y)=w(y)。

根据材料力学中微段梁的受力平衡和变形协调原理，可得出隧道的纵向力学平衡微分方程为

( 8 )

(2) 微分方程的解

式( 8 )是一个四阶非齐次常微分方程，令方程等式右边常数项为0，得到式( 8 )对应的四阶齐次常微分方程

( 9 )

齐次常微分方程( 9 )的特征方程为

(10)

常微分方程( 9 )的通解形式取决于特征方程(10)的判别式

Δ=[(DGp)2-4DKp]/(EI)2

利用微分方程的求解方法，并考虑到y→∞时，w(y)=0，可得出式( 9 )的通解为

(11)

式中：α、β为与隧道纵向等效刚度EI、直径D以及地基参数Kp、Gp有关的量；判别式Δ的物理意义表示实际隧道与周围土体的刚度比：Δ>0表示隧道刚度大于周围土体刚度；Δ≤0表示隧道刚度小于或等于周围土体刚度，这种情况在现实中不存在。因此，微分方程( 9 )的通解实际上只有一种形式，即w(y)=A1e-αx+A2e-βx。

假设隧道轴线上某一点y=η上受到单位集中荷载q(η)dη的作用，荷载作用点存在以下边界条件

(12)

根据以上边界条件可以求得隧道在单位集中荷载作用下任意一点的位移特解为

(βe-αy-η-αe-βy-η)dη

(13)

对式(13)在隧道纵向附加荷载分布范围内积分，即可得出开挖引起的隧道纵向上浮变形

(14)

进一步，可得出开挖引起的隧道纵向弯矩和剪力

(15)

3 开挖对下卧双洞隧道的影响分析

当基坑下方存在两条近接隧道时，两条隧道之间存在“双洞效应”。此时，分析任一条隧道上的竖向附加应力的过程中，需要考虑另外一条隧道的存在对其附加应力的影响。

3.1 “双洞效应”下隧道的附加应力

图5表示基坑下方存在两条近接隧道时，基坑开挖在其中任意一条隧道(如隧道1)上造成的竖向附加应力示意图。

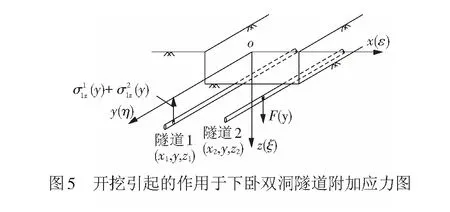
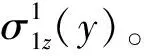
考虑隧道2的存在对隧道1附加应力的影响，由于隧道2与土体之间存在接触压力，根据力的相互作用原理，隧道2会对周围土体施加一个大小相同、方向相反的接触压力。根据Mindlin基本解，采用积分的方法可以求出隧道2与土体间接触压力在隧道1轴线上形成的附加应力

(16)

式中：F(y)是隧道2与土体之间的接触压力，可根据式( 5 )～式( 7 )求出；Lm为沿隧道2轴向(y轴)的积分范围，一般情况下，基坑开挖荷载的纵向影响范围为-6L～6L[14]，为了使计算结果更准确，本文取值为Lm=10L；

(17)

同理，在分析隧道2的竖向附加应力时，亦考虑隧道1在抵抗地层变形过程中所形成的接触压力的影响。分别求出两条隧道的竖向附加应力之后，采用上节Pasternak弹性地基梁法，即可求出双洞隧道的纵向变形大小与分布，限于篇幅，不再展开。

3.2 双洞隧道附加应力的算例验证

假设某基坑平面开挖尺寸L×B=28 m×32 m、开挖深度H=8.0 m；下卧双洞隧道轴线平行于基坑长边，隧道1和隧道2埋深分别为21.0 m和18.0 m，隧道轴线坐标分别为(x1,y,z1)=(-16,y,21)、(x2,y,z2)=(-3,y,18)，纵向刚度为EI=7.54×1011N·m2；场地为均质土体，土体弹性模量E=89.1 MPa、泊松比u=0.3、重度γ=1 810.0 kN/m3、侧压力系数K0=1.0、Ka=0.6。算例采用有限差分数值模拟方法借助岩土专业软件FLAC3D进行验证。数值模拟中为与本文理论模型的假定条件保持一致，使数值解和解析解具有可比性，数值建模时采用线弹性模型模拟土体变形，采用梁单元模拟隧道，并假定隧道与土体不发生分离。

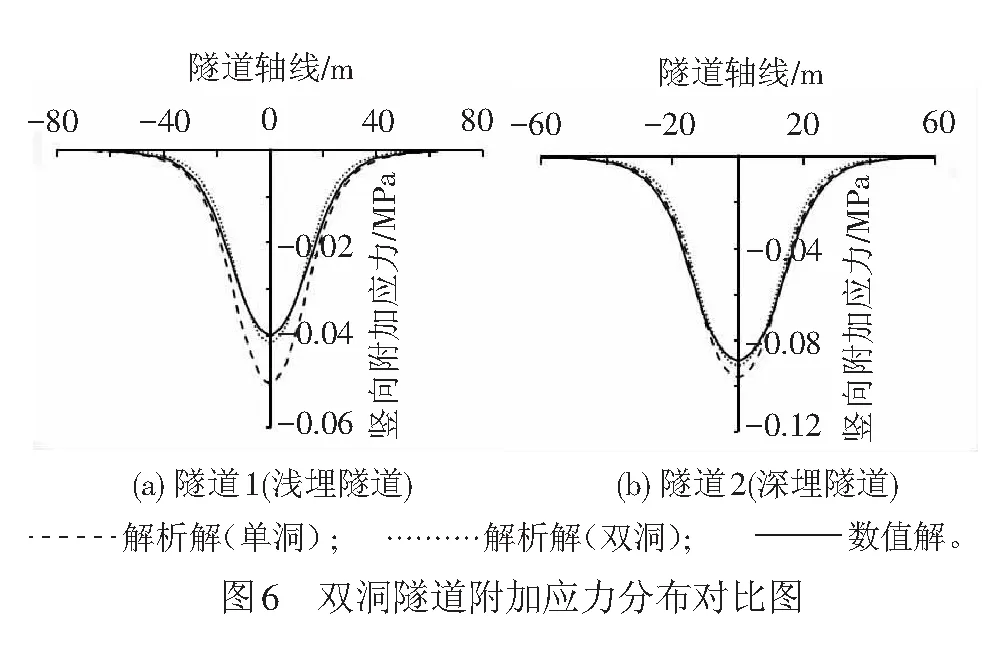
图6给出了双洞隧道竖向附加应力分布对比图，其中，解析解(单洞)曲线表示不考虑隧道之间相互影响的附加应力，解析解(双洞)表示考虑“双洞效应”作用的隧道附加应力。从图6可见，如果不考虑 “双洞效应”，附加应力最大值分别为0.051 MPa(隧道1)、0.096 MPa(隧道2)；考虑“双洞效应”时，附加应力最大值分别为0.041 MPa(隧道1)、0.091 MPa(隧道2)，与单洞情况相比分别减少了21.2%、5.4%。说明两近接隧道之间发生了较明显的相互影响，主要表现为一条隧道的刚度在发生抵抗地层变形的过程中减小另外一条隧道所承受的地层附加应力，且隧道1(浅埋隧道)对隧道2(深埋隧道)的影响程度更大；考虑“双洞效应”情况得出的隧道附加应力解析解和数值模拟结果能较好地吻合，验证了本文方法的合理性。

4 大型工程实例应用

为了验证本文方法的有效性，依托某近接已建小净距地铁双洞隧道的明挖隧道工程实例开展方法运用与分析。其中，上方新建公路隧道为矩形断面，以U型槽和闭合框架为主，施工采用分段明挖顺做法，研究区段平面开挖尺寸L×B=40 m×36 m，开挖深度H=8.1 m。下卧地铁双洞隧道之间的水平中心间距为9.7 m，左线与基坑中心水平间距为17.9 m，埋深14 m。新建公路隧道与已建地铁隧道之间形成了三孔差异断面近接隧道重叠并行的特殊工况，见图7。

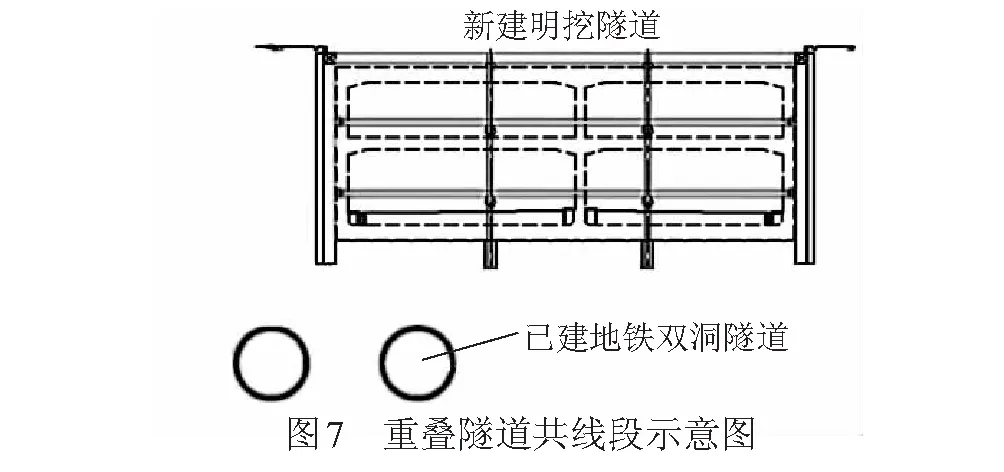
场地以人工填土层和砾质黏性土层为主，根据地勘资料，取土层弹性模量加权值E=26.9 MPa，泊松比u=0.3，土层重度加权值γ=1 826.0 kN/m3。盾构隧道管片外径D=6.0 m，壁厚0.35 m，混凝土弹性模量Ec=34.5 GPa，纵向刚度有效率为1/6。

由于隧道重叠段距离长，且存在小净距、浅覆土施工等极端工况，上部大范围明挖卸荷必然会诱发下部已建地铁双洞隧道上浮变形，给工程带来安全隐患。因此，如何预测施工过程中地铁隧道纵向上浮变形是一个工程难点。结合实际工程，研究中分别采用理论方法、数值模拟方法和现场监测方法，对下卧地铁双洞隧道纵向变形大小、曲率和弯矩等进行对比分析。

4.1 理论分析中基本参数的修正

采用弹性地基梁模型分析隧道变形时，一个很重要的问题是如何确定地基参数Gp和Kp的取值。本文引用从弹性连续体方程中推导出的地基参数，即简化弹性空间法[15-16]：对于一个弹性模量为E，泊松比为u，厚度为h的地基，Pasternak地基模型参数为

(19)

式中:Gs为土体剪切刚度；h为隧道下方的地基厚度，是指隧道底部土体受附加应力的影响深度范围，根据徐凌[14]的研究，对于隧道、管线这类条形状基础，当下方地基土体深宽比大于6时，基底附加应力已衰减的非常小而可以忽略。因此，根据经验h可近似取为h=6D。

从式(19)可知，采用弹性空间法确定地基参数时，基本计算参数只有三个：E、u和h。本节利用3.2节算例对这三个基本计算参数进行了单因素敏感性分析，结果见图8。可见，弹性模量E和地基厚度h对变形的影响很大，表现为E的取值越大，隧道上浮变形越小，但变形减小的梯度逐渐变缓；h取值越大，隧道上浮变形越大，但变形增大的梯度逐渐变缓；泊松比u取值变化却对隧道变形基本上不产生影响。

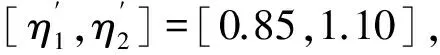
4.2 数值模拟

算例借助有限差分软件FLAC3D进行了验证，图10为三维数值模型图。

为使数值解和解析解的计算结论具有可比性，数值建模中将地层视为等效均质土体(土体参数取各地层参数的加权平均值)，采用线弹性本构模型模拟土体；采用梁单元模拟支护排桩；采用壳单元来模拟隧道，并假定隧道与土体不发生分离，使数值模拟与理论方法中的假定条件和计算模式基本保持一致。土体、管片和支护结构等材料参数的取值见表1～表3。其中，管片纵向弯曲刚度有效率为1/6,支护排桩界面面积为0.78 m2。

表1 地层计算参数

表2 管片计算参数

表3 围护墙(支护排桩)计算参数

4.3 计算结果对比与分析

(1) 纵向上浮变形

基坑施工时，对下卧地铁隧道变形进行了监测，图11为隧道纵向上浮变形的解析解、数值解以及现场监测数据对比图。可见，最大上浮变形出现在基坑中心下方，且右线的上浮变形比左线大，表明距开挖卸荷范围越近，隧道受扰动程度越大；纵向距基坑中心100 m处的附加变形趋近于0，开挖在纵向对隧道的影响范围约为5倍开挖长度。

隧道变形的解析解与监测数据相比，两者的大小和分布形状基本吻合，最大变形偏差率为4.4%(左线)、2.5%(右线)，计算精度能满足工程要求。与数值解相比，两者有良好的一致性，验证了本文方法的合理性，亦表明通过简单工况经解析试算得出的修正地基参数可以较准确地用于预测和分析实际复杂工况条件下的隧道变形。

(2) 纵向变形曲率

图12表示左线隧道纵向变形曲率的解析解和数值解对比图。与数值解相比，纵向最大曲率偏差率为7.1%。其中，曲率为0的点代表了隧道纵向变形的反弯点，反弯点位置出现在距离基坑中心100 m附近，即2.5倍开挖长度。最大曲率值的Pasternak解析解为0.059‰，出现在距基坑中心30 m附近的位置，对应的曲率半径为16 949 m；根据《上海市地铁沿线建筑施工保护地铁技术管理暂行规定》[17]：地铁隧道受邻近施工影响时，变形曲率半径不得小于15 000 m。表明本隧道变形的计算结果满足地铁保护要求。

(3) 纵向弯矩

图13表示左线隧道左线纵向弯矩的解析解和数值解对比图。隧道纵向最大弯矩值的解析解为1.23 MN·m，与数值解相比偏差率为11.6%。最大正弯矩位于基坑中心正下方，该断面拱顶处管片接缝螺栓处于受拉的最不利状态；最大负弯矩出现在距离基坑中心约40 m的位置，该断面拱底处管片接缝螺栓处于受拉的不利状态；距离基坑中心约20 m处(即纵向侧壁开挖面)的纵向弯矩为0，根据材料力学可知，弯矩为0的断面上对应的剪力值最大，表明该断面管片接缝螺栓处于受剪最不利状态。施工中应当加强以上三个不利断面的变形监测，以将不利影响降至最低。

5 结论

(1) 基于Mindlin基本解建立明挖基坑施工引起的土体附加应力的计算模型时，不仅考虑了坑底和四周侧壁面上土体的卸荷效应，同时考虑了侧壁处“围护结构-土体”之间相互作用对附加应力的影响，因而更接近实际情况；

(2) 与单洞隧道情况相比，邻近开挖引起双洞隧道附加应力的计算值偏小，这是由于近接双洞隧道的存在相当于在整体上增强了地层的刚度，且两隧道之间的受力发生相互影响，计算中应考虑这种“双洞效应”的作用；

(3) 通过建立简单工况模型并采用解析试算的方法对弹性空间法获取的地基参数进行修正之后，再将修正后的地基参数用于同一地层条件下实际复杂工况的隧道变形分析，可以提高计算精度，获得较准确的计算结果；

(4) 采用提出方法计算得出的隧道纵向变形、曲率和弯矩的大小和分布规律都与数值解都具有良好的一致性，且隧道变形的解析解与实测变形数据基本吻合，验证了方法的合理性。

本文提出的方法作为一种针对基坑开挖对邻近隧道变形影响的近似解，对一般基坑工程，变形的定量分析结果是可接受的，但对于内支撑布置较多的深大复杂基坑，则不推荐使用本文方法进行定量分析，仅作为定性分析。

参考文献：

[1] SHARMA J S, HEFNY A M. Effective of Large Excavation on Deformation of Adjacent MRT Tunnel[J]. Tunneling and Underground Space Technology, 1972(7):11-23.

[2] 黄宏伟, 黄栩, HELMUT Schweiger F. 基坑开挖对下卧运营盾构隧道影响的数值模拟研究[J]. 土木工程学报, 2012, 45(3): 182-189.

HUANG Hongwei, HUANG Xu, HELMUT Schweiger F. Numerical Analysis of the Influence of Deep Excavation on Underneath Road Tunnel[J]. China Civil Engineering Journal, 2012, 45(3): 182-189.

[3] 高广运, 高盟, 杨成斌, 等. 基坑施工对运营地铁隧道的变形影响及控制研究[J]. 岩土工程学报, 2010, 32(3): 453-459.

GAO Guangyun, GAO Meng, YANG Chenbin, et al. Influence of Deep Excavation on Deformation of Operating Metro Tunnels and Countermeasures[J]. Chinese Journal of Geotechnical Engineering, 2010, 32(3): 453-459.

[4] 郑刚, 刘庆晨, 邓旭. 基坑开挖对下卧运营地铁隧道影响的数值分析与变形控制研究[J]. 岩土力学, 2013, 34(5): 1 459-1 468.

ZHENG Gang, LIU Qingchen, DENG Xu. Numerical Analysis of Effect of Excavation on Underlying Existing Metro Tunnel and Deformation Control[J]. Rock and Soil Mechanics, 2013, 34(5): 1 459-1 468.

[5] 王卫东, 吴江斌, 翁其平. 基坑开挖卸载对地铁区间隧道影响的数值模拟[J]. 岩土力学, 2004, 25(S2): 251-255.

WANG Weidong, WU Jiangbin, WENG Qiping. Numerical Modeling of Affection of Foundation Pit Excavation on Metro Tunnel[J]. Rock and Soil Mechanics, 2004, 25(S2): 251-255.

[6] 蒋洪胜, 侯学渊. 基坑开挖对临近软土地铁隧道的影响[J]. 工业建筑, 2002(5): 53-56.

JIANG Hongsheng, HOU Xuyuan. The Influence of Deep Excavation on Adjacent Metro Tunnel in Soft Ground[J]. Industrial Building, 2002(5): 53-56.

[7] 陈郁, 李永盛. 基坑开挖卸荷引起下卧隧道隆起的计算方法[J]. 地下空间与工程学报, 2005, 1(1): 92-94.

CHEN Yu, LI Yongsheng. Calculation of Tunnel Heaving due to Unloading of Pit Excavation[J]. Chinese Journal of Underground Space and Engineering, 2005, 1(1): 92-94.

[8] 张治国, 黄茂松, 王卫东. 邻近开挖对既有软土隧道的影响[J]. 岩土力学, 2009, 30(5): 1 373-1 380.

ZHANG Zhiguo, HUANG Maosong, WANG Weidong. Responses of Existing Tunnels Induced by Adjacent Excavation in Soft Soils[J]. Rock and Soil Mechanics, 2009, 30(5): 1 373-1 380.

[9] 张冬梅, 宗翔, 黄宏伟. 盾构隧道掘进引起上方已建隧道的纵向变形研究[J]. 岩土力学, 2014, 35(9): 2 659-2 666.

ZHANG Dongmei, ZONG Xiang, HUANG Hongwei. Longitudinal Deformation of Existing Tunnel due to Underlying Shield Tunneling[J]. Rock and Soil Mechanics, 2014, 35(9): 2 659-2 666.

[10] 黄栩, 黄宏伟, 张冬梅. 开挖卸荷引起下卧已建盾构隧道的纵向变形研究[J]. 岩土工程学报, 2012, 34(7): 1 241-1 249.

HUANG Xu, HUANG Hongwei, ZHANG Dongmei. Longitudinal Deflection of Existing Shield Tunnels due to Deep Excavation[J]. Chinese Journal of Geotechnical Engineering, 2012, 34(7): 1 241-1 249.

[11] 张桓, 张子新. 盾构隧道开挖引起既有管线的竖向变形[J]. 同济大学学报:自然科学版, 2013, 41(8): 1 172-1 178.

ZHANG Huan, ZHANG Zixin. Vertical Deflection of Existing Pipeline due to Shield Tunneling[J]. Journal of Tongji University: Natural Science, 2013, 41(8): 1 172-1 178.

[12] 杨光华. 深基坑支护结构的实用计算方法及其应用[M]. 北京: 地质出版社, 2004: 104-108.

[13] PASTERNAK P L. On a New Method of Analysis of an Elastic Foundation by Means of Two-constants[M]. Moscow: State Architecture & Construction Press, 1954.

[14] 徐凌. 软土盾构隧道纵向沉降研究[D]. 上海: 同济大学, 2005.

[15] MORFIDIS K. Research and Development of Methods for the Modeling of Foundation Structural Elements and Soil[D]. Thessaloniki: Aristotle University of Thessaloniki, 2003.

[16] KERR A D. On the Determination of Foundation Model Parameters[J]. Journal of Geotechnical Engineering, 1985, 111(11): 1 334-1 340.

[17] 上海市市政工程管理局. 沪市政法[94]第854号 上海市地铁沿线建筑施工保护地铁技术管理暂行规定[Z].上海：上海市市政工程管理局，1994.