无绝缘轨道电路可靠度的计算

陈 琛， 赵林海,2

(1. 北京交通大学 电子信息工程学院，北京 100044； 2. 北京交通大学 轨道交通控制与安全国家重点实验室，北京 100044)

无绝缘轨道电路(JTC)作为铁路列车运行控制系统的重要组成部分，其可靠性的高低直接关系到行车安全、运输与维护效率等多个方面，因此一个准确的JTC可靠度计算方法对于列控系统至关重要。

目前国内外对JTC可靠性已经开展了相应的研究。其中，针对JTC的发送器和接收器研究包括：Dobias等采用马尔可夫过程分析了捷克国内所使用的基于“3选2”原则的JTC接收器的可靠性[1]。Antoni基于法国铁路情况，采用威布尔分布分析了发送器的寿命分布及环境因素对退化过程的影响[2]。在国内，陈建明等采用马尔可夫过程分析了发送器在“N+1”热备方式下的可靠性[3]。陈永刚等采用马尔可夫过程分别分析了“N+1”热备发送器和双机热备接收器的可靠性[4]。符萌采用相似产品法和元件计数法对发送器和接收器进行了可靠性预计[5]。关琼基于马尔可夫过程，分析了发送器采用不同热备方式，即“1+1”热备和“N+1”热备对ZPW-2000JTC可靠性的影响[6]。米根锁通过收集历史失效数据，计算了发送器和接收器的平均剩余寿命并进行可靠性分析[7]。

在系统可靠性层面，徐敏对UM71JTC进行了故障模式及影响分析，并计算了相应的可靠性指标[8]。王文斌等对JTC分别进行了故障模式及影响分析和故障树分析[9-10]。苏宏升等研究了ZPW-2000JTC的可靠性、可用性和维修性[11]。张菊等利用故障树分析方法和事件树分析方法分析了JTC的安全性[12]。在此，需要指出，文献[8-11]在定量分析JTC的可靠性时，普遍将补偿电容等效为串联可靠性关系，即认为只要有补偿电容故障会导致JTC系统失效。但由现场调研可知，正常情况下单个补偿电容故障往往不会使JTC系统失效，即其接收器接收信号振幅不会低于相应的接收门限。图1为相应微机监测设备所提供的2007年10月某个JTC接收器输入信号电压的某月变化情况，且该JTC中的补偿电容C4在22日发生断线，在24日被更换。从图1中可以看出，C4发生断线故障使接收器信号振幅下降，但并没有低于接收器的接收阈值，即该JTC在C4断线时仍能正常工作。

可见JTC系统中补偿电容在可靠性层面存在冗余设计。若按文献[8-11]把补偿电容等效为串联可靠性关系则不能真实地反映补偿电容间的这种冗余设计，其相应的分析结果也不能真实地反映JTC的实际可靠性情况。因此，需要基于补偿电容的这种冗余设计计算JTC可靠度，以满足目前高铁发展的需求。

本文基于JTC信号传输模型，通过仿真计算所有补偿电容正常与故障状态下JTC接收信号的振幅，并以此建立补偿电容与轨道线路之间的状态真值表；然后利用真值表计算出了轨道线路可靠度；最后基于所得到的轨道线路可靠度，计算了JTC可靠度。

1 JTC系统构成及接收器输入信号的建模

1.1 JTC的系统构成

JTC的系统构成见图2，JTC主要由发送器、发送电缆、发送端匹配变压器、发送端调谐区、带有补偿电容的轨道线路、接收端调谐区、接收端匹配变压器、接收电缆和接收器组成。

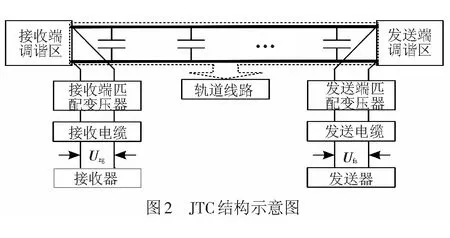
1.2JTC接收器输入信号Uzg的建模

根据传输线理论，JTC除发送器和接收器外的其他部分由相应的传输特性等效四端网络描述。

(1) 轨道线路传输特性等效四端网络Ngd

设JTC轨道线路除两端调谐区之外长度为lgd，补偿电容个数为m，则轨道线路可划分为m个补偿单元级联的形式。其中，补偿单元见图3，其长度lut可表示为lut=lgd/m，由一个补偿电容Ccp以及电容两端长度同为lut/2的钢轨线路构成。

其中，Ngglut/2和Ncp分别为半个补偿单元长度钢轨和补偿电容的传输特性等效四端网络。设γg和zcg为钢轨的传输常数和特性阻抗，Zcp为补偿电容容抗，则Ngglut/2和Ncp可分别表示为

( 1 )

( 2 )

根据传输线理论[13]，补偿单元的传输特性等效四端网络为

Nut=Ngglut/2×Ncp×Ngglut/2

( 3 )

考虑到轨道线路为m个补偿单元级联，故Ngd可表示为

Ngd=Nutm

( 4 )

(2) 调整状态下JTC信号传输特性等效四端网络Nsr

设接收和发送电缆的传输特性等效四端网络分别为Nre和Nse，接收和发送端匹配变压器的传输特性等效四端网络分别为Nrm和Nsm，接收和发送端调谐区的传输特性等效四端网络分别为Nrp和Nsp，且由式( 1 )～式( 4 )，JTC由发送器到接收器的传输特性等效四端网络Nsr可表示为

Nse×Nsm×Nsp×Ngd×Nrp×Nrm×Nre

( 5 )

(3)Uzg及其振幅Azg的建模

设接收器输入电流信号为Izg，接收器的输入阻抗为Zzg，则Uzg和Izg满足关系

Izg=Uzg/Zzg

( 6 )

由传输线理论可得，Ufs与Uzg和Izg之间满足关系

Ufs=Nsr11×Uzg+Nsr12×Izg

( 7 )

由式( 6 )、式( 7 )，Uzg可表示为

( 8 )

设Afs为Ufs的振幅，·为复数取模运算符，则由式( 8 )，Azg可表示为

( 9 )

2 补偿电容故障的影响分析

3 JTC可靠度计算

考虑到补偿电容组合故障对JTC接收器输入信号的影响较为复杂，故在此采用直接枚举法计算轨道线路可靠度，并假设除轨道线路外，JTC其他组成部分的可靠度为已知且保持不变，则相应的可靠度计算流程见图5，主要分为基于仿真的轨道线路可靠性真值表构造、轨道线路可靠度计算和JTC可靠度计算等3部分。

(10)

式中:Si为第i种补偿电容组合状态Di所对应的轨道线路状态，其为0表示轨道线路正常，而为1则对应轨道线路失效。最终，基于式(10)可得到补偿电容状态Di与轨道线路状态Si的对应关系，并以此建立相应的真值表。

在轨道线路可靠度计算环节，已知单个补偿电容的失效率为λcp，且其失效分布是指数分布[8]，故Rcp(t)可表示为

Rcpt=e-λcpt

(11)

基于以上所得到的真值表和式(11)，分别计算其中使轨道线路能够保持工作的各状态DiSi=0所对应的可靠度

Ri(t)D(i)|S(i)=0=

(12)

式中：mpi为DiSi=0中正常电容个数。因此，轨道线路可靠度可表示为

Rget=∑RitDiSi=0

(13)

在JTC可靠度计算环节，已知JTC其他组成部分服从指数失效分布[10]，且其失效率保持不变，则有JTC系统发送器、传输电缆、匹配变压器、调谐单元和接收器的失效率分别为λtr、λca、λmt、λta和λre。因此，除轨道线路外，JTC其他组成部分的可靠度可分别表示为

Rtrt=e-λtrtRcat=e-λcatRmtt=e-λmtt

Rtat=e-λtatRret=e-λret

(14)

则JTC系统可靠度可表示为

RJEt=Rtrt·Rcat·Rmtt·Rtat·

Rgdt·Rtat·Rmtt·Rcat·Rret

(15)

4 算例分析与算法对比

4.1 算例分析

这里，按照图4的仿真条件，根据图5计算该JTC的可靠度RJEt。

表1 基于图4仿真条件的轨道线路可靠性真值表

继而，在轨道线路可靠度计算环节，已知单个补偿电容的失效率λcp=1.8×10-6/h[10]，由式(11)可计算得到单个补偿电容的可靠度为

Rcpt=e-1.8×10-6t

(16)

针对以上所得到的真值表，可利用式(12)分别计算相应的RitDiSi=0，见表2。

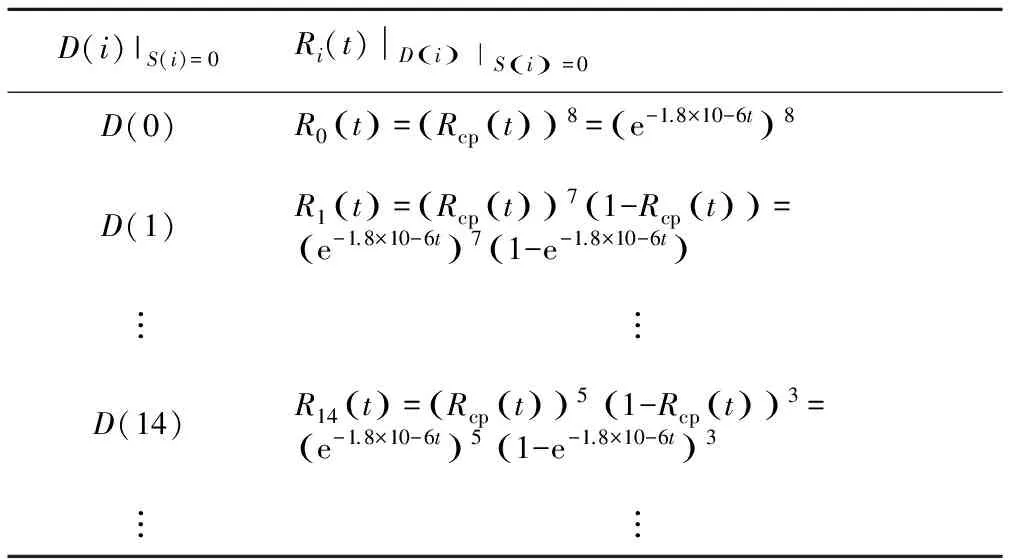
表2 各状态DiSi=0所对应的可靠度RitDiSi=0

基于式(13)对表2中各项求和，该JTC轨道线路Rget将表示为

Rget=Rcpt8+Rcpt71-Rcpt+

…+Rcpt51-Rcpt3+…

(17)

由式(17)，计算得到该JTC轨道线路可靠度Rge(t)见图6中实线。

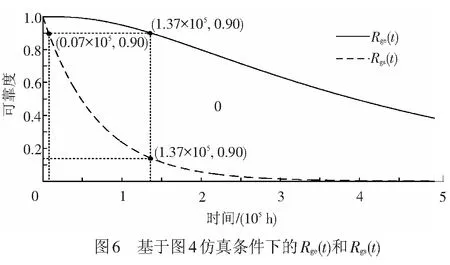
最后，在JTC可靠度计算环节，根据文献[10]，JTC各组成部分失效率的值，见表3。

表3 JTC各组成部分的失效率

基于式(14)、式(15)，得到相应的RJEt，见图7中实线。

4.2 算法对比

在此，将本文计算结果与参考文献[8-11]中将各补偿电容直接等效为串联可靠性模型的情况进行对比。其中，在相同仿真条件下，基于补偿电容直接串联模型的轨道线路可靠度可表示为

Rgst=Rcpt8=e-8λcpt

(18)

其计算结果如图6中虚线所示。基于这一计算结果，再由式(14)、式(15)进一步计算出电容直接串联模型的JTC可靠度RJst，见图7中虚线。

比较图6中的Rget和Rgst可见，Rge(t)和Rgs(t)仅在总体变化趋势上基本相同，而在随时间的下降程度上存在明显差异。由于本文算法考虑了补偿电容的可靠性冗余，Rget随时间的下降程度明显要慢于没有考虑相应冗余的计算结果Rgst，且这种差异会随着时间的延长而增大。例如，同样是可靠度下降到0.90，本文方法Rget所对应的时间为t=1.37×105h，而Rgst的时间仅为t=0.0732×105h，两者相差近20倍，而对于同一时间t=1.37×105h，Rget=0.9而Rgst仅为0.14。同样的变化规律也体现在图7中。例如，当可靠度下降到0.90时，本文方法RJEt所对应的时间为t=1.10×104h，而相应的RJSt的时间仅为t=0.45×104h，仅仅大致相当于RJEt的一半。

由此可见，补偿电容的可靠性冗余设计对于整个JTC至关重要。忽视这一冗余去计算JTC可靠度将会产生较大的误差。

5 结论

本文由铁路现场的实际运用数据发现JTC中的补偿电容采用了可靠性冗余设计，这与现有各文献普遍将其按串联可靠性模型来计算JTC可靠度相矛盾。为此，本文基于传输线理论，对调整状态下JTC接收器输入信号的振幅进行了建模，并以此模型遍历计算了各补偿电容不同状态下的信号振幅及其所对应的轨道线路状态，进而构造了相应的轨道线路可靠性真值表，依次计算出轨道线路和整个JTC的可靠度，并与原有文献中串联可靠性模型下的JTC可靠度相比较。结果表明，JTC中补偿电容的可靠性冗余设计对于JTC可靠度起着非常重要的作用。因此，本文所提出的考虑了补偿电容可靠性冗余的JTC可靠度的估计方法，能够更真实地反映JTC的实际可靠性状况，有利于现场维修策略的制定和优化。

参考文献：

[1] DOBIAS R, KONARSKI J, KUBATOVA H. Dependability Evaluation of Real Railway Interlocking Device[C]//Proceedings of 11thEUROMICRO Conference on Digital System Design Architectures, Methods and Tools(DSD '08).New York:IEEE, 2008: 228-233.

[2] ANTONI M. The Ageing of Signaling Equipment and the Impact on Maintenance Strategy[C]// Proceedings of International Conference on Computers & Industrial Engineering.Vienna：CIE, 2009:1 179-1 184.

[3] 陈建明, 何春明, 张仲义. 无绝缘区间设备系统可靠性分析[J]. 铁道学报, 1999, 21(5): 112-114.

CHEN Jianming, HE Chunming, ZHANG Zhongyi. System Reliability Analysis of Jointless Train Section Signal Facilities[J].Journal of the China Railway Society, 1999, 21(5): 112-114.

[4] 陈永刚, 王晓明, 林俊亭, 等. ZPW-2000A移频自动闭塞设备可靠性分析[J]. 兰州交通大学学报, 2005, 24(1): 26-28.

CHEN Yonggang, WANG Xiaoming, LIN Junting, et al. Reliability Analysis of Facilities for ZPW-2000A Shifting Frequency Automatic Blocking[J]. Journal of Lanzhou Jiaotong University, 2005, 24(1): 26-28.

[5] 符萌. ZPW-2000A中发送器和接收器的可靠性评估和可靠性试验设计[D].成都: 西南交通大学, 2010.

[6] 关琼. 客运专线ZPW-2000一体化轨道电路可靠性分析[J]. 铁道运营技术, 2014, 20(1): 58-60.

GUAN Qiong. Reliability Analysis of ZPW-2000 Integrated Track Circuit in Passenger Dedicated Line[J]. Railway Operation Technology, 2014, 20(1): 58-60.

[7] 米根锁, 张凤霞, 魏蕾. 基于剩余寿命的铁路轨道电路调整型维修方法研究[J]. 铁道学报, 2015, 37(4): 69-74.

MI Gensuo, ZHANG Fengxia, WEI Lei. Research on Method of Modulation Maintenance in Railway Track Circuit Based on Residual Life[J].Journal of the China Railway Society, 2015, 37(4): 69-74.

[8] 徐敏. UM71型JTC可靠性的研究[D]. 北京: 北京交通大学, 1999.

[9] 王文斌, 苏宏升. ZPW-2000A轨道电路系统的FMEA分析研究[J]. 兰州交通大学学报, 2014, 33(3): 146-149.

WANG Wenbin, SU Hongsheng. Analysis and Research on FMEA in ZPW-2000A Track Circuit System[J]. Journal of Lanzhou Jiaotong University, 2014, 33(3): 146-149.

[10] 王文斌, 苏宏升. 基于FMEA和FTA的ZPW-2000A轨道电路可靠性分析[J]. 计算机工程与应用, 2013, 49(21): 245-249.

WANG Wenbin, SU Hongsheng. Analysis on Reliability of ZPW-2000A Track Circuit Based on FMEA and FTA[J]. Computer Engineering and Application, 2013, 49(21): 245-249.

[11] 苏宏升, 王文斌. ZPW-2000A无绝缘移频轨道电路的RAM评估研究[J]. 铁道标准设计, 2013(7):111-114.

SU Hongsheng, WANG Wenbin. Evaluation Research on the RAM of ZPW-2000A Jointless Audio Frequency-shift Modulated Track Circuit[J]. Railway Standard Design, 2013(7):111-114.

[12] ZHANG Ju, ZHAO Huibing, ZHOU Guo, et al.. Safety Analysis of ZPW-2000A/K Track Circuit System Based on Risk Estimation[C]//JIA Limin,LIU Zhigang,QIN Yong, et al. Proceedings of the 2013 International Conference on Electrical and Information Technologies for Rail Transportation. Berlin Heidelberg: Springer-Verlag,2014: 383-392.

[13] CLAYTON R P, 闻映红. 电磁兼容导论[M].2版. 北京: 人民邮电出版社, 2007.

[14] ZHAO Linhai, WU Jianping, RAN Yikui. Fault Diagnosis for Track Circuit Using AOK-TFRs and AGA[J]. Control Engineering Practice, 2012,20:1 270-1 280.

[15] 中华人民共和国铁道部. 铁路信号维护规则技术标准Ⅱ[M]. 北京: 中国铁道出版社, 2008.