广义坐标变换在普通物理学中的一些应用

李文略（岭南师范学院基础教育学院，广东湛江 524037）



广义坐标变换在普通物理学中的一些应用

李文略
（岭南师范学院基础教育学院，广东湛江 524037）

摘 要文章举例阐述了广义坐标变换在力学和电磁学中的一些应用．应用广义极坐标变换和广义球坐标变换计算线椭圆环、椭圆盘和椭球刚体对任意轴的转动惯量；应用电多极展开的具体形式结合广义坐标变换，计算均匀带电线椭圆环、椭圆盘和椭球在远场处的电势．

关键词广义极坐标；广义球坐标；转动惯量；电多极势；椭圆环；椭圆盘；椭球

圆、椭圆、球、椭球是我们经常遇到的几何形体，在普通物理学中常常要处理与之相关的许多问题，而关于椭圆和椭球问题的处理往往是比较困难的．陈燊年［1］等应用广义球坐标变换巧妙地计算了电各向异性介质中带电椭球的电四极矩，受此启发，本文应用广义极坐标变换和广义球坐标变换计算与椭圆或椭球形状相关的物理模型的转动惯量和电多极势．

1 匀质线椭圆环、椭圆盘、椭球刚体的转动惯量

主轴坐标系O－xyz的坐标原点均建立在椭圆环、椭圆盘或椭球的几何中心处．设任意转轴通过原点，转轴在坐标系中的位置可以用方位角φ和极角θ来确定．在主轴坐标系中刚体的3个主转动惯量为Jxx，Jyy，Jzz，惯量积为零．应用转动惯量并矢式［2］可得刚体对任意转轴的转动惯量为

1．1 线椭圆环绕任意转轴的转动惯量

质量为m，线密度为λ，长、短半轴分别为a、b的匀质线椭圆放置在主轴坐标系O－xyz的O－ xy面上．在环面上取广义极坐标为第二类完全椭圆积分，椭圆参数由转动惯量的定义和垂直轴

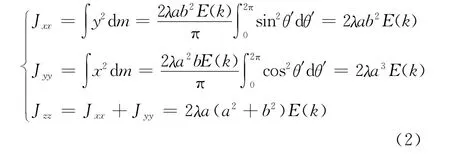
定理，计算出

将式（2）代入式（1）中，得线椭圆对任意转轴的转动惯量

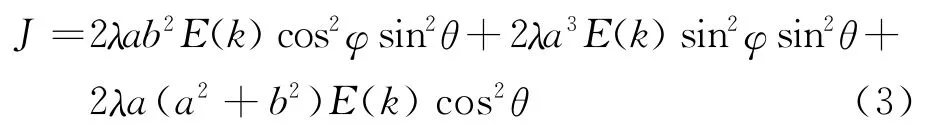
因线椭圆的周长L＝4aE（k），m＝4λaE（k），则式（3）也可改写为

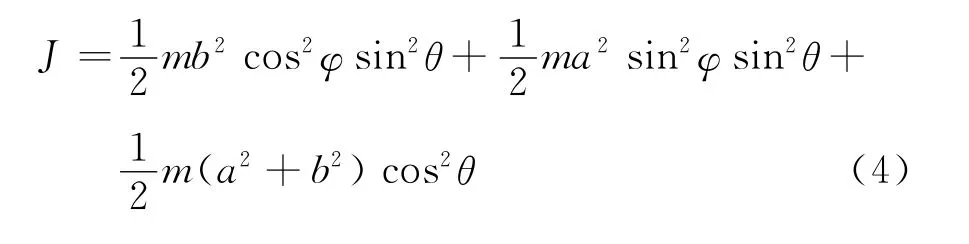
若令a＝b代入式（4），可得线圆环绕任意轴的转动惯量为代入式（3）中亦能得到该结果．

1．2 椭圆盘绕任意转轴的转动惯量

质量为m，面密度为σ，长、短半轴分别为a、b的匀质椭圆盘放置在主轴坐标系O－xyz的O－ xy面上．在盘面上取广义极坐标有和

由转动惯量的定义和垂直轴定理，计算

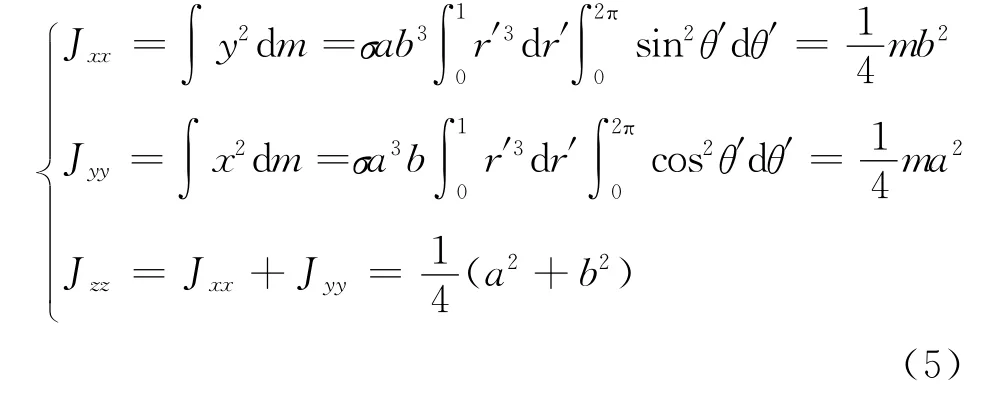
所得结果与文献［3］一致．将式（5）代入式（1）中，得椭圆盘对任意转轴的转动惯量

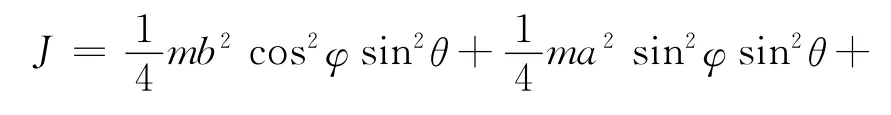
1．3 椭球刚体绕任意转轴的转动惯量

质量为m，密度为ρ，半轴分别为a、b、c（c≤b ≤a）的匀质椭球放置在主轴坐标系O－xyz中，椭球面方程为．取广义球坐标有．故同理计算出：由转动惯量的定义，计算

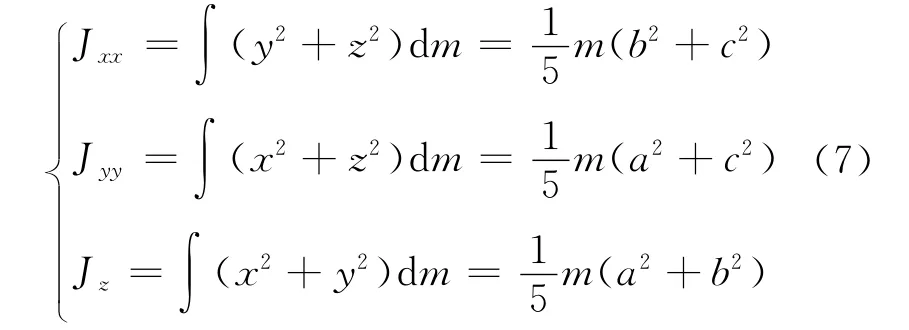
所得结果与文献［3、4］一致．将式（7）代入式（1）中，得椭球对任意转轴的转动惯量cos2θ．

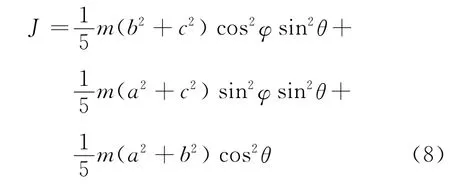
若令b＝c代入式（8），可得长旋转椭球绕任意轴的转动惯量为

若令a＝b代入式（8），可得扁旋转椭球绕任意轴的转动惯量为

若令a＝b＝c代入式（8），可得球体绕任意轴的转动惯量为，这是熟悉的结果．

2 均匀带电线椭圆环、椭圆盘、椭球的电多极势

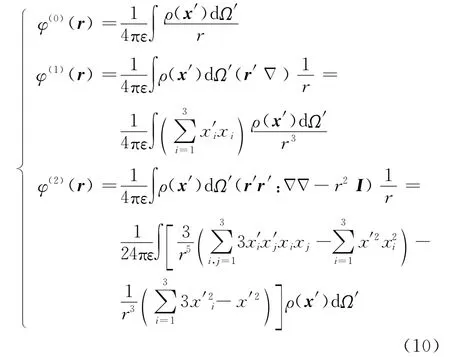
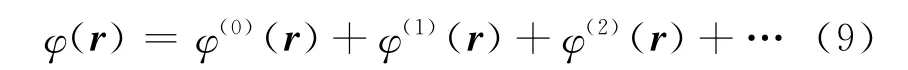
2．1 均匀带电线椭圆环的电多极势

带电量为Q，线密度为λ，长、短半轴分别为a、b的均匀带电线椭圆放置在坐标系O－x1x2x3的O－x1x2面上，应用电多极势的具体形式求其在远场点P（x1，x2，x3）处的电势．在环面上取广义极坐标与前文相同．因为x′3＝0，由电荷分布关于x1轴和x2轴对称，可知φ（1）（r）＝0．计算出将这些关系代入式（10）中计算电四极项，并连同φ（0）（r）代入式（9）中，可得线椭圆环在远场处的电势为

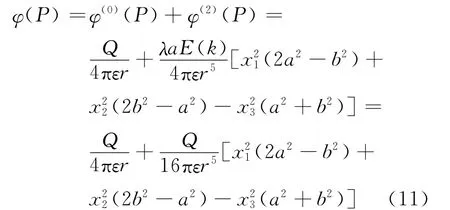
若令a＝b，代入上式可得半径为a的带电圆环在远场处的电势

2．2 均匀带电椭圆盘的电多极势

带电量为Q，面密度为σ，长、短半轴分别为

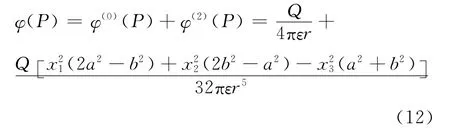
若令a＝b，代入上式可得半径为a的带电圆盘在远场处的电势

2．3 均匀带电椭球的电多极势

带电量为Q，密度为ρ，半轴分别为a、b、c （c≤b≤a）的均匀带电椭球放置在坐标系O－ x1x2x3中，椭球面方程为取广义球坐标与前文相同．由电荷分布关于x1轴、x2轴和x3轴对称，可知．计算出将这些关系代入

式（10）中计算电四极项，并连同φ（0）（r）代入式（9）中，可得椭球在远场处的电势为

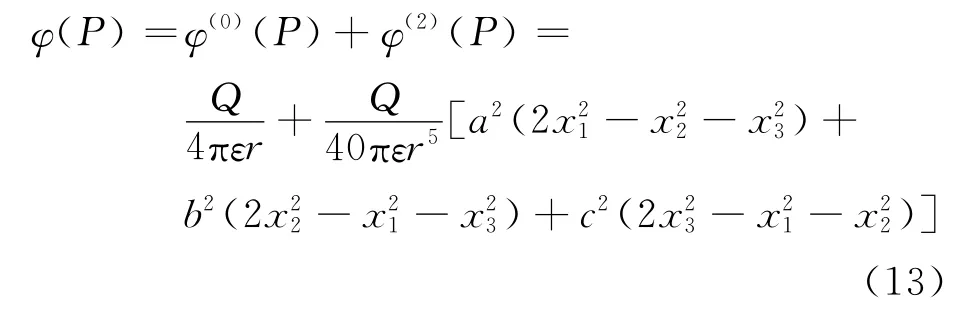
若令a＝b，代入式（13）可得扁旋转椭球远场电势

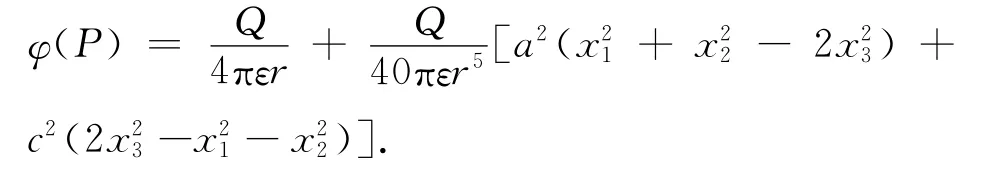
若令b＝c，代入式（13）可得长旋转椭球远场电势为

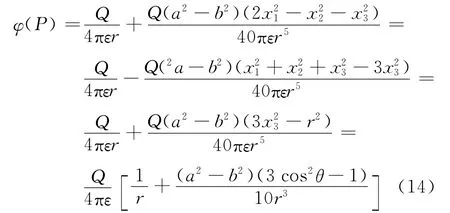
式中：x3＝rcosθ．所得结果与文献［5］应用球张量计算的结果一致．

若令a＝b＝c，代入式（13）可得半径为a的带电球在远场处的电势为这是所熟悉的结果．

3 结语

对于涉及以线椭圆环、椭圆盘和椭球为物理模型的一些普通物理学中的问题，应用广义坐标变换无疑是解决这些问题的较为简捷的数学方法，文中给出了求这些模型的转动惯量和电多极势的例子．将该方法引入课堂教学中，能有效地提升学生处理相关物理模型问题的数学能力．

参考文献

［1］ 陈燊年，洪清泉，王建成．介质为各向异性的电磁场［M］．北京：科学出版社，2012：74、112－127．

［2］ 李文略．惯量张量并矢式及其应用［J］．河南教育学院学报：自然科学版，2014，23（4）：47－51．

［3］ 孙艳平，等．复杂椭圆形薄板和椭球体转动惯量［J］．辽宁科技大学学报：2011，34（4）：352－354．

［4］ 刘红．椭球壳及椭球体转动惯量的简易推导［J］．物理与工程，2012，22（4）：61－62．

［5］ 袁德荣．球张量的多极展开法［J］．湖北大学学报：自然科学

版，1988（1）：94－98．

审稿意见和作者修改说明摘录：

原稿题目：计算一类均质薄板刚体转动惯量的新方法

原稿评审意见：首先文中（2）和（3）所给的结果不是什么新结果，而是在几乎任何理论物理教材中都会找得到的结果．当然作者采用自己的做法得到了它们还是值得称道的．但在文中称为“新”是不合适的，因为这只是对作者是新的，对那些了解后续分析力学课程结果的人却是标准的教科书结果．再，从式（6）出发利用转动对称性计算转动惯量，或电磁学中的电四极距，或极化介质的电场能等在大学物理课中早有论述，具体可见费曼著名的三册书中的第二册中的第31章，那里详细讲授了如何应用对称性简化计算这些量．即使这样，本文所讨论的具体例子2．1，2．2 和2．3还是与费曼的讨论有所不同．本文是基于主轴坐标系的结果，利用转动给出任意情形下的结果，虽然这略显简单和平庸；但这确如作者在文章最后所述“有助于加深学生对惯量张量的理解，并能拓宽学生计算刚体转动惯量的数理思路”．本文只是所给的例子略显单薄，应再多给几个，并改进对此做法的提法．

作者修改说明：要充实文章例子并非易事……机缘巧合下拜读了陈燊年教授等所著的《介质为各向异性的电磁场》，其中她巧妙地应用球坐标积分变换计算了各向异性介质中椭球的电多极矩，却避免了椭圆积分运算，刚好专家的评审意见中的“电磁学中的电四极距”也浮现在脑海中．于是，产生了修改的灵感，也许这些都是有联系的……

现有文献计算椭圆、椭圆盘和椭球的计算方法大多需要用到特殊函数，既然球坐标积分变换可计算电多极矩，自然也可迁移计算转动惯量，再结合原始稿件中求任意转轴的转动惯量的写作初衷就得到了修改稿中的第一部分了．另外，电磁学中计算电多极势，大多采用计算电多极矩再进行矢量或张量间的点乘运算，然而若能得到电多极展开的具体形式再结合广义坐标变换的方法，则计算就简便多了，于是就完成了文章的第二部分．

回想学生时期的我，遇到椭圆积分就感到头疼，这也许也是我的学生现在烦恼的事吧．广义积分的变化方法如果能应用于教学中，还是能成为学生的头疼“缓解药”的，当然椭圆积分还是要扎扎实实地学好．于是文章的题目就成了《广义坐标变换在普通物理学中的一些应用》．文章的改动非常大，可以说是另一篇新的文章了；但是从修改的过程和写作灵感的获得来看，却得益于专家的评审意见，可看作原始稿的延续吧．

SOME APPLICATIONS OF GENERALIZED COORDINATE TRANSFORMATION IN GENERAL PHYSICS

Li Wenlue
（College of Basic Education，Institute of Lingnan Normal University，Zhanjiang，Guangdong 524037）

AbstractSome applications of generalized coordinate transformation in mechanics and electro magnetism are described by examples．Generalized polar coordinate and spherical coordinate transformation are applied to calculate the moment of inertia of a linear elliptic ring，elliptic disc and ellipsoid rigid body to an arbitrary axis．The electric potential in the far field of uniform charged wire，elliptic disc，and ellipsoid body are calculated by applying the specific form of electric multipole expansion combined with the generalized coordinate transformation．

Key wordsgeneralized polar coordinates；generalized spherical coordinates；moment of inertia；electric multipole potential；ellipse ring；elliptical disc；ellipsoid

作者简介：李文略，男，讲师，主要从事基础物理课程的教学与研究．physics2009ed＠126．com

收稿日期：2014－08－08