存在局部损伤时转动弹性支承铁路梁桥的位移影响线分析

张延庆，孙 珂

(北京工业大学 建筑工程学院，北京 100124)

铁路桥梁多采用梁式结构。在梁式桥的传统分析方法中，结构边界通常被简化为理想铰接或刚接。在实际工程中，梁式结构边界一般不是理想支承，如理论上铁路简支梁桥的端部转角沿桥跨方向的变化率无穷大，实际由于钢轨等具有一定的抗弯刚度，端部转角受限；刚接的梁式结构存在一定柔性[1]；连续梁中的相邻跨可互为弹性支承[2]。非理想支承在影响结构内力分布的同时，也会影响其变形分布。

在役桥梁结构作为铁路及公路运输的重要基础措施，桥梁检测成为其发展过程中不可少的一部分。及时的损伤检测可以保证桥梁在使用期限内有足够的安全储备。现阶段有多种桥梁检测分析方法，如采用基于固有频率的损伤评估法[3]、利用静力测试数据的模型修正方法[4]和基于模态振型的损伤识别方法[5]等，这些方法由于种种原因在工程应用中存在一定局限。为了更全面分析桥梁的工作状态，有学者提出利用影响线加载进行检测的方法[6]。影响线加载对于结构的指定截面具有全局施加荷载的优点，能反映该截面在移动荷载作用下的响应变化，避免了传统检测方法识别工况少、对局部损伤不敏感的缺点。随着GPS和激光等工程测量技术的日益发展，利用较易得的位移数据分析结构工作状态已成为可能[7，8]。

目前利用影响线对梁式结构进行损伤识别的方法主要集中在简支梁这一静定结构，文献[9，10]利用位移影响线的二阶导数实现对理想支承下一维简支梁的损伤识别。文献[11]提出一种基于简支梁位移影响线对称位置差值指标进行损伤定位的方法。针对两端有一定转动刚度的单跨梁或连续梁桥中的一跨等类似超静定结构的位移影响线分析较少涉及，缺少理论支持。

为分析这种非理想支承形式下梁式结构的工作状态，本文建立端部存在转动弹性支承的铁路梁桥模型。首先利用支承处的变形协调条件建立该模型的力法方程，得到存在局部损伤的梁式结构在移动荷载下的内力公式；根据虚功原理得到该结构任意测点的位移影响线显式表达式。利用这类较易得到的全局性数据，分析局部损伤与弹性支承间的关系，得到弹性支承刚度Kb与局部损伤共同作用下位移影响线及其曲率的变化规律。本文为拓展影响线在桥梁领域应用及适用性提供一定的理论支持。

1 转动弹性支承梁式结构内力分析

如图1所示，建立存在局部损伤的转动弹性支承梁式结构模型，该结构跨长为l，集中荷载FP作用于x点处。该类结构具有以下特点：属二次超静定结构；两端支座处有转动弹性支承，Kb1、Kb2表示两转动支承刚度；区间(a，b)处出现局部损伤；集中荷载位置沿桥跨方向变化。

图1 存在局部损伤的转动弹性支承梁式结构模型

1.1 力法方程

该模型作为超静定结构体系，无法直接通过平衡方程求解。为此，通过拆除两个多余转动支承将原模型等效为一个简支梁的基本体系，如图2所示。图2中X1、X2代表转动支承处的弯矩。

图2 基本体系

( 1 )

根据叠加原理，图1所示状态可由荷载FP、X1及X2分别作用在基本结构上的相关位移相加得到。其中δij(i，j=1，2)表示Xi(i=1，2)=1分别单独作用在基本结构上沿Xi(i=1，2)方向的位移；Δ1P，Δ2P表示FP作用时基本结构沿Xi(i=1，2)方向的位移。利用结构的变形协调条件得到该模型的力法方程为

( 2 )

1.2 系数求解

影响线是在移动荷载沿结构移动时得到的某指定量值变化规律的图形。本节推导移动荷载FP作用下梁式结构力法方程中各系数的表达式。

计算前做如下假定：非损伤区域结构截面尺寸及材质相同；不考虑剪切变形的影响；弯曲刚度为EI，在区间(a，b)处弯曲刚度定义为kEI来模拟局部损伤，其中k为刚度折减系数[9]。

为了区分移动荷载的位置x，引入一个过渡坐标系x′，如图3所示。得到基本结构分别在移动荷载FP、单位力X1=1及X2=1作用下在任意截面位置x′处的内力公式

(3a)

(3b)

(3c)

图3 MP图

Φ1(x，(a，b))

(4a)

(4b)

式中：Φ1(x，(a，b))、Φ2(x，(a，b))表示局部损伤对FP作用下基本结构相应位移的影响函数。此时由于移动荷载与损伤区间(a，b)的位置关系不确定，该函数需分段表示。

当x≤a时

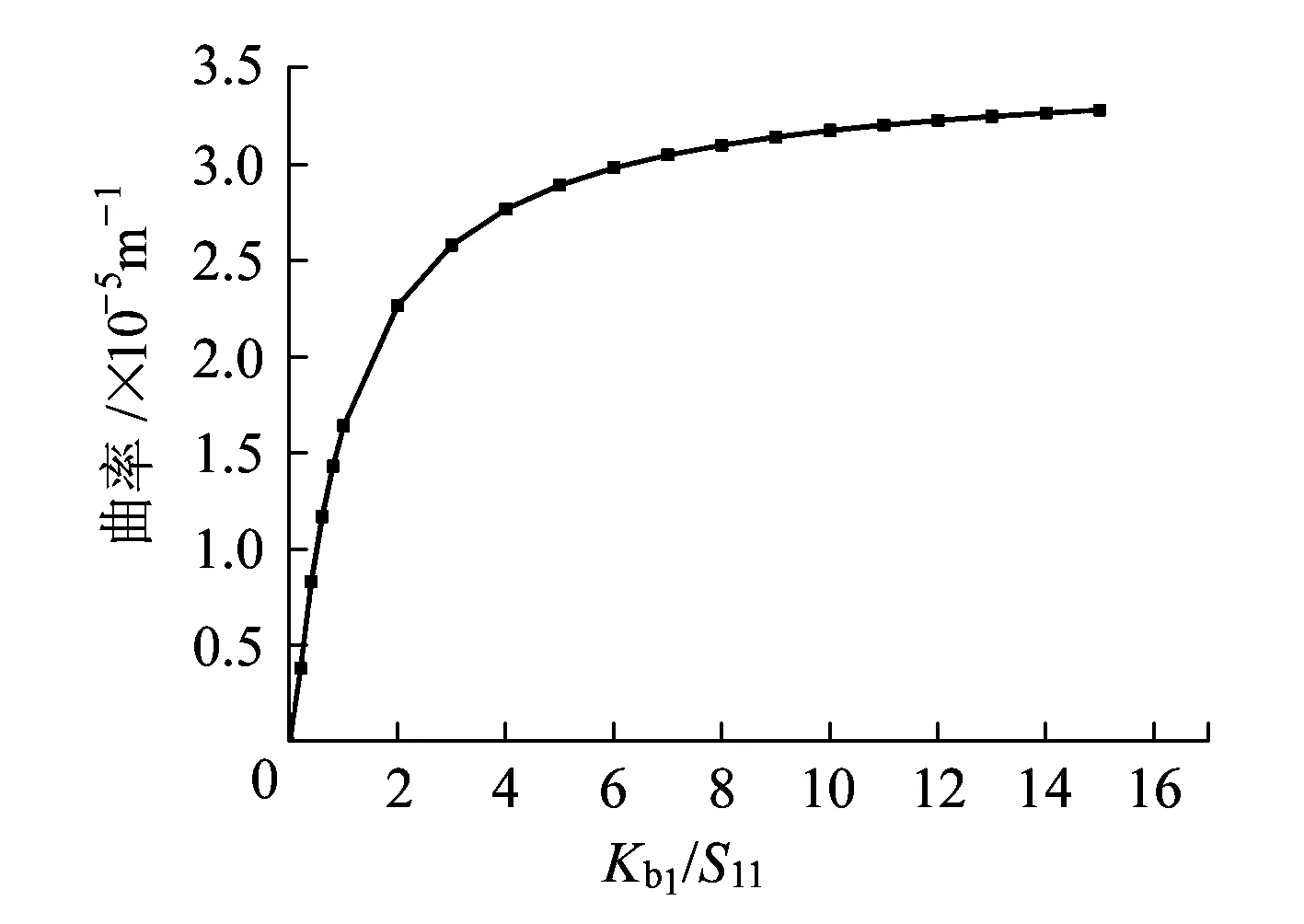
当a

当x≥b时

从分段公式可以看到，除了移动荷载位于损伤区域(a，b)之间时，局部损伤引起的基本结构位移变化都是关于荷载位置x的一次函数。

(2)单位力单独作用时基本结构相应位移系数

(5a)

(5b)

(5c)

从式( 5 )可以看出，系数δij与移动荷载的位置无关，只与局部损伤位置及损伤程度有关。

1.3 弹性支承处反力及内力影响线

将上面系数代入式( 2 )可以得到两个未知力的表达式，即两个转动支承处的弯矩MB1，MB2。

( 6 )

由式( 4 )～式( 6 )可知，支承处内力MBi为荷载位置x的三次函数，分母项为损伤后结构的相关刚度常数。

根据叠加原理，测点S处弯矩M影响线公式表示为

( 7 )

2 位移影响线解析公式

对于具有转动弹性支承的结构，利用虚功原理求导任意测点S处的位移影响线，见式( 8 )。由于基本结构两端无约束转动刚度，与弹性支承相关的位移ΔKC为零。

( 8 )

引入过渡坐标系x′(图4)，s表示位移观测点S的位置，x表示荷载作用位置。

图4 位移Δ求解简图

当单位荷载作用在测点S时，基本结构上截面x′的弯矩表达式Ms可以将FP=1及x=s代入式( 3 )得到，在此不列出。在移动荷载FP作用下截面x′的弯矩MP为

( 9 )

如图4所示，由移动荷载FP与局部损伤区间(a，b)及测点S的位置关系可以将结构分为四段分析：①0

Δsx=Δ1(基本结构)+Δ2(与弹性支承相关)

=Δ1，无损+Δ1，(a，b)+Δ2，Kbi+Δ2，(Kbi，(a，b))

(10)

式中：Δ1(基本结构)表示存在局部损伤时基本结构测点S的位移影响线，可以由未损伤前基本结构位移Δ1，无损和与局部损伤有关位移Δ1，(a，b)的叠加来表示。

Δ2(与弹性支承相关)表示该梁式结构中与弹性支承相关的位移，Δ2，Kbi表示与转动弹性支承内力有关的位移变化量；Δ2，(Kbi，(a，b))表示与弹性支承刚度及(a，b)有关的量。此时要注意：由公式( 6 )求解转动支承内力也与损伤(a，b)有关，本文为了表述清楚，人为将Δ2，Kbi，Δ2，(Kbi，(a，b))分开表示。

3 转动刚度Kb对位移影响线的影响

从式(10)可以看到转动弹性支承和局部损伤相互作用与该类梁式结构位移影响线的关系。为了进一步观察转动支承刚度对影响线的影响及出现局部损伤时位移影响线的敏感性，结合数值分析编制相应计算程序，对某跨度为40 m梁式结构进行竖向位移影响线分析。该结构弹性模量E=3.3×107kN/m2，惯性矩I=2.387 5 m4，荷载FP=400 kN。

如图5所示，以两跨连续梁中左跨为分析对象，将原结构简化为如图5(b)所示端部转动弹性支承的单跨结构，分析Kb变化时该类结构的位移影响线特点。通过简化可以只分析左跨，将结构分析工作量降低，在工程中也可以减少数据处理量。

图5 简化过程

针对图5(b)结构，分析转动支承刚度Kb1变化时，跨中测点位移影响线的变化规律，如图6(a)所示。由图6(a)可以看到弹性支承刚度Kb1减小时，位移影响线整体数值变大，以测点为界靠近转动支承一侧的位移数值变化较大。图6(b)给出3个常用测点(跨中及两个四分点)在转动支承刚度变化前后影响线的差值。从图6(b)可以看到，跨中测点的位移影响线变化最大；两个四分点中靠近弹性支承测点(s=3l/4)数值的变化明显大于远离端测点(s=l/4)的变化。

(a)跨中位移影响线

(b)转动刚度变化前后位移影响线差值图6 Kb1变化时位移影响线

由式(10)可知，当转动弹性支承刚度变化时，位移影响线的峰值位置也在变化，在远离弹性支承处(s=l/4)变化较明显。图7为弹性支承刚度Kb1变化时四分之一跨位移影响线峰值位置的变化。从图7可以看到，随着转动支承刚度Kb1增大，四分之一跨处的位移影响线峰值位置从0.45l向0.4l移动。而跨中及四分之三跨处的位移影响线峰值位置随转动支承刚度Kb1变化，分别出现在跨中及0.55l附近，变化幅度较小。

图7 Kb变化时s=l/4处位移影响线峰值位置变化情况

通过上述分析，可以总结出一般规律：两端都存在弹性支承时，以测点为界，靠近转动支承刚度较大的一侧在刚度变化时影响线数值变化大；针对常用测点(跨中测点及两个四分点)，当转动刚度变化时，跨中测点的位移影响线变化最大，靠近转动刚度较大支承四分点的变化大于另一个四分点的变化；随着转动弹性支承变化，位移影响线的峰值位置也出现变化，远离转动弹性支承一侧的测点峰值位置变化较大。

4 转动弹性支承及局部损伤共同作用对位移影响线的影响

图8分别给出该结构在区间(0.3l，0.4l)处出现损伤时跨中影响线Δsx、Δ1及Δ2的曲线，其中Δ1也可以表示简支梁结构出现局部损伤时的位移影响线。由图8可以看到对于简支梁，转动支承的存在使该结构影响线的整体数值减少，但在缺少原始数据的情况下不能直接判断局部损伤对位移影响线的影响程度，需要借助进一步的数值处理来观察。

图8 位移影响线组成图

当该类梁式结构出现局部损伤时，从式(10)可以看到弹性支承对局部损伤引起的影响线变化是有影响的。如图8所示，直接利用位移影响线并不能判断局部损伤的存在。有的研究表明位移曲线的曲率在简支梁的局部损伤识别中有较好效果[10]。以简支梁(Kb=0)、等跨连续梁其中一跨及固端梁(Kb=∞)为例，通过对位移影响线进行曲率求解，进一步分析对比转动支承刚度及局部损伤共同作用时影响线的变化情况。

设曲率为κ(x)、Δ为竖向位移，根据几何关系曲率方程可以表示为：κ(x)≈Δ″(x)。在工程中通过仪器测得某测点的位移影响线后，利用二次差分公式即可求出曲率。

(11)

式中：d为移动荷载两个临近点的距离。

利用位移影响线数据及式(11)分别得到简支梁、连续梁选定跨及固端梁跨中位移影响线曲率，如图9所示。

图9 位移影响线曲率曲线

从图9可以看到，这3种结构的曲率在损伤位置出现突变，与弹性支承相关的位移Δ2在损伤位置也有突变，但变化趋势与整体变化趋势相反，即对局部损伤引起的变化有减弱作用。

表1 不同支承条件下相关荷载位置*曲率数值

*：相关荷载位置是指结合图9在表1中给出的荷载在非损伤影响区域及突变区域峰值的坐标。

表1给出了这3种支承条件下，相关荷载位置处的曲率数值及比较，其中：Kbi/Sii表示转动支承与结构的相关刚度比(在前面公式中表示为Kbiδii，Sii为i端部的转动刚度)，突变区域峰值预测值根据表中荷载在非损伤影响位置时的曲率数值线性插值得到。从表1可以看到突变峰值实际值与预测值随着弹性刚度的增大而减少，但其相对变化比例不会随着转动支承刚度的增大而变化。

通过图8和图9进一步发现，曲率曲线除了在局部损伤处有突变，当Kb>0时该类结构在转动弹性支承处的曲率数值也不为零。为了观察转动支承处的曲率数值变化，给出此时位移影响线曲率相关系数表达式。

(12a)

(12b)

从式(11)可以看出，弹性支承处的曲率大小由测点位置、结构刚度、转动支承刚度及局部损伤共同决定。当测点位置确定时，转动弹性支承处的曲率数值可以体现出结构刚度与转动支承刚度对位移影响线的影响程度。

为了进一步观察不同转动刚度对该结构损伤分析的影响，图10给出不同弹性支承刚度Kbi边界处曲率数值的变化规律，其中横坐标选取Kbi/Sii。

图10 边界处曲率数值变化曲线

从图10可以看到，随着转动支承刚度逐渐变大，转动弹性支承对位移影响线的影响并不呈线性增加，当增加到一定程度后影响变化逐渐不明显。结合工程实际，当转动刚度相对较小时，端部转动刚度变化引起的曲率变化明显；转动刚度较大时，端部转动刚度变化引起的曲率变化不明显，要注意增加在梁端部处损伤检测。

5 结论

本文利用支承处的变形协调条件，推导得到转动弹性支承条件下梁式结构的力法方程，利用虚功原理求解存在局部损伤时该类梁式结构内力及位移影响线显式表达式。通过理论与数值分析得到以下结论：

(1)本文给出的显式表达式可直观表示转动弹性支承梁式结构的力学特性与局部损伤、转动支承刚度及结构相关转动刚度等因素的相互关系，揭示了这些因素共同作用下的位移影响线特点。将位移影响线表示为移动荷载下简支梁结构与弹性支承相关位移叠加结果，通过公式可直观显示弹性支承及局部损伤对位移影响线的贡献。

(2)通过数值分析，给出不同转动支承刚度时常用测点(跨中，两个四分点)位移影响线的变化特点：跨中测点位移整体数值最大；靠近转动刚度较大支承的四分点位移数值变化较大，远离刚度较大支承的四分点影响线峰值位置变化范围较大。

(3)利用位移影响线曲率对该类结构进行局部损伤分析：局部损伤处的曲率有突变，同时随着弹性支承刚度变大时，局部损伤引起的变化量减少，但相对变化比例不会发生改变。通过端部曲率数值变化曲线发现，随着转动支承刚度逐渐变大，转动弹性支承对位移影响线的影响呈非线性增加，增加到一定程度后该影响逐渐不明显。

(4)在工程条件允许下，利用该模型简化方法，可以只对连续梁等结构的选定跨进行检测分析，减少工程量和提高精度。

本文得到的公式可为该类铁路梁桥力学分析提供理论依据，并结合工程中易得的位移数据，为该类结构的结构检测与分析提供合理建议。

参考文献：

[1]SEKULOVIC M,SALATIC R.Nonlinear Analysis of Frames with Flexible Connections[J].Computers & Structures,2001,79(11):1 097-1 107.

[2]龙驭球,包世华.结构力学Ⅱ[M].2版.北京：高等教育出版社，2006:76-78.

[3]谢峻，韩大建.一种改进的基于频率测量的结构损伤识别方法[J].工程力学,2004,21(1)：21-25.

XIE Jun,Han Dajian.An Improved Method for Structure Damage Detection Based on Frequency Measurement[J].Engineering Mechanics,2004,21(1)：21-25.

[4]向天宇,赵人达,刘海波.基于静力测试数据的预应力混凝土连续梁结构损伤识别[J].土木工程学报,2003,36(11):79-82.

XIANG Tianyu,ZHAO Renda,LIU Haibo.Damage Detection of Prestressed Concrete Continuous Beam from Static Response[J].China Civil Engineering Journal,2003,36(11):79-82.

[5]陈淮，禹丹江.基于曲率模态振型进行梁式桥损伤识别研究[J].公路交通科技,2004,21(10):55-57.

CHEN Huai,YU Danjiang.Study on the Damage Detection in the Beam Bridge Using Changes in Curvature Mode Shape[J].Journal of Highway and Transportation Research and Developrnent,2004,21(10)：55-57.

[6]HUANG J,HARRY W SⅢ.Experimentally Determined Continuous Displacement Influence Lines for Bridges[C]//Structures Congress 2008(ASCE).

[7]FUCHS P,WASHER G,CHASE S,et al.Laser-based Instrumentation for Bridge Load Testing[J].Journal of Performance of Constructed Facilities,2004,18(4):213-219.

[8]ROBERTS G W,MENG X,DODSON A.Integrating a Global Positioning System and Accelerometers to Monitor the Deflection of Bridges[J].Journal of Surveying Engineering,2004,130(2):65-72.

[9]杜永峰，刘云帅，王晓琴.基于挠度差值影响线曲率的简支梁桥损伤识别[J].桥梁建设,2009(4):80-83.

DU Yongfeng,LIU Yunshuai,WANG Xiaoqin.Damage Identification of Simply-supported Beam Bridges Based on Influence Line Curvature of Deflection Differential Values[J].Bridge Construction,2009(4):80-83.

[11]SUN K,ZHANG Y Q.Analysis of Displacement Influence Line Characteristics of Simply Supported Beam with Local Damage[J].Advanced Materials Research,2014,919-921:364-368.