让数学课堂成为艺术的殿堂

黄明翠

[摘 要]数学是一门逻辑性强的学科。教师要想将抽象、严密的逻辑推理过程直观形象地展现出来，必须充分挖掘教材资源，寓情趣于知识之中，使学生产生强烈的求知欲望，在充满激情的探索中，促进学生创造力的提升，让数学教学更具生命力。

[关键词]形象 体验 情趣 创造 思维 想象 发展 效率

[中图分类号] G623.5 [文献标识码] A [文章编号] 1007-9068（2016）11-023

数学是一门逻辑性强的学科，思维含量高，不像语文课那样充满诗情画意、跌宕起伏，所以数学课稍不注意就会变得枯燥乏味。因此，数学课堂中，要想将抽象、严密的逻辑推理过程直观形象地展现出来，教师必须充分挖掘教材资源，寓情趣于知识中，借助学具、教具、多媒体等手段，辅以亲切、感人的艺术性语言，唤起学生的学习热情，轻松愉快地把学生带进瑰丽的知识殿堂。

一、重形象，促思维

万物皆有形，形象性是艺术的外显特征，数学课堂同样需要形象性。教师只有善于引导学生在具体可感的形象中完成从生动直观向抽象概括的转变，才能使数学课堂生动、鲜活。因此，课堂教学中，教师可通过数形结合、类比等方法，引导学生在充分感知、深入探索中理解数学概念，发现数学规律。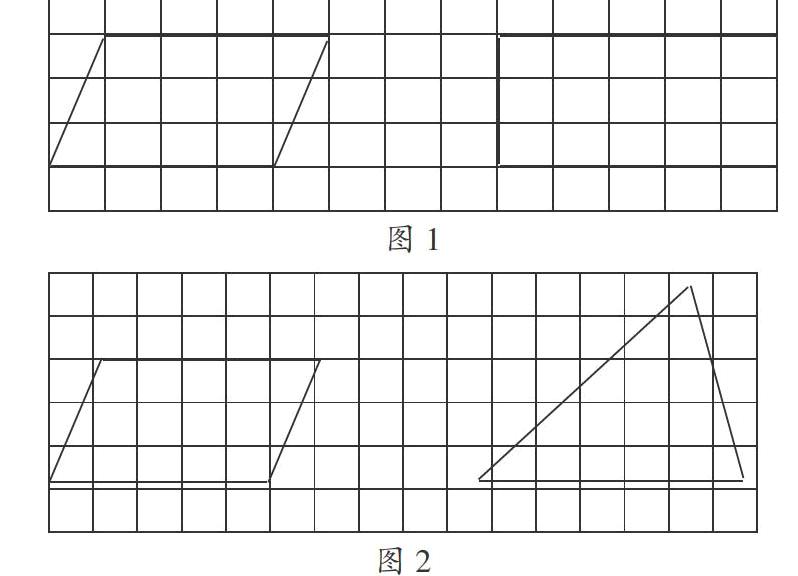

例如，在“认识梯形”一课教学中，教师出示课件，通过举例来引导学生探究。

师（课件出示一个足球门）：我们学校西操场就摆放着两个足球门，它们的正面方向是一个梯形，再看这是什么？

生：汽车，它的挡风玻璃被设计成梯形。

……

师：同学们，这是堤坝，它的横截面也是一个梯形。刚才你们提到了梯子，谁能指出这个梯子里面的梯形在哪儿？有吗？

……

在学生自学梯形的各部分名称后，师说道：“通过自学，结合黑板上的这两个梯形，你介绍一下梯形的各部分名称。”“老师给你提供梯形各部分的名称，你能正确的标注出来吗？”……这样教学，就把书上静态呈现的知识变成可以在手上拿放、拼摆的活生生的知识，不仅形象具体，而且加强了学生的记忆，使学生的理解更加深刻。当学生自学梯形的各部分名称之后，教师拿出一个梯形并提问：“你能说出它的各部分名称吗？”在学生对着梯形依次说出各部分名称后，教师又顺手把手上的梯形转了转，问：“现在你还能说出它的各部分名称吗？我来指，你来说。”这样可让学生的思考不断深入，将简单、浅显的认识变成活生生的知识，使课堂瞬间灵动起来。同时，这样教学还避免了学习水平中下的学生死记硬背概念的现象。最后，教师总结：“看来，不管梯形的位置发生什么变化，互相平行的两条边都称为梯形的上底和下底。”通过直观形象的演示，让学生对知识的本质有了深刻的理解，进一步促进了学生思维能力的提高。

二、重体验，促发展

《数学课程标准》中指出：“要让学生在现实情境中体验和理解数学，体验数学知识之间的内在联系，初步形成对数学整体性的认识，通过获得成功的体验和克服困难的经历，增进应用数学的自信心。”课堂教学中，教师可以根据教学内容和学生的年龄特点，运用激励猜想、动手操作、实践验证等方法，优化教学过程，获得好的教学效果。

例如，在学生认识梯形各部分的名称后，教师问：“通过自学，你还认识了什么？”在学生回答哪一个是直角梯形、哪一个是等腰梯形并说明为什么后，教师又问：“有什么方法可以验证等腰梯形的这两条腰是相等的？”学生通过动手操作，发现等腰梯形的两条腰完全重合，这说明等腰梯形的两条腰相等、两个底角相等。然后教师揭示：“等腰梯形还是我们学过的轴对称图形，对折后可以变成两个直角梯形。”这样教学，引导学生亲历了从等腰梯形的一半创造出直角梯形的过程，使学生在体验中发现数学知识，在数学活动中总结数学规律，增强了学习数学的信心。在学生获得成功的快乐的同时，培养了他们观察、比较、合作等能力，促进了学生个性的发展。

三、重情趣，促效率

“情感是一切艺术之母。”数学教学作为一门科学，主要运用理性，以理服人；数学作为一门艺术，则主要运用情感，以情感人。首先，教师在数学教学中要用自己饱满的教学热情，激发学生积极学习的情感；用趣味性、激励性、富有悬念、饱含幽默的语言，唤起学生的学习兴趣；用清晰、和谐、有韵律及节奏感的语调，使学生的学习热情不断受到激励。

例如，在本节课的巩固练习当中，教师可这样激励学生：“祝贺你们完成第1题，接下来看第2题，题目叫‘美丽的相遇。”这样一句“美丽的相遇”似乎一下子把学生带入充满浪漫和富有诗情画意的美丽情境之中，使学生的注意力深深地被吸引了。于是，教师顺势引导：“同学们，你们看，有这样一个平行四边形和长方形（如图1），如果它们继续移动，就会相遇并交叉重叠，你们觉得重叠部分会是什么图形？”随着精美的课件动画演示，教师没有马上揭示答案，而是制造一个趣味的小悬念：“我先卖个关子，还有两个像这样的图形，即平行四边形和三角形（如图2），它们继续移动也会交叉重叠，你们认为重叠部分会是什么图形？”生答：“梯形。”“确定是梯形？你们看（课件演示），它们相遇了，重叠部分是——”生：“梯形。”“好，现在问题来了，为什么这两个图形的重叠部分是梯形？”学生的回答也相当精彩：“因为平行四边形有两组对边分别平行，三角形与它重合，只用到了一组对边。”师继续提问：“现在我们再来看看，原来这两个图形相遇后会是什么图形？为什么？”生：“相遇后会是平行四边形，因为平行四边形和长方形都是两组对边分别平行，重叠后还是两组对边平行。”……通过教师的层层设疑和充满情趣性的言语引导，再辅以精美的课件演示，不仅激发了学生的求知欲望，而且让他们牢固掌握了梯形的本质特征。

在下一练习环节中，教师又设计了一道充满趣味的题目“调皮的C点”（如下图）：“这两条平行线上有4个点，形成一个四边形ABCD，在这4个点中，数C点最调皮，它喜欢在这条线上跳来跳去。当它往右边移动，这时候ABCD变成什么图形？同学们，如果C点再调皮一次，把B点的位置给占领了，这个图形就变成了什么？”

在学生回答后，教师趁机小结：“是啊，又产生了新的图形——三角形。不管C点是向左还是向右，当图形的某些条件发生变化时，这些图形就会相互变化。”……学生在这样充满情趣的练习中，既深刻掌握了梯形的相关知识，理解了图形之间的相互联系与变化，使知识融会贯通，又兴趣盎然地投入课堂学习之中，极大地提高了课堂教学的效率。

可见，在数学教学的实践与探索中，情趣教学已显示出其独特的魅力。因此，教师在教学中不仅应将师生关系看做是“教”与“学”的关系，更应该与学生有一种情感上的渗透和升华，进而提高学生学习数学的积极性。教师只有坚持以学生为主体，重视情感教育，培养学生的学习兴趣，才能更有效地提高数学课的教学质量，使课程改革真正落到实处。

四、重想象，促创造

想象力是创造力的基础，是在感知材料的基础上，重新创造出新事物的能力。有教育家说过：“想象力是人才的翅膀，有作为的人只有借助想象这对翅膀，才有可能发挥创造的才能。只有想象力丰富了，孩子的创造潜能才会被挖掘出来。”爱因斯坦也曾说过：“想象力比知识更重要，因为知识是有限的，而想象力概括着世界上的一切，推动着进步，并且是知识的源泉。”同时，创造是通过想象逐步积累而成的，只有丰富的想象，学生才会有创造，形成创造性的思维能力。

如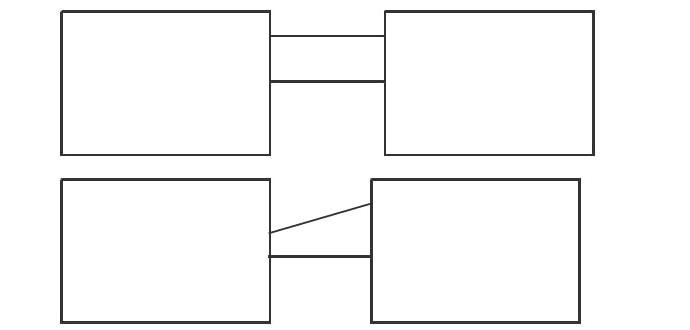 在最后的拓展练习中，教师又设计了这样一道题（如下图）：“有一个四边形，它的两边被两块布遮住，露出了中间部分，这有可能是什么图形？如果被遮住的两条边是不平行的，有可能是什么梯形吗？”问题提出后，学生发挥想象进行各种猜测，并随着课件中两块活动布的展开时而开怀大笑，时而恍然大悟。这里，学生的思维受到强烈撞击，师生情感相互交融，轻松和谐的氛围再次将课堂教学推向高潮。课尾，教师顺势激励学生：“大家能够根据遮住的部分想象出这么多的图形，真棒！现在我们再把两块布拉起来，这时平行的对边变成不平行了，你觉得原来这是一个什么图形？”

当学生想象并比划出可能是梯形、三角形、平行四边形，甚至可能是五边形或其他图形时，学生的视野得到了进一步开阔。这样通过不断的观察、想象，再根据条件进行推理、判断，既使学生深刻掌握梯形的特征以及图形之间的相互转化关系，又提升了学生的创造性思维能力。

哲学家康德说过：“想象力是一股强大的创造力量，它能够从实际自然所提供的材料中创造出第二自然。艺术的生命在于创造，创造性更是数学教学的生命力。”因此，教师在教学中要善于培养学生的想象力，使学生产生强烈的求知欲望，提升他们的创造力。在数学教学与艺术教育的有效整合中，学生的学习热情高涨，数学课堂变得鲜活生动、富有情趣，学生在浓厚的艺术氛围中快乐着、成长着、收获着，真正将数学课堂变成为学生的艺术殿堂。

（责编 杜 华）