用研究性学习方式开设《抛物线的标准方程》公开课的反思
2016-05-06王军成
王军成
摘 要: 对于开设《抛物线的标准方程》这一节公开课,作者选择了“研究性学习”教学法。此法是十分具有创造性与挑战性的教学新模式。在课前要做好充分准备,在教学过程中让学生在合作中探索知识,获得知识与方法,理解概念与原理,也需要时刻参与引导学生更好、更深入地进行探究,突出体现学生的主体地位与老师的主导地位。
关键词: 研究性学习模式 教学设计 引导与可控 教学反思
一、环节设计要全面。
本次环节设计分为:教学目标的定位,课前准备,课堂展示,课堂研究,课堂交流,课堂汇报,课堂训练与课后拓展等环节。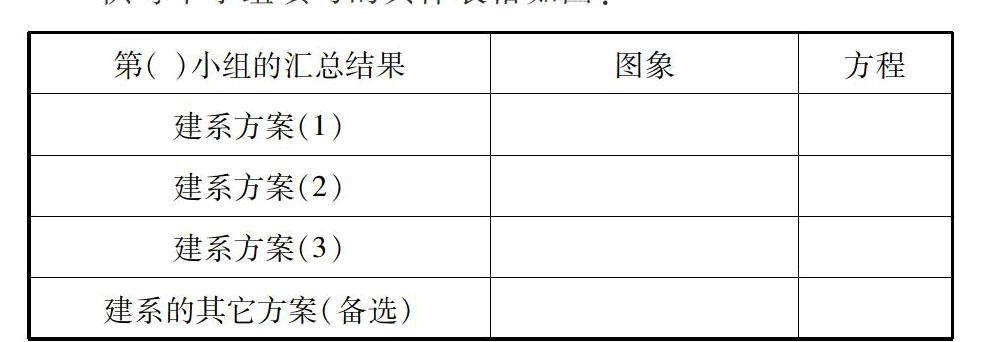
本课的教学定位是:重点是抛物线的定义和标准方程;难点是利用抛物线定义画抛物线的图像及标准方程的研究。
活动设计:课前给出问题、课上学生合作交流、老师引导研究方程得到最佳结果、巩固、拓展。
课前准备:将重难点分散到课前,提前研究,而且本节课首先是具体的操作问题,有一定难度,课前准备是很重要的。
课前具体的材料问题就是:若平面内一个动点Q到一定直线L与一个定点F的距离相等,尝试画出动点Q的轨迹。
供每个小组填写的具体表格如图:
二、准备工作要细致全面,课前设想要充分。
研究性学习法实施之前要做好细致的准备工作,不能太粗线条,每一个环节都要精心设计。
引入课题的设计:开门见山,课前研究结论在小组内交流,然后小组代表展示。如果大多数学生都能画出下面的这个图形,则说明学生已理解抛物线定义并会初步应用了。
(一)对于难点:用定义画“抛物线图像”的课前作业,我也准备了充分的素材,自己利用定义的方法画出了三条“抛物线”,加强对定义的理解与应用。在课堂上利用多媒体展示,启发学生思维。
(二)适时给出抛物线的定义:前面的交流学习过程一结束就由学生全面描述抛物线的轨迹的形成过程并给出定义:平面内与一定点F和一条定直线l的距离相等的点的轨迹叫做抛物线(定点F不在定直线l上)。定点F叫做抛物线的焦点,定直线l叫做抛物线的准线。(这里追问为什么定点F不能在定直线l上?学生研究特殊情况发现是一条直线。)
三、课堂上要实时的追加问题继续研究,同时要给学生一个“有限的空间”展开研究。
设定点F到定直线l的距离为p(p为已知数且大于0)。下面,我们来求抛物线的方程。怎样选择直角坐标系,才能使所得的方程取较简单的形式呢?
首先在黑板上画出四幅图,目的就是给出一定的限制,使他们出现四种情况。
让学生分小组充分议论,老师辅导他们完成方程推导过程。最后每一组展示建立直角坐标系的几种方案。(如果表达不够全面,补救方案是其他小组补充我启发,最后引导出结果。)
接着老师要引导学生比较所得的4个方程,应该选择哪些方程作为抛物线的标准方程呢?学生都会感受到建系的区别,同时又会感受到实质都相同,这样进一步加强了学生对数学美的认识,从而喜欢上数学的简洁严谨之美。
由于焦点和准线在坐标系下的不同分布情况,抛物线的标准方程有四种情形(见课本)。
四、研究性学习的课堂“不应止步于课堂”而需要提供拓展研究的材料(供学生课后自主探究)。
例如本课我提供了如下拓展材料:
(1)求证:(2)在工程中,画拱宽为2a,拱高为h的抛物线,常用下面的画法:
1)作矩形ABCD,使得AB=2a,DA=h;
2)分别取CD,AB的中点O,H把线段DA,OD,HA各n等分;
3)如图连线得到各交点,将交点连成光滑曲线,就得到抛物线的一半;
4)同样方法画出另一半。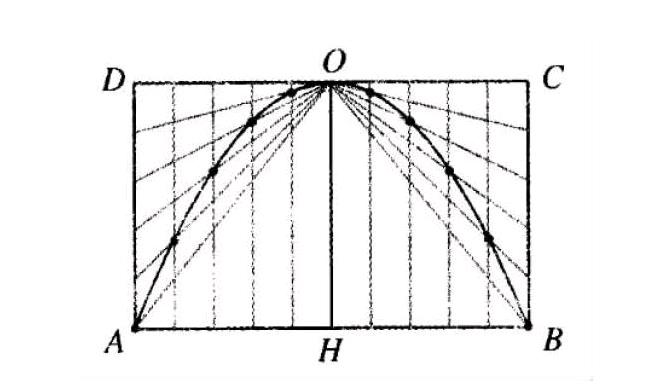
你能说出上述画法的正确性吗?
总之,用研究性学习的方式开展课堂教学是符合学生学习规律的,研究性学习模式远比传统的课堂模式复杂,需要更全面的思考与准备,过程一定是“精细化”的。从效果上看这一节课学生对定义、方程及探索过程中的学习体验都是比较到位的,留下了较深的“数学思想方法,和切身体会的活动过程感受”,对学生的启发较大,今后我还会不断探究“研究性学习”的课堂模式,将研究性学习开展得更好。
