基于小波分析的虚拟电网谐波检测系统的研究

卓书芳，何用辉，郑　昕

(1.福建信息职业技术学院机电工程系，福建 福州 350003；

2.福州大学电气工程与自动化学院，福建 福州 350002)



基于小波分析的虚拟电网谐波检测系统的研究

卓书芳1，何用辉1，郑昕2

(1.福建信息职业技术学院机电工程系，福建 福州 350003；

2.福州大学电气工程与自动化学院，福建 福州 350002)

摘要：为提高虚拟电网谐波治理的水平，将小波分析应用于虚拟电网的谐波检测中.分析了小波分析和虚拟电网的基本原理.然后，设计了基于Morlet小波的虚拟电网检测算法，并进行了虚拟电网谐波检测的仿真.仿真结果表明，小波分析是一种切实可行的虚拟电网谐波检测方法.

关键词：小波分析；虚拟电网；谐波检测

目前，电力系统谐波污染越来越严重，电网系统的非线性负荷一方面将形成稳态谐波，另外一方面还形成暂态谐波，经常出现电网的电压和电流波形的畸变现象，严重地干扰着电力系统的稳定运行，对电网系统的用户不利.谐波一方面影响着用户和终端设备，另外一方面还增加了线路的损耗，降低了线路的传输性能，对通讯信号产生影响.为了能够较好地降低谐波的污染，促进电气环境的提升，有必要对电网系统的谐波参数进行精准地检测，从而能够提高电网系统的谐波治理水平[1].目前，电网系统谐波治理方法有许多，最为常见的就是傅立叶变换.然而电网系统的负载处于动态变化之中，电网系统的电压和电流波形产生动态的波动，而傅立叶变换仅在处理平稳信号具有较大的优势，因此，无法满足电网系统谐波治理的需求.为了能够提高虚拟电网系统谐波治理的水平，需要一种有效的方法对电网系统谐波进行检测.小波分析能够较好地实现信号去噪，通过小波系数实现阈值处理，从而能够消除谐波中的噪声，进而避免噪声的干扰.小波分析能够消除信号中大部分的噪声，避免了干扰信号的能量和其他频谱混合，从而能够较好地提升频域分析的精度，此外还能够有效地测量各次谐波的含有率.因此，将连续小波分析应用于电网谐波检测中是切实可行的.

1小波分析的基本原理

1.1小波分析的数学模型

定义小波函数的表达式为φ(t)∈L2(R)，然后对φ(t)采取相应的调整，调整方程为φi(t)=φi(t-i)，i∈Z，可以获得如下的公式[2]：

(1)

此时，φ(t)表示尺度函数，能够在L2(R)张成尺度空间V0，可以表示为如下的形式：

V0=span{φi(t)}

(2)

尺度函数集可以通过对尺度函数进行平移与伸缩操作来构造，对应的表达式如下所示：

(3)

V0对应于尺度i=0，如果尺度i≠0，尺度i上的尺度空间能够利用如下的数学模型来描述：

(4)

定义某一信号的函数为f(t)，对应的小波变换能够利用如下的模型来描述：

(5)

由于虚拟电网谐波检测过程具有较强的非线性特点，因此，能够通过具有多分辨分析特征的小波分析技术对虚拟电网谐波进行检测，并且设计出相应的检测系统.

1.2小波分析的多分辨分析

已知一信号函数为f(t)，其小波变换的数学模型如下所示：

(6)

尺度函数能够构造成相应的尺度空间，当尺度持续增加时，尺度函数平移的间隔将相应地提高.否则，张成的尺度空间可以使信号的细节更加明确.所以，尺度的改变能够使信号分析的精度高低随之而变，换言之，就是小波分析具备多分辨分析的特点，能够表示为如下的形式[3]：

V0=V1⊗W1=V2⊗W2⊗W1=…

(7)

式中，W1为细节空间；V1为大尺度的逼近空间.在信号分析的过程能够依据实际状况，实现对尺度空间的分解，进而能够得到相应的细节信号与尺度信号.

1.3小波函数的选择

Morlet小波的频域能量相对集中，通频带也比较窄，频率混叠的干扰不大，同时具备线性相位和时域对称的优点，可以确保变换不会出现失真现象.因此，Morlet小波应用于虚拟电网谐波检测中是切实可行的，Morlet小波的数学模型为：

(8)

2虚拟电网的基本原理

虚拟电网主要包括输入模块、能量转换模块、输出模块、检测与控制模块.输入模块和输出模块包括不同类型的电磁开关与EMI滤波器，能够控制电路的通断，并且能够防止电磁的负面影响.能量转换模块利用不同的转换技术把输入的电网电压转换为交流电压，该交流电压的幅度可变、频率可变，同时包含高次谐波，对电网的故障进行模拟，该模块为虚拟电网的核心.检测和控制模块能够控制模拟器形成必要的电压波形，并且能够对电路中的电气参数和模拟器的程序进行控制.

其中，能量转换模块包括整流电路和逆变电路.前者的功能是把输入模拟器的电网电压转换为直流电，能够为逆变环节提供稳定的直流电压.后者的功能是将整流过程中形成的直流电压转换为交流电压，从而能够更好地模拟电网电压的正常状况与不同故障下的功能.

虚拟电网的模拟器主要是由三个相互独立的单相子电路构成的，不同相的输出能够模拟电网电压的一相.不同的子电路采用了交-直-交的架构，不同的子电路的架构包括整流和逆变电路.整流电路利用三相PWM结构，可以把输入的交流电转换为直流电，输出侧易于形成稳压.三相整流电路可以使有源负荷形成的能量返回至电网，从而实现能量的双向流动.逆变环节利用PWM结构，可以得到交流电压.逆变器包含大量的高次谐波，所以，应该利用LC滤波器去除高次谐波.

3基于Morlet小波的虚拟电网检测算法

为了降低混频现象发生的概率，选择连续积分小波变换，尺度系数分别取1，2，3，….因此，尽管尺度不同时混频现象仍然存在，然而多尺度的小波变换能够使变换谱图更加明显，所以能够用于检测虚拟电网的谐波.小波变换的基本原理就是将信号中的局部能量特征提取出来，正弦波的波形在不同的周期内包含两个能量极大值，所以能够依据此特征判别采样数据中的谐波特征.此外，由于Morlet小波在时域内具有对称性的特点，同时属于线性相位，因此能够确保小波变换不失真，能够通过特征尺度的重构信号对虚拟电网的谐波特征进行分析.

虚拟电网系统中最常见的噪声类型就是具有叠加性的高斯白噪声，信号在高斯白噪声的影响下所对应的数学模型如下所示[4]：

di=fi+ε·zi

(9)

式中，di表示包含高斯白噪声的信号，fi表示原始信号，zi表示独立同分布的高斯白噪声信号N(0,1)，ε表示噪声水平.

从包含高斯白噪声的信号di中将原始信号fi还原出来，主要通过利用小波变换下的不同特征，利用小波分解系数实现信号和噪声的分离.在应用中，有价值的信号一般以低频信号或平稳信号的形式存在，噪声信号一般以高频信号的形式存在，因此，首先应该对包含高斯白噪声的信号进行小波分解，相应的表达式如下所示：

S=cA1+cD1=cA2+cD2+cD1=cA3+cD3+cD2+cD1

(10)

式中，cAi表示小波分解的近似项，cDi表示小波分解的精细项，i=1,2,3,….高斯白噪声一般情况包含在cDi(i=1,2,3,…)中，去噪过程的基本步骤如下所示[5]：

步骤1：虚拟电网谐波信号的小波分解

分解方程如下所示：

W0d=W0f+ε·W0z

(11)

式中，d表示虚拟电网谐波信号向量d1,d2,…,dN，f表示失真信号向量f1,f2,…,fN，z表示高斯向量z1,z2,…,zN.

步骤2：对小波系数W0d进行临界值处理，相应的表达式如下所示：

(12)

临界值处理的表达形式为ηtNW0d，当N→∞时，利用上述临界值对小波因子进行处理能够去除虚拟电网谐波信号中的噪声.

步骤3：通过对分解后的小波因子进行逆变换来实现信号的重构

(13)

最终能够获得去噪之后的虚拟电网谐波信号.

4虚拟电网谐波检测的仿真分析

为了验证Morlet小波分析在虚拟电网谐波检测中的有效性，利用Morlet小波对虚拟电网谐波进行检测，虚拟电网系统的谐波信号如下所示：

x(t)=0.2sin(ω0t+π/5)+0.3sin(2ω0t+π/10)+0.4sin(4ω0t+π/4)

+0.25sin(6ω0t+π/3)+0.25sin(8ω0t+2π/5)+0.1sin(9ω0t+π/6)

构造一个SNR=45db的随机高斯白噪声，利用Morlet小波对含噪声的虚拟电网谐波信号进行处理，并且计算出各次谐波的含有率和总谐波的畸变率.计算结果见表1.

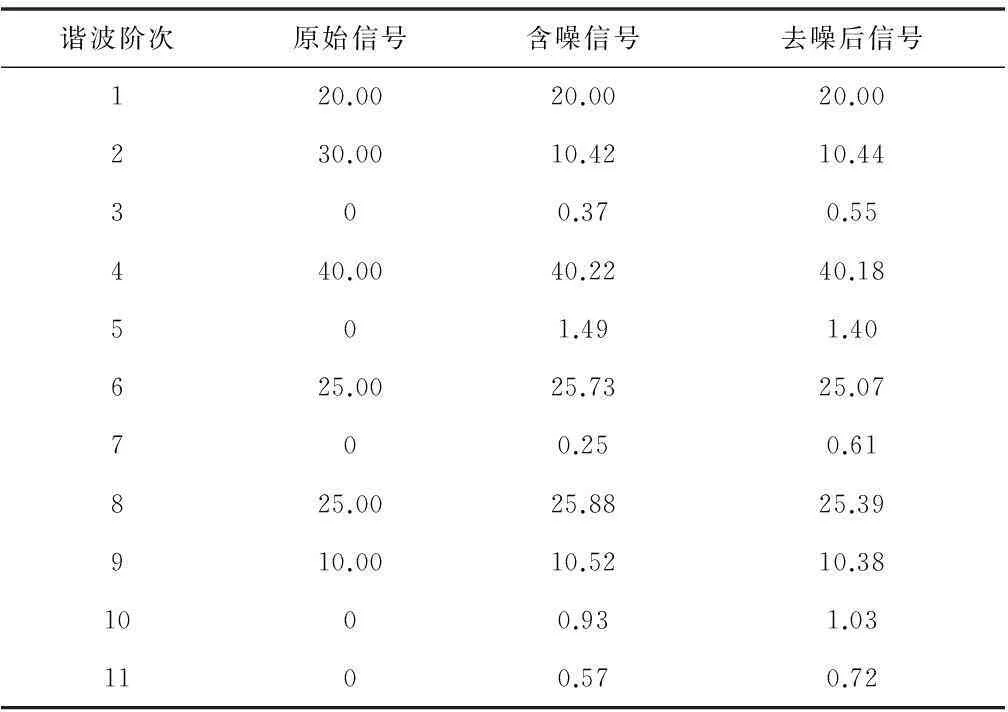
表1　谐波去噪后的虚拟电网信号的谐波含有率

从表1的计算结果可以看出，经过小波去噪后的虚拟电网各次谐波的畸变率和原始信号较为接近，能够较好地体现各次谐波含有率，从而能够提高虚拟电网谐波污染的治理水平.

此外，假设虚拟电网系统在t=0.02s时出现故障，故障前后信号的幅值与相角见表2.

表2　虚拟电网系统故障前后的幅值与相角

以虚拟电网故障信号为例，加入随机噪声，均值为0，方差为0.04，利用Morlet小波对其进行6个尺度的分解.分解和误差计算结果见表3和表4.

表3　虚拟电网故障前幅值、相角的分解和误差计算结果

从表3和表4的计算结果可以看出，整个检测过程中，幅值和相角的误差均控制在2%之内.当采样频率增加、变换尺度提高时，误差将随之减小；同时，计算量随之提高，所以在实际应用的过程中，应该选择合适的采样频率和尺度.

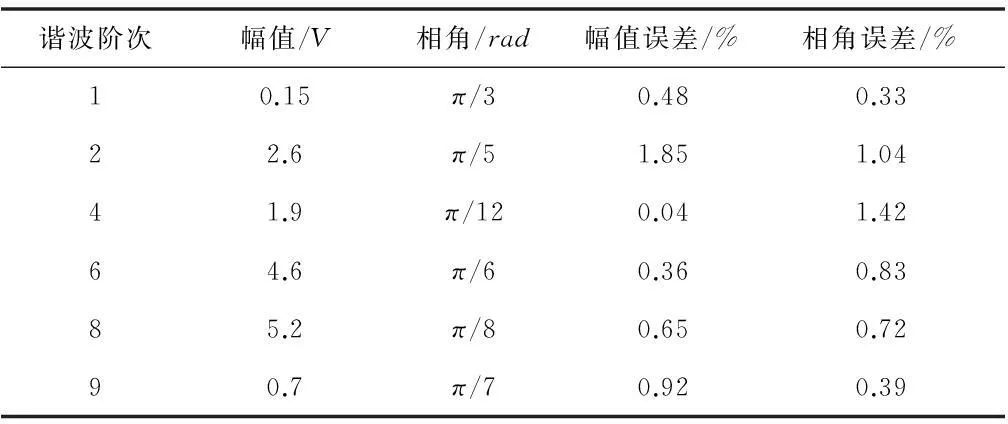
表4　虚拟电网故障后幅值、相角的分解和误差计算结果

5结论

将小波分析应用于虚拟电网谐波的检测系统中，对虚拟电网故障后的谐波进行检测，能够推算出故障信号的幅值和相角.算例分析表明，小波分析在虚拟电网谐波检测中具有较好的实用性.

参考文献：

[1] 吴轩钦, 谭国俊, 张倩倩, 等. 新颖虚拟电网磁链在有源滤波器中的应用[J]. 电力系统及其自动化学报, 2010, (6):77-82.

[2] 王晴晴, 黄友锐, 陈珍萍, 等. 基于改进阈值去噪的谐波检测电测与仪表[J]. 电测与仪表, 2015, (13):20-24.

[3] 罗冠姗, 卢惠辉, 苏成悦, 等. 一种基于小波包变换的电力谐波检测方法[J].电力建设, 2015, (3):71-76.

[4] 陈吉, 商红桃. 小波包变换及其在电力系统谐波电流检测中的应用[J]. 现代电子技术, 2015, (5):62-63.

[5] 陈勇, 田丽, 赵明敏, 等. 基于滑窗迭代DFT和小波包分析的谐波电流检测方法[J]. 重庆工商大学学报：自然科学版, 2014, (11):35-39.

(责任编校：晴川)

Harmonic Detection System Based on Wavelet Analysis

ZHUO Shufang1, HE Yonghui1, ZHENG Xin2

(1. Department of Mechatronics Engineering, Fujian Polytechnic of Information Technology,Fuzhou Fujian 350003, China;2. College of Electrical Engineering and Automation, Fuzhou University, Fuzhou Fujian 350002, China)

Abstract：In order to improve the level of harmonic control in virtual network, the wavelet analysis is applied to the harmonic detection in the virtual network. Firstly, the basic principle of wavelet analysis and virtual network is analyzed. Then, the virtual network detection algorithm based on Morlet wavelet is designed, and the simulation of harmonic detection in virtual network is conducted. Finally, the simulation results show that the wavelet analysis is a feasible method for harmonic detection in virtual network.

Key Words：wavelet analysis; virtual network; harmonic detection

中图分类号:TP216

文献标识码：A

文章编号：1008-4681(2016)02-0047-03

作者简介：卓书芳(1976— )，女，福建屏南人，福建信息职业技术学院机电工程系讲师，硕士.研究方向：机电系统辨识与智能控制.

基金项目：2013年福州市科技计划项目“基于物联网的分布式直流电力操作电源系统研制”(批准号：2013-G-95)；2015年福建省中青年教师教育科研项目“虚拟仪器技术在电网谐波检测中的应用研究”(批准号：JA15680).

收稿日期：2016-01-23