基于遗传膜算法的含风电机组和电动汽车的配电网分时段动态重构

吴泓俭雷 霞刘 斌芦 杨徐贵阳

（1.西华大学电力电子节能技术与装备重点实验室 成都 610039 2.国网达州供电公司 达州 635000 3.福建省电力有限公司南平电业局 南平 353000）



基于遗传膜算法的含风电机组和电动汽车的配电网分时段动态重构

吴泓俭1,2雷 霞1刘 斌3芦 杨1徐贵阳1

（1.西华大学电力电子节能技术与装备重点实验室 成都 610039 2.国网达州供电公司 达州 635000 3.福建省电力有限公司南平电业局 南平 353000）

摘要在新能源不断接入配电网的环境下，配电网分时段动态重构变得越来越重要。配电网分时段动态重构模型中考虑了电力公司从风电机组的购电成本、随机波动性成本、电动汽车充放电成本和网络损耗成本等。在满足各时段配电网安全运行等约束条件下，以配网经济性最优为目标函数确定最终的开关组合，该模型反映了风电机组和不同类型电动汽车对电网经济性的影响。为克服重构中产生大量重复解，提出等份交叉概率选择法，并提出一种膜计算与改进遗传算法相结合的遗传膜算法对上述模型进行求解，该算法克服了基本遗传算法的“早熟”问题。实验验证了上述模型和方法的正确性和有效性。

关键词：动态重构 风电机组 不同类型电动汽车 等份交叉概率选择法 遗传膜算法

四川省教育厅重点项目（11za002），成都市科技局软科学项目（12RKYB192ZF-002），西华大学创新基金（ycjj2014078）和电力电子节能技术与装备重点实验室开放基金（szjj2014-015）资助项目。

0 引言

近年来，随着国家经济不断发展，同时面临化石能源的日益枯竭，世界各国都在大力研究清洁能源技术，以缓解日益严重的能源危机。在此背景下，风电机组和电动汽车得到了越来越广泛的应用[1,2]。风电机组的出力和电动汽车的充放电都具有较强的随机性和波动性，大规模的风电机组和电动汽车接入电网给配电网的优化运行与管理带来新的挑战。

配电网重构在本质上是一个离散、非线性组合优化问题，其主要目的在于满足降低配电网网损、均衡负荷和提高供电电能质量等相关指标下，通过改变线路开关的组合状态，寻找到一组最优或次优的配电网开关组合。对于配电网重构问题，国内外学者已提出相关的解决方法[3-7]。文献[8,9]提出了针对负荷变化的动态重构方法。文献[10]在电力市场环境下建立了含分布式电源的配电网重构模型。文献[11]针对含分布式电源的配电网重构提出了改进蜜蜂进化型遗传算法。文献[12]建立了计及入网电动汽车和分布式电源的配电系统重构模型，其切入点是从充电策略方面考虑电动汽车充放电对配网重构的影响，而实际中，对于不同类型的电动汽车，其运行的规律及对电网的影响不尽相同。以上研究存在以下三点不足：①大多数研究局限于传统的静态重构，这显然不能满足含分布式电源的配电网重构实际要求；②很少有文献充分考虑分布式电源的随机波动性和不同类型电动汽车随机充放电行为对配电网重构的影响；③所采用的优化方法易陷入“早熟”的困境。

在此背景下，本文以最小化从风电机组处的购电成本、随机波动性成本、不同类型电动汽车的随机充放电成本以及网络损耗成本之和为目标函数建立动态重构模型。以一天为周期，分析不同类型电动汽车的充放电时段，根据电动汽车类型、起始荷电状态、充放电需求和起始充放电时间计算，获得充放电负荷曲线，然后综合考虑相应时段风电出力曲线，最后采用所提膜计算与改进遗传算法相结合的遗传膜算法对所建模型进行优化。

1 计及风电机组和电动汽车配电网的重构模型

1.1 目标函数

本文以一天为周期，从电网的角度分析了从风电机组处的购电成本、随机波动性成本、电动汽车随机充放电成本和网络损耗成本，并最终寻求满足支路容量、节点电压和辐射运行等约束条件的经济性最优或次优重构方案。配电网重构问题的数学模型为

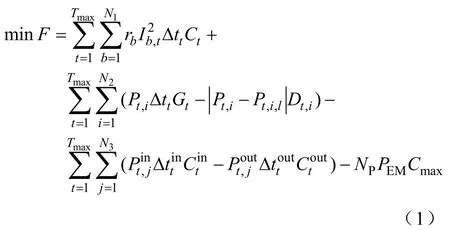
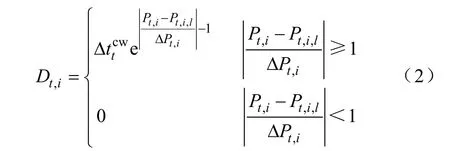
1.2 约束条件

（1）对每时段的配电网结构，需满足潮流约束[2]。

（2）辐射状网络运行和无孤岛约束。配电网正常运行时，必须辐射状运行且每个节点必须连通。

（3）节点电压约束

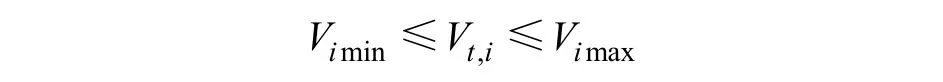
式中，Vt,i为节点i在t时段的电压幅值；分别为节点i电压幅值的下、上限。

（4）支路电流约束

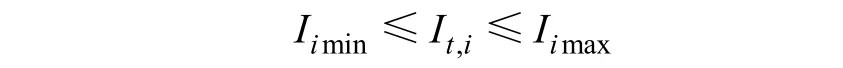
式中，It,i为节点i在t时段的电流幅值；分别为节点i电流幅值的下、上限。

（5）开关约束。为延长开关寿命，本文对单个开关操作次数及总的开关操作次数做相应地限制。

2 不确定性因素模拟

2.1 风电机组

风电机组的发电计划主要取决于当地风速，假设风速随机变量v服从w（ k,c）表示的Weibull分布，则风电机组输出功率Pw随风速变化的关系[13]为

式中，vc为切入风速；vco为切出风速；vr为额定风速；Prated为风力发电机的额定输出功率。

2.2 不同类型电动汽车

文献[14]已对电动汽车的充电行为有了详细介绍，本文在此基础上进一步分析不同类型电动汽车的放电和换电池行为，最后采用蒙特卡洛法得到不同类型电动汽车的充放电负荷曲线。此处采用快速放电方式，则不同类型电动汽车的放电和换电池模式如下：

（1）公交车、出租车：称为第一类电动汽车，该类汽车作为一种大众交通工具，一天中大部分时间处于交通运输阶段，其运行机制为分批次轮班倒。公交车早上5∶30开始运行，每辆车发车间隔时长通常为3～10min，通常22∶00点收车；出租车因无固定路线约束，运行相对自由，根据乘客出行规律可将出租车运行分为白班和晚班2种模式，白班通常在11∶30～15∶00期间乘客人数较少，可对其进行快速充电；晚班通常在2∶00～5∶00乘客较少，可对其进行常规充电。为保证该类车第二天的良好运营，需对其进行有计划的充电，因此该类车不加入放电和换电池模式群体。

（2）公务车：称为第二类电动汽车，该类车通常在上、下班时段运行，其空闲时间相对较多，有足够的充电时间，可加入放电模式群体。在分段电价情况下，为进一步考虑车主利益，服务地区电网优化运行，假设该类车充电时段为白天15∶00～18∶00，夜间23∶00～7∶00；放电时段为白天10∶00～13∶00，夜间20∶00～23∶00，起始放电SOC满足正态分布N（0.8，0.12）。由于该类车的充电时段充裕，因此不加入换电池模式群体中。

（3）私家车：称为第三类电动汽车，该类车运行随机性最大，但其大部分时间都停放在办公停车场或居民停车场，业余时间可能停放在商场、超市等专用或公共停车场。因此其充电时段大致可分为以下3个时段，白天为9∶00～17∶00或15∶00～18∶00，夜间为23∶00～7∶00。对于放电行为，该类车只有在保证车主一天的行程基本上，才能加入放电群体，且考虑到一天中的未知计划，该类车的放电时段大多集中在晚上高峰段，即为20∶30～22∶00，起始放电SOC满足正态分布N（0.6，0.12）。因该类车的随机性很大，需加入换电池模式群体中，假设一天中最易换电池的时间段为11∶30～13∶00和15∶00～18∶00，且需要换电池的车辆为该类车的3%～5%。

综上所述，基于蒙特卡洛模拟不同类型电动汽车充放电负荷曲线的流程如图1所示。

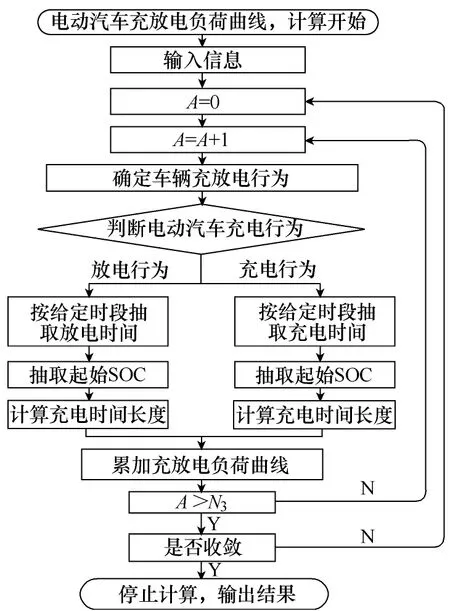
图1　基于蒙特卡洛模拟的不同类型电动汽车充放电负荷曲流程Fig.1 Flow chart of different kinds of electric vehicle charging and discharging load curve based on Monte Carlo simulation

3 基于遗传膜计算含分布式电源的配电网分时段动态重构

为充分利用遗传算法[15]易得到全局最优解的优点，文章结合膜计算[16-19]理论以及膜计算的运行优点，将遗传算法引入到膜计算当中，并称这种算法为遗传膜算法。

3.1 遗传膜计算的原理

在遗传膜计算中，每个对象代表一个解。文中构建的遗传膜算法结构如图2所示，采用一个度为8的膜系统，多元组表示为

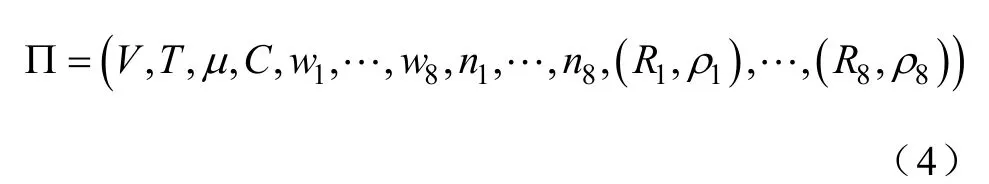
图2　遗传膜计算膜结构Fig.2 Membrane structure of GMA

3.1.1 编码规则

在重构问题中，由于开关只有开、关两种状态，因此常采用二进制编码，但二进制编码会增加对象的长度，同时在随机生成解的过程中易产生重复解，这将大大降低算法的效率。因此，在遗传膜算法中，采用支路号编码。

3.1.2 对象

每个膜中的对象集表示为

为解决在随机生成解中易产生重复解这一问题，此处先通过对网络进行简化[20]，然后对简化后的支路组及支路采用等份交叉概率选择法进行选择，具体做法如下。图3表示的是IEEE 33节点网络[10]简化图。

图3　IEEE 33节点网络简化图Fig.3 Simplified diagram of 33 nodes

在图3中，为使网络呈辐射状，需要分别在环路Ⅰ、Ⅱ、Ⅲ、Ⅳ和Ⅴ对应的支路组中断开一条支路，且每个支路组最多只能断开一条支路。支路组由无数支路组成，因此对支路组中支路进行随机选择时，需使每条支路被选择的概率均等。本文提出等份交叉概率选择法的思路如下：假设一条支路组由n条支路组成，每条支路被选择的概率区间总长度为1/n。将每个区间长度1/n分成n等份，则最小概率区间长度为1/n2。某一条支路被选择的概率范围由从n条支路中依次选择出来的最小区间范围组成。则支路组R下第k条支路的等份交叉概率选择区间范围可表示为

图3中，支路组2包含3条支路，分别为18、19和20，则支路组2中每条支路的等份交叉概率选择区间范围如图4所示。

图4　等份交叉概率选择区间范围Fig.4 Equal sections crossover probability selection method

图4中每个表格代表一个最小概率区间长度，其值为1/9，则

3.1.3 进化规则

在每次迭代中，每个膜将本区域中最好的几个对象传送到区域外，同时将区域外最好的几个对象传送到区域内，这实现了膜与膜之间的交换，增强了膜间的交流，提高了膜计算的效率。膜间交流规则表示为

3.1.4 交叉、基本膜分裂规则

类似遗传算法的交叉操作，通过交叉率选择出需要参与交叉规则的对象p1、p2，再随机选择交叉部分进行交叉，得到新对象，最后用新对象代替基本膜内的最差对象，同时基本膜分裂，以扩大其搜索范围。

交叉、基本膜分裂规则表示为

式中，p1、p2表示区域i内参与交叉规则的对象；表示区域i内参与交叉规则后的新对象；pmax为区域i内的最差对象；表示膜的极性，初始膜极性为中性；表示对象中的第i位；其中pos1，pos2∈[1,d]分别表示对象中的第pos1，pos2位。

3.1.5 变异、消融规则

为提高算法搜索全局最优解的能力，此处选取最差对象参与变异规则，最后将非中性膜消融，此时非中性膜内的对象进入外围区域中。变异、膜消融规则表示为

式中，pmax、p5分别为区域i内的参与变异规则前的对象和变异后的对象；ptotal、p分别为区域i内的全部对象以及与外围区域不同的对象。

3.2 基于遗传膜计算配电网分时段动态重构流程图

风电机组和电动汽车加入配电网后，必然影响一天的负荷曲线，同时在一天的不同时段，负荷水平会因为不同类型电动汽车所接比例而存在较大差异。因此为了使网络运行的经济性最大化，需要根据不同类型电动汽车接入电网的比例，对负荷变化较大的时段进行合理的动态开关重构[8,9]。基于遗传膜计算的配电网分时动态重构流程图如图5所示。

图5　基于遗传膜算法的配电网分时段动态重构流程Fig.5 Flow chart of dynamic reconfiguration of distribution network with dividing time based on GMA

4 算例分析

本文以修改过的IEEE 33节点系统进行算例分析。风电机组和电动汽车分别接入节点7、24，具体参数如下：

（1）风电机组额定功率Prated＝1MW，切入风速vc＝4m/s，切出风速vco＝25m/s，额定风速vr＝14m/s，本文接入10台风电机组。一天中的风速信息见表1，惩罚值与偏差冗度及偏差持续时间的关系如图6所示。

表1　风速信息Tab.1 Wind speed information

图6　不同持续时间下的惩罚值曲线Fig.6 Penalty value curves at different duration

由图6可知，当偏离冗度一定时，持续时间越长，惩罚值越大；当持续时间一定时，偏离冗度越大，惩罚值越大。这表明，风电机组随机波动性越大，持续时间越长，对电网的危害性就越大，因此对风电机组的惩罚就越厉害。

（2）根据2.2节不同类型电动汽车对电网影响的分析，结合汽车普及规律将第一类、第二类和第三类电动汽车接入电网的比例分为以下两种情景来分析其对电网动态重构的影响。第一种情景为电动汽车示范运营阶段，接入比例为6∶3∶1；第二种情景为电动汽车普及阶段，接入比例为2∶3∶5。假设充电站在第一种情景下投入100辆电动汽车，在第二种情景下已投入400辆电动汽车。充电功率依照国家标准，以BYD E6为参考，出租车所使用的电池额定电压为320V、额定容量200A·h，其常规、快速充电功率为14kW和90kW。公务车、私家车所使用的电池额定电压为320V、额定容量100A·h，其常规、快速充电功率为7kW和45kW，放电功率为14kW，假设公家车充电功率为私家车的3倍。

电动汽车充放电负荷预测参数设置[14]见表2。采用Monte Carlo模拟电动汽车站的充放电负荷如图7所示，各时段对应的电价信息如图8所示。

（3）随着电动汽车的不断普及，大量新能源接入配电网，使得风电不断发展。假设在电动汽车普及阶段，为分析风电接入对配电网的影响，结合文中案例，对风电机组接入电网的初期、中期和后期三种场景进行测试，各场景接入风电机组分别为5台、10台和15台。

（4）本文对于动态重构中的时间划分采用文献[8,9]中相关技术，并设定单个开关操作次数不大于2次，总开关操作次数不大于16次，重构时段数不大于3，相邻时段间单次开关操作的费用下降阈值为0.08万元。

表2　电动汽车充放电负荷预测参数设置Tab.2 Parameter settings for charging and discharging load prediction

图7　不同充放电行为下的等效负荷曲线Fig.7 Equivalent load curve under different charge/discharge behavior

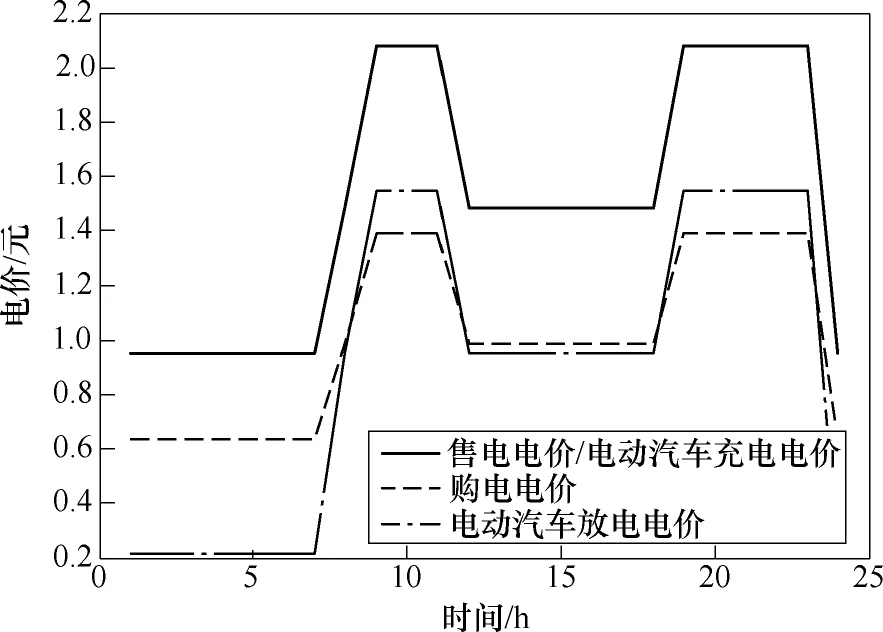
图8　电价曲线Fig.8 Price curve

采用所提遗传膜算法对计及风电机组和电动汽车的配电网络进行动态重构，并将所得结果与遗传算法所得结果进行比较。

由表3～表6的结果可以得到，一方面新方法在满足配网动态重构相同约束的条件下，能够得到比传统遗传算法更好的重构结果，且总的开关次数有所减少，避免了不必要的开关操作，从而在一定程度上降低了开关操作成本；另一方面随着电动汽车的不断普及，大量用电用户接入电网，将使得电网成本随之下降，有利于电网的可持续发展。

表3　遗传算法对情景一优化结果Tab.3 GA optimization results for scenario one

表4　遗传膜算法对情景一优化结果Tab.4 GMA optimization results for scenario one

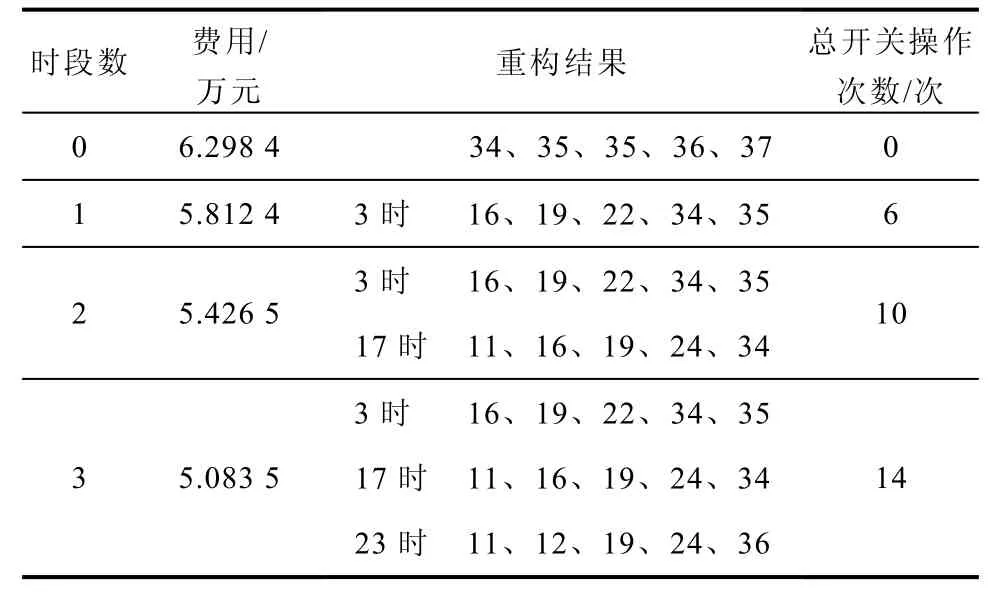
表5　遗传算法对情景二优化结果Tab.5 GA optimization results for scenario two

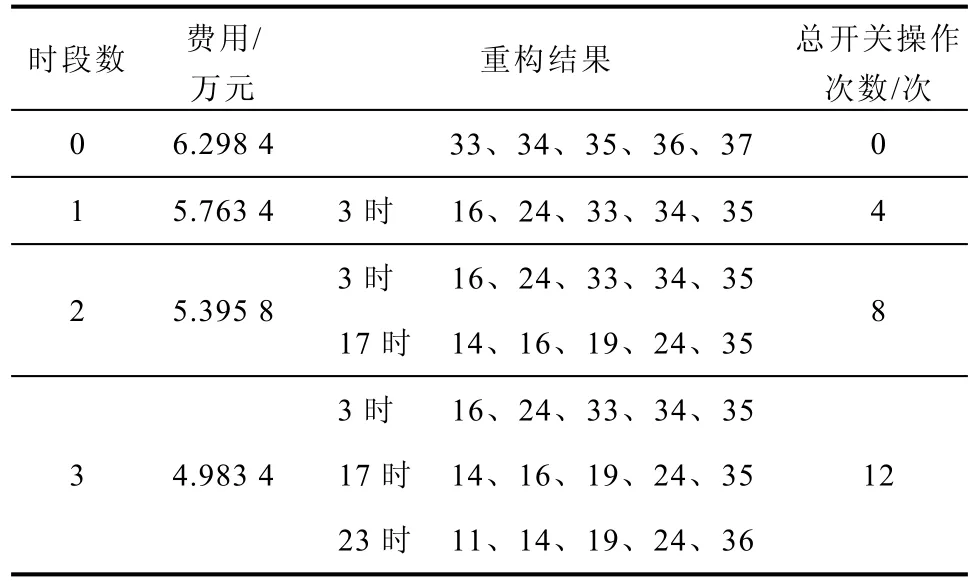
表6　遗传膜算法对情景二优化结果Tab.6 GMA optimization results for scenario two

由表3～表6所示的配电网动态重构方案可得到不同情景下不同算法各时段的最低节点电压图，如图9、图10所示。从图中可得到：①在新建立的模型下，采用文中所提算法得到的解能够有效提升系统的最低电压，从而提高供电可靠性；②对比图9、图10可得，随着电动汽车的不断普及，通过合理的开关操作，可提高电网节点电压水平。原因在于，在示范阶段，第二、三类电动汽车数量较少，不能起到削峰作用，而在普及阶段，第二、三类电动汽车数量大量增加，在负荷高峰时段，可大量向电网供电，起到削峰作用，因此电压水平较高。

图9　情景一最低节点电压Fig.9 The lowest node voltages for scenario one

图10　情景二最低节点电压Fig.10 The lowest node voltages for scenario two

为分析风电对配网的影响，在电动汽车普及阶段，结合文中案例，对风电接入电网的初期、中期和末期进行测试，且各期接入风机的数量分别为5台、10台和15台。同时为验证文中所提算法的有效性，本文采用两种算法对风电接入配网的各时期进行优化，其优化结果如上表所示。需特别说明，表5、表6不但表示电动汽车接入配网的情景二优化结果，同时也表示风机接入电网的中期优化结果。

对比各时期优化结果的两表可得，在相同条件下，遗传膜算法寻优结果比遗传算法寻优结果较好，且开关操作次数也有所减少；对比各时期的遗传膜算法优化结果可得，随着风电接入电网的比例不断增加，电网的成本费用也随之增加。且同等比例的风电接入电网时，末期投入时电网增加的费用比中期投入时电网增加的费用高。主要原因在于，随着风电的接入，风力发电功率增大到一定值后，其对配网的影响范围也迅速扩大，此时将增大有功功率和无功功率的非同向流动，从而导致配网网损增大，成本费用增加。

由表5～表10可得到风电接入配网各时期下不同算法各时段的最低节点电压图。需特别说明，图10不但表示电动汽车接入电网的情景二最低节点电压，同时也表示风电接入中期最低节点电压。

从图10～图12中可得到：①在新建立的模型下，采用文中所提算法得到的解能有效优化系统的最低电压，从而提高供电可靠性；②对比图10～图12可得，风电接入配网能够提高配网网络节点电压水平，且随着风电接入配网的比例不断增加，配网节点电压水平逐渐提高，但当接入配网的风电功率达到一定值后，会使得配网节点电压水平超过其额定值，以致破环配网安全运行，使得配网运行可靠性降低。

表7　遗传算法对风电接入初期优化结果Tab.7 GA optimization results for wind power integration in the initial stage

表8　遗传膜算法对风电接入初期优化结果Tab.8 GMA optimization results for wind power integration in the initial stage

表9　遗传算法对风电接入末期优化结果Tab.9 GA optimization results for wind power integration at the end of period

表10　遗传膜算法对风电接入末期优化结果Tab.10 GMA optimization results for wind power integration at the end of period

图11　风电接入初期最低节点电压Fig.11 The lowest node voltages for wind power integration in the initial stage

图12　风电接入末期最低节点电压Fig.12 The lowest node voltages for wind power integration at the end of Period

5 结论

针对风电机组和不同类型电动汽车充放电的随机波动性，本文分别提出偏离冗度惩罚和不同类型电动汽车随机充放电行为模拟方法，并最终建立了计及风电机组和不同类型电动汽车分时段动态重构新模型。

文章在提出遗传膜算法的基础上，针对重构中产生大量重复解这一问题，通过对配电网络进行结构简化，提出等份交叉概率选择法以提高随机解选择准确度，避免产生大量重复解。

采用所提遗传膜算法求解所建立的新模型，并将所得仿真结果与传统遗传算法进行比较，结果表明，所提出的配电网络分时段动态重构模型和遗传膜算法，能够有效实现计及风电机组和不同类型电动汽车的配电网络分时段动态重构，提高供电可靠性等。

参考文献

[1]Peng F Z.Editorial special issue on distributed power generation[J].IEEE Transactions on Power Electronics,2004,19（5）:1157-1158.

[2]刘志鹏,文福拴,薛禹胜,等.计及可入网电动汽车的分布式电源的最优选址和定容[J].电力系统自动化,2011,35（18）:11-16.Liu Zhipeng,Wen Fushuan,Xue Yusheng,et al.Optimal siting and sizing of distributed generators considering plug-in electric vehicles[J].Automation of Electric Power Systems,2011,35（18）:11-16.

[3]张栋,张刘春,傅正财.配电网络重构的快速支路交换法[J].电网技术,2005,29（9）:82-88.Zhang Dong,Zhang Liuchun,Fu Zhengcai.A quick branch-exchange algorithm for reconfiguration of distribution networks[J].Power System Technology,2005,29（9）:82-88.

[4]靳晓凌,赵建国.基于改进二进制粒子群优化算法的负荷均衡化配电网重构[J].电网技术,2005,29（23）:41-43.Jin Xiaoling,Zhao Jianguo.Distribution network reconfiguration for load balancing based on improved binary particle swarm optimization[J].Power System Technology,2005,29（23）:41-43.

[5]张浩,和敬涵,薄志谦,等.基于动态规划算法的故障恢复重构[J].电工技术学报,2011,26（12）:162-167.Zhang Hao,He Jinghan,Bo Zhiqian,et al.Service restoration based on dynamic programming[J].Transactions of China Electrotechnical Society,2011,26（12）:162-167.

[6]Niknam T.An efficient multi-objective HBMO algorithm for distribution feeder reconfiguration[J].Expert Systems with Applications,2011,38（3）:2878-2887.

[7]Abdelaziz A,Mohamed F,Mekhamer S,et al.Distribution system reconfiguration using a modified tabu search algorithm[J].Electric Power Systems Research,2010,80（8）:943-953.

[8]刘健,徐精求,董海鹏.考虑负荷变化的配电网动态优化[J].继电器,2004,32（13）:15-19.Liu Jian,Xu Jingqiu,Dong Haipeng.Distribution networks dynamic optimization considering load changes[J].Relay,2004,32（13）:15-19.

[9]余建明,王征,许苗.考虑负荷变化的配电网动态分时段重构[J].高电压技术,2007,33（9）:125-128.Yu Jianming,Wang Zheng,Xu Miao.Dynamic reconfiguration of distribution network with dividing time and considering load changes[J].High Voltage Engineering,2007,33（9）:125-128.

[10]卞栋,卫志农,黄向前,等.电力市场中含分布式电源的配电网重构模型[J].电力系统保护与控制,2013,41（11）:117-123.Bian Dong,Wei Zhinong,Huang Xiangqian,et al.Distributed network reconfiguration model including distributed generation in the electricity market[J].Power System Protection and Control,2013,41（11）:117-123.

[11]王超学,吕志奇,董慧,等.基于改进蜜蜂进化遗传算法的含分布式电源的配电网重构[J].电力系统保护与控制,2012,40（15）:53-56.Wang Chaoxue,Lü Zhiqi,Dong Hui,et al.Distribution network reconfiguration with distributed generation based on an improved bee evolutionary genetic algorithm[J].Power System Protection and Control,2012,40（15）:53-56.

[12]陈光,戴攀,周浩,等.计及入网电动汽车和分布

式电源的配电系统重构[J].电网技术,2013,37（1）:82-88.

Chen Guang,Dai Pan,Zhou Hao,et al.Distribution system reconfiguration considering distributed generators and plug-in electric vehicles[J].Power System Technology,2013,37（1）:82-88.

[13]张节潭,程浩忠,姚良忠,等.分布式风电源选择

定容规划研究[J].中国电机工程学报,2009,29（16）:1-7.Zhang Jietan,Chen Haozhong,Yao Liangzhong,et al.Study on siting and sizing of distributed wind generation[J].Proceedings of the CSEE,2009,29（16）:1-7.[14]罗卓伟,胡泽春,宋永华,等.电动汽车充电负荷计算方法[J].电力系统自动化,2011,35（14）:36-42.Luo Zhuowei,Hu Zechun,Song Yonghua,et al.Study on plug-in electric vehicles charging load calculating[J].Automation of Electric Power Systems,2011,35（14）:36-42.

[15]余贻鑫,邱炜,刘若沁.基于启发式算法与遗传算法的配电网重构[J].电网技术,2001,25（11）:19-22.Yu Yixin,Qiu Wei,Liu Ruoqin.Distribution system reconfiguration based on heuristic algorithm and genetic algorithm[J].Power System Technology,2001,25（11）:19-22.

[16]Sun Yang,Zhang Lingbo,Gu Xingsheng.Membrane computing based particle swarm optimization algorithm and its application[C]//IEEE International Conference on Bio-Inspired Computing:Theories and Applications（BIC-TA）,2010:631-636.

[17]Zhang Yao,Huang Liang.A variant of P systems for optimization[J].Neurocomputing,2009,72（4-6）:1355-1360.

[18]Petr Sosik,Alfonso Rodriguez-Paton.Membrane computing and complexity theory:a characterization of PSPACE[J].Journal of Computer and System Sciences,2007,73（1）:137-152.

[19]Xiao JianHua,Zhang Xingyi,Xu Jin.A membrane evolutionary algorithm for DNA sequence design in

DNA computing[J].Chinese Science Bulletin,2012,57（6）:698-706.

[20]许立雄,吕林,刘俊勇.基于改进粒子群优化算法的配电网络重构[J].电力系统自动化,2006,30（7）:28-30.Xu Lixiong,Lü Lin,Liu Junyong.Modified particle swarm optimization for reconfiguration of distribution network[J].Automation of Electric Power Systems,2006,30（7）:28-30.

吴泓俭 男，1988年生，硕士，研究方向为含新能源的配电网重构和故障恢复及检修等。

E-mail:576910374@qq.com（通信作者）

雷 霞 女，1973年生，教授，硕士生导师，研究方向为电力市场、调度自动化、配电自动化等。

E-mail:274757067@qq.com

Membrane Computing Based Genetic Algorithm for Dynamic Reconfiguration of Distribution Network with Dividing Time and Considering Electric Vehicles and Wind Turbines

Wu Hongjian1,2Lei Xia1Liu Bin3Lu Yang1Xu Guiyang1
（1.Key Laboratory of Power Electronic Energy-Saving Technology Equipment Xihua University Chengdu 610039 China 2.Stage Grid Dazhou Power Supply Company Dazhou 635000 China 3.Nanping Power Bureau of Fujian Power Grid Corp.Nanping 353000 China）

AbstractDynamic reconfiguration with dividing time is becoming more and more important in the distribution network with more new energy.The dynamic reconfiguration model of distribution network with dividing time is established for electric power company,considering the costs of purchasing electricity from wind turbines,stochastic volatility,electric vehicle charging and discharging,and network loss.The final switch combination can be decided by minimum network cost with safe operation in each period.The model reflects the comprehensive effect of wind turbines and different kinds of electric vehicles on grid economy.Equal sections crossover probability selection method is used to overcome a large amount of duplicate solutions in the reconfiguration,and the improved algorithm based on the genetic membrane algorithm（GMA）is presented.The global searching capability of the algorithm is improved.Finally,the effectiveness and correctness of the proposed model and method are verified.

Keywords：Dynamic reconfiguration,wind turbine,different kinds of electric vehicle,equal sections crossover probability selection method,genetic membrane algorithm

作者简介

收稿日期2013-12-23 改稿日期 2014-06-06

中图分类号：TM731